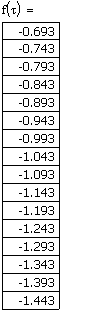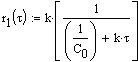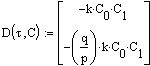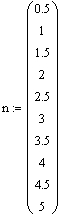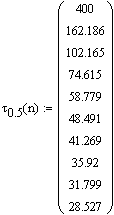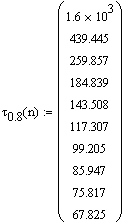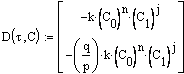Д.Г.НАРЫШКИН

                                                      КОНСПЕКТ ЛЕКЦИЙ

по курсу  «ХИМИЯ»

КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ

Возможности компьютерной математики

при исследовании поведения химических систем во времени

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТТУ)

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ                                                                                                                   3

1. ОБЩИЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКОЙ КИНЕТИКИ

1.1. Скорость реакции

1.2. Влияние концентрации на скорость реакции

1.3. Молекулярность и порядок реакции

1.4. Прямая и обратная задача химической кинетики

1.5. Реакция первого порядка

1.6. Реакции второго порядка

1.7. Реакции других порядков

1.8. Методы определения порядка реакции

2. Сложные реакции

2.1. Кинетика обратимых реакций

2.2 Параллельные реакции

2.3 Последовательные реакции

2.4 Метод квазистационарных концентраций

3. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ ХИМИЧЕСКИХ РЕАКЦИЙ

3.1.Уравнение Аррениуса

3.2. Связь энергии активации с тепловым эффектом реакции

3.3. Связь между скоростью реакции и равновесием

4. КИНЕТИКА ГЕТЕРОГЕННЫХ РЕАКЦИЙ

4.1. Общие понятия

4.2. Макрокинетика. Внешнедиффузионная область

4.3. Макрокинетика. Внутридиффузионное торможение

5. КИНЕТИКА РЕАКЦИЙ В ОТКРЫТЫХ СИСТЕМА

5.1. Химические реакторы.

5.2. Реакторы идеального смешения.

5.3. Реакторы идеального вытеснения.

5.4. Обратимые химические реакции в реакторах

 в реакторах смешения и вытеснения.

 6. Задачи

 7. Заключение  

 8. Рекомендуемая литература                                                                                     

ВВЕДЕНИЕ

        Термодинамический метод изучения химических реакций позволяет сделать вывод о принципиальной возможности исследуемого процесса в тех или иных условиях и о глубине его протекания.

     При постоянстве давления и температуры самопроизвольное протекание процесса возможно только в направлении уменьшения энергии Гиббса.

     Условие  определяет принципиальную возможность проведения процесса в заданных условиях из начального состояния в конечное, но не позволяет оценить скорость такого перехода.

      Это обстоятельство связано с тем, что  реакции не зависит от пути (механизма) процесса, а определяется только начальным и конечным состоянием системы.     

    Однако химические реакции могут протекать с самыми различными скоростями – от взрывных до очень медленных, протекающих в течение многих месяцев и лет. Даже одна и та же реакция, протекающая на различных катализаторах, может иметь скорости, различающиеся во много раз.

    В некоторых случаях необходимо увеличить скорость реакции, в других наоборот, уменьшить. Таких примеров можно привести множество.

    Поэтому изучение скорости протекания химических процессов (а это и составляет задачу кинетики) чрезвычайно важно.

    Для рационального проведения химических реакций необходимо уметь управлять ими, знать зависимости скорости от различных параметров.

По кинетике издано очень много учебной и методической литературы. Но все эти книги и учебные пособия написаны так, что хочется спросить: «Какое, милые, тысячелетье на дворе?»

     Современные системы компьютерной математики позволяют дать быстрый, и что, пожалуй, главное, наглядный  прогноз относительно поведения химической системы во времени.

     Однако в русскоязычной учебной литературе по кинетике химических реакций подход, в котором используются средства символьной математики  в совокупности со средствами решения  систем дифференциальных уравнений, представляемые математическим пакетом Mathcad, практически отсутствует.    

Поэтому, отвечая на естественный вопрос – чем предлагаемое учебное пособие отличается от множества других, можно ответить: настоящее пособие имеет цель продемонстрировать эффективность применения математического пакета Mathcad для решения задач химической кинетики.

   Специальные химические дисциплины, такие как термодинамика и кинетика, достаточно математизированы, и часто решение химической задачи вызывает у студентов значительные трудности, связанные с математикой – довольно часто это приводит к тому, что приходится сознательно упрощать задачу.

   Пособие иллюстрирует богатейшие возможности, которые открывает применение компьютерной математики перед исследователем для анализа поведения химических систем во времени.

    В этом отношении математические пакеты становятся практически незаменимыми элементами обучения, позволяющими сделать акцент на содержательном анализе полученных результатов.   

Знаком  >>>>>>  в тексте пособия отмечен переход к  Mathcad документу для интерактивного расчета.

1. ОБЩИЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКОЙ КИНЕТИКИ

                                1.1. Скорость реакции

Химическая кинетика – наука о скоростях и закономерно-стях  протекания химических процессов во времени.

   Химическая кинетика изучает механизм протекания процесса, т.е. те промежуточные стадии, состоящие из элементарных актов, через которые система переходит из начального состояния  в конечное.

    Химическая кинетика изучает скорости этих стадий и факторы, влияющие на их скорость.

    Уравнение химической реакции показывает начальное состояние системы (исходные вещества) и её конечное состояние (продукты реакции), но не отражает механизма процесса. Однако путь перехода системы из начального в конечное состояние может быть достаточно сложным и «извилистым».
    Так, например, реакция

протекает по следующему механизму:

первая стадия

вторая стадия

третья стадия

    Изучить кинетику реакции – значит показать, как реально протекает исследуемая реакция, её механизм, получить зависимость, связывающую скорость реакции с факторами, влияющими на неё.

    Различают два типа химических реакций: гомогенные и гетерогенные.

    К гомогенным относят реакции, у которых и исходные вещества и продукты реакции находятся в одной фазе. Взаимодействие веществ в таких реакциях происходит по всему объёму.

    К гетерогенным реакциям относят реакции, протекающие на границе раздела фаз.

    Пусть протекает реакция

(1.1)

где a₁, a₂, a_i, b₁, b₂, b_j – стехиометрические коэффициенты.

    Скорость реакции по i–му веществу в гомогенной системе определяется как количество i-го вещества, образующееся (или реагирующее) в единице реакционного объёма в единицу времени:

                          (1.2)

где V – объём реакционной зоны, N_i – количество i–го вещества.

    Если реакция протекает изохорически, т.е. объём во время реакции не меняется, то, поскольку концентрация и объём связаны соотношением

,

скорость реакции можно определить как изменение концентрации вещества во времени

  Ранее мы определили скорость химической реакции как изменение числа молей реагирующих веществ в единицу времени в единице объема, т. е.

где  — изменение числа молей одного из исходных веществ за время _.

   Таким образом определяется средняя скорость реакции для заданного интервала времени.

    Если объем в процессе реакции постоянен, то

где — изменение концентрации.

 Тогда

или 

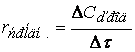
(скорость всегда положительна, а  может быть больше или меньше нуля в зависимости от того, изменение концентрации исходного вещества или продукта реакции мы рассматриваем).

    Если интервал времени , то мы получим истинную скорость реакции r в данный момент времени, т. е.

или

                        (1.3)

Размерность скорости: моль/(л·с).

   Не только знак, но и абсолютное значение скорости зависит от того, по какому из участников реакции она измерена.

   Так, например, при протекании реакции

скорость, с которой уменьшается концентрация водорода во время процесса, в три раза больше скорости убывания концентрации азота и в полтора раза выше скорости возрастания концентрации аммиака.

    Следовательно, для реакции

 скорости по компонентам реакции будут связаны соотношением:

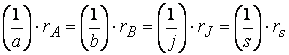
    Экспериментально установлено, что скорость реакции зависит от природы реагирующих  веществ, их концентрации (или давления), температуры, т.е.

     Раскрытие этой зависимости и составляет одну из задач кинетики.

1.2. Влияние концентрации на скорость реакции

Подход к выяснению зависимости скорости реакции от концентрации реагирующих веществ можно иллюстрировать следующим положением теории вероятностей: вероятность одновременного осуществления независимых событий равна произведению вероятностей каждого из них.

    Для того чтобы произошло химическое взаимодействие, например, реакция

A+B→продукты,

    необходимо, но не достаточно, столкновение реагирующих молекул А и В, т.е. одновременное нахождение их в определённой точке реакционного пространства.

    Вероятность ω нахождения молекулы для каждого из веществ прямо пропорциональна количеству молекул  в единице объёма, т.е. его концентрации:

, .

    Тогда вероятность того, что обе молекулы будут одновременно находиться в одной точке пространства, т.е. что они столкнутся, равна

Но не все столкновения приведут к реакции, а лишь их некоторая доля α, величина которой зависит от температуры и природы веществ, поэтому скорость реакции

A + B → продукты

равна

  или       

 Постоянную k, не зависящую от концентрации и зависящую только от температуры и природы реагирующих веществ, называют константой скорости реакции.

 Численное значение k выражает скорость реакции, когда концентрации реагирующих веществ равны 1 моль/л.

    Обобщим сказанное.

    Пусть протекает химическая реакция:

aA + bB + … → продукты.

    Тогда зависимость скорости реакции от концентрации можно выразить соотношением

           (1.4)

    Полученное выражение называют законом действия масс.

1.3. Молекулярность и порядок реакции

Число молекул, вступающих в реакцию, определяют молекулярность реакции.

    Так, если в реакцию вступает одна молекула, то такая реакция называется молекулярной реакцией. Если в реакции участвуют две молекулы (безразлично, одинаковые или нет), то такая реакция называется бимолекулярной. Встречаются также тримолекулярные реакции.

    Реакции более высокой степени молекулярности крайне редки из–за малой вероятности одновременного столкновения большого числа молекул.

    Поэтому большинство реакций протекают в несколько элементарных, простых стадий, в которых участвует небольшое число молекул.

     Так, например, рассмотренная выше реакция

протекает по следующему механизму:

первая стадия

вторая стадия (медленная)

третья стадия

     Определить такие стадии – значит определить механизм, или путь реакции.

    Скорость всей реакции определяется скоростью её наиболее медленной стадии, которая и определяет механизм.

    Поэтому закон действующих масс справедлив только для таких элементарных стадий.

    Молекулярность реакции легко определить в случае простых реакций, протекающих в одну стадию. В большинстве же случаев довольно трудно найти молекулярность реакции.

      Поэтому вводится понятие порядка реакции, который можно найти из кинетических уравнений, полученных экспериментально.

    Порядок реакции по данному веществу равен степени, в которой концентрация данного вещества входит в уравнение скорости реакции.

     Сумма показателей степеней, в которых концентрация всех исходных веществ входит  уравнение скорости реакции, равна порядку реакции в целом. Порядок химической реакции по веществу совпадает со стехиометрическим коэффициентом реакции  лишь в очень простых реакциях, например в реакции синтеза йодистого водорода:

                 H₂ + I₂ ® 2HI.

    Порядок этой  реакции по водороду (первый) и йоду (первый) равны стехиометрическими коэффициентами, а общий  порядок реакции (второй) равен сумме стехиометрических коэффициентов в уравнении скорости реакции

В подавляющем большинстве случаев порядок реакции по веществу отличается от стехиометрических коэффициентов уравнения реакции для этого вещества.

   Соответственно общий порядок реакции обычно не равен сумме стехиометрических коэффициентов уравнения реакции.

    Например, реакция

NO₂ + CO ® CO₂ + NO,

при температурах, меньших 298К, протекает по следующему механизму:

первая стадия процесса: NO₂ + NO₂ ® NO₃ + NO

вторая стадия процесса:  NO₃ + CO ® CO₂ + NO_2,

причем лимитирующей, т.е. скорость определяющей стадией является первая  стадия процесса:

NO₂ + NO₂ ® NO₃ + NO

   Тогда, согласно первому постулату химической кинетики, который утверждает, что скорость всей реакции равна скорости его самой медленной стадии, можно записать:

,

где- скорость первой стадии процесса.

   Согласно второму постулату химической кинетики, который утверждает, что скорость элементарной (одностадийной) реакции пропорциональна концентрации реагирующих веществ в степенях, равных стехиометрическим коэффициентам, получим зависимость скорости реакции           

NO₂ + CO ® CO₂ + NO

 от концентрации реагирующих веществ:            

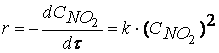
    Обратите внимание, что скорость реакции

NO₂ + CO ® CO₂ + NO

не зависит от концентрации оксида углерода CO.

   Уравнение, выражающее зависимость скорости реакции от концентрации каждого вещества, называют кинетическим уравнением реакции в дифференциальной форме.

    К сожалению, кинетическое уравнение реакции может быть получено только при её экспериментальном изучении и не может быть выведено из стехиометрического  уравнения.

1.4. Прямая и обратная задача химической кинетики

Определение на основании экспериментальных данных о зависимости концентраций от времени проведения процесса параметров кинетического уравнения – порядка реакции и значения константы скорости – составляет так называемую обратную задачу химической кинетики.

   Знание кинетического уравнения реакции в дифференциальной форме позволяет определить время достижения некоторой заданной концентрации реагирующего вещества (или продукта реакции).

   Пусть, например, протекает реакция           

aA + bB + … → продукты,   

кинетическое уравнение которой:

   Тогда время достижения некоторой концентрации вещества А можно определить, интегрируя кинетическое уравнение реакции в дифференциальной форме:

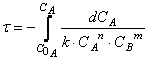
 Решая дифференциальное уравнение

 можно получить зависимость концентрации реагирующего вещества (или продукта реакции) от времени проведения процесса – так называемых кинетических кривых.

Определение – на основании феноменологической модели процесса – концентраций реагентов от времени проведения реакции составляет прямую задачу химической кинетики.

    Отметим сразу, что аналитически не всегда удаётся решить дифференциальное уравнение, особенно в случае сложной кинетики.

    В этом случае прибегают к численным методам решения и использование компьютерной математики. В частности, применение математических пакетов, например, таких, как Mathcad, становится незаменимым инструментом в исследовательской практике и в процессе обучения.

1.5. Реакция первого порядка

Реакция первого порядка может быть записана в общем виде:

                  аA®продукты

    Примером такой реакции может служить реакция разложения диметилового эфира:

CH₃OCH₃® CH₄ + H₂ + CO

    Кинетическое уравнение реакции первого порядка можно представить дифференциальным уравнением

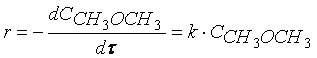           (1.5) 

    Тогда время t достижения некоторой концентрации диметилового эфира CH₃OCH₃  можно определить, интегрируя соотношение (1.5):

,

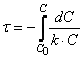где С и C₀ – концентрация CH₃OCH₃ в момент времени t и t=0.

      Интегрирование приводит к выражению

                        (1.6)           И тогда зависимость концентрации исходного вещества  CH₃OCH₃ от времени проведения процесса:

.     (1.7)

Из (1.7) следует, что концентрация исходного вещества со временем изменяется по экспоненциальному закону:

Проиллюстрируем изменение концентрации в зависимости от времени на примере реакции первого порядка

                      A ----> B  

с начальной концентрацией моль/л и константой скорости при некоторой температуре k=0.05 1/c

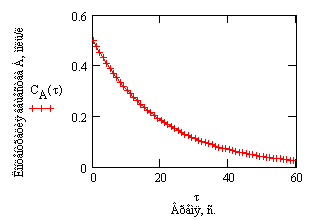
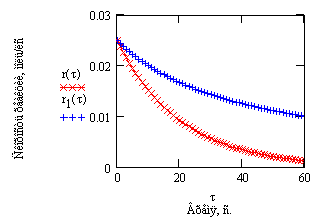
Рис.1. Зависимость концентрации

от времени в реакции первого порядка.

и, в логарифмических координатах, согласно зависимости

Рис.2. Зависимость логарифма концентрации

         исходного вещества от времени в реакции

         первого порядка.      

Поскольку

и скорость реакции по веществу А определяется как

,

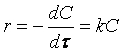то зависимость скорости реакции первого порядка можно выразить соотношением

,

иллюстрацией которого служит рис.3.

                     Рис.3.Зависимость скорости реакции первого

                     порядка от времени протекания процесса.

Здесь можно посмотреть Mathcad документ >>>>>>>>

Итак, если реакция протекает по первому порядку, то концентрация реагирующего вещества во времени меняется по уравнению (1.7)

             (1.7)            

   Графически в координатах (lnc, t) эта зависимость линейна с тангенсом угла наклона, равным tgά= – (рис.1.).

     Немного преобразовав (1.7)

получим

откуда

                     (1.9)

или                  

                     (1.10)

      Соотношение (1.10) позволяет определить время достижения некоторой заданной концентрации исходного вещества при протекании реакции первого порядка.

   Рассчитаем период  полупревращения (или полураспада) τ_1/2, т.е. время, необходимое для того, чтобы прореагировала половина исходного количества вещества.

    Подставляя C =(1/2)C₀  в  (1.9), получим

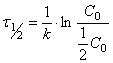
откуда

                        (1.11)

     Степень превращения  вводится соотношением

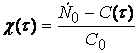                      (1.12)         где - исходная концентрация и С – концентрация в момент времени .

     Таким образом, степень превращения определяет долю исходного вещества, прореагировавшую к моменту времени .

     Естественно, что

    Тогда текущую концентрацию реагента в момент времени  можно выразить через степень превращения :

 и кинетическое уравнение реакции первого порядка

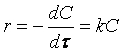
  можно выразить через степень превращения

   и

                     (1.13)

       Соотношение (1.13) позволяет определить время достижения некоторой заданной степени превращения исходного вещества при протекании реакции первого порядка

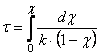                           (1.14)

       После интегрирования (1.13) получим:

                          (1.15)

    Степень превращения в зависимости от времени проведения процесса изменяется согласно

                          (1.16)

Особенностью реакции первого порядка является независимость периода полупревращения от концентрации реагента.

Обратная величина константы скорости реакции первого порядка имеет физический смысл средней продолжительности жизни отдельной молекулы.

Попробуйте доказать это положение.

Рассмотрим применение выведенных соотношений на конкретном примере.

Здесь можно посмотреть Mathcad документ >>>>>>>

     Реакция разложения глюкозы является реакцией первого порядка, и ее кинетическое уравнение в дифференциальной форме при 350К описывается соотношением:

Или через степень превращения

Кинетическое уравнение в интегральной форме

,                                                                            

где   - начальная концентрация исходного вещества.

      Или через степень превращения

 Из уравнения

можно определить время достижения некоторой заданной степени превращения:

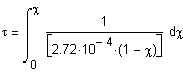(1.15)

Теперь, согласно уравнению

определим зависимость степени превращения от времени проведения реакции:                                

_(1.16)

Определим зависимость времени достижения степени  превращения   согласно (1.15), используя возможности, предоставляемые Mathcad.

Ввод степени превращения – исследуется  

зависимость времени достижения степени

                        превращения

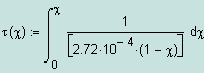     Ввод расчётной формулы.

Вывод результата счёта.

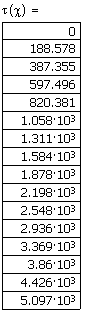
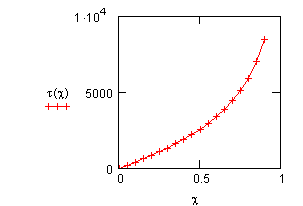
     Рис.4. Зависимость времени достижения заданной степени превращения глюкозы от степени превращения в реакции ее разложения при температуре 350К.

Определим зависимость степени превращения от времени проведения реакции согласно (1.16)

 _,

используя возможности, предоставляемые Mathcad.

Здесь можно посмотреть Mathcad документ >>>>

Ввод значения константы

             скорости реакции.

                Ввод временного интервала,        

                в течении которого будем

                исследовать изменение степени 

                                  превращения в зависимости от

                                   времени проведения процесса.

Ввод расчётной формулы

Вывод результат счёта.

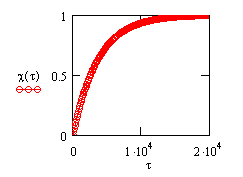
Рис.5. Зависимость степени превращения      

                          глюкозы от времени проведения процесса                                                                  

в реакции её разложения при 350К.

1.6. Реакции второго порядка

К таким реакциям относят реакции, скорость которых пропорциональна концентрации каждого из реагирующих веществ или квадрату концентрации одного из них.

    Рассмотрим вначале достаточно простой случай реакций вида

A + B → продукты,

тогда скорость такой реакции можно описать кинетическим уравнением 

            (1.17)

или, если C_A=C_B=С, то

                        (1.18)

    Пусть  и  – начальные концентрации вещества A и B и пусть C – концентрация веществ А в момент времени .

    Тогда

A  +  B → продукты

Начальная концентрация,    

моль/л      

Прореагировало к         -C -C

моменту

Концентрация              C

в момент

и уравнение (1.17) можно записать

                 (1.19)

 Или через степень превращения вещества А

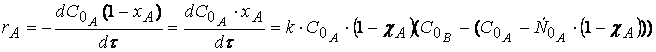
И после упрощений

           (1.20)  

   Если начальные концентрации веществ А и В равны, т.е., если , тогда (1.20) превращается в

                             (1.21)

      Сравнив кинетические уравнения первого

и второго порядка

,

вы, наверное, обратили внимание, что размерность константы скорости реакции зависит от порядка реакции. Размерность константы скорости реакции второго порядка .

    Найдем кинетическое уравнение  реакции второго порядка в интегральной форме, т.е. зависимость концентрации реагирующих веществ от времени протекания процесса.

    Если начальные концентрации реагирующих веществ реакции

A + B -à Продукты

равны, то, как мы показали

   Тогда

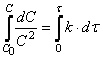
 И после интегрирования получим

                      (1.22)

или

  Соотношение (1.22) позволяет определить время достижения некоторой заданной концентрации исходного вещества при протекании реакции второго порядка – по-прежнему мы пока ограничиваемся случаем равенства начальных концентраций исходных веществ:

                         (1.23)

     И тогда время полупревращения для реакции второго порядка (подставляя C =(1/2)C₀ в 1.23))

                             (1.24)

и в отличие от реакции первого порядка зависит от начальной концентрации.

    Подставив в (1.22)

найдём зависимость степени превращения от времени протекания процесса:

                           (1.25)

    Напомним, что такой результат мы получим только в случае равенства начальных концентраций веществ А и В.

    Проиллюстрируем изменение концентрации в зависимости от времени на примере реакции второго порядка

             2A ------> B  

с начальной концентрацией =0.5моль/л и константой     скорости при некоторой температуре Т

Согласно (1.22) зависимость концентрации исходного вещества от времени проведения процесса определяется соотношением:

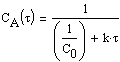
Нетрудно заметить, что в координатах «обратная концентрация- – время» зависимость линейна.

    Действительно, обозначим:

      Тогда  зависимость  обратной концентрации от  времени:

 и зависимость скорости реакции от времени

Иллюстрацией полученных зависимостей служат рис. 6-8.

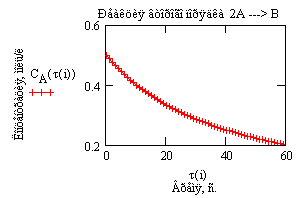
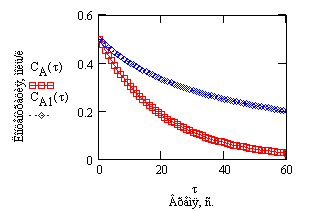
Рис. 6. Зависимость концентрации исходного вещества от времени проведения процесса

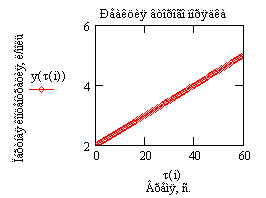
Рис.7. Зависимость обратной концентрации исходного вещества

   от времени проведения процесса

Рис.8. Зависимость скорости реакции  второго порядка от времени проведения процесса.

  Сравним ход зависимостей концентрации исходного вещества от времени проведения процесса для реакции первого и второго порядка, разумеется, при одинаковых значениях начальных концентраций и одинаковых числовых значениях констант скоростей.  

Соотношения, определяющие

зависимость концентрации

исходного вещества от времени

для реакции первого

и второго порядка    

Рис.9  Зависимость концентрации исходного вещества от времени проведения процесса.

 - реакция первого порядка

          A --->B

 - реакция второго порядка

          2A -->B

  Начальные концентрации исходных

веществ =0.5моль/л. Константы скорости   численно равны 0.05  

   Такой ход зависимостей концентрации от времени становится понятным после сравнения зависимостей скорости реакций от времени проведения процесса.

Соотношения, определяющие

зависимость концентрации

исходного вещества от времени

для реакции первого

и второго порядка

Рис.10. Зависимость скорости реакции от времени проведения процесса.

- реакция первого порядка

       A --->B

 - реакция второго порядка

         2A -->B

Начальные концентрации исходных

веществ =0.5моль/л. Константы скорости численно равны 0.05  

 Сравним теперь зависимости степени превращения от времени в реакции первого

 и второго

 порядка.  

Здесь можно посмотреть Mathcad документ >>>>>>>>>>>

Ввод константы скорости реакции и начальной концентрации:

Ввод временного интервала, в котором будет исследована зависимость                                                                                      

степени превращения от времени проведения процесса:

Расчётные соотношения, определяющие зависимость степени превращения в

реакции первого  и второго  порядка:

Вывод результата счёта.

Зависимость степени превращения от времени проведения процесса в реакции первого  и второго  порядка.

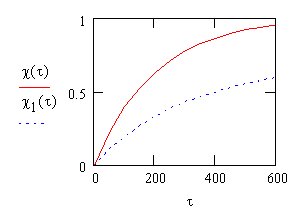
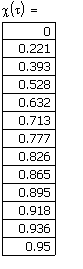
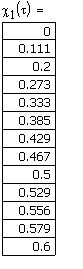
Рис.11.  Зависимость степени превращения от времени проведения процесса в реакции первого  и второго  порядка.

   Если начальные концентрации реагирующих веществ не равны, необходимо интегрировать уравнение (1.14)

             (1.14)

    Интегрирование (1.14) по частям или методом неопределённых коэффициентов  приводит к  выражению:

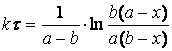                   (1.21)

    или

                    (1.22),

где ,  и x – число молей в 1л, которое прореагировало за время τ.

    Заметим попутно, что наличие современных компьютерных математических пакетов, например, таких, как Mathcad, практически устраняет трудности, возникающие при решении подобных задач.

   Проиллюстрируем это небольшим примером.

Как уже упоминалось, в случае неравенства начальных концентраций при протекании процесса   

A + B → продукты

кинетическое уравнение имеет вид (1.14)

и время, за которое прореагирует x молей, может быть рассчитано по соотношению

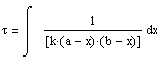
 Тогда с помощью символьного процессора Mathcad этот интеграл легко вычисляется.

  Для вычисления неопределенного интеграла от некоторого выражения, например, рассматриваемого

по определенной переменной (в нашем случае переменной является Х) выделяют в этом выражении переменную и выполняют команду Symbolcs/Variable/Integrate.

  После выполнения команды появляется вычисленное аналитическое представление неопределенного интеграла:

 Сравните это выражение с полученными ранее соотношениями (1.21) или (1.22)

  Расчеты, основанные на аналитическом интегрировании соотношения

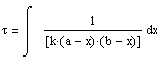
 представлены в  >>>>>>> Здесь можно посмотреть Mathcad документ

 Рассмотрим еще один подход к решению задач по определению зависимости концентрации реагирующих веществ от времени проведения процесса.  

   Рассмотрим реакцию омыления эфира в щелочном растворе                             >>>>> Здесь можно посмотреть Mathcad документ

   Исследуемая реакция является типичной реакций  второго порядка, а, значит, ее скорость описывается кинетическим уравнением (введя обозначения  и )

    При 298К константа скорости равна

    Пусть начальные концентрации равны  и

   Рассчитаем изменение концентраций реагирующих веществ в зависимости от времени протекания процесса.

Запишем кинетические уравнения:

Решим систему дифференциальных уравнений, т.е. найдем зависимость концентраций исходных веществ и продуктов реакции в зависимости от времени.

  Определим систему через формальную запись в Mathcad.

_,

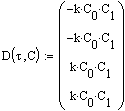  где , .

   Определим начальные условия

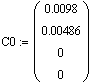
  Введем значение константы скорости исследуемой реакции

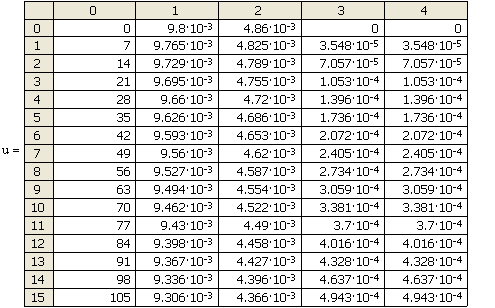
   Результаты решения (с помощью имеющейся в Mathcad встроенной функции, позволяющей решать систему  методом Рунге-Кутты с фиксированным шагом) представлены в матрице результатов и на рис.12.

 В левом столбце матрицы находятся значения аргумента ,деля-

щие интервал на равномерные шаги, в остальных столбцах - значения , , и .

В левом столбце матрицы находятся значения аргумента ,делящие интервал на равномерные шаги, в остальных столбцах - значения ,, и .                               

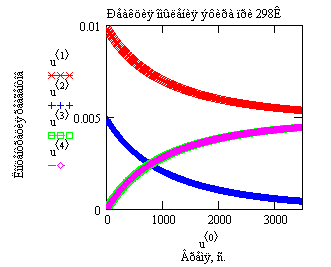
Рис.12. Зависимость концентрации реагирующих веществ от времени

- концентрация эфира,

- концентрация щелочи,

- концентрация спирта и

 - концентрация ацетат иона

в реакции омыления эфира                            при 298К.

Начальные концентрации эфира  и щелочи

Здесь можно посмотреть Mathcad документ >>>>>>>>>>>

  Период полупревращения для реакции второго порядка найдем из (1.20)

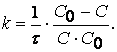
 Подставив C = ½ C₀, получим

  Откуда время полупревращения для реакции второго порядка в случае равенства начальных концентраций веществ А и В

                       (1.23) 

Для реакции второго порядка время полураспада обратно пропорционально начальной концентрации исходного  вещества.

    Рассмотрим общий случай реакции второго порядка:

                    pA  +  qB ------>   ПРОДУКТЫ,

причём

                    pA  + qB  ------>   ПРОДУКТЫ,

Исходная концентрация,

 моль/л      

Концентрация в

момент

     Поскольку для реакции

         aA + bB + ......> cC + dD + ...

скорости, измеренные по компонентам реакции равны

 ,

то для рассматриваемого процесса

           pA  +  qB ------>   ПРОДУКТЫ

и

    Тогда система кинетических уравнений в дифференциальной форме:

,

решение которой даёт возможность исследовать изменение концентраций реагирующих веществ в зависимости от времени протекания процесса.

     Для решения воспользуемся возможностями, которые предоставляет математический пакет Mathcad.

     Для формальной записи в Mathcad. введём обозначения:

 концентрация вещества  ,

Ввод стехиометрических

коэффициентов                                             

Ввод начальных концентраций

реагентов.

Ввод числа шагов, на которых численный метод находит решение.

Ввод системы кинетических уравнений в дифференциальной форме.

Ввод начальных концентраций.

Ввод значения константы

скорости реакции.

Вывод решения - здесь:

 -  время,

 - концентрация вещества А 

 - концентрация вещества B 

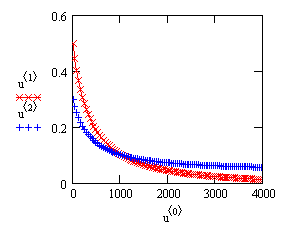
Рис.13. Зависимость концентраций исходных веществ от времени протекания процесса в реакции pA  +  qB ------>   ПРОДУКТЫ - время,  - концентрация вещества А   и  - концентрация вещества B

 Исследуем теперь зависимость степени превращения исходных веществ от времени протекания процесса

             pA  +  qB ------>   ПРОДУКТЫ

     Поскольку  текущие концентрации связаны со степенью превращения

и

,

кинетические уравнения можно представить:

Для формальной записи в Mathcad системы дифференциальных уравнений введём обозначения:

степень превращения  вещества  A  ,

Решим систему дифференциальных уравнений и тем самым найдём зависимость степени превращения исходных веществ от времени протекания процесса

             pA  +  qB ------>   ПРОДУКТЫ  

                                                                                                  Ввод стехиометрических коэффициентов.

                                                             Ввод начальных концентраций реагентов.

                  Ввод системы кинетических уравнений в дифференциальной форме

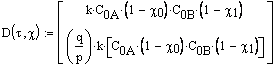
                                                            Ввод начальных степеней превращения.

                                 Ввод числа шагов, на которых численный метод находит решение. 

                                                               Ввод значения константы скорости реакции.

 Вывод решения - здесь:

 -  время,

 - степень превращения вещества А 

 - степень превращения вещества B 

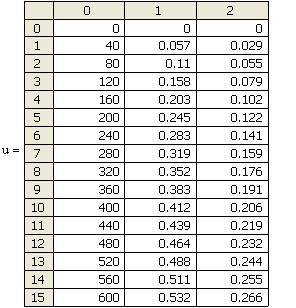
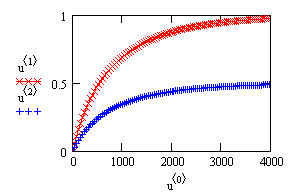
Рис. 14.  Зависимость степени превращения исходных веществ от времени проведения процесса

             pA  +  qB ------>   ПРОДУКТЫ

 -  время,    - степень превращения вещества А  ;    - степень превращения  вещества B 

     Определим теперь время достижения некоторой степени превращения  исходного вещества A при протекании реакции

pA  +  qB ------>   ПРОДУКТЫ

Кинетическое уравнение реакции

   Интегрируя кинетическое уравнение, найдём соотношение, определяющее связь между степенью превращения и временем её достижения:

Ввод стехиометрических коэффициентов.

 Ввод значения константы

 скорости реакции.

Ввод начальных  концентраций          реагентов.

  Ввод соотношения, определяющего   интервал степени превращения . Степень превращения изменяется от 0 до =0.95 с шагом 0.05

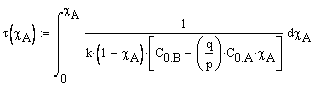
Ввод соотношения, определяющего           связь между степенью превращения и временем её достижения.

Вывод результата - время достижения некоторой степени превращения

Вывод результата - время достижения степени превращения

_{Разумеется, вы можете вывести результат и при другом значении степени превращения.}

Рис. 15. Зависимость времени достижения степени превращения   при проведении процесса

              pA  +  qB ------>   ПРОДУКТЫ

То, что соотношение между начальными концентрациями влияет на степень превращения, следует из анализа кинетического уравнения реакции. Однако степень влияния можно установить только в результате расчёта.

     Исследуем влияние соотношения начальных концентраций на время достижения некоторой заданной степени превращения при протекании реакции

pA  +  qB ------>   ПРОДУКТЫ

  Соотношение, определяющее связь между степенью превращения вещества A и временем её достижения:

Ввод стехиометрических коэффициентов.

Ввод начальной концентрации вещества A.

Ввод константы  скорости реакции.

  Ввод степени превращения

   Ввод соотношения, определяющего связь между временем достижения степени превращения c и соотношением начальных концентраций  .

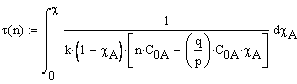
Вывод результата: время достижения степени превращения c = 0.5 при соотношением начальных концентраций  

Вывод результата - время достижения некоторой степени превращения c = 0.5 и c = 0.8 при изменении соотношения начальных концентраций    от   n = 0.5  до n = 5.

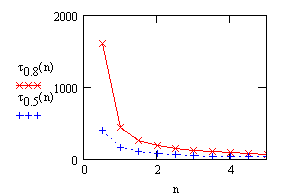
Рис. 16. Влияние соотношения начальных  концентраций  на время достижения некоторой заданной степени превращения при протекании реакции

                   pA  +  qB ------>   ПРОДУКТЫ 

1.7. Реакции других порядков

Реакции третьего порядка встречаются достаточно редко, поэтому мы не будем их рассматривать подробно.

Отметим только, что для реакции третьего порядка

A + B + C → продукты

кинетическое уравнение имеет вид

    Некоторые реакции, осложнённые адсорбционными стадиями, имеют дробный порядок

,

где  α < 1.

    Задачу определения зависимости концентраций реагирующих веществ от времени протекания процесса рассмотрим для наиболее общего случая на примере  реакции

                                         pA  +  qB ------>   ПРОДУКТЫ,

причём    и порядок реакции по веществу   A равен  n и по веществу  B  равен  j,  т.е. скорость реакции описывается кинетическими уравнениями:

Поскольку для реакции

                                        aA + bB + ......> cC + dD + ...

скорости, измеренные по компонентам реакции равны

 ,

то для рассматриваемого процесса

                                          pA  +  qB ------>   ПРОДУКТЫ

и

Тогда система кинетических уравнений в дифференциальной форме:

Задача сводится к решению системы этих дифференциальных уравнений.

   Решение системы даёт возможность исследовать изменение концентраций реагирующих веществ в зависимости от времени протекания процесса.

      Конечно, можно проинтегрировать соотношение

,

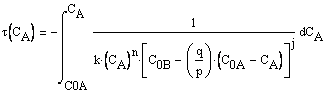хотя во многих случаях это и сопряжено со значительными трудностями.

(Чтобы убедиться в этом, попробуйте проинтегрировать самостоятельно и потом из полученного выражения "вытащить" зависимость концентрации от времени проведения процесса )  

       Однако, мы "пойдём другим путём" и для решения системы

воспользуемся возможностями, которые предоставляет математический пакет Mathcad.

         Введём обозначения для формальной записи в  Mathcad:

 концентрация вещества ,

Ввод порядка реакции.

Ввод стехиометрических коэффициентов.

Ввод значения константы скорости реакции.

Ввод системы кинетических

 уравнений в дифференциальной форме.

  Ввод начальных концентраций  реагентов.

Ввод числа шагов, на которых численный метод находит решение.

    Ввод встроенной функции

 для решения системы дифференциальных уравнений.

 - вектор начальных значений в точке , - конечная точка расчёта.

   В рассматриваемом случае решение находим на интервале 0 - 2500с.

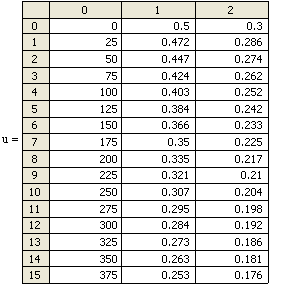
Вывод решения - здесь:

 -  время, c.,

 - концентрация вещества А

 - концентрация вещества B

Концентрации при других значениях времени можно посмотреть с помощью полосы прокрутки.

       Графическая иллюстрация полученных результатов приведена на рис.17.

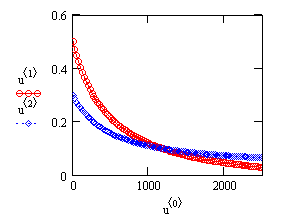
Рис. 17. Зависимость концентраций исходных веществ от времени протекания процесса в реакции

                2A + B ------> ПРОДУКТЫ

скорость которой описывается кинетическим уравнением , константа скорости , порядки реакции по веществам  , _;  -  время,  - концентрация вещества А   и    - концентрация вещества B 

Здесь можно поработать с Mathcad документом >>>>>>>>>>