Решение уравнения линейной заменой сводится к решению неполного уравнения

.

Решение неполного уравнения будем искать в виде , где . Подставим это выражение в многочлен третьей степени:

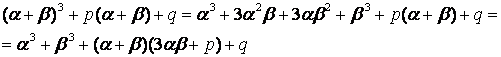
и зададим дополнительное условие на и :

.

В результате мы получим систему

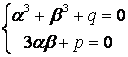, (1)

которая обладает тем свойством, что если пара чисел является ее решением, то является решением неполного уравнения. Верно и обратное: если является корнем неполного уравнения, то найдется такая пара чисел , что и удовлетворяют системе (1).

Преобразуем второе уравнение так, чтобы в нем фигурировали третьи степени и :

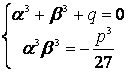. (2)

У этой системы есть посторонние корни по сравнению с системой (1) и мы должны будем оставить только те и , которые удовлетворяют условию

.

Введем обозначения и перепишем нашу систему с новыми неизвестными:

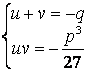(3)

Решение этой системы сводится к решению квадратного уравнения относительно :

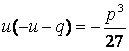
или

.

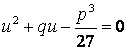Находим дискриминант:

.

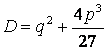Корни квадратного уравнения:

,

.

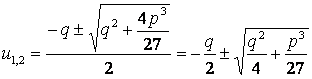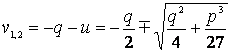В виду симметричности рассматриваемых систем, симметричности формул для и , и поскольку нас интересуют не сами решения системы (1), а суммы чисел, составляющих пары, оставим только одно из двух решений системы (3):

,

.

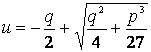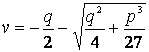Вернемся к решению системы (2).

,

.

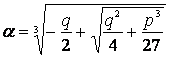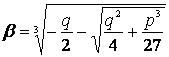Теперь для того чтобы решить систему (1), т.е. соблюсти условие , можно поступить следующим образом. Пусть - любое значение корня третьей степени, вычисляемое по формуле для , а . Положим

,

и соответственно

,

.

Теперь легко заметить, что пары и , имеющие одинаковые индексы, и только они удовлетворяют условию .

Итак, система (1) имеет три (с точностью до симметрии в парах) решения. Мы получили три корня неполного уравнения:

, и .

Условно решение неполного кубического уравнения можно записать в виде формулы (формула Кардано):

.
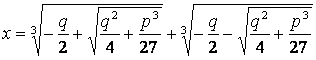