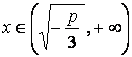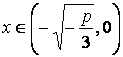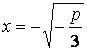Исследование многочлена третьей степени с помощью производной

Для решения вопроса о количестве действительных корней уравнения рассмотрим функцию , заданную на промежутке . непрерывно дифференцируема во всей области определения. Заметим, что . Найдем производную функции :

.

Легко видеть, что .

Нетрудно показать, что график функции центрально симметричен – центром симметрии является точка .

Если , то функция не убывает на промежутке и поэтому уравнение имеет единственный действительный корень, так как . Если , то корень отрицательный, если , то корень положительный, и, наконец, если , то корнем является .

Рассмотрим случай, когда . Уравнение имеет два корня:

,

.

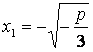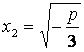Так как вторая производная, , имеет тот же знак, что и , отрицательному корню соответствует точка локального максимума функции , положительному – точка локального минимума. При функция монотонно возрастает. При функция монотонно убывает. Наконец при функция снова монотонно возрастает.

Найдем значения функции и :

,

.

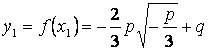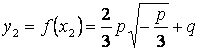Нетрудно видеть, что при любых значение функции в левой точке локального экстремума больше значения функции в нуле, а то, в свою очередь, больше значения функции в правой точке локального экстремума:

.

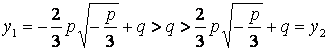Введем обозначение .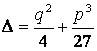

Если , а , то меньше нуля. В таком случае по теореме о промежуточных значениях непрерывной функции функция имеет три нуля: на интервале , на интервале и на интервале .

Если и , а , то больше нуля. В таком случае функция меняет знак только однажды и по теореме о промежуточных значениях непрерывной функции уравнение имеет единственный действительный корень – на интервале .

Если же , а , то равно нулю. В таком случае уравнение имеет два действительных корня: по теореме о промежуточных значениях непрерывной функции один из них лежит на полуинтервале и один найден явно, а именно, .

Аналогично, если , а , то больше нуля, и уравнение имеет три действительных корня: на интервале , на интервале и на интервале .

Если , а , то меньше нуля, и уравнение имеет единственный действительный корень – на интервале .

Если , а , то равно нулю и уравнение имеет два корня: один корень , другой принадлежит интервалу .

В Таблице приведены данные о количестве действительных корней уравнения и их кратностях при различных и . (Крастностью корня многочлена называется степень одночлена , с которой он входит в разложение данного многочлена.)

p	q,		корни
			Один отрицательный однократный
			, однократный
			Один положительный однократный
			Один отрицательный однократный
			, трехкратный
			Один положительный однократный
			Один, однократный,
			Два: двукратный и однократный
			Три: , ,
			Три: , и
			Три: , и
			Два: двукратный и однократный
			Один однократный
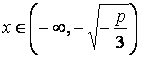
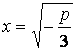
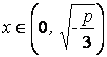