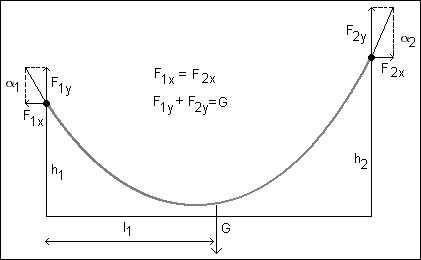
Некоторые особенности решения систем нелинейных алгебраических уравнений в среде Mathcad

(Индивидуальное расчетное задание по курсу «Информатика»)

В.Очков

Рассмотрим эти особенности на примере задачи о провисании цепи.

Имеется цепь (однородная, гибкая, нерастяжимая, тяжелая нить) фиксированной длинны S подвешенная на двух «столбах» высотою h1 и h2, отстоящих друг от друга на расстоянии L (пролет) – см. рис. 1. Необходимо определить величину h – минимальное расстояние («зазор») цепи от земли и величину х0 – "отстояние" этого зазора от первого столба, на котором у нас будет зафиксирована ось y. Ось х «лежит на земле».

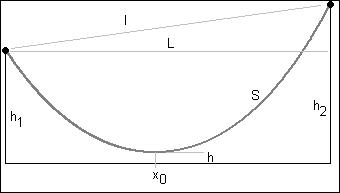
Рис. 1. Схема задачи о провисании цепи

Если принять, что оси декартового графика, отображающего формулу цепной линии, пересекаются в самой нижней точке, то формула цепной линии будет имеет такой общий вид a·(cosh(x/a)-1). Эта формула выводится в процессе решения дифференциального уравнения, составленного после анализа баланса сил, действующего на бесконечно малый элемент цепи. Процесс составления и ход решения этого дифференциального уравнения можно, например, увидеть на сайте http://www.exponenta.ru/educat/class/test/hyperb/10.asp.

Если мы будем применять формулу цепной линии к нашей задаче (см. рис. 1), где оси декартового графика пересекаются не в нижней точке цепи, а у основания левого столба и тем самым сдвинуты на величины x0 (по горизонтали) и h (по вертикали), то формула цепной линии примет вид h + a·(cosh((x0 – x)/a)-1). С этой формулой мы и будем дальше работать.

Наша задача о провисании цепи будет сводиться к поиску значений констант х0, h и а, входящих в формулу цепной линии. Для решения этой задачи нужно составить систему трех нелинейных алгебраических уравнений с вышеперечисленными тремя неизвестными. Первые два уравнения получаются при рассмотрении двух точек закрепления цепи на столбах: (0; h1) – левый столб и (L; h2) – правый столб. Третье уравнение возникает при вводе в задачу формулы, описывающей длину дуги линии. Вывод этой формулы можно увидеть на сайте http://mathserfer.com/theory/kiselev2/node43.html, например.

Любую задачу в среде математического пакета следует начинать решать аналитическими (символьными) методами. В нашем случае следует попытаться вывести общие формулы для нахождения неизвестных х0, h и а в задаче о провисании цепи. Но попытки аналитического решения нашей системы алгебраических уравнений были неудачными[1] – см. рис. 2.

 

Рис. 2. Попытки аналитического решения системы алгебраических уравнений

Поэтому мы будем решать полученную систему трех нелинейных алгебраических уравнений численными методами – см. рис. 3.

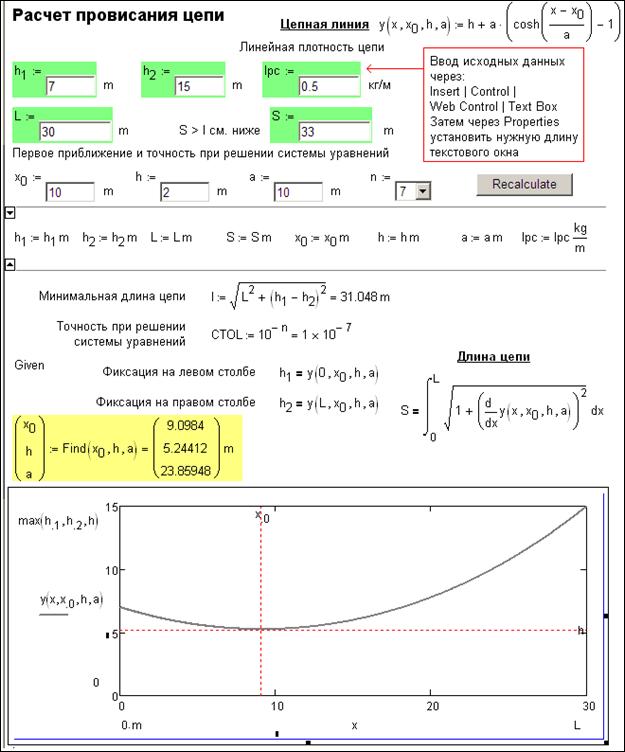
Рис. 3. Решения задачи о провисании цепи численными методами

Численные решения системы нелинейных алгебраических уравнений в среде Mathcad требует задания первого приближения к искомым величинам, а также значения точности при решении, хранимой в системной переменной CTOL. Пользователь расчета, показанного на рис. 3 задает не только значения исходных данных по геометрии цепи (h1, h2, L и S), но и значения первых приближений для неизвестных х0, h и a. Первое приближение для неизвестных х0 и h подобрать несложно. Значение х0 будет равно значению L/2, если h1 = h2 (симметричная цепь, подвешенная на двух одинаковых столбах). Значение х0 будет сдвигаться к нулю (к левому столбу), если h1 < h2, или к значению L (к правому столбу), если h1 > h2. Но при h1 ≠ h2 и при особом натяжении цепи точка минимального провисания может находиться вне отрезка 0 – L. О силах натяжения цепи мы поговорим позже. Сейчас же мы отметим, что в нашей задаче вычисляется значение l (эль) – минимальная длина цепи, которую возможно натянуть между нашими столбами. При h1 ≠ h2 и при S (длина цепи), стремящейся к l, точка минимального провисания цепи будет смещаться к одному из столбов и даже выходить из заданного диапазона 0 – L. Это нужно учитывать при задании значений первого приближения для переменных х0 и h. Значения первого приближения неизвестного а интуитивно определить сложнее. Значение а должно быть больше нуля, иначе цепь будет провисать не вниз, а… вверх и примет вид… арки. О такой арке мы поговорим позже. Сейчас же только отметим, что наша система уравнений имеет как минимум два решения – провисающая цепь и арка. Выбор первого приближения для переменной a определяет, какое из решений (провисающая цепь или арка) будет найдено. На ход решения и на его результат влияет значение системной переменной CTOL, значение которой (10-3, 10-7, 10-10 или 10-15) также задается пользователем через задание значений переменной n. Рекомендуется сначала снизить точность решения (CTOL:= 10-3), а потом повышать его до 10-7, 10-10, или даже до 10-15, одновременно перенося ответ в первое приближение. Так приходится поступать, если необходимо провести новый расчет с исходными данными, существенно отличающимися от тех, какие показаны на рис. 3/

Функция Find возвращает значения своих переменных, превращающих наши три уравнения в тождества, вернее, в «приближенные» тождества: правые и левые части уравнений после подстановки в них найденных функцией Find значений переменных h, х0 и a должны отличаться друг от друга на величину, не превышающую по модулю значение, хранимое в переменной CTOL. Все это определяет особый характер работы с расчетом, показанным на рис. 3. Повторяем, если пользователь захочет изменить исходные данные и посчитать провисание цепи при новых начальных условиях, то решение иногда может быть не выдано, вернее, будут выданы не числа, а сообщение об ошибке. Тут нужно будет вернуться к прежним исходным данным и менять их не все сразу, а поочередно и постепенно, перенося ответ, который будет выдавать функции Find, в первое приближение, и изменяя значение переменной CTOL .Все это определяет некую интерактивность расчета, показанного на рис. 3: пользователь не просто вводит новые исходные данные и получает ответ, а помогает компьютеру найти ответ, меняя параметры численного решения системы уравнений. Подробнее об этой особенности численного решения задач можно прочесть в статье «Решение алгебраических уравнений и систем или Ван Гог в среде Mathcad» http://twt.mpei.ac.ru/ochkov/Carpet/index.htm.

В исходных данных можно видеть величину линейной плотности цепи. Это позволяет при решении задачи также оценить и силы натяжения цепи на ее концах при заданном ускорении свободного падения (g – встроенная в Mathcad константа). На рис. 4 показана скрытая область расчета, в котором определяются силы, действующие на цепь в двух точках ее крепления F1 и F2 с разложением этой силы по осям x и y (Fx1 Fy1 и Fx2 Fy2).

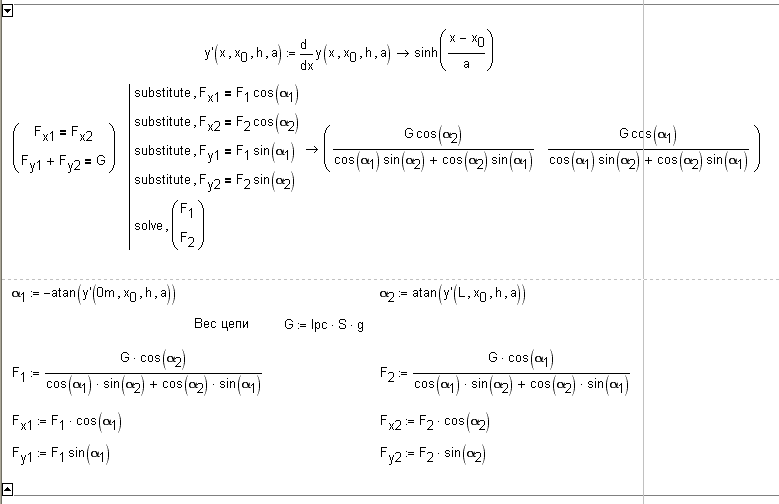
Рис. 4. Расчет сил, действующих на цепь в местах крепления к столбам

Для расчета этих сил сначала определяются углы крепления цепи к столбам α1 и α2 – см. рис. 5. Это сделать несложно, если известны параметры цепной линии х0, n и а: берется первая производная от формулы цепной линии и учитывается, что геометрический смысл производной – это тангенс наклона касательной.

Рис. 5. Силы, действующие на цепь в местах ее крепления

Если известны углы наклона крепления цепи у столбов, то можно определить силы, растягивающие цепь в этих местах. Для этого составляется и решается система двух уравнений, включающая в себя баланс проекций сил (F) действующих на цепь по горизонтали (Fx) и вертикали (Fy). Решение этой задачи показано на рис. 4 и 6.

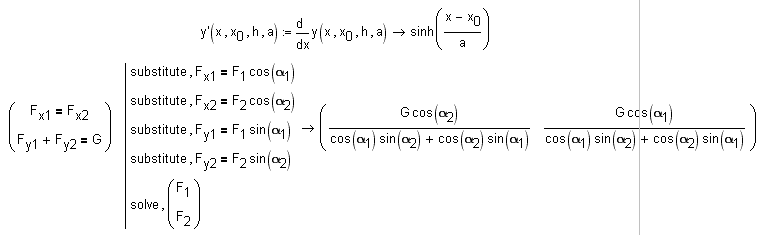
Рис. 6. Вывод формул для расчета сил, действующих на цепь в местах ее крепления

При этом силу разрыва цепи как функцию от х можно определить так - см. рис. 7

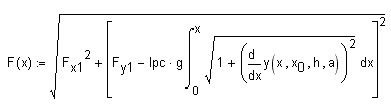
Рис. 7. Вывод формул для расчета силы разрыва цепи как функцию от х

 

Задания, составляющие суть расчетное задание по курсу «Информатика» на 2-м семестре:

  1. Изменить расчет провисания цепи (рис. 3) так, чтобы исходной величиной была не длина цепи S, а величина h – минимальное расстояние («зазор») цепи от земли. Определить при этом длину цепи S.
  2. Вставить в задачу операторы (рис. 4), позволяющие рассчитать силы натяжения (разрыва) цепи у мест крепления на столбах.
  3. Убрать из расчета (рис. 3) исходную величину lpc (линейная плотность цепи). И вместо нее ввести новые исходные величины: диаметр провода (d), плотность материала провода (ρ) и предел прочности (δ) материала провода. Допустив, что такой провод – это наша однородная, гибкая, нерастяжимая, тяжелая нить (цепь), ввести в расчет проверку на прочность натянутого между столбами провода. Параметры выбранного провода (стального, медного, алюминиевого, нейлонового и т.д. – выбор за конкретным студентом) найти в Интернете.
  4. Развить задачу, описанную в п.3 – сделать попытки определения максимального расстояния между столбами, при котором можно повесить провод из выбранного материала, так, чтобы он не оборвался. При этом можно менять диаметр провода и его длину.
  5. Смоделировать провисание провода с некоторым запасом прочности (см. п. 3). Далее смоделировать обледенение провода и определить толщину льда на проводе, при которой он оборвется.
  6. Построить график изменения силы натяжения цепи/провода по его длине (или по оси x - см. рис. 7)
  7. Составить уравнение момента сил относительно начала координат и определить величину l1, отмечающую на рис 5 точку приложения веса цепи.
  8. Создать анимации процессов натяжения цепи (см. образцы >>> и >>>)

Подсказка к решению - см. http://communities.ptc.com/message/162401

 

Послесловие 1

Расчет провисания цепи выложен на сайте http://twt.mpei.ac.ru/MCS/Worksheets/chain.xmcd.

Как известно, теория должна проверяться практикой. На график провисания цепи можно повесить реальную цепь и убедиться, что она точно накрывает линию на графике:

 

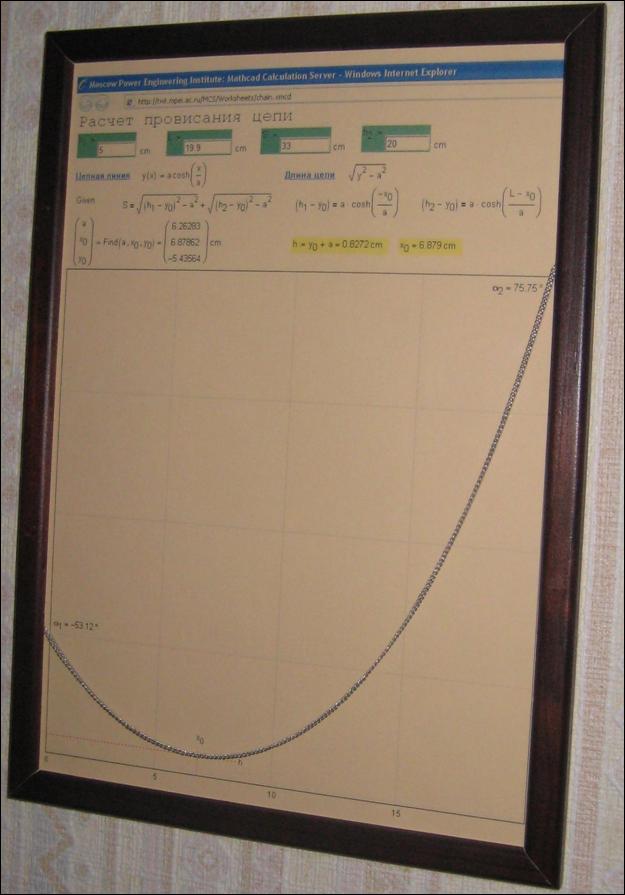
Рис. 7. Реальная цепь на реальной картине цепи

Получается довольно-таки интересный математический сувенир!

 

Рис. 7а. 6 апреля 2012 года в г. Кэмбридж (США) автор статьи подарил этот математический "сувенир" Алену Раздоу (Allen Razdow) - создателю Mathcad.

Цепь провисает под действием силы тяжести. Но величины g (ускорение свободного падения) в формуле цепной линии нет. Это означает, что любая цепь одинаково провисает и на Земле и на … Луне. А на Земле тяжелая стальная цепь и тонкая нитка будут провисать совершенно одинаково. Главное, чтобы они были «однородные, гибкие и нерастяжимые» (тут можно говорить о некой математической провисающей цепи). Ускорение свободного падения присутствует в формуле, по которой определяют период качания маятника. Если на нашей цепи подвесить тяжелый груз, то такой маятник по-разному будет качаться на Земле и на Луне. Задача маятника, решаемая с помощью Mathcad, выложена здесь http://twt.mpei.ac.ru/ochkov/Pendulum/index.html.

Тут можно вспомнить, что пушинка и тяжелый камень будут падать на землю одинаково, если… это будет происходить в вакууме. В задаче о провисании цепи есть также одно «если», но оно более тонкое: две цепи одинаковой длины и одинаково закрепленные будут одинаково провисать на Земле и на Луне, если не учитывать разную конфигурацию гравитационного поля на Земле и на Луне. Представим себе, что сквозь центр Земли проделан тоннель, и мы туда не бросаем камень (любимый гипотетический эксперимент физиков), а плавно опускаемся вниз на лифте, в котором подвешена наша цепь. Как тут будет меняться ее форма?!

 

Послесловие 2

В художественной литературе нередко можно видеть математические задачи. Некоторые из них сводятся к решению систем алгебраических уравнений линейных и нелинейных. Вот три такие задачи, по которым также можно отметить некоторые особенности решения систем алгебраических уравнений в среде Mathcad.

Рассказ А.П. Чехова «Репетитор» начинается с такого диалога:

— Теперь по арифметике... Берите доску. Какая следующая задача?

Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует:

— "Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?" Повторите задачу.

Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.

— Для чего же вы это делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю!

Зиберов делит, получает 3 с остатком и быстро стирает.

"Странно... — думает он, ероша волосы и краснея. — Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая..."

Учитель глядит в ответы и видит 75 и 63.

"Гм!.. странно... Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то".

— Решайте же! — говорит он Пете.

— Ну, чего думаешь? Задача-то ведь пустяковая! — говорит Удодов Пете. — Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич.

Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет.

— Это задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил... понимаете? Теперь, вот, надо вычесть... понимаете? Или, вот что... Решите мне эту задачу сами к завтраму... Подумайте...

Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол.

— И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и вздыхая. — Вот извольте видеть...

Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.

— Вот-с... по-нашему, по-неученому.

Такую систему двух алгебраических уравнений с двумя неизвестными («Это задача, собственно говоря, алгебраическая <…> Ее с иксом и игреком решить можно»): x + y = 138 и 5 x+3 y = 540 можно решить без компьютера и даже без калькулятора, выполнив несложные арифметические действия, что и отмечено у Чехова. На счетах это сейчас, конечно, мало кто сделает. Мы эту задачу сейчас решим на компьютере (на современных «счетах»), воспользовавшись «компьютерными счетами» – программой Mathcad – см. рис. 1.

Рис. 1. Решение задачи Удодова в среде Mathcad

Программа Mathcad, как известно, работает не просто с величинами, а с физическими величинами (длина, масса, и т.д.): в программу Mathcad вшиты единицы измерения: (метры, килограммы и т.д.). Но аршина как и многих других устаревших (национальных) единиц измерения в пакете Mathcad нет. Тут можно вспомнить (или найти в Интернете) информацию о том, что аршин равняется трети сажени, которая в свою очередь равна семи футам («семь футов под килем!»). Английский же фут обозначение (ft) встроен в Mathcad – см. первый оператор присвоения (:=) на рис. 1, с помощью которого в расчет вводится пользовательская единица длины – арш (аршин – семь третей фута). Второй оператор присваивания := вводит в расчет пользовательскую единицу стоимости руб, связывая ее с встроенной «нейтральной» (не $, € и т.д.) единицей стоимости – ¤. Можно отметить, что задачу Удодова (так мы ее условно назовем), как и многие другие подобные задачи, можно решить и без привлечения единиц измерения (так, например, будет решена вторая задача). Но единицы измерения, во-первых, повышают наглядность задачи, уровень ее документирования и, во-вторых и в главных, снижают риск ошибки в решении, когда, например, аршины пытаются сложить с рублями.

Задачу Удодова можно, конечно, решить, используя блок Given-Find. Но задача Удодова сводится не просто к решению системы алгебраических уравнений, а к решению системы линейных алгебраических уравнений. Для решения этой специфической задачи в среде Mathcad есть специальные инструменты.

На рис. 1 показано, как задача Удодова решается в среде Mathcad с использованием операторов работы с векторами и матрицами. Для этого в расчет вводится и заполняется квадратная матрица М, хранящая коэффициенты при неизвестных системы уравнений, и вектор v – вектор свободных членов (правых частей) системы уравнений. Решение задачи (63 аршина синего сукна и 75 аршин черного сукна) находится через векторное умножение инвертированной (обратной) матрицы М-1 на вектор v. Кстати, в рассказ Чехова вкралась неточность. У Удодова после «щелканья костяшками на счетах» должно получиться 63 и 75 аршин сукна, а не 75 и 63 аршин (см. цитату выше). Ведь, в условии задачи сначала называется цена синего сукна, а потом – черного («синее стоило 5 руб. за аршин, а черное 3 руб.»). Отсюда по логике вещей число 75 (икс) должно относиться к синему сукну, а число 63 (игрек) – к черному. А это на самом деле не так: х = 63, а y = 75.

На рис. 1 показано решение задачи Удодова в версии пакета Mathcad, где возможна запись в массивах (векторах и матрицах) величин с разной размерностью. Но в обычных версиях Mathcad и в Mathcad-подобной программе SMath (www.smath.info) массивы могут хранить величины одной размерности или вовсе безразмерные. Из-за этого задачу Удодова в этих средах следует решать без использования единиц измерения – см. рис. 2.

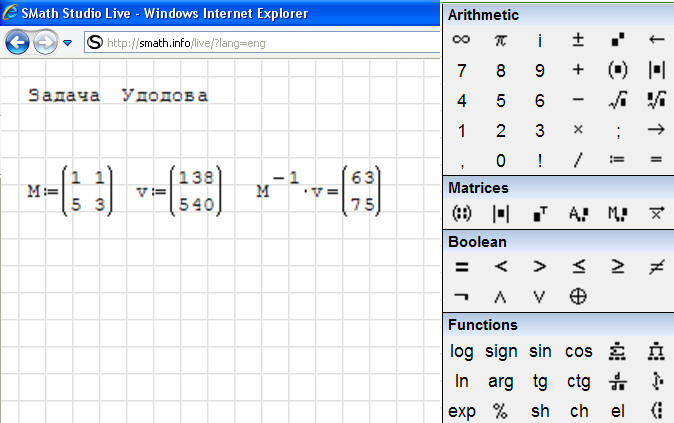
Рис. 2. Решение задачи Удодова в среде программы SMath.

В задаче Удодова число уравнений (2) равно числу неизвестных (2). Но в жизни и, соответственно, в литературе так бывает далеко не всегда. Два последующих примера тому иллюстрация. Как понимает читатель, решение, показанное на рис. 1, годится для системы n линейных уравнений, где n может быть больше двух – равняется семи, например, что будет показано в следующей задаче.

Из повести Ф.М. Достоевского «Игрок» можно «выудить»[1] семь цитат, в которых зашифрованы курсы пяти европейских валют во времена написания повести (последняя треть 19-го века):

В «Игроке» Ф.М. Достоевского «зашифрована» система семи уравнений (семь цитат) с пятью неизвестными (пять валют), решив которую, можно узнать курс валют (талер, фридрихсдор, флорин, гульден и франк  по отношению к рублю. Вот так можно перевести на язык математики цитаты из «Игрока» Ф.М. Достоевского:

120 рублей = 100 талеров + 4 фридрихсдора + 3 флорина

700 гульденов = 700 флоринов

5 фридрихсдоров = 50 гульденов

13 000 флоринов = 8 000 рублей

4 000 флоринов = 4 000 гульденов

420 фридрихсдора = 4 000 флоринов + 20 фридрихсдоров

25 000 флоринов = 50 000 франков

Если число уравнений превышает число неизвестных, то такая система уравнений называется переопределенной.

Задачу «Игрока» также как и первую задачу, задачу Удодова можно решить без компьютера, последовательно высчитывая курсы отдельных валют (гульден равен флорину, фридрихсдор равен десяти гульденам и т.д.), а в конце решения определить их курс по отношению к рублю. Но мы, как и в случае с первой задачей, обратимся к помощи компьютера. Пусть он сам упрощает то, что считает нужным.

Рис. 3. Решение задачи о курсах валют в среде Mathcad

На рис. 3 показано решение в среде Mathcad задачи о курсах валют c использованием матрицы и вектора. Но «решающий» оператор М-1 ∙ v (векторное умножение инвертированной матрицы М коэффициентов при неизвестных системы на вектор v свободных членов) здесь работать не будет, так как матрица М в данном случае не квадратная и, следовательно, ее нельзя инвертировать. Тут на помощь приходит встроенная в Mathcad функция lsolve, которая также предназначена для решения системы линейных алгебраических уравнений, но при этом может работать и с неквадратными матрицами коэффициентов при неизвестных. Из решения, показанного на рис. 3 видно, что во второй половине XIX века талер стоил 94 копейки, фридрихсдор — 6 рублей 15 копеек и т.д. При таком раскладе генерал заплатил учителю (Алексею Ивановичу) 117 руб. 73 коп («около 120 руб.» — см. цитату 1), а «бабуленька» выиграла на рулетке 7930 руб. («до восьми тысяч дойдет» — см. цитату 4).

В задаче о курсах валют самым сложным было составить матрицу М и вектор v. Блок Given-Find при решении этой задачи будет более естественен, но не с точки зрения математики, а с точки зрения интерфейса, естественности записи условия задачи в среде Mathcad, что показано на рис. 4.

Рис. 4. Второй способ решения задачи о курсах валют в среде Mathcad

Если же число уравнений алгебраической системы меньше числа неизвестных, то такая система называется недоопределенной. Ее можно «увидеть» в описании подводной лодки «Наутилус» в романах Жюль Верна «Двадцать тысяч лье под водой» и «Таинственный остров». Вот что можно узнать из разговора капитана Немо с профессором Аронаксом о размерах подводной лодки: "Вот, господин Аронакс, чертежи судна, на котором вы находитесь. Судно представляет собой сильно удлиненный цилиндр с коническими концами. <...> Площадь его равняется одной тысяче одиннадцати и сорока пяти сотым квадратных метров, объем равен одной тысяче пятистам и двум десятым кубических метров; короче говоря, корабль, полностью погруженный в воду, вытесняет тысячу пятьсот и две десятых кубических метров, или тонн, воды.»

Если принять допущение, что центральная часть подводной лодки – это круглый прямой цилиндр, а ее нос и корма – это круглые прямые конусы одинакового размера (см. чертеж на рис. 5), то задача сводится к решению системы двух нелинейных алгебраических уравнений с тремя неизвестными (недоопределенная задача).

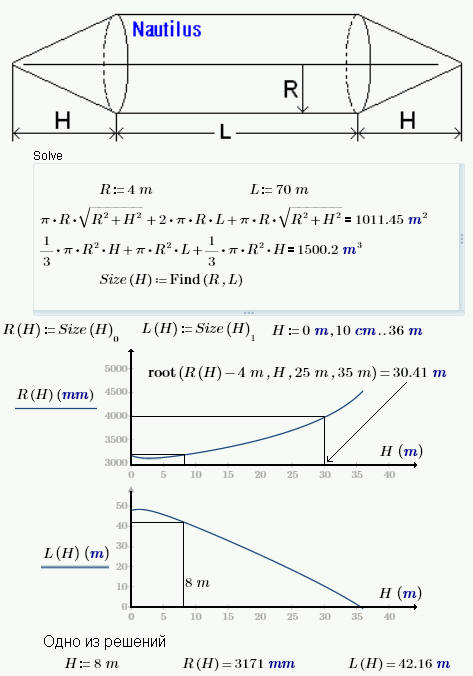
Рис. 5. Решение задачи о размерах подводной лодки

Для решения систем нелинейных уравнений в среде Mathcad есть специальный блок Solve (см. рис. 5), в котором нужно записать, во-первых, первое приближение к решению (мы тут можем предположить, что радиус цилиндрической части лодки (R) равен 4 м, а длина этого цилиндра (Н) – 70 м; от этих точек будет искаться решение задачи), во-вторых, саму систему уравнений, определяемой геометрией лодки, и, в-третьих, встроенную в Mathcad функцию Find (Найти), которая возвращает значения своих аргументов (у нас в задаче это переменные R и Н), превращающие систему уравнений в систему тождеств. Так как наша система уравнений недоопределена, то функция Find будет возвращать не конкретные значения переменных R и L, а две функции R(H) и L(H), связывающие радиус и высоту цилиндра лодки H с высотой конусов L (с длиной носа и кормы лодки). Эти две зависимости на рис. 3 отображены графически.

    Из первого графика видно, что радиус цилиндрической части лодки может меняться в пределах от 3 до 4,5 метров. Сама же (недоопределенная) задача о размерах «Наутилуса» может иметь множество решений. Одно из них (Н = 8 м, R = 3,18 м и L = 42,16 м) показано в конце решения на рис. 5 и отмечено на графиках. Дополнительно с помощью встроенной в Mathcad функции root (корень) найдено и второе решение: если б радиус цилиндра лодки R равнялся бы 4 м, то длины носа и кормы H должны быть равны 30,41 м. Значение L читатель может подсчитать сам или грубо оценить, воспользовавшись вторым графиком на рис. 5.

Послесловие 4

Цепь или трос, поддерживающий подвесной мост, описывает не гиперболический косинус, а функция, близкая к параболе. Расчет такой цепи дан здесь >>> (задана длина цепи) и здесь >>> (задано провисание цепи).

 

[1] А в эру Интернета и электронных библиотек это делать стало намного проще.


[1] Тут можно вспомнить одну историю, рассказанную Сергеем Довлатовым:

«Наш босс пришел в редакцию и говорит:

- Вы расходуете уйму фотобумаги. Она  дорогая. Можно делать фото на обычном картоне?

Генис изумился:

- Как?

- Очень просто.

- Но ведь там специальные  химические процессы! Эмульсионный слой и так далее...

Босс говорит:

- Ну хорошо, попробовать-то можно?» (источник http://lib.ru/DOWLATOW/dowlatow.txt )