1.2 Properties of state

 

Substance is usually encountered in one of the three main states: gaseous, liquid, or solid[1]. It is clear that under various conditions one and the same body or substance can exist in different states. In given permanent conditions, the considered substance will always be in one and the same state. For instance, at atmospheric pressure and a temperature of 400 °C water will exist only in the vapor state but never as a liquid or a solid.

In order to determine the concrete physical conditions under which a substance is considered and, thereby, determine unambiguously the state of this substance, convenient characteristics of the state of substance are introduced, the so-called parameters, or properties, of state.

We distinguish intensive and extensive properties of a substance. Intensive properties (pressure, temperature and some other) do not depend on the mass of substance in a system. The properties which depend on the mass of substance in a system are referred to as extensive. An example of extensive properties is volume, which changes under given conditions in proportion to the mass of substance: the volume of 10 kg of substance is 10 times greater than the volume of 1 kg of the same substance.

The specific extensive properties, i.e. properties reduced to unit mass of substance, acquire the meaning of intensive properties. So, for instance, specific volume, specific heat capacity, etc., can be considered as intensive properties. The intensive properties, determining the state of a body or of a group of bodies - the thermodynamic system - are referred to as the thermodynamic properties of the state of a body (system).

The most convenient and, therefore, the most widely used properties of state are the absolute temperature, the absolute pressure and the specific volume (or density) of a body.

One of the most important properties of state is absolute temperature. Temperature characterizes the thermal state of a body. It is common knowledge that heat can flow spontaneously only from bodies at a higher temperature to bodies at a lower temperature. Thus, the temperature of bodies determines the direction of the possible spontaneous heat exchange between these bodies[2].

Temperature is measured, for instance, with the aid of thermometers. Since the physical properties of substances depend to a greater or lesser extent on temperature, we can use as a thermometer an instrument based on accurate and easily reproducible measurements of such properties.

Each instrument used for measuring temperature must be calibrated in accordance with a commonly accepted temperature scale. The relationships between the presently used Celsius, Fahrenheit, Reaumur and Rankine temperature scales are given in Table 1.1; the most commonly used is the Centigrade (Celsius) temperature scale in which the temperature interval between two fixed points, the ice melting point (0°C) and the boiling point of water at atmospheric pressure (100 °C) is divided into one hundred equal intervals (degrees).

 

Table 1.1 Relations between Celsius, Rankine, Fahrenheit and Reaumur temperature scales

 

Scale

Celsius, oC

Rankine, oRa

Fahrenheit, oF

Reaumur, oR

Celsius, oC

-

 

 

 

 

Rankine, oRa

 

-

 

 

 

Fahrenheit, oF

 

 

-

 

 

Reaumur, oR

 

 

 

-

 

 

Of essential importance in thermodynamics is the so-called thermodynamic, or absolute, temperature scale, which shall be considered below, in Chapter 3.

The other important property of state, absolute pressure,[3] is defined as the force per unit area exerted by the substance on its surroundings. Pressure is measured in different units: the pascal (Pa)[4], the bar, the so-called technical atmosphere or simply atmosphere (1 kgf/cm2), in mm of Hg or H2O. The relations between different units of pressure are given in Table 1.2.

 

Table 1.2 Relations between different units of pressure

 

Unit

Pa

bar

kgf/cm2

mm Hg

mm H2O

1 Pa

1

10-5

1.02×10-5

7.5024×10-3

0.102

1 bar

105

1

1.02

7.5024×102

1.02×104

1 kgf/cm2

9.8067×104

0.98067

1

735

104

1 mm Hg

133

1.33×10-3

1.36×103

1

13.6

1 mm H2O

9.8067

9.8067×10-5

10-4

7.35×10-2

1

 

The specific volume of substance is the volume occupied by unit mass of a substance. The specific volume v is related to the mass of a body G and its volume V as follows:

 

                                                                                                          (1.1)

 

The specific volume of substance is usually measured in m3/kg or cm3/g.

Density

 

                                                                                                    (1.2)

 

is usually measured in kg/m3 or g/cm3.

The concept of the specific weight (gravity) of substance will sometimes be encountered in the text. By specific weight we mean the weight of substance per unit volume. In accordance with Newton's Second Law, the density and specific weight of a substance are related by the following equation:

 

                                                                                                  (1.3)

 

where g is the acceleration of gravity.

In the absence of external forces, the state of pure substance is determined unambiguously if two intensive independent properties of state are given. Any other property is a single-valued function of these properties of state. If we consider, for instance, water vapor at a temperature of 250°C and a pressure equal to 98 kPa (10 kgf/cm2), there can be only one value for the specific volume of such vapor, v = 0.2375 m3/kg. Thus, the specific volume of a gi­ven substance is determined unambiguously by the pressure p and temperature T, i.e.

 

                                                                                                  (1.4)

 

Since in determining the state of a substance all state properties "are equal in rights", the temperature of the substance will be unambiguously determined from the relation

 

                                                                                                  (1.5)

 

and the pressure from the relation

 

                                                                                                  (1.6)

 

Thus, any three properties of state (for instance, p, v or T) of a pure sub­stance are interrelated unambiguously. The equation relating the three pro­perties is referred to as the equation of state of a given substance. The relations (1.4) to (1.6) can be presented as the equation of state in the following form:

 

                                                                                                (1.7)

 

For each substance the functional relation between p, v, and T (or the values of constants present in this relation) is individual in nature; hence, the thermodynamic properties are described by an equation of state which is proper for each substance.

The relation between the properties of state can be represented by a system of coordinates p, v, T in the form of a so-called thermodynamic surface, illustrated in Fig. 1.1a.

 

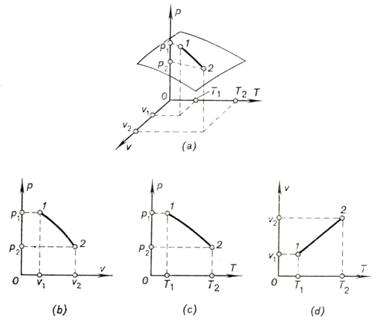
Fig.1.1.jpg

 

Fig. 1.1

 

However, the representation of the states of a system (substance) and of the processes developing in the system in space (or three-dimensional) coordinates involves a number of difficulties. That is why rectangular coordinates are usually used, with any two (of the three) properties of state taken for abscissa and ordinate. The magnitude of the third property is then determi­ned for each pair of given properties from the equation of state or by experiment.

Coordinate systems of this kind are usually referred to as the diagrams of state, or diagrams of properties. The diagrams finding the widest application in engineering thermodynamics are those with coordinates p and v (the p-v diagram Fig. 1.1b), p and T (the p-T diagram, Fig. 1.1c), and v and T (the v-T diagram, Fig. 1.1d). Below we shall get familiar with a number of other diagrams of properties, or state diagrams.

 

 

 


[1] Ionized gas, known as plasma, is sometimes believed to represent the fourth state of substance.

[2] As will be shown below, it is possible to realize the transfer of heat from a body at a lower temperature to a body at a higher temperature, but for such a process to be accomplished, an additional process should be realized, involving often an expenditure of a certain amount of work. Hence, this process of heat flow from a body at a lower tem­perature to a body at a higher temperature will not be spontaneous.

 

[3] Excess, or gauge, pressure, i.e. the difference between the absolute and barometric pressures, does not determine the state of substance and it is, therefore, not a property of state since it depends, in addition, on the state of the surrounding medium (its pressure).

[4] It will be recalled that the pascal is the pressure exerted by a force of 1 N uniformly distributed over an area of 1 m2. Since 1 N = 1 kg-m/s2, it follows that 1 Pa = 1 kg/(m-s2). Along with the pascal greater units are used, the kilopascal (kPa) and the megapascal (MPa): 1 Pa = 10-3 kPa = 10-6 MPa.