1.3 Concept of a
thermodynamic process
A thermodynamic system is denned as a totality of material bodies
interacting both with one another and with the external medium. All other
material bodies arranged outside the boundaries of the system considered are
said to constitute the surroundings.
If only one of the
properties of state changes, the state of the system changes as well, i.e. a thermodynamic process representing the totality of the changing states of
the system takes place.
All processes occurring in
a thermodynamic system can be divided into equilibrium and non-equilibrium
processes. An equilibrium (quasi-static) process is denned as a thermodynamic process in which the system undergoes a
continuous succession of equilibrium states (the equilibrium state of a system
is considered in detail in Chapter 5; it is characterized, in particular, by
the fact that all parts of the system are at the same temperature and
pressure). A non-equilibrium process is defined as a thermodynamic process in which the
system is not in a state of equilibrium (i.e. in the process various parts of
the system are at different temperatures, pressures, and have different
densities, concentrations, etc.).
The process occurring in a
system will be the closer to an equilibrium one the shorter the time (compared
with the characteristic time of the process) it takes the system to return to a
state of equilibrium after a disturbance related to the development of the
process.
Let us expound these
concepts by considering the following example. Consider a vessel separated into
two parts by a partition; one of the parts is filled with a gas under pressure,
and in the other part a vacuum is maintained. If the partition is removed, the
compressed gas will expand in the vessel, occupying the entire volume of the
vessel and a uniform pressure will set in the vessel. This process is a typical
non-equilibrium process; throughout the entire process the gas will be at
different pressures in different parts of the vessel: first the layers of the
gas adjacent to the partition will undergo expansion, then the following
layers, etc.
If a gas is compressed in a cylinder with the
aid of a piston acted upon by external pressure, the pressure acting upon the
piston must exceed somewhat the pressure of the gas filling the cylinder. This
is due to the fact that with the piston moving at a finite velocity, first the
layers of gas closer to the piston will be compressed; hence, these layers shall
be under a pressure exceeding the mean pressure of the gas in the cylinder.
This change in pressure (sometimes referred to as the disturbance) caused by
the moving piston is not propagated instantaneously but at a finite velocity[1]. Before this disturbance propagates over the
entire volume of the cylinder, the piston has time to move through a certain
distance and the pressure of the gas near the piston rises again, etc. It is
this higher pressure, the pressure of the gas which is in direct contact with
the piston, that will oppose piston travel. Thus, while the gas is being
compressed from an initial to a final pressure, the pressure of the gas inside
the cylinder will differ in the various parts of the volume filled by the gas,
and hence non-equilibrium compression of the gas will take place: there is no
equilibrium both inside the space occupied by the gas being compressed and in the
entire system (compressed gas + piston + surroundings acting upon the piston).
It should also be noted that the additional difference between the external
pressure acting upon the piston and the pressure of the gas in the cylinder is
due to the fact that since, as the piston travels, the layers of the gas
undergoing compression in the cylinder also move at definite velocities, an
additional force is required, imparting these velocities to the moving layers
of gas (the kinetic energy of these layers is expended to overcome the forces
of viscous friction in the gas proper and skin friction occurring between the
gas and cylinder walls).
It follows from the
foregoing that, as a rule, the higher the rate of the process, the greater the
irregularity occurring in the system while the process is being accomplished.
In particular, in the process of gas compression in a cylinder considered
above, the difference in pressure at various points in the cylinder and
respectively the difference in the pressures on both sides of the piston will
be the greater, the higher the piston velocity. If the piston velocity is quite
low, the pressure of the gas at various points in the cylinder will differ but
slightly, with the required external excess pressure acting upon the piston
being also of a rather small magnitude. In other words, the lower the rate at
which the process proceeds, the closer the process to an equilibrium one.
Any real process is a
non-equilibrium one to a greater or lesser degree. In principle, however, this
departure from equilibrium can be made as slight as desirable by reducing the
rate of the process. Thus, an equilibrium process is the extreme, or limiting,
case of a non-equilibrium process with the rate of this process tending to
zero. That is why equilibrium processes are sometimes referred to as
quasi-static processes.
From here on by the word
"process" we shall mean an equilibrium process. When considering
non-equilibrium processes, we shall state this explicitly.
If a system consists of a
pure substance, its state, as it was mentioned above, is represented by some
surface in the system of p, v, T coordinates. The process of
transition of this system from state 1 (where the properties of the substance are p1, v1, T1) into state 2 (with properties p2, v2, T2) will be graphically represented by line 1-2 on the surface of state of the given substance (Fig. 1.1a). Line 1-2 representing the change in properties in the process, is called the path of the process. Each point on the path of the process characterizes
an equilibrium state of the system. It is possible to represent graphically
only processes in which the system passes through a continuous succession of
equilibrium states, i.e. only equilibrium processes can be represented
graphically.
It is clear that the paths
of a process can also be represented or plotted on plane diagrams of
properties. The path of the process 1-2 is projected from the surface of state, shown in Fig. 1.1a on the p-v, p-T and v-T diagrams in Fig. 1.1b, c, d.
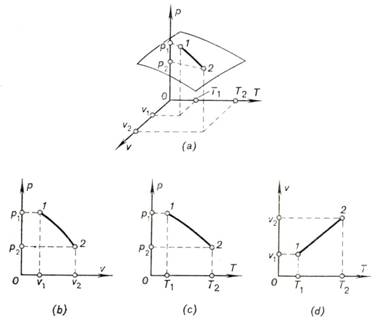
Fig.
1.1
An equilibrium process in
the course of which the system's temperature remains constant is known as an isothermal (constant-temperature) process. An example of an isothermal
process is the boiling of pure water in an open vessel: until all the water boils
out of the vessel, its temperature remains practically constant (provided
atmospheric pressure does not change in the process of boiling).
An equilibrium process
proceeding at a constant pressure is said to be an isobaric (constant-pressure) process. An isobaric process can be
exemplified by the process of heating water in an open vessel; the pressure of
the heated water then remains constant and equal to atmospheric pressure,
whereas water temperature rises and the specific weight (gravity) of the water
changes.
An equilibrium process
proceeding at constant volume is called an isochoric (constant-volume) process. An example of an isochoric
process is the heating of water in a closed vessel. In the course of heating
the volume of the vessel remains practically constant (should we neglect some
expansion of the vessel upon heating), whereas the temperature of the water in
the vessel increases and water pressure rises.
An equilibrium process in
the course of which heat is not added into a thermodynamic system from the
surroundings (and is not rejected to the surroundings) is called adiabatic; in a process of this kind there is no heat exchange between the system
and the surroundings. The lower the conductivity of the insulation of the
system, the closer the process is to an adiabatic one.
The curve (path) of an
isothermal process is called the isotherm, the curve of an isobaric process the
isobar, the curve of an isochoric process the isochor, and the curve of the
adiabatic process is called the adiabatic curve. Below in the book we shall get
familiar with a number of other equilibrium thermodynamic processes.