1.5 Concept of mixtures. Mixtures of ideal gases

Pure substances and mixtures

In thermodynamics the concepts of a pure substance and a mixture (solution) is used. By a pure substance we mean a substance all molecules of which are similar, or a substance which does not change chemically. A mixture, consisting of several pure substances, is referred to as a solution. Examples of pure substances are water, ethyl alcohol, nitrogen, ammonia, sodium chloride, and iron. Examples of mixtures are air, consisting of nitrogen, oxygen and a number of other gases, aqueous ammonia solutions, aqueous solutions of ethyl alcohol, various metal alloys. The pure substances making up a mixture are called components or constituents.

Determining the composition of a mixture

One of the most important characteristics of a mixture is its composition. The composition of a mixture is usually determined by finding the mass and molar fractions of the individual mixture components.

Let us consider a mixture consisting of G₁ kg of the first component, G₂ kg of the second component, G₃ kg of the third component, etc. The total mass of a mixture consisting of n components will be

(1.34)

The mass fraction of each component is defined as the ratio of the mass of the given component to the mass of the entire mixture

(1.35)

It follows from Eqs. (1.34) and (1.35) that

(1.36)

Consequently, the mass fraction can be determined by the fraction of the given component contained in 1 kg of the mixture.

For a mixture consisting of two components (referred to as a binary mixture)

Therefore, the composition of the mixture is known if the mass fraction of one of the components is given. In a binary mixture, the mass fraction of the second component is usually denoted by c, and it is then evident that the mass fraction of the second component is (1 - c). Thus, for a binary mixture

(1.37)

It is sometimes more convenient to determine the composition of a mixture by means of molar fractions. By a molar fraction of a mixture component is meant the ratio of the number of moles of the component considered to the total number of moles of the mixture.

Let a mixture contain M₁ moles of the first component, M₂ moles of the second component, M₃ moles of the third component, etc. The number of moles of the mixture is equal to

(1.38)

and the molar fraction of the i^th component

(1.39)

In accordance with Eqs. (1.38) and (1.39),

(1.40)

Thus, the molar fraction of a given component in a mixture can be defined as the number of moles (the fraction of a mole of this component) in one mole of the mixture:

Just as for mass fractions, the letter N is used below to denote the molar fraction of the second component in a binary mixture, and the molar fraction of the first component is denoted by (1 - N). Then,

(1.41)

The relation existing between the mass and molar fractions permits, if necessary, to express one fraction in terms of the other. In order to find this relation, let us consider a mixture with an arbitrary number of components. If the molecular masses of the first, second, third, etc., components are respectively denoted by µ₁, µ₂, µ₃, . . ., µ_n, then the mass fraction of the i^th component, c_i, can be expressed in terms of the molar fractions in the following way:

(1.42)

If the mass fractions of the components of a given mixture are known, the expression which can be used to determine the molar fraction N_i of any i^th component of the mixture takes the form:

(1.43)

For a binary mixture, from Eqs. (1.42) and (1.43) it follows that for the first component

and

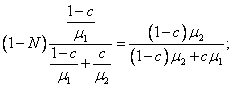(1.44)

for the second component

and

(1.45)

Mixtures of ideal gases. Dalton's law

Mixtures of various gases, the so-called gas mixtures, are considered as special cases of mixtures (solutions). It is of great interest to examine a gas mixture each component of which considered as an ideal gas. The idea of considering mixture components as ideal gases happens to be a good approximation for quite a number of gas mixtures at low pressures. Of such gas mixtures, air is of the greatest practical importance.

The basic law determining the behavior of a gas mixture is Dalton's law: Each individual gas behaves in a gas mixture as though it alone occupies the volume of the mixture at the mixture temperature.

In other words, each individual component of a gas mixture is under the pressure which it would exert if it alone occupied the volume of the mixture. This pressure is called the partial pressure of the given gas, and the partial pressure of each mixture component is respectively denoted by p₁, p₂, p₃, . . . . . ., p_n. At first glance it may seem strange that it is indifferent for the given gas component whether there are any other gases in the volume or it alone occupies the space. However, there is nothing strange in the phenomenon, since we are dealing with ideal gases and, as mentioned above, the molecules of an ideal gas are, by definition, material points devoid of volume and not interacting with one another in any way, except by collision. The higher the pressure in a mixture, i.e. the more the states of the gases deviate from the ideal state, the more the behavior of the gas mixture is observed to deviate from that prescribed by Dalton's law. Dalton's law can also be stated as follows:

The sum of the partial pressures of the ideal gases which are components of a gas mixture is equal to the total pressure of the mixture of gases:

(1.46)

Dalton's law finds wide application in describing various mixtures of gases, and it will be repeatedly used in the book.

Composition of an ideal gas mixture. Volume fractions

If a component of an ideal gas mixture is not at its partial pressure at the temperature of the mixture but the total pressure of the mixture is exerted on it, its volume is V_i, which is referred to as the partial volume of the i^th gas component. The ratio between the partial volume and the volume of the mixture is called the volume fraction of the given component:

(1.47)

The partial volume is determined from Boyle's law

where p_mix and V_mix are the pressure and volume of the mixture;

whence

Since

we get

or (1.48)

Thus, the total volume of a mixture of gases is equal to the sum of the partial volumes of its components.

If a gas comprises M₁, M₂, . . ., M_i moles of different gases, the volume fraction of the i^th component is equal to:

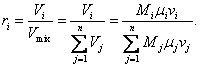(1.49)

Since for all gaseous components of the gas mixture, reduced to the same pressure p_mix and the same temperature T_mix, the volume of the moles is the same, we have

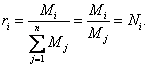(1.50)

Thus, the volume fraction of the component of a mixture of ideal gases is equal to the molar fraction of this component.

It follows from this that Eqs. (1.42) and (1.43) can be presented in the following form:

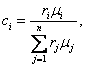(1.51)

(1.52)

Apparent or average molecular (molar) mass of a mixture

In calculating mixtures of ideal gases, it is convenient to make use of the so-called apparent or average molecular (molar) mass of the mixture, which is the ratio of the mass of the mixture to the total number of moles of all mixture components:

(1.53)

Taking into account Eqs. (1.30), (1.35) and (1.38), we find that

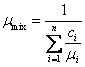(1.54)

and

(1.55)

Gas constant of a mixture

For the i^th component of a mixture of ideal gases with a volume V_mix Clapeyron's equation will obviously take the form

Writing this equation for all components of the mixture and summing the left-hand and right-hand sides, we get:

(1.56)

In accordance with Dalton's law, ,whence

(1.57)

On the other hand, for a mixture of ideal gases Clapeyron's equation can obviously take the following form:

(1.58)

where R_mix is the gas constant of the mixture.

It follows from Eqs. (1.57) and (1.58) that

(1.59)

Since

from Eq. (1.59) we get

(1.60)

whence, with account taken of Eq. (1.57), we should get:

(1.61)

Substituting µ_mlx from Eq. (1.55), we obtain:

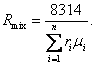(1.62)

Determining partial pressures

Since p_iV_mix = p_mixV_i and V_i/V_mix = r_i,

and

(1.63)