10.2 Gas turbine cycles

One of the main drawbacks inherent in reciprocating internal combustion engines is the need for a crank gear and flywheel and the inevitable irregularity of crankshaft rotation. These shortcomings make it impossible to concentrate a high capacity in one unit, restricting the application of reciprocating engines.

Another type of internal combustion engine, the gas turbine, is free from this drawback. Possessing a high thermal efficiency and at the same time possessing all the advantages of a rotary engine, i.e. the possibility of concentrating large capacities in small units, the gas turbine has great potential. Currently, the application of gas turbines in highly efficient power plants is limited chiefly because the insufficient heat resistance of up-to-date structural materials permits the dependable operation of gas turbines only at temperatures considerably inferior to those characteristic of reciprocating internal combustion engines, resulting in a lower thermal efficiency of the plant. Further progress in making new strong and heat-resistant materials will make it possible to operate gas turbines at higher temperatures.

Presently, gas turbines are used in aviation, marine power plants, railroad transport and are being gradually introduced into power-generating. Gas turbines are divided into two main types:

(i) constant-pressure (combustion) gas turbines (p = const),

(ii) constant-volume (combustion) gas turbines (v = const).

Thus, gas turbines are classified by the method of fuel combustion in the same way as reciprocating internal combustion engines.

The schematic diagram of a constant-pressure gas-turbine plant is given in Fig. 10.12. Mounted on a common shaft are gas turbine 1, compressor 2, fuel pump 3 and power consumer 4 (represented by the symbol of a three-phase a.c. generator). The compressor draws atmospheric air, compresses it to the pressure required and directs the compressed air into combustion chamber 5 into which the fuel pump delivers fuel from tank 9. Liquid and gaseous fuels are suitable. In gas-fired gas turbines the pump is replaced with a gas compressor.

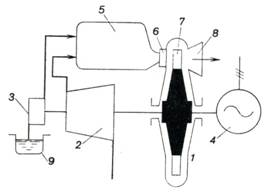
Fig. 10.12

Fuel combustion proceeds in the combustion chamber at p = const. The products of combustion, expanding in the nozzles 6 of the gas turbine, hit the turbine blades 7, and produce work on the blades; the waste gas is then exhausted into the atmosphere through exhaust duct 8. The pressure of the exhaust gas somewhat exceeds atmospheric pressure.

The ideal cycle of the gas-turbine plant under consideration is plotted on the p-u diagram in Fig. 10.13.

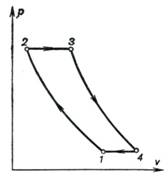
Fig. 10.13

The construction principle of this ideal cycle does not differ from that of the cycles of reciprocating engines: the cycle is assumed to be closed, i.e. the amount of the working medium is constant throughout the cycle. The discharge of the waste gas into the atmosphere is replaced by an isobaric process with heat rejection to a low-temperature source; it is assumed that heat q₁ is added to the working medium from an external source, through the walls of the turbine casing. It is also assumed that the working medium is a gas of constant composition such as pure air. On the indicator diagram shown in Fig. 10.13 process 1-2 represents the compression of air in the compressor (as was shown in Sec. 7.9, the process of compression can be adiabatic, isothermal, or polytropic). Heat is added to the working medium along the isobar 2-3 (this process corresponds to the combustion of fuel in the combustion chamber). The working medium (air and combustion products in the real cycle) then expands adiabatically in the turbine nozzles and transfers work to the turbine wheel (process 3-4). The isobaric process 4-1 corresponds to the exhaust of the waste gas from the turbine[1].

Let us determine the thermal efficiency of the cycle of a constant-pressure combustion gas turbine, sometimes referred to as the Brayton cycle. Just as before, the working medium is assumed to be an ideal gas with a constant heat capacity.

The thermal efficiency of this gas turbine will differ, depending on whether the process of compression accomplished is isothermal, adiabatic, or polytropic.

Let us consider first the cycle of a constant-pressure combustion gas-turbine plant with isothermal compression[2] of air in the compressor. The T-s diagram of this cycle is depicted in Pig. 10.14.

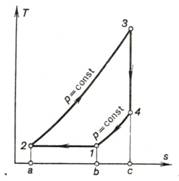
Fig. 10.14

In this case heat will also be rejected from the working medium to the low-temperature source in the isobaric process 4-1 (area b-1-4-c-b in Fig. 10.14) and in the process of isothermal compression 1-2 (area a-2-1-b-a), with the quantity of heat rejected during the isobaric process 4-1 being

(10.34)

and the quantity of heat rejected during the isothermal process 1-2 being [in accordance with Eq. (7.22a)]

(10.35)

Thus, the total amount of heat rejected is

(10.36)

The quantity of heat added to the working medium in the isobaric process 2-3 is

(10.37)

Substituting these values of q₁ and q₂ into the general relation for the thermal efficiency,

we obtain:

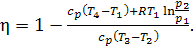(10.38)

Dividing the numerator and the denominator of the right-hand side of Eq. (10.38) by c_pT₁ and having in mind that for an ideal gas

we obtain:

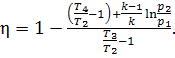(10.39)

The notation of the degree of preliminary expansion, p = v₃/v₂, introduced in the preceding section, will also be used below.

Let us denote the ratio of the pressure at the end of expansion to the pressure at the beginning of the process by

(10.40)

This quantity is called the pressure ratio of the process of compression. It is clear that in the isobaric process 2-3

(10.41)

and that in the adiabatic process 3-4

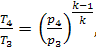(10.42)

or, which is the same (since p₃ = p₂ and p₄ = p₁),

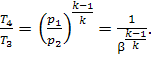(10.43)

Substituting Eqs. (10.41) and (10.43) into Eq. (10.39) and taking into account that

we obtain the expression for the thermal efficiency of a gas turbine operated with constant-pressure combustion (isothermal compression of air):

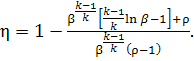(10.44)

The dependence of the thermal efficiency η on ρ for various values of β (at k = 1.35), described by Eq. (10.44), is presented graphically in Fig. 10.15.

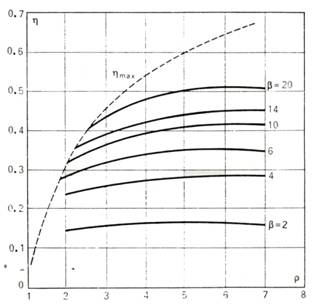
Fig. 10.15

Equation (10.44) can be used to find the maximum value of the thermal efficiency for different degrees of preliminary expansion ρ. For this purpose take the first derivative of the thermal efficiency with respect to the pressure ratio β at ρ = const. After doing the required transformations we obtain

(10.45)

Equating this expression with zero, we obtain the following condition for the maximum thermal efficiency:

(10.46)

It will be noted that at the cycle is represented graphically by a triangular diagram.

Replacing in Eq. (10.44) β with its value from Eq. (10.46), we obtain the maximum thermal efficiency at a given ρ:

(10.47)

On the graph shown in Fig. 10.15 the line of maximum efficiencies is represented by the dotted line[3].

Consider now the cycle of a constant-pressure combustion gas turbine (p = const) for the adiabatic compression of air in the compressor of the gas-turbine plant. The T-s diagram of this cycle is shown in Fig. 10.16.

Fig. 10.16

In this case

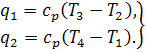(10.48)

It follows from (10.48) that the thermal efficiency of this cycle is determined from the expression

(10.49)

or

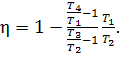(10.50)

The temperature ratios present in Eq. (10.50) are easily expressed in terms of ρ and β. Indeed, for the adiabatic process 1-2

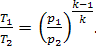(10.51)

On the other hand, from the fact that p₃ = p₂ and p₄ = p₁ it follows that

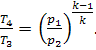
Thus, for this cycle,

(10.52)

and

or

(10.53)

The thermal efficiency of this cycle is plotted in Fig. 10.17 as a function of β at k = 1.35.

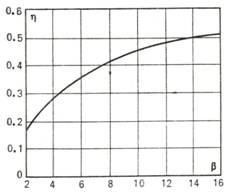
Fig. 10.17

A comparison of the effectiveness of cycles realized in constant-pressure combustion gas turbines for isothermal and adiabatic compression, conducted with equal amounts of added heat q₁, maximum pressures p₃ and maximum cycle temperatures T₃ (inasmuch as in the two cases the initial cycle pressure p₁ is equal to atmospheric, the condition of equality of pressures p₃ corresponds to the condition of equality of the pressure ratios β), shows the thermal efficiency of the cycle with adiabatic compression to exceed that of the cycle with isothermal compression:

(10.54)

This conclusion can be easily deduced by plotting the cycles being analyzed on a common

T-s diagram shown in Fig. 10.18. In accordance with the conditions of comparison previously assumed, the pressure in the process of heat addition (2-3) and the pressure during the exhaust process (4-1'-1) are the same in both cycles, as well as the values of q₁ and T₃. It is clear from the T-s diagram that the work output of the cycle with adiabatic compression (area 1-2-3-4-1) is greater than the work output of the cycle with isothermal compression (area 2-3-4-1'-2). With the same value of q₁ it leads to the inequality (10.54).

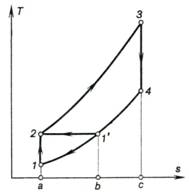
Fig. 10.18

It is clear that when a constant-pressure combustion gas turbine is operated with polytropic air compression and an exponent 1 < n < k, its thermal efficiency will fall between and .

The thermal efficiency of a constant-pressure combustion gas turbine (p = const) can be increased by practising heat regeneration.

The concept of heat regeneration was introduced in Sec. 3.6 when considering reversible cycles. It was shown that regeneration raises the thermal efficiency of a cycle since the area ratio increases. The schematic diagram of a gas-turbine plant incorporating a constant-pressure combustion gas turbine with heat regeneration is shown in Fig. 10.19.

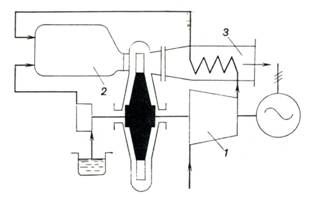
Fig. 10.19

A gas-turbine plant with heat regeneration differs from one without heat regeneration in that the compressor 1 does not discharge compressed air directly into the combustion chamber 2 but first passes it through the heat exchanger 3 where it is heated by the exhaust gases. Correspondingly, before being rejected into the atmosphere, the exhaust gases pass through the heat exchanger where they are cooled heating the compressed air. Thus, a certain fraction of the heat, previously lost with the exhaust gases, is now utilized in the turbine operated on the regeneration cycle.

The regenerative cycle of a constant-pressure combustion gas-turbine plant is shown in Fig. 10.20.

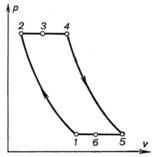
Fig. 10.20

This cycle involves either isothermal or adiabatic air compression in the compressor 1-2, process 2-3 ensuring isobaric heating of the air in the regenerator (heat exchanger), isobaric process 3-4 corresponding to heat addition in the combustion chamber upon fuel combustion, process 4-5 of adiabatic expansion of gases in the turbine, isobaric cooling of the exhaust gas in the heat exchanger in process 5-6, and finally, the hypothetical isobaric process 6-1, closing the cycle.

The completeness of heat generation is usually determined by the degree of regeneration, or the regeneration fraction

i.e. by the ratio of the heat which was actually utilized in the process of regeneration (process 2-3) to the heat available, corresponding to the possible temperature difference, T₅ — T₂.

The quantity of heat transferred to the compressed air in the regenerator should naturally be equal to the amount of heat lost by the exhaust gases in the regenerator, i.e.

(10.55)

Thus, taking into account the previously assumed condition that the heat capacity of air does not change with temperature, we get:

(10.56)

Let us denote by γ = T₃/T₂ the ratio of the air temperature at the heat-exchanger outlet, T₃, to the air temperature at the heat-exchanger inlet, T₂. In the limiting case of complete regeneration it is clear that the temperature T₃ = T₅ and, consequently, the degree of regeneration σ = 1. For this case there is a limiting value γ_max:

(10.57)

Let us now consider the regenerative cycle of a constant-pressure gas turbine with isothermal air compression. Figure 10.21 shows this cycle on a T-s diagram. In the presence of regeneration, the heat rejected along section 5-6 of isobar p₂ = const is added to the working medium along section 2-3 of isobar p_x = const (consequently, on the T-s diagram shown in Fig. 10.21 area c-6-5-d-c is equal to area a-2-3-b-a); in Fig. 10.21 this process is indicated by an arrow.

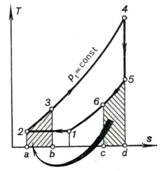
Fig. 10.21

The heat added in this cycle is

(10.58)

the heat rejected is

(10.59)

The amount of heat rejected with the exhaust gases can be determined taking into account Eq. (10.55):

(10.60)

Then,

(10.61)

The thermal efficiency can now be determined as

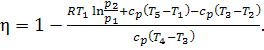(10.62)

Dividing the numerator and denominator of Eq. (10.62) by c_pT₁ and allowing for T₁ = T₂, we obtain:

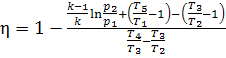. (10.63)

Denoting the ratios and we now determine the values of the temperature ratios in Eq. (10.63), taking into account that

(10.64)

Then,

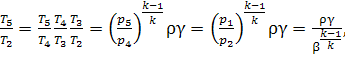(10.65)

(10.66)

Replacing in Eq. (10.63) for the thermal efficiency the pressure and temperature ratios with their notations β, ρ and γ, we get:

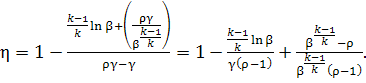(10.67)

It follows that the greater γ is (γ characterizes the degree of regeneration), the higher is the thermal efficiency of a constant-pressure combustion gas-turbine plant.

With a maximum degree of regeneration, σ = 1 and, consequently, γ_max = T₅/T₂ = T₅/T₁. All the heat available in the exhaust gases is then utilized to heat the compressed air. Such regeneration is referred to as complete. It is clear that this case is only of theoretical importance, since at a zero temperature difference between the exhaust gases and air, which would have taken place in the event of complete regeneration, no heat transfer is possible in the regenerator, the heat exchanger. Figure 10.22 shows the cycle with complete regeneration on a T-s diagram. It is clear that area a-2-3-b-a equals area c-1-5-d-c. In this case at T₃ = T₅ the degree of preliminary expansion will be:

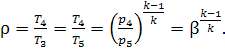(10.68)

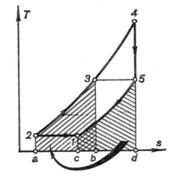
Fig. 10.22

Substituting (10.68) into Eq. (10.67), we obtain:

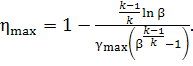(10.69)

It follows that the thermal efficiency of a constant-pressure combustion gas-turbine plant operating with complete regeneration does not explicitly depend on ρ. Since the limited degree of regeneration of the given cycle is expressed in terms of γ_max = T₅/T₁ the thermal efficiency of this cycle can be directly determined by the temperature at the end of expansion, T₅, i.e.

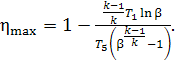(10.70)

The higher the temperature T₅, the higher the thermal efficiency of the cycle. Equation (10.70) shows the necessity of raising the temperature T₅ at the end of expansion which unfortunately is hampered due to the comparatively low mechanical strength of the materials of gas-turbine blades at high temperatures.

The thermal efficiency of the cycle of the given gas-turbine plant operating with complete regeneration is plotted as a function of the pressure ratio β at different values of T₅ in Fig. 10.23.

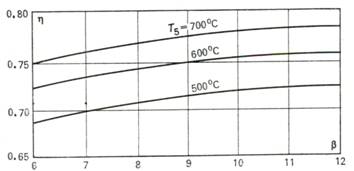
Fig. 10.23

It can be easily shown that regeneration increases the thermal efficiency of a cycle, as is clear, for instance, from the T-s diagram shown in Fig. 10.22. In fact, the work output per cycle of a gas-turbine plant, l_c, will be the same both with and without regeneration (this work is represented by area 1-2-3-4-5-6-1), whereas the heat q₁ added in the cycle will be represented by area a-2-3-4-5-d-a for the cycle without regeneration, and by area b-3-4-5-d-b, for the cycle with regeneration.

Taking into account the fact that area b-3-4-5-d-b is smaller than area a-2-3-4-5-d-a, it follows from the equation for thermal efficiency presented in the form

that the thermal efficiency of the regenerative cycle is higher than that of the cycle without heat regeneration.

Now let us determine the thermal efficiency of a constant-pressure combustion gas-turbine plant operated on a regenerative cycle with adiabatic air compression. Fig. 10.24 shows the cycle on a T-s diagram. The heat transferred from the exhaust gases in the regenerator is represented by area c-6-5-d-c and the heat added to the compressed air passing through the heat exchanger, by area a-2-3-b-a.

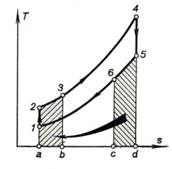
Fig. 10.24

The added heat is

(10.71)

the rejected heat is

(10.72)

but since

we have:

(10.73)

The thermal efficiency of the cycle will then have the following form:

(10.74)

Dividing the numerator and denominator of Eq. (10.74) by c_pT₁, we obtain:

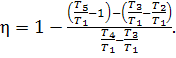(10.75)

Let us express the temperature ratios in Eq. (10.75) in terms of ρ, β and γ. The equations of the adiabats give the following for the processes 1-2 and 4-5:

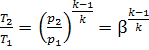
and

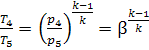
i.e.

or

Thus,

Therefore

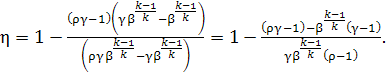(10.76)

The maximum possible degree of regeneration, or regeneration fraction occurs at T₃ = T₅, i.e. at γ_max = T₅/T₂. A cycle with a maximum degree of regeneration is shown on a T-s diagram in Fig. 10.25. Just as on the T-s diagram in Fig. 10.24, the heat rejected from the exhaust gas in the regenerator is represented by area c-6-5-d-c, and the heat added to the compressed air passing through the regenerator by area a-2-3-b-a.

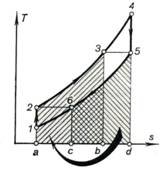
Fig. 10.25

In this case we have

and

Then

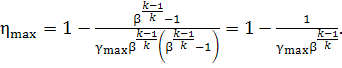(10.77)

Formula (10.77) can be transformed to show the dependence of the maximum thermal efficiency on gas temperature at the end of expansion, or T₅.

As is known, with a maximum degree of regeneration

thus

(10.78)

Thus, the thermal efficiency of a constant-pressure gas-turbine plant operating with maximum regeneration[4] and adiabatic compression depends only on the temperature of the gas at the end of adiabatic expansion, T₅, an important characteristic determining the design of a turbine (the initial gas temperature T₁ is usually assumed constant). The maximum thermal efficiency is plotted in Fig. 10.26 as a function of final temperature T₅, with T₁ = 300 ^oC.

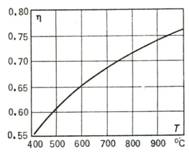
Fig. 10.26

Let us now compare two gas-turbine cycles, with isothermal compression and complete regeneration and with adiabatic compression and maximum regeneration, both cycles being realized at different initial pressures and temperatures and at the same maximum pressures and temperatures (with the temperatures at the end of expansion being the same for the two cycles, as shown in Fig. 10.27).

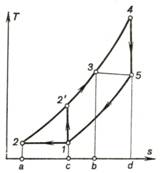
Fig. 10.27

The thermal efficiency of the cycle with isothermal compression and complete heat regeneration

and the thermal efficiency of the cycle with adiabatic compression and maximum heat regeneration

Since in this case equal amounts of heat q₁ (area b-3-4-d-b) are added to the working medium from an outside source, and the work outputs of the two cycles are different, with the cycle, involving isothermal compression producing more work (area 1-2-4-5-1 is greater than area 1-2'-4-5-1), the thermal efficiency of the cycle with isothermal compression and complete regeneration is always greater than the thermal efficiency of the cycle with adiabatic compression and maximum regeneration.

Thus, with a maximum possible heat regeneration, isothermal compression is more expedient than adiabatic.

Along with the constant-pressure combustion gas turbine, constant-volume combustion gas turbines can also be constructed. The schematic diagram of such a gas-turbine plant is given in Fig. 10.28, and Fig. 10.29 shows the cycle of such a plant on a p-v diagram. Compressor 2, sharing a common shaft with turbine 1 proper, compresses atmospheric air to the pressure required (process 1-2). Air can be compressed both isothermally and adiabatically. A fuel pump or compressor 3 delivers liquid or gaseous fuel and the compressed air into combustion chamber 4. Sometimes the fuel and air are not delivered into the combustion chamber in separate streams, but as a combustible mixture (fuel-air mixture preliminarily prepared in a carburetor). With the valves closed the fuel is usually ignited in the combustion chamber from spark plug 8. Fuel combustion (process 2-3) proceeds at a constant volume. After fuel combustion is terminated the exhaust valve opens and the products of combustion pass into nozzle 5 of the turbine where they expand adiabatically (process 3-4) to atmospheric pressure. The gases leaving the nozzles flow onto blades 6 of the turbine, perform work and are discharged into the atmosphere through the turbine exhaust duct 7. The useful work produced by the plant is transferred to energy (power) consumer 9. The cycle is closed by a hypothetical isobaric process 4-1.

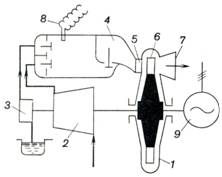
Fig. 10.28

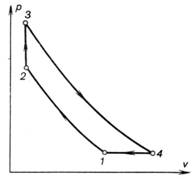
Fig. 10.29

Notwithstanding their somewhat higher thermal efficiency, constant-volume combustion gas-turbine plants are less widespread than constant-pressure combustion gas turbines. This is usually explained by the lower absolute brake thermal efficiency of the constant-volume combustion gas turbine compared with the absolute efficiency of the constant-pressure combustion gas-turbine plant, in spite of its higher thermal efficiency. The latter is mainly due to the uneconomical performance of the turbine traced to the fact that the properties of the gas flowing into the turbine vary with time. In addition, the design of constant-volume combustion gas turbines is far more complicated than that of gas turbines in which combustion proceeds at a constant pressure, p = const.

Both the reciprocating internal-combustion engines and the gas-turbine plants, whose cycles were investigated above, operate on an open cycle and are referred to as open-cycle machines. In the cycles of the internal combustion turbines considered, the compressor draws air from the atmosphere, and the exhaust gases are discharged into the atmosphere from the turbine outlet (or from the regenerator outlet in gas-turbine plants operating on the regenerative cycle). In this way, in these plants each new cycle is realized with a fresh portion of the working medium. As was already mentioned, these cycles were hypothetically plotted and investigated on p-v and T-s diagrams as closed cycles.

It is possible, however, to realize an actually closed cycle, possessing in a number of cases certain advantages over the open cycle. The schematic diagram of a constant-pressure gas turbine plant operated on a closed cycle is illustrated in Fig. 10.30. Compressor 1 compresses the working medium to the pressure required and forces the compressed working medium to flow into regenerator (heat-exchanger) 2 where it is heated at p = const by the hot exhaust gases leaving the turbine. The heated working medium then flows from the regenerator into heat exchanger 3 where heat is added from an external source. The heat exchanger is basically similar to a steam boiler in which gas is heated, instead of water and steam. Heat is added in the heater by the fuel delivered by fuel pump 4 (if liquid fuel is fired) and burned in the combustion chamber. The air required for fuel combustion is delivered by fan 5, and is preheated in heater 3 by the heat contained in the exhaust gases. The working medium, heated in heater 3 at p = const, passes into turbine 6 where it expands and produces work. The exhaust gases are directed from the turbine into the regenerator in which a fraction of their heat is transferred to the compressed gas coming from the compressor.

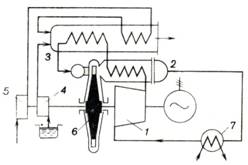
Fig. 10.30

From the regenerator the waste gases are directed into cooler 7 where they are cooled to the lowest cycle temperature at p = const. Water is usually used as a coolant. From the cooler the working medium is sent again into the compressor. Thus, the same portion of the working medium is continuously engaged in producing work.

From the point of view of thermodynamics the operating cycle of this gas-turbine plant is similar to the regenerative constant-pressure combustion cycle previously analyzed. Therefore all the formulas for the thermal efficiency of a regenerative constant-pressure combustion cycle derived above are applicable to the closed cycle. We shall examine the advantages and drawbacks of the closed cycle, compared with an open cycle. Since a constant amount of the working medium is involved in the operation of the closed-cycle gas turbine, not only air and combustion products but any gas can be used as a working medium. Let us consider the advantage of replacing air with another working medium.

The formulas for the thermal efficiency of a cycle derived above with heat addition at

p = const and heat regeneration present the thermal efficiency of the cycle as a function of not only β, ρ and γ but, under otherwise identical conditions, of the type of the working medium. Indeed, apart from β, ρ and γ, all expressions for the thermal efficiency contain the adiabatic exponent k which depends chiefly on the atomicity of the gas involved[5].

This indicates the effect of the properties of the working medium used in the closed cycle on its thermal efficiency.

An analysis of the Eqs. (10.67) and (10.76) for the thermal efficiency of this cycle shows that with the same β, ρ and γ an increase in the adiabatic exponent leads to a higher cycle efficiency. On the other hand, it is clear that when a gas with a greater adiabatic exponent is used at the same value of the thermal efficiency and the same ρ and γ, the cycle can be realized with a smaller pressure ratio.

For this reason, since it permits the use of a working medium with a maximum adiabatic exponent, the closed cycle has definite advantages. Such working fluids can be primarily monatomic gases, helium and argon (it will be recalled that for an ideal monatomic gas k = 1.67, whereas for air we assume an exponent k = 1.35).

On the other hand, the closed cycle permits operation with cycle pressures most advantageous technically and economically. If the lowest pressure in an open-cycle gas turbine is atmospheric pressure, then in the closed cycle realized with the same pressure ratio the initial cycle pressure can be considerably higher than atmospheric pressure. This permits operation at higher pressures, which leads to a considerable reduction in the volumes of the gases flowing through the components of a gas turbine, smaller heat exchange surfaces are required and the task of creating high-power gas-turbine plants is greatly facilitated.

To raise the thermal efficiency of a gas-turbine plant it is expedient to introduce multistage combustion and multistage cooling of the compressed working medium. The T-s diagram of such a cycle with a great number of stages is shown in Fig. 10.31. Such gas-turbine plants are operated as open-cycle installations with a rather high efficiency.

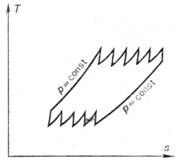
Fig. 10.31

In conclusion we shall again emphasize that our analysis of the effectiveness of the cycles of gas-turbine plants was based on the assumption that these cycles are reversible and that the working medium is an ideal gas whose heat capacity is independent of temperature. In considering actual gas-turbine plants and reciprocating internal-combustion engines, cycles should be analyzed taking into account the losses due to irreversibility, in particular by introducing the concept of the relative internal efficiencies of a plant.

---

[1] One may ask why, in considering piston-type internal combustion engines, do we assume the process of exhaust to be isochoric, and assume the same process to be isobaric when a gas turbine is involved? In fact, the reciprocating engine is a periodic-action machine (i.e. the properties of the working medium at a fixed point vary with time), and the turbine is a continuous-action machine (in steady-state operation the properties of the working medium do not change with time). It follows that at the turbine exit the exhaust pressure is always constant (p₄ = const) and close to atmospheric, whereas in a reciprocating engine, when the exhaust valve opens, the cylinder pressure drops to atmospheric pressure almost instantaneously, in a time interval during which the piston displacement is very small (v = const).

[2] It was shown in Sec. 7.9 that the only way of ensuring a compressed air temperature equal to the compressor inlet temperature is by multistage compression with intermediate cooling of the compressed gas in special heat exchangers.

[3] Considering the dependence plotted in Fig. 10.15, we should bear in mind that at ρ > 3 the pressure ratios β obtained are so high that they cannot be realized in practice. Consequently, for these values of ρ this dependence is of limited interest.

[4] The term "maximum, or limiting, regeneration", as distinct from the term "complete regeneration" considered for the cycle with isothermal expansion, was introduced to emphasize that during a cycle with adiabatic compression not all the heat contained in the exhaust gases is transferred to the air in the regenerator even at T₃ = T₅

(since T₁ < T₂). A fraction of that heat, represented in Fig. 10.25 by area a-1-6-c-a, is the heat q₂ transferred to the low-temperature source; but in the cycle with isothermal compression, q₂ is the heat transferred in the process of air compression.

[5] The values of the adiabatic (isentropic) exponent k for ideal gases were given in Sec. 7.4.