10.3 Reaction-engine cycles

A reaction engine is a device in which the chemical energy of fuel is converted into the kinetic energy of the jet propulsion of a working medium (gas) expanding in the nozzles. This jet creates thrust because of the reactive, or back action, of the working medium, flowing from the engine backwards relative to aircraft motion.

If we denote by G_gas the mass of gas flowing from the exit nozzle of a reaction engine in some time interval , and use w_gas to denote the velocity of this gas relative to the flying vehicle (jet-propelled aircraft or rocket) and F to denote the thrust of the reaction engine, then in accordance with Newton's second law,

(10.79)

we obtain for the moving vehicle (taking into account that the velocity with which the gas flows from the nozzle changes from a relatively low velocity in the combustion chamber to w_gas at the nozzle exit, i.e. ):

(10.80)

or, introducing the notation g_gas = G_gas/ (the rate of gas flow),

(10.81)

Reaction engines are divided into two main categories, rocket engines and jet engines.

Rockets carry both fuel and an oxidizer required to ensure fuel combustion (liquid oxygen, ozone, hydrogen peroxide, nitric acid, etc.). Unlike rocket engines, jet engines carry only fuel, and atmospheric air is used as an oxidizer. Hence, jet engines are only suitable for operation in the Earth's atmosphere, whereas rocket engines are capable of service both in the atmosphere and in space.

Let us first consider the cycles of jet engines. Air-breathing engines are divided into turbojet and compressorless engines according to the principle of operation.

The schematic diagram of a turbojet is shown in Fig. 10.32. In this type of engine the liquid fuel, delivered from the fuel tanks, burns in the combustion chamber 1. The products of combustion, upon expansion in the nozzle 2, are then discharged into the surroundings. Air oxygen is the oxidizer for fuel combustion. The thermal efficiency of this engine is increased by introducing precompressed air. This air, drawn from the atmosphere through diffuser 3, is compressed in an axial or centrifugal compressor 4 from which it is discharged into the combustion chamber. The compressor is driven from a special gas turbine 5 which is run by a portion of the products of combustion as they pass through it; the products of combustion then expand in the propelling nozzle.

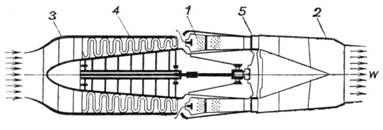
Fig. 10.32

It follows that the cycle of a turbojet engine is realized as follows (p-v diagram in Fig. 10.33). Air is compressed in the turbocompressor[1] from atmospheric pressure p₁ to pressure p₂ along adiabat 1-2. Then the heat released upon fuel combustion, q₁, is added to the working medium, this process proceeding under a constant pressure (isobar 2-3). The working medium (compressed air + products of combustion) expands first in the gas turbine, and then in the propelling (jet) nozzle 3 of the engine along adiabat 3-4 (from point 3 to point b doing work in the gas turbine, and from point b to point 4 accelerating the flow in the nozzle). The cycle is closed by isobar 4-1 at atmospheric pressure.

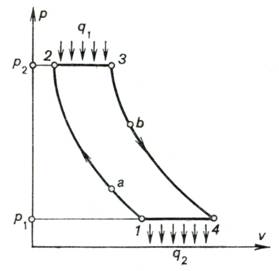
Fig. 10.33

We see that the cycle of a turbojet engine does not differ from the cycle of a gas-turbine plant where combustion proceeds at p = const (see Sec. 10.2). Hence, the relationships previously derived are applicable to the turbojet cycle. At the present time turbojet engines are the basic type of engine for high-speed aircraft.

We now turn to the compressorless jet engines. Here there is no compressor, as the name implies, and compression of air is due to the conversion of the kinetic energy of the atmospheric air moving backwards relative to the aircraft, known as the ram effect.

Compressorless jet engines are divided into two groups: the ramjet and the pulsejet.

The schematic layout of a ramjet is shown in Fig. 10.34. There is no compressor or turbine in this engine. Atmospheric air is compressed in diffuser 1 from atmospheric pressure p₁ to p₂ and flows into combustion chamber 2 into which liquid fuel is injected. Combustion proceeds at a practically constant pressure (p₂ = const). The products of combustion, which are at a high temperature, discharge from the propelling nozzle 3.

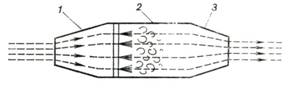
Fig. 10.34

Thus, the cycle of a ramjet (shown on the p-v diagram in Fig. 10.35) consists of an adiabat representing compression of atmospheric air in the diffuser (process 1-2), an isobar showing the process of fuel combustion (process 2-3), an adiabat of air expansion in the propelling nozzle (process 3-4), and the cycle closing isobar representing cooling of the products of combustion at atmospheric pressure (process 4-1). The cycle of a ramjet is thermodynamically similar to that of a constant-pressure combustion gas turbine and also to the cycle of a turbojet. In accordance with Eq. (10.53), the thermal efficiency of this cycle will be the higher the greater the pressure ratio

β = p₂/p₁ (i.e. the higher the speed of the aircraft with the ramjet), which determines the dynamic pressure (head) of the stream of air, turning, as the air is decelerated in the diffuser, into static pressure. The thermal efficiency of a ramjet, consequently, increases with aircraft speed.

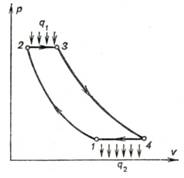
Fig. 10.35

The dependence of the thermal efficiency of a ramjet cycle on aircraft speed (or, on the velocity of air relative to the aircraft) can be derived as follows.

Equation (10.53) for the thermal efficiency of a constant-pressure combustion gas engine (adiabatic air compression),

and Eq. (10.51) for adiabatic air compression,

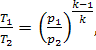
yield that for this cycle

(10.82)

where T₁ is the air temperature before compression, and T₂ the air temperature at the end of adiabatic compression.

If we denote the velocity of air relative to the aircraft (i.e. aircraft velocity) by w₁ and the velocity of air flowing into the combustion chamber by w₂, then, in accordance with the equation derived in Chapter 8, Eq. (8.8), we find that

where i₁ and i₂ are the enthalpies of air before adiabatic compression (i.e. at the inlet of the ramjet diffuser) and after adiabatic compression (at the diffuser exit, i.e. at the inlet of the combustion chamber of the ramjet).

Assuming, as before, air to be an ideal gas with a constant heat capacity, for which

(10.83)

we obtain from Eq. (8.8):

(10.84)

Thus,

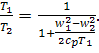(10.85)

Substituting the above expression into Eq. (10.82), we obtain the following relation for the thermal efficiency of a ramjet cycle:

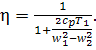(10.86)

Ignoring the velocity in the combustion chamber , we get

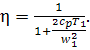(10.87)

The dependence of the thermal efficiency of a ramjet engine on flight speed, calculated from Eq. (10.87), is represented graphically in Fig. 10.36.

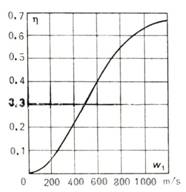
Fig. 10.36

It will be noted that from Eqs. (10.51) and (10.85) it follows that the dependence of the pressure ratio β = p₂/p₁ on flight speed is determined from the relationship

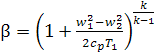(10.88)

Ramjets intended for subsonic and supersonic speeds should naturally be constructed differently. The schematic diagram of the ramjet, shown in Fig. 10.34, corresponds to subsonic speeds. It will be recalled that, as it was shown in Sec. 8.4, a subsonic stream is decelerated in a diverging nozzle, and the flow is accelerated in a converging nozzle; this kind of nozzle and diffuser are illustrated in Fig. 10.34. A ramjet for supersonic speeds is shown schematically in Fig. 10.37. To be suitable for such flight conditions, the diffuser must have a converging section in which the supersonic flow is decelerated to sonic velocity; further deceleration of the flow then takes place in the diverging subsonic diffuser.

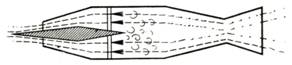
Fig. 10.37

It ought to be mentioned, however, that, as is known from gas dynamics, the deceleration of a supersonic flow in a converging duct is accompanied by a number of shock waves inside the duct, which cause important losses in flow energy, a considerable deviation of the compression curve from an isentrop and a drop in the pressure ratio. In order to avoid this, diffusers are fitted with a sharp cone facing the flow which ensures a gas-dynamical rearrangement of flow from supersonic to subsonic upstream from the diffuser inlet. Thus, there is no need to fit a converging section (cone) in front of the diffuser. It is clear that the nozzle is made in the shape of a supersonic Laval nozzle.

Under subsonic conditions (take-off and landing) the diverging part of the Laval nozzle and diffuser cone are idle and serve no purpose; the engine acts as a subsonic plant whose schematic diagram is shown in Fig. 10.34.

With a flying speed equal to zero (aircraft take-off) the pressure ratio ensured by a ramjet is one, its thermal efficiency is zero, and the engine will fail to perform. Ramjet-powered aircraft are, therefore, fitted with special launching boosters to impart an initial speed.

These peculiarities of ramjets and their simple construction, small weight and size make this type of engine ideal for aeroplanes intended for high supersonic speeds.

The pulsejet whose performance cycle is shown in Fig. 10.38 on a p-v diagram, is fitted with a special valve-type device ensuring isolation of the combustion chamber from the diffuser and nozzle, so that the process of combustion proceeds at a constant volume. Periodic action characterizes this engine and gives it its name, the pulsejet. The cycle of a pulsejet is similar to the cycle of the constant-volume combustion gas turbine, previously studied.

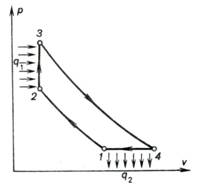
Fig. 10.38

As was shown in the preceding section, for the same pressure ratios and the same temperatures at the end of the process of expansion and with adiabatic air compression, the thermal efficiency of a constant-volume combustion cycle is higher than that of a constant-pressure combustion cycle.

Because of their intricate construction, the pulsejet have not yet found wide application.

Let us now examine the cycles of rocket engines.

Rocket engines are divided into chemical rocket engines and nuclear rocket engines.

Chemical rocket engines are divided, in turn, into two main groups: solid propellant rocket engines and liquid propellant rocket engines. In a solid propellant rocket engine, the solid fuel (usually powders of various kinds), containing both combustible substances and an oxidizer, takes fire when the rocket is being launched and burns out gradually, forming gaseous products of combustion which discharge from the nozzle. The schematic diagram of a solid propellant rocket engine is illustrated in Fig. 10.39, showing combustion chamber 1, solid propellant 2 and nozzle 3.

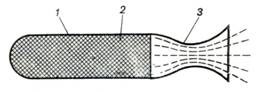
Fig. 10.39

An ideal cycle of a solid propellant rocket engine is shown on the p-v diagram in Fig. 10.40. When the engine is started, the pressure of the gaseous products of solid propellant combustion increases instantaneously from atmospheric pressure p₁ to some pressure p₂. In different types of engines, the magnitude of the pressure p₂ may reach tens and even hundreds of atmospheres; the pressure rises at so high a rate that this process may be considered as isochoric (line 1-2).

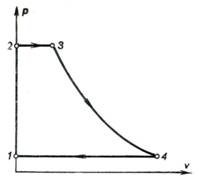
Fig. 10.40

It may be assumed that heat is added to the products of combustion isobarically (line 2-3). The gaseous products of combustion then expand adiabatically in the nozzle (line 3-4). The cycle is closed by isobar 4-1 representing the cooling of the products of combustion in the surrounding medium. In the combustion chamber, the density of the solid propellant products of combustion is so high compared with that of the gases leaving the nozzle that in Fig. 10.40 isochor 1-2 is depicted coinciding with the vertical axis.

Due to their simple design and convenient handling in operation, solid propellant rocket engines find an ever growing application in rocketry.

A schematic diagram of a liquid propellant rocket engine is presented in Fig. 10.41. The liquid propellant and the oxidizer are delivered into combustion chamber 1 from propellant tank 2 and oxidant tank 3 with the aid of pumps 4 and 5. Combustion proceeds at a practically constant pressure p₂. The gaseous products of combustion flow through and discharge from the nozzle into the surroundings.

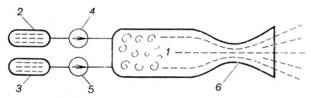
Fig. 10.41

The ideal cycle of a liquid propellant rocket engine is plotted on the p-v diagram shown in Fig. 10.42.

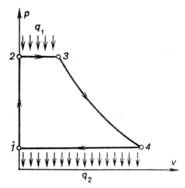
Fig. 10.42

The liquid propellant and oxidizer (or oxidant) are delivered into the combustion chamber at a pressure p₂. Therefore, in a liquid propellant rocket engine, not a gaseous working medium is compressed, as in a solid propellant engine, but the individual liquid components of this working medium. Inasmuch as liquid can be considered virtually incompressible, the compression of the components of the combustible mixture can be assumed to be isochoric. Since the density of liquid is much greater than that of the combustion products, in Fig. 10.42 the isochor 1-2 is plotted as practically coinciding with the vertical axis. The isobar 2-3 corresponds to the process of heat addition in the combustion chamber, and adiabat 3-4 represents expansion in the propelling nozzle. Isobar 4-1 (surroundings pressure) closes the cycle.

Thus, in principle, the cycle of a liquid propellant rocket engine is similar to the cycle of a solid propellant rocket engine.

The thermal efficiency of the ideal cycle of a liquid propellant rocket engine can be calculated as follows.

The amount of heat q₁ added during the isobaric process 2-3 is

(10.89)

It should be emphasized here that, as above, we consider the products of combustion to be an ideal gas with a constant heat capacity; the amount of heat q₁ however, can not be calculated from formula (10.13),

since the components of the combustible mixture enters the combustion chamber at a temperature T₂ in the liquid state, then evaporate and react chemically. Thus, on the isobar 2-3 the working medium changes phase; therefore the amount of heat q₁ should be calculated with the aid of the more general Eq. (10.89), instead of formula (10.13), to account for any transformation of the substance of this isobar.

The quantity q₂ can be presented in the form

(10.90)

The general expression for the thermal efficiency of the cycle,

taking into account Eqs. (10.89) and (10.90), takes the following form:

(10.91)

or, which is the same,

(10.92)

The difference in enthalpies (i₂ – i₁) is equivalent to the work expended by pumps 4 and 5 (Fig. 10.41) to raise the pressure of the liquid components of the combustible mixture during the isochoric process 1-2.[2] Inasmuch as the specific volumes of the liquid fuel (propellant) and oxidant are rather small, the work expended to ensure their compression is negligible compared with the amount of heat released upon combustion of the liquid propellant. The quantity (i₂ – i₁) present in Eq. (10.92) can, therefore, be ignored. With this in mind, Eq. (10.92) gives the following expression for the thermal efficiency of the cycle of a liquid propellant rocket engine:

(10.93)

Inasmuch as the difference in enthalpies (i₃ – i₄) converts into the kinetic energy of the products of combustion as they discharge from the nozzle, in accordance with Eq. (8.8), ignoring the speed of the products of combustion at the nozzle inlet, we can write

(10.94)

where w is the velocity with which the products of combustion leave the nozzle of a liquid propellant engine.

Taking into account relationship (10.94), Eq. (10.93) can be given the following form:

(10.95)

Liquid-propellant rocket engines find wide application in rocketry and very often in aeronautical engineering.

Let us now consider the cycles of nuclear rocket engines[3].

A possible design of a nuclear rocket engine is shown schematically in Fig. 10.43. The liquid working medium, contained in tank 1, is forced to flow by pump 2 through the core of nuclear reactor 3. In the nuclear reactor, heat is added to the working medium at a constant pressure. From the reactor the already gaseous working medium flows into nozzle 4 in which it expands and then discharges into the surroundings. It is clear that the cycle of a nuclear rocket engine is thermodynamically identical to the cycle of a liquid propellant rocket engine. Consequently, the thermal efficiency of the cycle realized in a nuclear rocket engine, just as that of a liquid propellant rocket engine, is determined by Eq. (10.95).

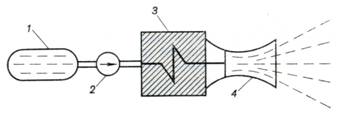
Fig. 10.43

Another possible design of a nuclear rocket engine is represented schematically in Fig. 10.44. The liquid working medium, containing the nuclear fuel (uranium-235 or plutonium) in the form of a suspension or of another mixture, is delivered from tanks 1, fitted with special devices that prevent a chain reaction, into "combustion" chamber 2, where the mass of the nuclear fuel exceeds the critical mass and a chain reaction begins. The heat released during the nuclear reaction heats the working medium, which then expands in nozzle 3 and discharges into the surrounding medium. The cycle of this nuclear rocket engine is thermodynamically similar to the preceding one.

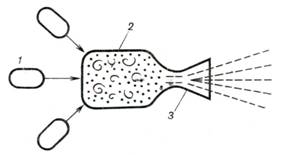
Fig. 10.44

It should be noted that as distinct from jet engines and rocket engines with a chemical propellant, the working medium of nuclear jet engines is not a product of fuel combustion. This means that for a nuclear rocket engine the working medium can be chosen on the basis of maximum thermodynamic expediency.

From Eq. (8.29) for the velocity of flow of an ideal gas through a nozzle[4], we obtain for the case of flow into an evacuated space (the pressure in outer space can be considered virtually zero), i.e. for p₂ = 0[5] we have:

(10.96)

or, which is the same,

(10.97)

Since the quantity is constant, it follows from relationship (10.97) that maximum velocities of flow through a nozzle are ensured when gases with a small molecular weight μ are used. From this point of view the most advantageous working medium for a nuclear-powered, or nuclear, rocket is hydrogen H₂ (μ = 2), which at the high temperatures in the "combustion" chamber of the nuclear reactor dissociates into atomic hydrogen (μ = 1).

Besides hydrogen, helium, water vapour (steam) and hydrogen compounds of light elements are possible working media for nuclear rocket engines.

We must note that although the thrust of nuclear rocket engines is small compared with the thrust of liquid (or solid) propellant rocket engines, a nuclear engine is capable of operating for a considerably longer time (several orders of magnitude longer) than a rocket engine firing a chemical (liquid or solid) propellant. Nuclear rockets, therefore, are the most suitable type of engine for manned interplanetary spaceflights. It appears that a spaceship should be launched from the Earth with the aid of liquid or solid propellant engines, with a nuclear rocket engine used for flying in space outside the Earth's gravity.

---

[1] When a jet-propelled aircraft flies at high speeds, partial compression of the air takes place in the diffuser, due to stagnation (braking) of the free-stream flow of air in the diffuser.

[2] It is clear that

and

where the indices "prop" and "oxid" refer to the propellant and oxidant, respectively, and g is the mass fraction of the propellant in the combustible mixture.

[3] Until now a nuclear rocket engine has not been built, but the possibility is widely discussed in the literature.

[4] It will be recalled that this equation is applicable for any values of (p₂/p₁) if the gas flows through a Laval nozzle.

[5] For adiabatic discharge in an evacuated space (back pressure p₂ = 0) it follows from Eq. (7.61) that T₂ = 0 K, i.e. at the nozzle exit the gases are at the absolute zero temperature. This means that the entire enthalpy of the gas turns into the kinetic energy of gas flow.