11.6 Binary cycles
On the basis of our
analysis of steam power cycles we can formulate the requirements which the
most thermodynamically and operationally convenient working medium is expected
to meet. These requirements are as follows:
(1)
The working medium must
ensure as high a cycle area ratio as possible. For this purpose it must have
as low an isobaric (constant-pressure) heat capacity in the liquid state as
possible (in this case the isobars, whose slope is determined by the quantity 
will run quite steep on the diagram approaching the
vertical). It is also desirable that the working medium possess highest
possible critical parameters, or conditions; at the same vapour saturation
temperature a higher cycle area ratio is characteristic of the cycle realized
with a working medium at higher critical parameters.
(2)
The properties of the
working medium should be such that with a sufficiently high cycle area ratio
the high upper cycle temperature is ensured at not a very high vapour pressure,
i.e. that a high thermal efficiency is ensured without passing to excessively
high pressures. This makes plant construction more complicated. On the other
hand, the working medium should be such that its saturation pressure at the
lowest cycle temperature (i.e. at the temperature close to that of the
surroundings) is not too low; an excessively low saturation pressure will
require a high vacuum to be maintained in the condenser, involving great
technical difficulties.
(3)
The working medium must be
cheap; it should not chemically attack the construction materials used to build
the power plant; it should not be harmful to the attending personnel, i.e., it
should not be toxic.
Unfortunately, at the
present time no working medium is known that would meet all these requirements
completely. The working medium most widely used in modern heat-and-power
engineering, water, does not have a sufficiently low heat capacity in the
liquid state, but it satisfies the need for a not too low pressure in the
condenser; water is a rather suitable working medium for the low-temperature
processes of a cycle. However, operation of power plants with high steam cycle
area ratios, involves the use of high pressures; in this case, due to the
comparatively low critical temperature of water, when passing to high
pressures, the length of the isobaric-isothermal section of the two-phase
region diminishes. This decreases the rate at which the cycle area ratio
increases when passing to high pressures. It is precisely due to this that the mean
heat-addition temperature is comparatively low in a steam power cycle. This, as
was shown in Sec. 11.3, leads to considerable availability losses.
Other working media have
other shortcomings. For example, mercury has a low saturation pressure at high
temperatures and high critical parameters: pcr = 151 MPa (1540
kgf/cm2) and
Tcr = 1490 °C. At a temperature
of 550 °C, for instance, the saturation pressure of mercury is only 1420 kPa
(14.5 kgf/cm2). This permits the Rankine cycle to be realized with
saturated mercury vapour without superheating, ensuring a sufficiently high
thermal efficiency. On the other hand, at temperatures close to the temperature
of the surroundings the saturation pressure of mercury is too low: for T = 30
°C we find that 
0.36 Pa (
kgf/cm2),
while for the pressure usually maintained in the condensers of steam turbines [
4 kPa (0.04 kgf/cm2)] there is an
excessively high mercury saturation temperature, 
= 217.1°C. The thermal efficiency of a cycle
realized with so high a lower cycle temperature would be low. Thus, mercury is
suitable as a working medium for the upper (high-temperature) part of a cycle
but cannot be used to realize its lower part.
Since at the present time
no working medium is known that would meet the above requirements throughout
the entire temperature interval of a cycle, it is possible to realize a cycle
with two working fluids, using each in the temperature interval in which the
working medium has the greatest advantages.
Cycles of this kind are
referred to as binary cycles. The schematic diagram of a heat power
plant operated on a mercury-water cycle is shown in Fig. 11.31.
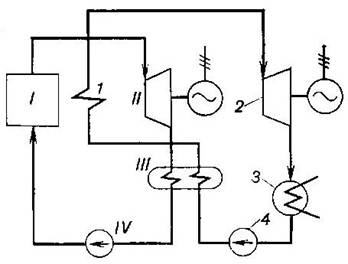
Fig. 11.31
In the mercury boiler I heat
is added to the mercury, the mercury evaporates and dry saturated mercury
vapour flows at a pressure 
into the mercury
turbine II where the mercury vapour
does work transferred to the electric generator coupled with the turbine. From
the turbine the waste mercury vapour, which is at a pressure 
is sent into the condenser-evaporator III, where it condenses. Pump IV then delivers the liquid mercury
into boiler I raising the mercury
pressure from to .
The condenser-evaporator is
a surface-type heat exchanger in which heat is transferred from the condensing
mercury vapour to the cooling water. This heat heats the cooling water in the
condenser-evaporator to the boiling point, and the water evaporates. From the
condenser-evaporator the dry saturated water vapour, steam, is sent into
superheater 1, usually arranged in the gas flue of the mercury boiler.
The superheated steam flows at a pressure of 
into steam turbine 2 coupled with an
electric generator. The pressure of exhaust steam is 
and it condenses in condenser 3; pump 4 then delivers the water (condensate) into the
condenser-evaporator.
It should be noted that the
rates of working medium flow in the mercury and steam-generating circuits differ.
The relation between the rate of flow of mercury and the rate of flow of water
through their respective circuits is determined on the basis of the following
considerations. Let us consider, for instance, a binary vapour cycle in which
the mercury cycle is realized with dry saturated mercury vapour in the pressure
interval of = 1180 kPa = 12 kgf/cm2 (at that pressure
the mercury saturation temperature is 
= 532.1 °C) and = 9.8 kPa = 0.1 kgf/cm2 (the saturation
temperature 
= 250 °C), and the initial parameters of steam in
the water-vapour cycle are = 3330 kPa = 34 kgf/cm2 (Ts = 239.8 °C[1])
and T1 =
400 °C at the lower pressure 
= 4 kPa = 0.04 kgf/cm2.
At a pressure of 0.1 kgf/cm2
the latent heat of vapourization of mercury, rM = 299.0 kJ/kg (71.42 kcal/kg), and the difference
between the enthalpies of dry saturated water vapour (steam) and water at a
temperature of 28.6 °C on the isobar with 3330 kPa (i.e. the total amount of
heat required to heat the water leaving the condenser to the boiling point and
then to evaporate it) is equal to 2680 kJ/kg (640 kcal/kg). It is clear that to
heat 1 kg of water to the boiling point in the condenser-evaporator and then
evaporate it, heat must be rejected (transferred) from 640/71.42 = 8.95 kg of
the condensing mercury vapour. Thus, the rate of working medium flow in the
mercury circuit of a binary plant must be 8.95 times the rate of working
medium flow in the steam-generating circuit of this plant. In the general case,
this ratio of the mercury and water rates of flow, m, is determined from
the relation
(11.126)
where 
is the
efficiency of the condenser-evaporator, accounting for the heat losses in this
device.
The T-s diagram of
this binary vapour cycle is shown in Fig. 11.32. This diagram is plotted for 1
kg of water and 8.95 kg of mercury, assuming the cycle to be internally
reversible. The steam generating part of the cycle is an ordinary Rankine cycle
realized with superheated steam. The mercury part above the steam-generating
cycle is a Rankine cycle realized with wet vapour. Here ab represents
the adiabatic process in the mercury turbine, bc the heat transfer from
the condensing mercury vapour, cd the process proceeding in the mercury
pump, and dea shows the isobaric process of adding heat to the mercury
in the mercury boiler.
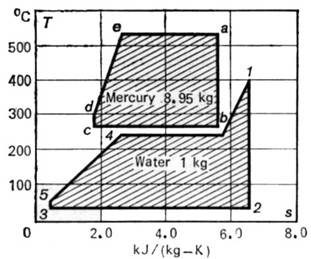
Fig. 11.32
The reader may be puzzled,
since it was mentioned above that when water vapour (steam) is used as a
working medium, the Rankine cycle without superheating is usually not practised
due to the fact that at the end of the process of expansion in the turbine the
wetness of the expanding steam is very high, reducing sharply the internal
relative efficiency of the turbine. But then why can the mercury cycle without
superheating be used without any reservations? In fact, on the T-s diagram
for mercury the right boundary curve runs much steeper than that plotted for
water. Owing to this, the state of the waste mercury vapour at the exit of the
mercury turbine happens to be located in the wet vapour region, close to the
right boundary curve, i.e. in the zone of high dryness fractions.
The thermal efficiency of
the binary vapour cycle is determined from the expression
(11.127)
where 
and 
are the amounts of work performed in the mercury
and water-vapour parts of the binary cycle and and 
are the amounts of heat added in the mercury and
water-vapour parts of the binary cycle. The values of l and q1 are usually given per
kilogram of the working medium, and the difference between the amounts of the
working medium used in the mercury and water-vapour parts of the cycle is
accounted for by the ratio of mercury and water, m. It must be
emphasized that in the binary vapour cycle 
is the heat which is expended to superheat the
water vapour, or steam, i.e. = i1 — i6 (inasmuch as the water is heated to the boiling
point and then evaporated at the expense of the heat released by the condensing
mercury vapour).
In the binary vapour cycle
considered,
kJ/kg (277.0 kcal/kg),
kJ/kg (70.9 kcal/kg),
kJ/kg (26.3 kcal/kg),
kJ/kg
(78.7 kcal/kg).
Allowing for m =
8.95, Eq. (11.127) gives:
For comparison let us
calculate the thermal efficiencies of the upper mercury and lower water-vapour
cycles of the binary vapour cycle:
(in this case 
kJ/kg) and
In this way, the use of the
mercury cycle on top of the water-vapour cycle permits an important increase of
the cycle thermal efficiency.
In addition to mercury,
diphenyloxide (C6H5)2O, a diphenyl mixture
(75% diphenyloxide and 25% diphenyl C12H10), antimony
bromide SbBr3, silicon bromide SiBr4, aluminium bromide
Al2Brs and other substances are suggested for use as
working media in the upper cycle of the binary vapour cycle.
It should be noted,
however, that up till now binary vapour cycles have not been widely used[2],
chiefly because of the technical difficulties involved in erecting such plants.