2.3 Internal energy and external
work
Let us consider the process of adding heat
from the outside, or from some heat source, to some body whose volume is
maintained constant (for instance, to a gas kept in a vessel of constant
volume). As it is generally known from experience, the addition of heat to a body
results in a rise in its temperature.
In accordance with the law of conservation
and conversion of energy, the heat added to a body corresponds to the increase
of its internal energy. The latter, denoted by U, is the sum of the
energies due to the translational and rotational motion of molecules of a body,
the energy of intermolecular oscillations, the potential energy of
intermolecular adhesion forces, intermolecular energy, nuclear (the energy of
the atomic electron shells) and intranuclear energy.
The process of adding heat to a body was
considered above as taking place in a way so that the volume of the body
remains constant. It is common knowledge that in the general case bodies
usually will expand upon heating. Consequently, in the general case the volume
of a body will increase upon heating. If the body considered is placed in
surroundings under a pressure pm, then, as the volume of the body increases, work
will be accomplished against the forces of external pressure pm. Indeed, let us
consider the increase in volume V of a body of arbitrary shape placed in
surroundings under a pressure pm (Fig.
2.2). The area of the surfaces of the body shall be denoted by F. If the
change in the volume of the body is considered to be an infinitesimal, dV, this increase in volume can be
visualized as the displacement of each point of the surface of this body
through a distance dx, Since
pressure is the force exerted normal to a unit area of the body, it is obvious
that the sum of the forces acting upon the entire surface of the body will be P
= pmF.
The work done to shift the surface F of the body through a distance dx,
not withstanding the counteraction offered by the external pressure, is
dL
= pmF dx, (2.2)
and since
F
dx = dV, (2.3)
we get:
dL
= pm dV. (2.4)
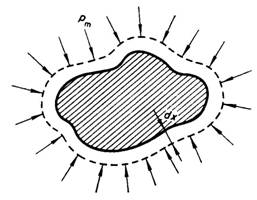
Fig. 2.2
It follows from Eq. (2.4) that with a finite change in
volume,
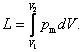(2.5)
The work L done
against the forces of external pressure and associated with the change in the
volume of a system is called the work of expansion done by the system on
the surroundings.
It should be emphasized that the work of expansion against the forces of
external pressure is done only when the body involved undergoes a change in
volume V (and when the external pressure is not zero). Below in the book
we shall deal mainly with processes in equilibrium for which the equality pm = p is true. So, unless otherwise specified, for the
work of expansion we shall use the following relationships
dL
= p dV (2.4a)
and
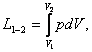(2.5a)
derived from (2.4) and (2.5), substituting p for
pm.
It is convenient to calculate the work of
expansion determined by Eq. (2.5a) with the aid of the p-V diagram. Let us see
how the process involving a change in the volume of a system is represented on
this diagram (Fig. 2.3). The volume of the system changes from V1 to V2. The
states that the system undergoes in the process of expansion are located on the
curve, or path, of the process, between points 1 and 2. It is clear from Eq. (2.5a) that
the work done by the expanding system is represented on the p-V diagram by the shaded area
below the path of the process (Fig. 2.3).
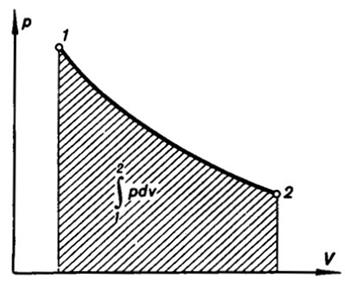
Fig. 2.3
It should be stressed that the magnitude
of the work of expansion accomplished by a system, expanding from the state
with volume V1
to the state with volume V2, depends
not only on the properties of these states but also on the path of the process
of expansion. Indeed, as can be seen from the p-V diagram depicted in Fig. 2.4, the magnitude of the
integral
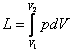
will be different, depending on the path (A, B or
C) of the process of expansion. Thus, the work of expansion is a
function of the process.
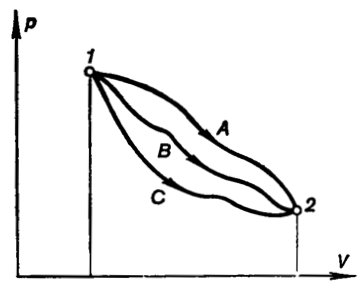
Fig. 2.4
It will also be recalled that in mechanics
the work performed by some arbitrary force F is the name given to the integral
(2.6)
where 
is the projection of
force F on the direction of the elementary
displacement of the body, dx (or, more accurately, of the coordinate
characterizing the position of the body), acted upon by this force.
It is clear that for the work of expansion
(2.5) is a particular case of (2.6). In the general case, in addition to the
work of expansion, a body is capable of performing other kinds of work, for
instance, the work spent to increase the surface of the body overcoming the
forces of surface tension, the work involved in displacing the body in a
gravitational, electric or magnetic field, etc. The work calculation formulas
for all these cases will be of a similar structure, like Eq. (2.6), i.e.
dL = y dY (2.7)
and correspondingly
(2.8)
where y is the external force acting upon the
body (system), and Y the property of state (coordinate) of the system
associated with the force y.
The force y is known as the generalized force, and Y is referred to
as the generalized coordinate.
If a system is acted upon simultaneously by several different forces,
the work performed by this system will be equal to the sum of the works done by
the system due to each of the acting forces
(2.9)
and
(2.10)
where yi is the generalized force, Yi
the generalized coordinate associated with the ith force, and n the number of generalized
forces.
It is clear that in the general case when
the system performs only work of expansion, n = 1, yi = p, Yi = V. But if, for instance, the height z
to which a body of mass G is elevated changes, i.e. if the potential
energy of the body in the gravitational field changes, then, as it is known
from mechanics, work is being done against the gravity of the body Gg. For this case, obviously, yi
= Gg, Yi = z and, in
accordance with Eqs. (2.9) and (2.10) and allowing for G = const, we
have
dL = Gg dz (2.11)
and
(2.12)
Since below we shall mainly consider
systems which perform only work of expansion against forces of external
pressure, any kind of work shall be denoted by L, and any kind of work, except the work of expansion, by L*. Then
dL
= p dV + dL* (2.13)
and
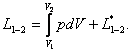(2.14)
Equations (2.13) and (2.14) are written
for a system whose mass is G. For a unit mass (1 kg, 1 g, etc.) these
equations take the form
dl
= p dv + dl*; (2.13a)
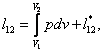
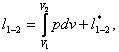(2.14a)
where l is the work per a unit mass of
the substance.