2.4 Mathematical statement of the first law of
thermodynamics
In the general case, when the addition of
heat to a body results in a rise in the temperature of the body, and external
work is performed due to an increase in the volume of the body, the heat added
to the body is expended to increase its internal energy U and to
accomplish work L. This statement can be expressed by the formula
Q1-2 = ΔU1-2 + L1-2, (2.15)
where Q1-2 is the heat added to the body while heating it from state 1 to
state 2; ΔU1-2
the change in the internal energy of the body during the same process
equal, as it will be shown below, to the difference between the internal
energies of the system at points 2 and 1; and L1-2
the work done by the body in the process 1 → 2.
Equation (2.15) is the mathematical expression of the first law of
thermodynamics, which is a particular case of the more general law of
conservation of energy.
When expressed in differential form, the same relationship takes the
following appearance:
dQ
= dU + dL. (2.16)
Below, the heat added to a system will be
considered as positive, and the heat removed, or rejected, from the system, as
negative. Accordingly, the work done by a system will be referred to as
positive, and the work done on a system as negative. It is clear that the
choice of sign is absolutely arbitrary, an opposite system of signs could be
chosen just as well. It is only necessary to observe a uniformity in all
further thermodynamic reasonings and calculations.
In the preceding paragraph, the work of
expansion has been shown to depend on the path of the process of expansion,
i.e. to be a function of the process. It can be easily shown that the heat
added to the system is also a function of the process, since the amount of
added heat depends on the amount of work done.
As to the internal energy of the body
(system), for a given body its magnitude depends only on the state of the body.
This point follows from the law of conservation of energy and is independent on
how true are our ideas about the microstructure of matter.
The work expended in Joule's experiment
(Sec. 2.1) must, obviously, accumulate in the water filling the copper vessel
in the form of the intrinsic energy of the water, depending only on its state,
or on the internal energy of the water.
On the basis of the objectives of
engineering thermodynamics, there is no need to consider the nature of the
internal energy of a substance from the point of view of the microstructure of
the substance. It will only be recalled that according to modern ideas the
internal energy of a substance can be visualized as the sum of the kinetic and
potential energies of the molecules (atoms, ions, electrons) of this substance.
A fraction of the internal energy changes only as a result of chemical
transformations and must be accounted for only in processes accompanied by
chemical changes.
It follows from the foregoing that the
change in the internal energy of a body undergoing some process is independent
of the nature of the process and is determined unambiguously by the initial and
final states of the body.
With account taken of the fact that the
change in the internal energy in a thermodynamic process is equal to the
difference in internal energies at the initial and final states of the process,
i.e.
ΔU1-2 = U2 – U1,
the
equation expressing the first law of thermodynamics in the integral form (2.15)
can be represented as follows:
Q1-2 = (U2 – U1) + L1-2. (2.15a)
Internal energy is an extensive
property of substance, i.e. U is proportional to the amount of
substance G in the system. The quantity
(2.17)
called
the specific internal energy, is the internal energy of a unit mass of
substance.
For the sake of brevity, the specific weight internal energy u will
be referred to as internal energy, and the quantity U as the total
internal energy of the entire system.
If the mass G of the system remains
constant, with account taken of Eq. (2.17), the equation expressing the first
law of thermodynamics takes the following form:
q1-2 = (u2
– u1) + l1-2 (2.18)
and
dq
= du + dl, (2.19)
where q is the amount of heat added to (or
removed from) unit mass of substance (for instance, 1 kg or 1 g), and l the amount of work performed by a
unit mass of substance (or work done on this amount of substance).
With account taken of Eqs. (2.13a) and
(2.14a), the equations of the first law of thermodynamics take the form:
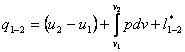(2.20)
and
dq
= du + pdv + dl*. (2.21)
For the case in which the only kind of
work done by the system is that of expansion, Eqs. (2.20) and (2.21) take the
form:
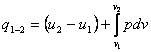(2.22)
and
dq
= du + pdv. (2.23)
For the entire system we can write
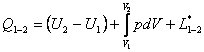(2.24)
and
dQ = dU+pdV+dL*; (2.25)
also
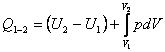(2.26)
and
dQ
= dU + p dV. (2.27)
Similar to a number of other thermodynamic
quantities, the internal energy is an additive quantity.
The name additive is given to quantities
whose magnitude for a system is equal to the sum of these quantities for each
of the components of the system. If we denote some thermodynamic quantity by Z,
then if this quantity is an additive one:
where the subscripts "sys" and i, respectively, refer to the
entire system and to its component (the number of the system's components is n).
Intensive quantities (such as pressure,
temperature) lack the property of additivity.
Internal energy is measured in the same
units as heat and work (Table 2.1).
The absolute value of internal energy is
essential for chemical thermodynamics in calculating chemical reactions, and we
shall return to it in Chapter 15. But in most engineering applications of
thermodynamics it is not the absolute magnitude of U that is of
importance but the change of this quantity in various thermodynamic processes.
From this it follows that for internal
energy the reference point can be chosen arbitrarily[1]. So, for instance, in
accordance with an international argument the reference point for water is
assumed to be the magnitude of internal energy at a temperature of 0.01 °C and
a pressure equal to 610.8 Pa = 0.006228 kgf/cm2 (the so-called triple
point).
In Chapter 1 it was stated that for a pure
substance any quantity which is a function of state is determined unambiguously
if any two other properties of the substance in this state are given. So, for
instance, the specific volume of a substance is determined unequivocally if
pressure p and temperature T are given. Analogously, internal
energy is a function of any two properties of state, and we can also write
u = f (v, T),
or
u
= φ (p, T),
or
u = ψ (p, v).
For a number of practical applications it
is most convenient, as it shall be shown below, to express internal energy as a
function of specific volume and temperature: u = f (v, T).
From integral calculus it is known that if
the magnitude of a line integral is independent of the path of integration and
is determined only by the initial and final points, or limits, of integration,
the integrand is a total differential. The total differential dz of a
function of two independent variables z = f (x, y) is the name given to the sum
(2.28)
The subscripts found at each of the
partial derivatives show that this derivative was taken assuming the subscript
to be constant.
Inasmuch as the line integral of any
function of state (including the function of u) is independent of the path of integration, the differential of
any function of state is a total differential. In particular, for internal
energy u = f (T, v) we can write
(2.29)
As for such functions of a process as heat
and work, it can be shown (see Sec. 4.1) that their differentials are not total
differentials. From this viewpoint the quantities dq and dl are
merely infinitesimal quantities of heat and work.
From the mathematical formulation of the
first law of thermodynamics, Eq. (2.23), applied to an isochoric process (dv = 0) it follows
that
dqv
= du, (2.30)
i.e. the heat added to a system undergoing an
isochoric process is only spent to change the internal energy of the system.
From this it follows that the expression for the constant-volume heat capacity cv
which, in accordance with Eq. (1.69), is expressed as
can take the following form:
(2.31)
This expression can be regarded as the
definition of the heat capacity cv. It shows that the heat
capacity cv characterizes the rate of growth of internal
energy u with temperature T in
an isochoric process.
It is clear that with account taken of
equation (2.31) the expression for the differential of internal energy (2.29)
takes the following form
(2.29a)
The partial derivative (𝜕u/𝜕v)T
characterizes the dependence of internal
energy of a substance on the specific volume v. The nature of this
dependence shall be elucidated in Chapter 4. Here we shall only consider the
nature of the dependence of internal energy on the specific volume for an ideal
gas.
In 1806 Gay-Lussac investigated
experimentally the dependence of the internal energy of a gas on volume. A
similar experiment was later repeated by Joule with a greater degree of
accuracy.
The outfit of Gay-Lussac—Joule's experiment is shown schematically in
Fig. 2.5. Two vessels (2 and
3), interconnected
by a pipe and cock 4, were
placed into thermostat 1, filled
with water and reliably heat insulated. Cock 4 was closed. Vessel 2 contained
a gas under a pressure pI,
and air was evacuated from vessel 3 (the pressure in the vessel pII ≅ 0). The pressure of the gas filling vessel 2, pI, was so low
that the gas could be considered to be an ideal gas obeying Clapeyron's
equation. Before the beginning of the test, the temperature of the water and
that of the vessels dipped in it had time to even out (denote this temperature
by t1). Then, cock 4 was
opened and part of the gas passed from vessel 2 into vessel 3, so that the pressure in the
two vessels evened out to some pressure p (it is clear that pI > p > pII). As a
result the temperature of the gas passing into vessel 3 somewhat
increased, and the temperature of the gas remaining in vessel 2 dropped.
However, in a rather short interval of time, due to the intensive heat transfer
between the vessels 2 and 3 and the water filling the thermostat,
a temperature equilibrium set in again over the entire volume of the
thermostat, with the temperature of the thermostat after the end of the
experiment, t2, being equal to the
thermostat temperature at the beginning of the test:
t1 = t2.
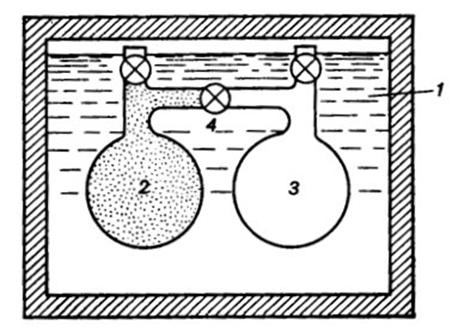
Fig. 2.5
Let us analyze the result obtained.
As was already mentioned, the system undergoing the test (thermostat
with water and the vessels dipped in the water) was ensured dependable heat
insulation and was of a sufficiently rigid construction (so that the volume of
the system would remain practically constant in the course of the experiment).
Consequently, there was neither heat nor external work exchange between the
system and the surroundings (dQ =
0 and dL = 0). Then, the equation of the first law of thermodynamics
(2.15a)
Q1-2 = (U2 – U1) + L1-2,
acquires
the following form:
U2 – U1
= 0
or
U2 = U1 (2.32)
i.e.
the experiment did not result in a change in the internal energy of the system
involved. Since internal energy possesses the property of additivity, the
internal energy of the system considered is the sum of the internal energies
of the gas in the two vessels, of the walls of the vessels, of the water filling
the thermostat and of the walls of the latter. Since t1 = t2, and the volume of the walls of the vessels, water and
of the walls of the thermostat did not change in the course of the experiment,
it is clear that the internal energy of these components of the system under
consideration did not change as a result of the experiment. Based on this, with
account taken of formula (2.32), we come to the conclusion that the internal
energy of the ideal gas investigated (denote it by Ug) did not change as a
result of the experiment:
As to the volume occupied by the gas, it changed substantially in the
course of the experiment: if before the experiment the entire gas was contained
in the volume of one vessel 2, after
the experiment was terminated the gas filled the volumes of the two vessels (2
and 3). Since the temperature of the
water after the test proved to be equal to that before the test was initiated and the internal energy underwent no change
in the experiment, it follows that the internal energy of an ideal gas is independent of volume:
(2.33)
or, which is the same,
(2.34)
This conclusion, known as Joule's law, is
of paramount importance. It reveals a new property of an ideal gas which does
not follow from its other properties, previously stated.
Since the pressure of the gas also changed
in the experiment and its temperature and internal energy remained constant,
together with relationships (2.33) and (2.34), for an ideal gas we can write
the following equations:
(2.35)
(2.36)
It should be noted that Eq. (2.35)
contains no new data on the properties of an ideal gas; it can be derived from
relationship (2.33) with the aid of the differential equations of thermodynamics
(see Chapter 4).
With account taken of Eq. (2.34), the
following equation can be derived for an ideal gas from Eq. (2.29a):
du
= cv
dT. (2.37)
The internal energy of an ideal gas
depends only on temperature.
As to real gases, the internal energy
depends not only on temperature, but also on volume. This, in particular, is
evidenced by the results of the tests conducted with the aid of the outfit
described above: when pressure pI of the gas in vessel 2 is considerable to
an extent that the gas can no more be considered to be an ideal gas, the
temperature of the gas t2
after the test was over differed from the temperature t1, i.e. t2 was less than t1. Hence, for a real gas
(2.38)