2.6 Mathematical statement of the first law of thermodynamics for processes of flow

Up till now we were considering only systems in which the substance did not move (as a whole) in space. It should be stressed, however, that the first law of thermodynamics is of a general nature and is true for any system, both fixed and moving.

Let us consider the flow of a liquid or gas in a conduit of arbitrary form. In considering the flow, one more factor should be taken into account, the kinetic energy of flow

(2.55)

where G is the mass of some fixed quantity of substance in the flow, and w is the flow velocity.

If the velocity of flow changes along the conduit between two sections (let us denote them 1 and 2, Fig. 2.6), the kinetic energy of the flow changes by

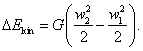(2.56)

Let us consider the equation of the first law of thermodynamics (2.15a):

Q_1-2 = (U₂ – U₁) + L_1-2.

Here the subscripts "1" and "2" are referred to the two sections of the flow (Fig. 2.6). Let us analyze the components of the quantity L_1-2, present in this equation, as applied to the flow; for this purpose let us investigate what kinds of work are performed by the flow of gas (or liquid).

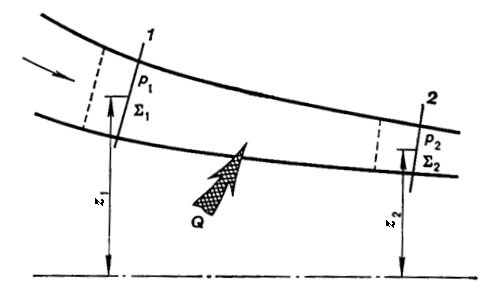
Fig. 2.6

So, consider the flow in a conduit of arbitrary form (Fig. 2.6). A certain amount of heat (Q₁₂ can be added to the flow between the sections 1 and 2.

Denote the cross-sectional area 1 of the conduit by Σ₁, and that of section 2 by Σ₂. The pressures under which the substance flows through the sections 1 and 2 are denoted, respectively, by p₁ and p₂.

The amount of substance passing through a section of the conduit per unit time (the mass flow rate) denote by G. It does not matter which of the two sections are chosen to measure the mass flow rate G; in accordance with the principle of continuity of flow, known from hydraulics, the mass flow rate of stationary flow is the same for any section of the conduit involved (G = const).

Let us determine the work performed by the flow.

In order to introduce a portion of the gas or liquid of mass G into the considered length of the conduit, through section 1 per unit time, it is necessary to spend a certain amount of work to displace a similar portion of the gas from the considered length of the passage, freeing, thereby, the space for the newly introduced portion of gas. Let us denote by x₁ the path covered by the portion of gas considered per unit time, as it passes through section Σ₁. For the sake of clarity, the section of this portion of gas can be visualized as moved by a piston without friction (inasmuch as in the general case the section of the conduit is variable, the fictitious piston should be of a variable cross-section; this assumption in no way effects the results obtained). In order to displace the piston by a distance x₁, an amount of work must be performed equal to the product of the force acting upon the piston (this force is equal to the product of gas pressure p₁ by the cross-sectional area of the piston Σ₁) by the length of piston travel per unit time:

L₍₁₎ = p₁ Σ₁x₁.

Denote

V₁ = x₁ Σ₁.

where V₁ is the volume of the gas passing into the part of the conduit considered per unit time. It is clear that

V₁ = v₁G,

where G is the mass flow rate through passage, and v₁ the specific volume of gas in section 1.

Thus,

L₍₁₎ = - p₁ v₁G. (2.57)

It should be noted that L₍₁₎ is the work done on the flow and, therefore, the quantity L₍₁₎ is negative [the "minus" in (2.57)].

The work done by the piston moving through section 2 is calculated in a similar manner

L₍₂₎ = p₂ V₂.

In accordance with the principle of continuity of flow formulated above, the mass rate of gas flow through section 2 is the same as through section 1; therefore,

V₂ = v₂G

and

L₍₂₎ = p₂V₂G. (2.58)

where L₍₂₎ is the work performed by the flow (piston 2) emerging from section 2. Consequently, this work is assumed to be positive.

It follows from Eqs. (2.57) and (2.58) that as the gas flows in a conduit from the arbitrarily chosen section 1 to section 2 at a mass flow rate equal to G, the work performed per unit time is equal to the algebraic sum of the work L₍₂₎ done by piston 2, and the work L₍₁₎ done on piston 1 (this work is called the work of displacement or transport work),

L_dis = L₍₁₎ + L₍₂₎,

whence, in accordance with (2.57) and (2.58), we have

L_dis = (p₂v₂ - p₁v₁) G. (2.59)

The work of displacement is the first component of the work done by the flow.

Further, if the flow velocity in section 2, w₂, differs from the flow velocity in section 1, w₁, then to change the kinetic energy of the flow, determined by Eq. (2.56), energy must be added (or removed):

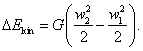
This is the second component of the work performed by the flow.

If the sections 1 and 2 are arranged at a different height (z₁ and z₂, respectively), work must be expended to elevate the considered portion of the gas from height z₁ to height z₂. This work is equal to the change in the potential energy of the portion of gas of mass G; in accordance with Eq. (2.12),

L_pot = Gg(z₂ – z₁).

This is the third component of the work done by the flow. In the general case the flow is also capable of performing other kinds of work as it passes from section 1 to section 2 of the conduit, for instance, rotate the wheel of a turbine or, if the flow of a conducting liquid in a cross magnetic field is involved, deliver electric power into an external circuit due to the magneto hydrodynamic effect, etc. All these kinds of work, referred to as mechanical work, we denote by L_mech. Mechanical work can not only be removed from a flow but also added to it: a flow can be delivered by a centrifugal pump, or handled by an electromagnetic pump, etc.

The mechanical work is the fourth component of the work performed by the flow.

Finally, the fifth component of the work of flow is the work spent to overcome skin friction between the flow and the walls of the conduit. Denote this kind of work by L_fr.

It follows that the work accomplished by a flow of gas (fluid or liquid) can be expressed in the general case by the following formula:

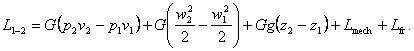(2.60)

Substituting the relationship for L₁₂ in the equation of the first law of thermodynamics (2.15a), we get:

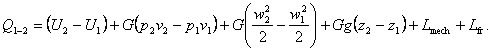(2.61)

Dividing both sides of Eq. (2.61) by G, we obtain a similar relationship for a unit mass of flow (i.e. expressed in specific quantities):

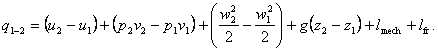(2.62)

In the differential form this equation becomes

(2.63)

Taking into account that

h = u + pv,

we get:

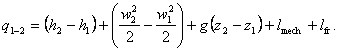(2.64)

and

dq = dh + wdw + gdz + dl_mech+ dl_fr. (2.65)

Equations (2.64) and (2.65) are the mathematical formulation of the first law of thermodynamics for a flow process.

Let us compare now the differential equation of the first law of thermodynamics, written in the most general form for an arbitrary system, with the private case of this equation for a flow process. The first of these equations, Eq. (2.23), is

dq = du + pdv,

and the second, Eq. (2.63),

dq = du +d(pv) + wdw + gdz + dl_mech+ dl_fr.

It should be borne in mind that Eq. (2.23) is written for the case when the only kind of work performed is expansion work. In this connection it should be stressed that the mechanical work accomplished by the flow, l_mech should not be confused with the work l*, present in Eq. (2.21), performed by the system on other, apart from pressure, generalized forces; when the velocity of flow is equal to zero, no mechanical work is performed, while the magnitude of l* does not depend on the velocity of the system (for instance, the work spent to overcome the resistance of surface tension while the surface is increasing).

It should be also stressed that in the case of frictional flow the work of the flow spent to overcome friction turns fully into heat transferred to the flow. Therefore, for the case of frictional flow, the quantity q in the left-hand side of Eqs. (2.23) and (2.63), represents the sum of the heat added to the flow from an outside source (denoted by q_ext) and the frictional heat q_fr:

q = q_ext + q_fr. (2.66)

Equations (2.23) and (2.63) can be then presented as follows:

dq_ext + dq_fr = du +pdv; (2.67)

dq_ext + dq_fr = du + d(pv) + wdw+gdz + dl_mech + dl_fr. (2.68)

As regards Eq. (2.68), inasmuch as

dq_fr = dl_fr,

the quantities dq_fr and dl_fr in this equation cancel out and the equation takes the following form:

dq_ext = du + d (pv) + wdw + gdz + dl_mech (2.68a)

or, which is the same,

dq_ext = dh+ wdw + gdz + dl_mech, (2.68b)

but in Eq. (2.67) dq_fr is not cancelled out, since it is only one of the components of expansion work pdv.

In principle, Eqs. (2.23) and (2.63) are identical. They express analytically the first law of thermodynamics. For this reason the right-hand sides of these equations can be equated. Then,

pdv = du + d(pv) + wdw+gdz + dl_mech + dl_fr (2.69)

Equation (2.69) shows that the work spent to displace the flow, d(pv), to change its kinetic energy, wdw, to change the potential energy of the flow, gdz, to overcome the resistance to flow offered by frictional forces, dl_fr, and the mechanical work, dl_mech, are performed at the expense of the work of expansion done by the gas (or liquid) in the flow, i.e. pdv. For if a flowing gas expands (i.e. if its specific volume increases), work must be accomplished, involved in the increase of v; the differential of this work is always equal to the product pdv.

Inasmuch as

d(pv) = pdv + vdp,

it follows from Eq. (2.69) that for any flow the following is always true:

wdw = - vdp - gdz - dl_mech - dl_fr. (2.70)

For the case where the flow does not perform any mechanical work (dl_mech = 0), we obtain

wdw= - vdp – gdz – dl_fr. (2.71)

When dz = 0, from equation (2.71) it follows that

wdw = - vdp – dl_fr. (2.72)

Finally, for the case of frictionless flow

wdw = - vdp. (2.73)

These important relationships will be used in Chapter 8.