3.1 Cycles. Concept of thermal efficiency. Heat sources

 

In Chapter 2 it was shown that in the process of expansion a gas performs work expended to overcome the forces of external pressure. In accordance with Eq. (2.5a), the work performed by a gas undergoing expansion from pressure p1 to pressure p2 is equal to

 

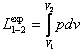                                                                                                                           (3.1)

 

where V1 and V2 are the volumes of the gas at the beginning and end of the process of expansion.

For this process of expansion to be repeated and to obtain the work  again, the gas must be returned into its initial state 1, characterized by the properties p1 and V1 i.e. the gas must be compressed. The gas undergoes then a cyclic process or a cycle.

To compress a gas, naturally, work must be expended and this work is transferred to the gas from some external source. In accordance with the general definition, this work is

 

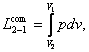                                                                                                                         (3.2)

 

or, which is the same

 

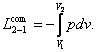                                                                                                                            (3.3)

 

The similarity between the expressions for the work of expansion and compression is illusory: the work depends on the path followed by the process between the same points 1 and 2.

It is then clear that the compression of a gas from pressure p2 to pressure p1 should be carried out, following a path different from the path of expansion. Otherwise, the work of expansion will be equal to the work of compression, and the total work obtained as the gas undergoes a cyclic process (or simply a cycle) will be equal to zero. The work expended by a system per one cycle (we shall refer to it as the work output of a cycle) is equal to the difference (algebraic sum) between the work of expansion and the work of compression. It is clear that the path of compression should be selected so that the absolute value of the compression work is somewhat less than the work of expansion, otherwise the work output of the cycle will be negative, i.e. no work will result from the cycle but only spent, though, as it will be shown below, in certain cases the cycle is organized in exactly this way (refrigeration cycles).

Cycles which result in an output of work are realized in various heat engines. By a heat engine is meant a continuous acting system operating in a cycle and converting heat into work. The substance used to obtain work in a cycle by changing its state is called the working medium (or fluid).

 

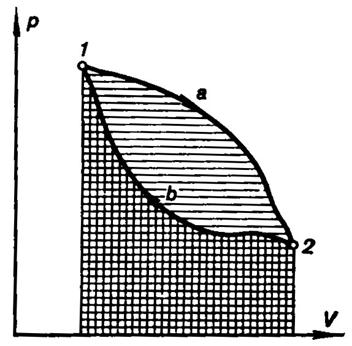
Fig.3.1.jpg

 

Fig. 3.1

 

The work output of a cycle is conveniently interpreted in a p-V diagram, as illustrated in Fig. 3.1. If 1-a-2 is the path of the process of expansion and 2-b-l the path of the process of compression, then the area bounded by the curve 1-a-2 is equivalent to expansion work, and the area below the curve 2-b-1, to the work of compression, while the area confined within the closed curve (path of cycle) 1-a-2-b-1 represents the work output of the cycle. It is clear from this state diagram that for the work output of a cycle to be positive, the path of the process of compression must be located on the p-V diagram below the path of expansion. Let us integrate the differential equation of the first law of thermodynamics

 

                                                                   dQ = dU + dL                                                           (3.4)

 

for an arbitrary cycle realized by a working medium:

 

                                                                                                                     (3.5)

 

It will be recalled that Q is the amount of heat added to the system from the outside (or removed from it), and L denotes work done by the system (or done on the system). Inasmuch as internal energy U is a function of state and, consequently, its integral along a closed path is equal to zero (i.e. as the working medium returns into its initial state upon completion of the cycle, the internal energy of the working medium acquires its initial magni­tude), we obtain

 

                                                                                                                                     (3.6)

 

Denoting

 

                                                                

 

and

 

                                                                    

 

we can present relationship (3.6) in the following form:

 

                                                                        Qc = Lc,                                                                (3.7)

 

i.e. the work output of a cycle, Lc, is equal to the amount of heat added to the working medium from an outside source. In accordance with the first law of thermodynamics, Eq. (3.7) indicates that the work produced by an engine is equal to the amount of heat removed from an external source and added to the working medium of the engine. If it were possible to construct a heat engine in which the amount of work produced would be greater than the amount of heat added to the working medium from an external source, it would mean that the first law of thermodynamics (the law of conservation and conversion of energy) is invalid. From this it would follow that it is possible to construct a heat engine in which work would be accomplished without any addition of heat from the outside i.e. a perpetual motion machine[1]. The first law of thermodynamics, therefore, can be formulated as follows:

A perpetual motion machine of the first kind is impossible.

As regards the heat Qc that is converted into work, it should be noted that in some parts of a cycle heat is added to the working medium and removed from it in other parts. As it will be shown below, the removal of a definite amount of heat from the working medium in some parts of a cycle is obli­gatory for the realization of the cycle of any heat engine.

Denoting the amount of heat added to the working medium in a cycle by Q1 and the amount of heat removed from the working medium in a cycle by Q2, we come to an obvious result:

 

                                                               Qc = Q1 – Q2                                                                                (3.8)

 

and, in accordance with Eq. (3.7),

 

                                                                    Lc = Q1 – Q2.                                                            (3.9)

 

Let us introduce a new concept of the so-called thermal efficiency of a cycle, by which is meant the ratio of the work output of a cycle to the amount of heat added to the working medium during the cycle. Denoting the thermal efficiency of a cycle by ηT, in accordance with the definition given above, we obtain:

 

                                                                                                                             (3.10)

 

or, which is the same,

 

                                                                                                                          (3.11)

 

Accordingly, for 1 kg of the working medium,

 

                                                                                                                               (3.12)

 

or

 

                                                                                                                           (3.13)

 

where l and q represent the work and heat per 1 kg of the working medium.

The thermal efficiency of a cycle characterizes the degree of perfection of the cycle analyzed: the higher the thermal efficiency, the more perfect is the cycle. With an equal amount of heat Q1 added to the working medium, more work Lc is done in the cycle whose thermal efficiency is higher.

When considering processes involving the addition and rejection of heat in a cycle, a question naturally arises: Where does the heat Q1 added in the cycle come from and where is the heat Q2 rejected from the working medium taken to? In this connection let us introduce the concept of heat sources. The system from which the heat Q1, added to the working medium, is removed will be referred to as the high-temperature source, and the system to which the heat Q2, rejected from the working medium, is transferred, as the low-temperature source, or heat sink. For the sake of convenience, it will be assumed below that the total heat capacity of the high- and low-temperature sources is so great that the removal of heat Q1 from the high-temperature source and the transfer of heat Q2 to the low-temperature source does not result in any appreciable change in the temperatures of the two heat sources.

A detailed analysis of the thermodynamic regularities governing the performance of work during the cycles developing in heat engines will be made in the following chapters.

So far, in this section we have been considering cycles on the p-V diagram in which the path of the process of expansion runs higher than the path representing the process of compression, i.e. cycles where work is done and then transferred to an external consumer (Fig. 3.2a). Such cycles are called forward, or direct, cycles. As it was shown above, in a forward cycle an amount of heat Q1 is removed from the high-temperature source and an amount of heat Q2 is added to the low-temperature source, and the difference between these two, Q1 — Q2, is converted into work Lc = Q1 — Q2.

 

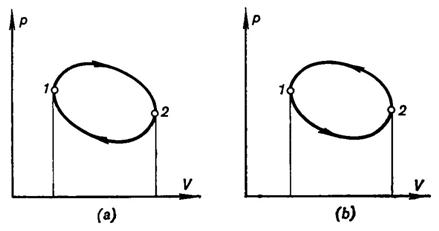
Fig.3.2.jpg

 

Fig. 3.2

 

But if a cycle is realized in a way such that the path of the process of compression is arranged higher than the line representing the process of expansion (Fig. 3.2b), then, inasmuch as the work of compression happens now to be greater than the work of expansion, for such a cycle to be accomplished work must be transferred from some external source of work (the magnitude of this work, of course, is equal to the area between the paths of expansion and compression in the p-V diagram). A reverse cycle results in the removal of heat from the low-temperature source and addition of this heat to the high-temperature source. Denoting, by analogy with the forward cycle, the heat removed from the low-temperature source by Q2 and the heat added to the high-temperature source by Q1 it is clear that Q1 = Q2 + Lc. The heat Q1 transferred to the high-temperature source during the reverse cycle is equal to the sum of the heat removed from the low-temperature source, Q2, and the heat equivalent to the amount of work added during the cycle, Lc. Thus a reverse cycle results in cooling the low-temperature source. The reverse cycle is the working cycle of a refrigerating unit (machine).

 

 

 


[1] A perpetual motion machine of the type considered is called a perpetual motion machine of the first kind, as distinguished from another type of perpetual motion machine, which shall be examined below.