3.10 Reversibility and work
An isolated system is capable of performing work only when it is out of
the state of full equilibrium. If chemical processes are ignored, then for an
isolated system to perform work the pressures or temperatures of the various
component bodies of the system must not be absolutely the same. A system
comprising bodies at different pressures is not in mechanical equilibrium. If a
system comprises bodies at different temperatures, there is no thermal
equilibrium in the system. Only a non-equilibrium system is capable of
producing work. As work is done, an isolated system will approach equilibrium
state.
Consider, for instance, an isolated system consisting of a surrounding
medium whose temperature and pressure remain practically constant and
compressed air with the same temperature as the surroundings but at a higher
pressure. Such a system is in thermal equilibrium, but it is said to be in a
mechanically non-equilibrium state and thus can perform work. For instance, it
can displace a piston in a cylinder until air pressure drops to the pressure of
the surroundings, i.e. until the system comes into the state of mechanical
equilibrium.
If a system comprises two heat sources at different temperatures and a
working body whose initial state is immaterial, we are concerned with a
thermally non-equilibrium system that is capable of performing work, for
instance, when the working body repeatedly undergoes a Carnot cycle. Upon
accomplishing the Carnot cycle not only a certain amount of work is done but
also a certain amount of heat is transferred from the source of heat with a
higher temperature to the source of heat with a lower temperature. But such
heat flow will result in that the temperature of the high-temperature source
decreases and the temperature of the low-temperature source will increase.[1]
In the course of time the temperatures of the two heat sources will become
equal, the system shall reach thermal equilibrium and further performance of
work will become impossible.
Thus, an isolated system can produce work as it passes from a non-equilibrium into an equilibrium state. The amount of
work done depends, as is known, on the nature of the process that the system
undergoes when passing into the equilibrium state.
Consequently, from the point of view of the amount of work done, the
path taken by a system while passing from a non-equilibrium
into an equilibrium state is of great importance.
Let us again assume that we have a thermally non-equilibrium system
consisting of two heat sources at different temperatures and a working medium.
We can visualize a case in which heat is transferred from the high-temperature
source directly to the low-temperature source, by-passing the working medium.
Such a process results in that over a certain period of time the temperatures
of the system component bodies become equal, the system will happen to be in
the state of thermal equilibrium, and no work whatsoever
will be done.[2]
Such mode of heat transfer (evening out of temperatures), proceeding without
work being done, will necessarily occur at a finite temperature difference,
i.e. the process will be irreversible. On the contrary, when the system passes
from a thermally non-equilibrium state into an equilibrium state, maximum work
can be produced as a result of the working medium undergoing repeatedly a
Carnot cycle, in which the highest temperature of the working medium is equal
to that of the high-temperature source, and the minimum temperature of the
working medium is equal to that of the-low-temperature source, i.e. as a result
of the accomplishment of fully reversible processes.
If there is an isolated system not in mechanical equilibrium,
consisting, as before, of compressed air and the surroundings, then the maximum
amount of work can also be obtained while the system passes from the state of
mechanical non-equilibrium into a state of equilibrium, provided fully
reversible processes take place. Suppose that work is done with the aid of a
piston-type air machine. It is clear that under otherwise identical conditions
the work done will be the greater the smaller the friction between the piston
and walls of the machine cylinder is. But friction is a typical irreversible
process. Maximum work would be done if there were no friction at all, i.e. in.
a fully reversible process.
We arrived in this way to the following important conclusions.
(1) An
isolated system is only capable of producing work if it is in a non-equilibrium
state. Upon reaching a state of equilibrium, the availability of the system proves
to be exhausted.
(2) To
obtain the maximum available work when passing from a non-equilibrium state
into a state of equilibrium, all processes which a system undergoes must be
fully reversible.
The problem of determining numerically the maximum useful work,[3]
sometimes referred to as the availability of a system, is therefore of
paramount importance. Imagine having available an isolated system consisting of
surroundings and some body or a totality of bodies, whose pressure p and
temperature T (or one of these properties) differ from the pressure and
temperature of the surroundings. Such a body or a group of bodies shall be
referred to below as a source of work. Let us now define more precisely
the concepts of useful work, maximum work, and the availability of the system concidered. Also assume that the temperature T0 and pressure p0 of the surroundings
remain constant or, if anything, they do not depend on whether heat is added to
or removed from the surroundings. Inasmuch as in the general case p ≠ p0 and T
≠ T0, the
isolated system considered is a non-equilibrium one and is, consequently,
capable of producing work. Let us try to determine the availability of the
system, introducing for this purpose the following notations. Denote by U1 and V1 respectively, the internal
energy and volume of the source of work in the initial non-equilibrium state,
and by U2 and V2 the internal energy and
the volume of the source of work in the final equilibrium (with respect to the
surroundings) state. Denote the initial pressure and temperature of the source
of work by p and T, and
the final (equal to these of the surroundings) pressure and temperature by p0 and T0. Denote the initial
internal energy of the surroundings by U01, and the final by U02. The total internal energy of the system in the
initial non-equilibrium state is
(3.166)
and in the final equilibrium state
(3.167)
Since by definition the system considered is a closed one, work can be
done by the system only at the expense of its internal energy:
(3.168)
or, according to Eqs. (3.166) and (3.167),
(3.169)
But there may be heat exchange between the source of work and the
surroundings; in addition, the source of work may perform work on the
surroundings (against the pressure exerted by the surroundings). Denote the heat
transferred from the source of work to the surroundings by Q0, and the work done by the source of work on the
surroundings by L0. In accordance with the first
law of thermodynamics, expressed by Eq. (2.15a),
(3.170)
Since the pressure of the surroundings is assumed to be constant
(3.171)
and
(3.172)
Substituting the value (U01
– U02) in Eq. (3.169), we obtain:
(3.173)
The heat transferred from the source of heat to the surroundings is evidently
equal to the product of the constant temperature T0 of the surroundings by
the increase in its entropy (S02
– S01), i.e.
(3.174)
Substituting the value of Q0 from Eq. (3.173), we obtain:
(3.175)
Equation (3.175) gives the magnitude of the useful work produced
by an isolated system that passes from a
non-equilibrium state into a state of equilibrium, since subtracted from the
total work produced is a fraction of the work, p0(V2 – V1), which
is spent to compress the surroundings and cannot, therefore, be used at will.
Equation (3.175) does not, however, give the magnitude of the maximum useful
work, or availability, since it fails to imply the condition that all processes
developing in the system must necessarily be reversible.
To find the value of the availability of an isolated system, use should be made of the
assumption that reversible processes do not result in a change in the entropy
of an isolated system. Hence, taking into account the additivity
property of entropy, it follows that if the entropy of the work source
diminishes by S1
– S2, the
entropy of the surroundings must increase by the same value, i.e. for
reversible processes
(3.176)
Accounting for Eqs. (3.175) and
(3.176), we can write the equation for the availability of an isolated system:
(3.177)
As can be seen from Eq. (3.177), the magnitude of the maximum useful
work, or availability, of a system is determined unambiguously by the initial
properties of the source of work and by the properties, or parameters, of the
surroundings.
Consider several concrete examples of determining the maximum useful
work. On the p-V diagram in Fig. 3.20 point 1 represents the
initial state of the source of work[4];
point 2 is determined by the parameters of the surroundings, p0 and T0. As can be seen from
the diagram, points 1 and 2 lie on one isotherm (the isotherm of
the surroundings). Therefore, in its initial non-equilibrium state the isolated
system consisting of a source of heat and the surroundings is in thermal but
not in mechanical equilibrium (p1
> p0). What is then the availability of
the system considered? This simple problem can be solved either by using Eq.
(3.177) or with the aid of the p-v diagram shown in Fig. 3.20. Make use
of the second way, solving the problem by means of the p-v diagram. The
availability of the system will happen to be exhausted after the source of work
passes from the initial state 1 into state 2, i.e. after the
isolated system comes into a state of equilibrium. For the system to produce
the maximum possible work, the process realized by the source of work in
passing from state 1 into state 2 must be fully reversible.
Consequently, it is necessary to determine the possible reversible process (or
the totality of reversible processes) as the source of work passes from state 1
into state 2.
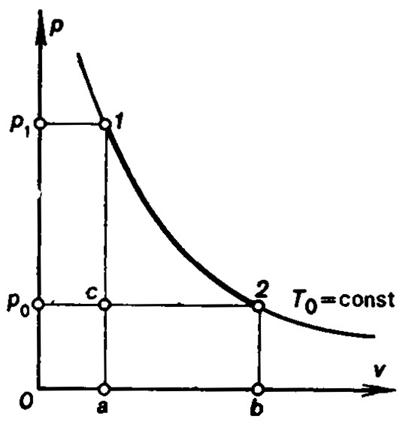
Fig. 3.20
Since the isolated system considered comprises only one source of heat
which is at a constant temperature, namely, the surroundings, the reversible
process can be visualized as proceeding either in the absence of heat exchange
between the source of work and the surroundings (adiabatic expansion or
compression of the source of work) or in the presence of heat flow between the
source of work and the surroundings but at a necessarily constant surroundings
temperature T0
(isothermal expansion of compression of the source of work at a temperature
T0). In all
other processes heat transfer between the source of work and the surroundings
at a finite temperature difference is inevitable. The accomplishment of a
reversible process is then impossible, meaning that the only reversible process
possible between the states 1 and 2 is isothermal expansion of
the gas along the isotherm T0. The work produced by the source of
work in this process is equivalent to the area 1-2-b-a-1 (Fig. 3.20).
But not all the work produced can be utilized at will; a fraction of the
work equivalent to the area a-c-2-b-a is spent inevitably to displace
the surroundings (to overcome the constant pressure p0 exerted by the
surroundings). Consequently, the maximum possible useful work, or the
availability, equal to the difference between the work done and the fraction of
the work spent to ensure the displacement of the surroundings, is equivalent to
the area 1-2-c-1.
The same result can be easily obtained directly from Eq. (3.177). Since
the source of work considered in this example was assumed to possess the
properties of an ideal gas, and inasmuch as the temperature of the source is
the same in the states 1 and 2 and equal to T0, the internal energy of the source of work is also the
same in the states 1 and 2,
and the first member in the right-hand side of Eq. (3.177) is equal to
zero. The second member in this equation represents the amount of heat added to
the source of work in the isothermal process at temperature T0, equal to the work done in this process (internal energy
remains constant). In the course of isothermal expansion, the entropy of the
heat source increases (heat is added), S2> S1, and therefore the second
member in Eq. (3.177) will be positive and numerically equal to the area 1-2-b-a-1
in Fig. 3.20. The last member in the equation will be negative (V2 > V1) and numerically equal to the area a-c-2-b-a. Thus,
= (area 1-2-b-a-1) - (area a-c-2-b-a) = (area 1-2-c-1) is in agreement with the
previously obtained result, as could be expected.
Consider a second example. Assume, as before, that an isolated system
consists of a source of work possessing the properties of an ideal gas and
surroundings. The initial state of the source of work is represented by point 1 on the p-v diagram in Fig.
3.21 (pressure p = p0, temperature T1). As in the preceding example, the process is assumed to
continue until the system comes into the state of equilibrium. Point 2, then, characterizes the
state of the source of work at the temperature and pressure equal to those of
the surroundings, i.e. the state of the source of work in equilibrium with the
surroundings. It is first of all necessary to determine for the source of heat
a possible reverse path from state 1 to state 2. As was already
mentioned, for an isolated system with only one heat source at constant temperature
(surroundings at the temperature T0) the
only reversible processes possible are the adiabatic and isothermal processes
at the temperature T0.
The only possible reverse path which the source of work may follow in
passing from state 1 into state 2 and in which the source is in
equilibrium with the surroundings, is, therefore, the path of adiabatic
expansion from the initial state to the state with the temperature of the
surroundings (adiabatic curve 1-a in Fig. 3.21) and the subsequent
compression at constant temperature T0 (isotherm a-2).
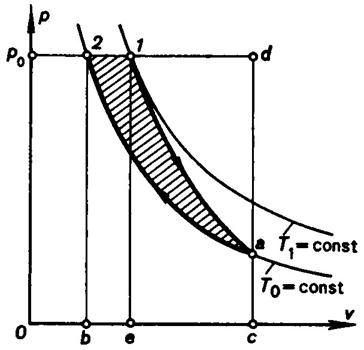
Fig. 3.21
The maximum useful work, just as before, can be determined in two ways:
either from Eq. (3.177) or with the aid of the p-v diagram shown in Fig.
3.21. We first follow the second way. Since in the course of adiabatic
expansion 1-a the pressure of the source of work does not exceed the
pressure of the surroundings p0,[5] the
work done by the gas during this process (equivalent to the area 1-a-c-e-1) is smaller than the work
(equivalent to area 1-d-c-e-1) which
should be expended to compress the surroundings. Hence, not only no useful work
can be produced but for the process 1-a to proceed work equivalent to the
area 1-d-a-1 must be expended. The work required for the accomplishment
of this process can be visualized as being temporarily transferred from an
external source of work. The process of isothermal expansion a-2 demands
an expenditure of work equivalent to the area a-2-b-c-a. This work can
be done by the surroundings whose constant pressure p0 is continuously
greater than the pressure of the source of work.[6]
Furthermore, the work which the surroundings are able to produce, due to a
decrease in the volume of the system, which corresponds to isothermal
compression a-2, exceeds
the work spent to ensure isothermal compression of the source of work by an
amount equivalent to the area d-a-2-d. The unknown maximum useful work
will evidently be equal to the difference between the excess work
(equivalent to the area d-a-2-d)
and the work previously transferred from the external source
(equivalent to the area 1-d-a-1),
i.e.
(area d-a-2-d) - (area 1-d-a-1)
= (area 1-a-2-1).
Just as in the preceding example, the magnitude of can be
determined directly from Eq. (3.177).
The first member in Eq. (3.177), U1 -
U2, represents the work of
adiabatic expansion between the temperatures T1 and T0, irrespective of the initial and final pressures,[7]
and this work will be positive and equivalent to the area 1-a-c-e-1.
The second member in Eq. (3.177) represents the amount of heat
transferred to the surroundings from the source of work. Since during the
process of reversible adiabatic expansion 1-a the entropy of the source
of heat does not change, S1
= Sa,
and, consequently,
(3.178)
The amount of heat added to (or removed from) an ideal gas undergoing an
isothermal process is equal to the work of expansion or compression produced in
this process. The amount of heat removed from the source of heat in the course
of isothermal compression a-2, therefore,
is equal to the work which is equivalent to the area a-2-b-c. Inasmuch
as Sa = S1 < S2 (in the course of process a-2 heat is rejected
from the source of work and, consequently, its entropy decreases), the second
member in Eq. (3.177) will be positive.
Finally, the last member in Eq. (3.177), p0 (V2 – V1), as can be seen from the p-v diagram in Fig.
3.21, will also be positive and numerically equal to
the area 1-2-b-e-l. Thus, the maximum useful work = (area 1-a-c-e-1) + + (area 1-2-b-c-1) - (area a-2-b-c-a) = (area 1-a-2-1).
In the example considered, the system can be seen to produce work,
resulting in that the volume occupied by the source of work decreases and the
volume occupied by the surroundings increases, accordingly.
In Figs. 3.22 and 3.23 the shaded areas represent as before the
magnitudes of the maximum useful work for the next two examples. In the first
case (Fig. 3.22), in the initial state the system is out both of thermal and
mechanical equilibrium since the temperature and pressure of the source of work
is greater than T0
and p0. In the second case (Fig.
3.23), the system is also out of thermal and mechanical equilibrium in the
initial state, but here T1
< T0
and p1
< p0. The maximum useful work is determined
in both cases in a similar manner.
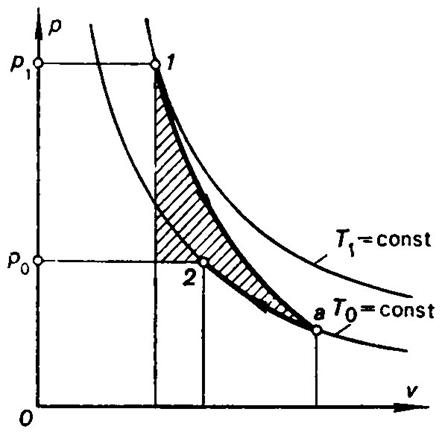
Fig. 3.22
The concept of the maximum useful work of heat, or the availability
due to heat, is of a more practical importance than the concept of the
maximum useful work (the availability) of an isolated system.
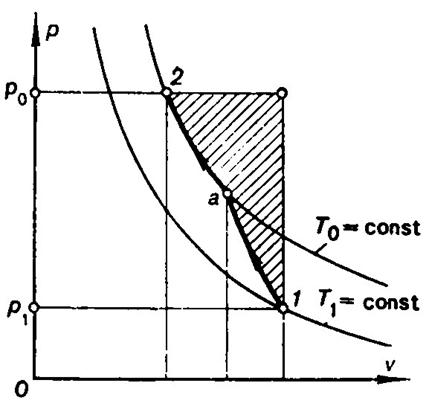
Fig. 3.23
Speaking of availability due to heat, we must consider an isolated
system as consisting of two heat sources (a high-temperature source and a
low-temperature source) and of the working medium undergoing a cycle. The
surroundings, which are at a constant temperature T0 and pressure p0, are considered, as above,
to be the low-temperature source, and usually (but not always) we consider the
high-temperature source to be an infinitely large source which, consequently,
is at a constant temperature T1.
The availability due to the heat removed from the high-temperature
source at a temperature T1
is denned as the maximum useful work which can be obtained at the expense
of this heat, provided the surroundings (at temperature T0) are the low-temperature source. The availability due to
heat will be denoted by 
.
It will be recalled that the greater the difference between the temperature of the high- and low-temperature sources, the
larger is the fraction of the heat which can be removed from the
high-temperature source and converted into work in the cycle.
It should be clearly understood that since the working medium undergoes
a cyclic process, its internal energy does not change upon completion of the
cycle and, therefore, work can only be done at the expense of the heat Q1 added to the working medium from the high-temperature heat
source. It is essential to note that the availability due to heat does not
depend on the pressure of the surroundings p0, since
the volume of the working medium does not change as a result of the cyclic
process, the surroundings do not undergo compression or expansion, and the
entire work done by the working medium can be utilized at our discretion, i.e.
it is useful work. The fraction of the heat Q1 that is converted into
work in the cycle is the greater, the higher the efficiency of the cycle
involved.
As was shown above, in a given temperature interval the maximum
efficiency is offered by a reversible Carnot cycle. Thus, the maximum useful
work produced by a certain amount of heat Q1 rejected
from a high-temperature source at a temperature T1 can be obtained when
the system considered undergoes a reversible Carnot cycle.
It follows from the above conclusion that
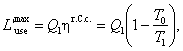(3.179)
where ηr.C.c.
is the thermal efficiency of the reversible Carnot
cycle operated between temperatures T0 and T1.
As can be seen from Eq. (3.179), the availability due to heat is the
greater the smaller the ratio T0/ T1. If the
temperatures of the heat source and heat sink are the same (T0 = T1), the availability
due to heat is equal to zero.
If an irreversible cycle is operated between the two heat sources, the
useful work produced by the heat rejected from the high-temperature heat source
will be smaller, than the availability due to heat, since the thermal
efficiency of any irreversible cycle is always smaller than the thermal
efficiency of a reversible Carnot cycle.
As we already mentioned, the useful work done by an isolated system (or
by the heat removed from a high-temperature heat source) is the maximum
possible work, provided that reversible processes proceed in the system. It
will be once more noted that any irreversibility causes a decrease in the
amount of useful work which can be done by the system. It is obvious that the
useful work done by a system (or the useful work done by heat) will be the
smaller, the greater the irreversibility of the processes, with the measure of irreversibility
being expressed by the increase in the entropy of the isolated system
considered. That is why the decrease in the amount of useful work (often
referred to as the loss of availability) and the increase in the entropy of a
system due to irreversibility must be related unambiguously. The nature of this
relationship can be easily established.
The amount of useful work done by an isolated system where irreversible
processes take place, the system consisting of a source of work and
surroundings, was shown to be determined from Eq. (3.175):
and the amount of the maximum useful work done by this
system is determined from Eq. (3.177)
where S01
and S02
are the initial and final entropies of the surroundings, and S1 and S2 are the initial and
final entropies of the source of work.
It is clear that reversible process proceeding in an isolated system is
since the entropy of the isolated system does not change in
this case.
But since Eq. (3.175) was derived for useful work, Luse, i.e. for the
case when a system undergoes irreversible processes, and Eq. (3.177) was
derived for the maximum useful work, , i.e.
for the case when only reversible processes proceed in a system, we have
and thus
(3.180)
where ΔSsys = [(S02
- S01) - (S1 - S2)] is the increase in the system's entropy as the
result of the irreversible process proceeding in it.
It should be emphasized that is the
maximum possible work which a given isolated system is able to produce,
provided that the processes leading this system to a state of equilibrium are
reversible; Luse
is the amount of work done by the same system if the processes proceeding in it
are irreversible. The difference between these two amounts of work is defined
as the loss of availability of the system due to the irreversibility of the
process proceeding in it. From Eq. (3.180) it follows that the greater the
measure of irreversibility of these processes, i.e. the greater the quantity ΔLsys,
the greater the loss of availability of the system.
Equation (3.180) is of universal importance. In
particular, for an isolated system comprising a heat source, a heat sink, and a
working medium undergoing a cycle.
In fact, the amount of work done by a certain amount of heat Q1 rejected from the
high-temperature source can be presented as the difference between Q1 and the amount of heat
Q2 added
to the low-temperature sink during the cycle:
(3.181)
Since, as it was assumed above, the temperature of the low-temperature
source (the surroundings) remains constant, Q2 can be expressed as
(3.182)
whence
(3.183)
Since the working medium undergoes a cycle, all its properties do not
change no matter whether the processes proceeding in the system are reversible
or irreversible. The entropy of the high-temperature source decreases, since
heat is removed from this source, and the entropy of the low-temperature source
increases. Since the total entropy of the system does not change when the
processes developing in it are reversible, the increase in the entropy of the
low-temperature source ΔSl.t. must be equal to the decrease in
the entropy of the high-temperature heat source ΔSh.t..
Inasmuch as the irreversibility of all processes proceeding in the
isolated system considered corresponds to the case when the maximum useful work
produced by heat is obtained, with account taken of ΔSh.t. = ΔSl.t.
Eq. (3.183) gives:
(3.184)
[it can be easily shown that this equation is identical with
the previously derived equation (3.179) for the availability due to heat;
indeed, since in accordance with Eq. (3.135) the absolute value of
(3.185)
substituting this quantity in (3.184) we get Eq.
(3.179)]. From Eq. (3.183) and (3.184) it follows that
(3.186)
Since, as was already mentioned above, the entropy of the working medium
undergoing a cycle does not change, it is clear that the difference between ΔSl.t.
and ΔSh.t.
represents the change in the entropy of the entire isolated system considered:
Taking the above relationship into account, we obtain from Eq. (3.181)
the formula for the loss of availability of heat due to the irreversibility of
the processes proceeding in the isolated system considered:
(3.187)
This relationship is identical with Eq. (3.180).
Denoting the loss of availability by ΔL, Eqs. (3.180) and
(3.187) take the following form
(3.188)
The loss of availability ΔL is sometimes referred to as the energy
loss. Equation (3.188) is called the Gouy-Stodola
equation after the French physicist G. Gouy, who was
the first to derive this equation in 1889, and the Slovak scientist and
engineer. A. Stodola, who was the first to use this
equation to solve engineering problems. Gouy-Stodola's
equation finds wide application in analyzing the effectiveness of heat plants.
The determination of ΔSsys is an intricate problem and it must be
solved for each real process individually; examples for the calculating ΔSsys
are given in Sec. 9.4, Ch. 9.