3.2 Reversible and irreversible processes
One of the most important notions of thermodynamics is the notion of reversible
and irreversible processes.
A thermodynamic process is defined as a totality of continuously
changing states of a thermodynamic system. Two processes can be imagined to
develop along the same path between any two states 1 and 2 of a
system: from state 1 to state 2 and vice versa, from state 2 to
state 1, the so-called
forward and reverse processes.
A process is said to be reversible if after the process has been
completed in the forward and reverse directions, the system returns into its
initial state. Thus, the totality of the forward and reverse processes causes no
changes in the surrounding medium.
Let us consider, for instance, two planes A and
B with a ball placed at point 1 on one of the planes (Fig. 3.3).
As the ball moves downward, it acquires kinetic energy at the expense of
potential energy. At point 3 the ball possesses a certain amount of
kinetic energy, making it possible for the ball to rise to the other plane; its
kinetic energy diminishes, but this is compensated for by an increase in the
potential energy. If there is no friction between the ball and the surface over
which it moves and the surrounding air offers no resistance to the motion of
the ball, in accordance with laws of mechanics the ball shall rise to the same
height from which its downward movement on plane A was initiated, i.e. points
1 and 2 are arranged at the
same height h above the horizon. The ball will cease to rise at point 2,
its velocity will become equal to zero and the ball will begin to roll
down, then rise to point 1, etc.
Under the conditions specified above (absence of surface friction and
resistance of air to motion) the considered process is reversible.
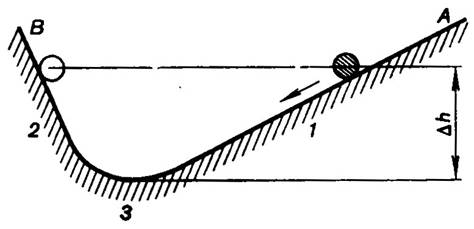
Fig. 3.3
For reversible processes, the reverse process is, so to say, a
"mirror-image presentation" of the direct process. If, for instance,
in a forward process a certain amount of heat is added to a system, in the
reverse process an exactly-equal amount of heat is rejected from the system; if
a system performs work in a forward process on the surrounding medium, then
during the reverse process the surrounding medium does work on the system, the
absolute amount of this work being equal to the work done during the forward
process. If a system undergoes expansion during a forward process, compression
of the system will take place during the reverse process, etc.
A process is said to be irreversible if after the process has
been completed in the forward and reverse orders, the system fails to return
into the initial state. It is a matter of general experience that all natural
spontaneous processes are irreversible, and no natural reversible processes
exist.
Let us consider some examples of irreversible processes.
A typical example of an irreversible process, accompanying many natural
processes, is the above-mentioned process of friction. The work expended to
overcome friction turns irreversibly into the heat, which is liberated in the
course of friction.
The presence of friction always results in the absolute value of the
work output of a system undergoing a direct process being smaller than the work
transferred into the system from the outside during the reverse process. This,
for instance, explains the fact that in reality the ball, moving from one
inclined plane to the other and back, rises each time to a smaller height,
until it comes to a standstill at the bottommost point. To overcome friction
and the resistance offered by the surrounding medium an irreversible
expenditure of energy takes place, and the process develops spontaneously in
one direction, until the system comes into the state of rest.
The process occurring in a wound up clock also develops in one
direction, the spring unwinds (or the weight falls) and the pointers move.
Naturally, the clock will not wind up by itself, without the transfer of work
from the outside.
The expansion of a gas into an evacuated space, considered, above in
Sec. 2.4 (the Gay-Lussac—Joule experiment), is also a typically irreversible
process. It is clear that the gas, occupying volume V1 before expansion and filling the volume V2 after expansion, will not be compressed without the expenditure
of work from the outside, and will not accumulate again in volume V1 freeing volume V2.
The thing that makes any mechanical processes irreversible is friction.
As was already mentioned, in the absence of friction any mechanical process is
reversible. For this process to be accomplished in the reverse order, it is sufficient
to change the signs of the velocities of all the components of the system.
The process involved in making any solution or mixture is also
irreversible. If alcohol is mixed with water, for instance, the components of
the resulting solution will not separate by themselves.
The flow of electric current in a conductor is accompanied by
irreversible losses, which are Joule's losses of power to overcome the
resistance of the conductor; these losses result in that electric power turns
into heat. The magnitude of these losses, similar to the losses in mechanical
processes due to friction, is independent of the direction in which the current
flows in a conductor.
The irreversible process which is often encountered in practice consists
in the flow of heat from a body with a higher temperature to a body with a
lower temperature. The century-old experience of mankind shows that heat will
not flow spontaneously from a body at a higher temperature to a body at a lower
temperature without the expenditure of external work.
It should be noted that the degree of irreversibility of this or another
process can be different. For instance, work shall be expended to overcome the
frictional forces both when a polished body moves over a polished surface and
when a body moves over a rough surface, but the magnitude of the work converted
into frictional heat is greater in the second case than in the first. Below, in
this chapter, an objective criterion will be introduced, enabling a qualitative
estimation of the degree of irreversibility of various real processes.
Each of the irreversible processes considered above can be realized in
the reverse direction, returning the system into its initial state. But for such
a reversible process to be accomplished, the surroundings must undergo a
compensating process (involving the expenditure of heat or work).
So, in the example with the ball rolling from an
inclined surface, the ball can also be lifted to point 2 in the presence
of friction, but to make this possible it is necessary to spend work equal to
the decrease in the energy of the ball, due to friction. This work must be
transferred from some external source. The gas expanding in the Gay-Lussac —
Joule experiment can again be returned into vessel 1 if, for instance, a
vacuum pump is employed for the purpose. However, work will be expended to
drive this pump. The components of the aqueous alcohol solution considered
above can be separated by means of rectification, but this involves the
expenditure of a certain amount of heat. And, finally, heat can be transferred
from a body at a lower temperature to a body at a higher temperature (this is
carried out with the aid of the above-mentioned reverse cycle of the heat engine
used in refrigerating plants), but this process is feasible provided a certain
amount of work is expended.
It should be noted, however, that an irreversible process cannot be
reversed completely. A system is returned into its initial state at the expense
of irreversible changes in the surroundings.
It must be stressed that any spontaneous (and, consequently,
irreversible) process occurring in a system goes on until equilibrium sets in
the system.
Practice shows that after a system reaches equilibrium it remains in
this state, i.e. the system is incapable of a spontaneous change in state,
which complies with the previously formulated statement that energy spontaneous
process is irreversible[1].
It is important to visualize
clearly that a system can be brought into a state of equilibrium by having the
system to undergo both reversible and irreversible processes.
Based on the foregoing, it is easy to come to the conclusion that a system is capable of producing
work until it passes into a state of equilibrium. In fact, it was noted above that any
heat engine can perform work, provided there are at least two heat sources
available, a high-temperature source and a low-temperature source (heat sink). If
the temperatures of the high temperature source and sink become equal, i.e. if
the system comprising the high-temperature source, the working medium or
substance and the low-temperature source (heat sink) comes into thermal
equilibrium, the transfer of heat terminates and no work will be done.
The examples considered above show that the absence of equilibrium in a
system is evidenced by the presence in this system of a difference between some
characteristic quantities; this may be either a temperature-difference in
various parts of the system, or a difference in electrical potentials, etc.
As was already mentioned above, the degree of irreversibility of an irreversible
process may differ. In principle, the degree of irreversibility may be
visualized as being so small that the process could be practically realized in
a reversible way. In this connection it is helpful to turn to the concept of
equilibrium (quasi-static) and non-equilibrium processes.
Any non-equilibrium process becomes an equilibrium one, if the rate at
which the process is realized approaches zero. At the same time every
non-equilibrium process is irreversible and every equilibrium process is a
reversible one. In other words, the reason for the irreversibility of real
processes consists in their being in a non-equilibrium state. Indeed, an
infinitely slow (quasi-static) development of a process makes the process
reversible. In an infinitely slow process the working medium passes through a
continuous series of equilibrium states, which may be reproduced while the
system undergoes the reverse process. Irreversible processes, which are the
result of the finite rate at which they are realized, pass through the
non-equilibrium states of the working medium, which states cannot be reproduced
when the process is reversed. For instance, with a finite piston velocity, the
layers of gas adjacent to the piston during expansion are at a pressure lower
than the average pressure of the gas involved and during compression at a
higher pressure. This process is internally irreversible. The internal
reversibility-results from the constancy of the parameters (properties) over
the entire mass of the working medium, as distinguished from the external
irreversibility which stems from the infinitely small difference between the
temperature of the working medium and of the heat source, which makes possible
a change in the direction of the heat flux during the reverse development of
the process. As was already mentioned repeatedly, heat flows from one body to
another only when the two bodies are at different temperatures. Thus, the
process of heat transfer is, essentially, a non-equilibrium irreversible
process. But if the difference between the temperatures of the bodies is
infinitely small, the degree of irreversibility is also infinitely small, i.e.
the irreversible process of heat transfer happens to be as close as possible to
a reversible process. It should be noted that if the difference between the
temperatures of two bodies is infinitely small, the rate of heat transfer
between them will also be infinitely small.
In spite of the fact that it is practically impossible to realize
reversible processes, the concept of a reversible process proves to be very
useful. The point is that, firstly, real processes may be close to reversible
ones in some cases and, secondly, it is more convenient to consider the degree
of irreversibility of a real process in respect to the hypothetically
reversible process.