3.6 Entropy

 

Let us turn now to consider some essential properties of reversible cycles. The thermal efficiency of a reversible Carnot cycle is found from the relationship

 

                                                             

 

In the most general form, by definition, the thermal efficiency of any cycle

 

                                                            

 

from which it follows that for a reversible Carnot cycle

 

                                                                                                                   (3.107)

 

or, which is the same,

 

                                                                                                                                  (3.108)

 

In the general form Eq. (3.108) becomes[1]

 

                                                                                                                      (3.109)

 

Equation (3.109) can be presented in the form

 

                                                                                                                           (3.110)

 

Consider an arbitrary reversible cycle. It will be recalled that to accomplish an arbitrary reversible cycle an infinite number of heat sources must be available. It will also be recalled that, as it was made clear in Sec. 3.4, any reversible cycle can be visualized as consisting of a multitude of elementary Carnot cycles (Fig. 3.8), each of which is associated with a high-tempe­rature source from which it receives heat ΔQ1 and with a low-temperature source to which it transfers heat ΔQ2.With account taken of Eq. (3.109), we can write for each of these elementary cycles (denote their total number by n):

 

1st cycle                                            

 

2nd cycle                                           

 

                                                          .…………………..

 

nth cycle                                           

 

Adding these relations, we obtain:

 

                                                                                                         (3.111)

 

or, by analogy with Eq. (3.110),

 

                                                                                                                              (3.112)

 

In the limit, if infinitely small cycles are considered,

 

                                                                                                             (3.113)

 

whence, is accordance with Eq. (3.112), we obtain:

 

                                                                                                                                (3.114)

 

The integral in Eq. (3.114) is called the Clausius integral. Equation (3.114) shows that for any reversible cycle the Clausius integral is equal to zero. Let us elucidate the properties of the integrand. Denote it by

 

                                                                                                                           (3.115)

 

Upon substitution, Eq. (3.114) reduces to

 

                                                                                                                             (3.116)

 

It can be readily shown that the magnitude of the integral along any closed path, between two arbitrary states A and B as limits (Fig. 3.12) does not depend on the path of the process, but depends on the final states, i.e.

 

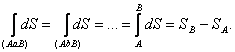                                                                                 (3.117)

 

Thus, the integrand S, similar to interval energy and enthalpy, is a function of state, and its magnitude is determined unambiguously by the properties (parameters) of state. It will also be recalled that as it was mentioned in Sec. 2.4, the differential of a function of state is a total differential.

 

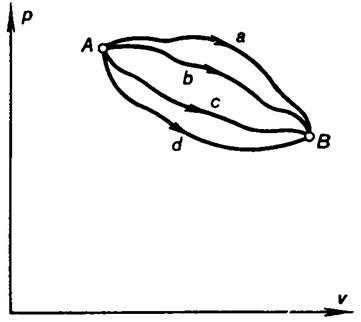
Fig.3.12.jpg

 

Fig. 3.12

 

Heat (just as work) is a function of the process, and the amount of heat added to, or removed from, a system depends on the path of the process. Similar to any function of the process, the differential of the amount of heat, dQ, is not a total differential[2]. On the other hand, it follows from the foregoing that being multiplied by the quantity 1/T, this differential dQ turns into a total differential dS = dQ/T. Thus, the quantity 1/T is an integrating factor for the differential of the amount of heat (it will be recalled that in mathematics by an integrating factor is meant a function µ such that after multiplication by this factor the quantity dX, which is not a total differential, turns into a total differential dY = µdX; it is known from mathematics that in the event of two variables, it is possible to find an integrating factor for any expression that is not a total differential.

The function S introduced by Clausius is called the entropy.

Entropy is an extensive property and, similar to other extensive quantities, it possesses the property of additivity. The quantity

 

                                                                                                                               (3.118)

 

is referred to as specific entropy, and is defined as the entropy of a unit mass of substance.

Just like any other function of state, the specific entropy of a system can be presented as a function of any two properties of state, x and y:

 

                                                                                                                         (3.119)

 

where p and v, p and T, etc., can be present as x and y.

The methods used to calculate the entropy of a substance with the aid of other thermal quantities will be treated in detail in Chapters 4 and 6.

The definition of entropy (3.115) makes it clear that entropy is measured in units of heat divided by temperature. The most commonly used units of entropy are J/K.

The units of specific entropy are J/(kg·K), kJ/(kg·K), sometimes kcal/(kg·K) and etc. Thus, the unit of measurement of entropy coincides with that of heat capacity. For a pure substance and for a mixture of substances not reacting chemically with each other the zero for entropy can be chosen arbitrarily, just as the zero for internal energy. In considering various thermodynamic processes, we will be interested in the change of the entropy involved in these processes, i.e. the difference between the entropies at the initial and final points of the processes, which, naturally, depends in no way on the entropy zero point.

It is clear from definition (3.115) that in various reversible processes the entropy of a system can either increase or diminish: inasmuch as temperature T is always positive, from equation (3.115) it follows that when heat is added to the system (dQ > 0), its entropy increases (dS > 0), and when heat is removed from the system (dQ < 0), its entropy decreases (dS < 0). It follows from Eq. (3.115) that when in a reversible process a body undergoes a change from the initial state 1 to the final state 2, the entropy of the body changes by

 

                                                                                                                   (3.120)

Calculate, for example, the change in the entropy of 10 kg of water heated from a temperature of T1 = 20 °C to a temperature T2 = 60 °C at atmospheric pressure; in this temperature interval the heat capacity of water is assumed at first approximation to be independent of temperature and equal to 4.19 kJ/(kg·K). Since

 

                                                             

 

we take G and cp out of the integral, and from Eq. (3.120) we get:

 

                                                        

 

or

 

                                  

 

One important fact should be specially emphasized. The concept of entropy was introduced by investigating reversible cycles. This would seem to make it impossible to investigate the concept of entropy in the analysis of irreversible processes. But it must be borne in mind that entropy is a function of state and, consequently, the change of entropy in any process is only defined by the final and initial states.

The concept of entropy permits the introduction of the temperature-entropy chart, or diagram, in which entropy is plotted along the abscissa, and absolute temperature along the ordinate (Fig. 3.13). This chart facilitates to a great extent the analysis of heat engines. Let us plot the curve (path) of an arbitrary process on the T-S diagram.

 

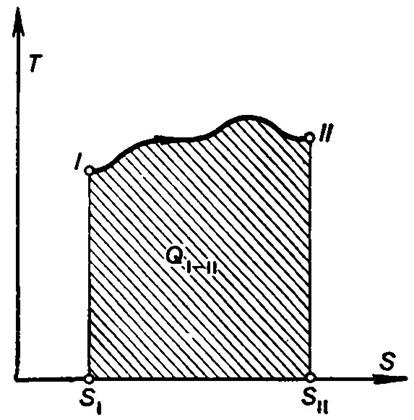
Fig.3.13.jpg

 

 

Fig. 3.13

 

From Eq. (3.115) it follows that in a reversible process

 

                                                                                                                           (3.121)

 

The amount of heat added to a system (or removed from it) in a reversible process between the states I and II is:

 

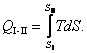                                                                                                                       (3.122)

 

It is clear that the amount of heat received (rejected) by a system in a reversible process will be represented on the T-S diagram by the area under the path of the process. Fig. 3.14 shows a reversible cycle of a heat engine on a T-S diagram. The amount of heat Q1 added to the working medium in the cycle is represented by the area under the curve ABC, and the amount of heat Q2 removed from the working medium is represented by the area under the curve CDA. The work done by the working medium in the cycle, Lc = Q1 - Q2, is represented on the diagram by the area confined by the closed curve ABCDA.

 

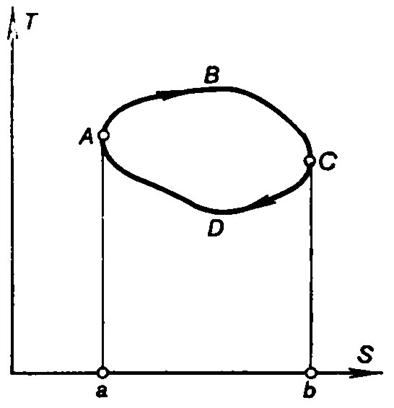
Fig.3.14.jpg

 

 

Fig. 3.14

 

The T-S diagram is convenient since it gives a visual presentation of the amount of heat added and removed (rejected) in a cycle and the work obtained due to the accomplished cycle (or the work expended if a reverse cycle is involved). The T-S diagram also shows where in the process heat is added to the working body and where heat is removed from it: the process of reversible addition of heat is characterized by an increase in entropy, and the process of heat removal by a decrease.

An isothermal process is evidently represented on the T-S diagram by a horizontal straight line.

It follows from Eq. (3.122) that in the isothermal process

 

                                                          

 

It is clear from equation

 

                                                                 

 

that in a reversible adiabatic process (dQ = 0)

 

                                                                                                                               (3.123)

 

or

 

                                                                                                                           (3.124)

 

That is why reversible adiabatic processes are also referred to as isentropic, and the path of such a process is called an isentropic, which in the T-S diagram is represented by a vertical line.

It ought to be noted that in the T-S diagram, just as in any other thermodynamic diagram of state, only reversible equilibrium processes can be plotted.

A reversible Carnot cycle is represented on the T-S diagram by the rectangle 1-2-3-4-1 (Fig. 3.15), bounded by isotherms 1-2 (T1 = const) and 3-4 (T2 = const) and by reversible adiabats 2-3 (S2 = const) and 4-1 (S1 = const).

 

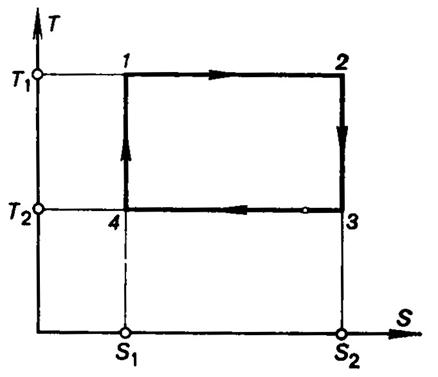
Fig.3.15.jpg

 

 

Fig. 3.15

 

The amount of heat added in this cycle to the working medium from the high-temperature heat source,

 

                                                                                                                 (3.125)

 

is represented on the diagram by rectangle 1-2-S2-S1-1; the amount of heat transferred to the low-temperature source,

 

                                                                                                                      (3.126)

 

by the rectangle 3-S2-S1-4-3; and the work output of the cycle,

 

                                                                  

 

is represented by rectangle 1-2-3-4-1.

From the general expression for the thermal efficiency of a cycle, and with account taken of Eqs. (3.125) and (3.126), for a reversible Carnot cycle we obtain:

 

                                                            

 

or, which is the same,

 

                                              

 

which coincides with Eq. (3.32), as was to be expected.

The T-S diagram has made it possible to prove easily the validity of the following statement:

The thermal efficiency of any reversible cycle realized between more than two heat sources is less than the efficiency of a reversible Carnot cycle realized between the same limiting temperatures.

Compare the arbitrary reversible cycle I with the Carnot cycle II that operates in the same temperature interval of cycle I (Fig. 3.16). Plot the Carnot cycle 1-2-3-4 around cycle I, and give the Carnot cycle the name III. Then

 

                                                 (3.127)

 

                                                                                     (3.128)

 

whence it follows that

 

                                                                                                                                  (3.129)

 

Thus, within a given temperature interval the thermal efficiency of a reversible Carnot cycle is greater than the thermal efficiency of any other reversible cycle. The reversible Carnot cycle is, consequently, a kind of a standard, enabling to determine the effectiveness of any other cycle operated in the same temperature interval, by comparing the thermal efficiency of this cycle with that of the Carnot cycle. This is the special importance of Carnot cycle, distinguishing it among any other cycles of heat engines.

 

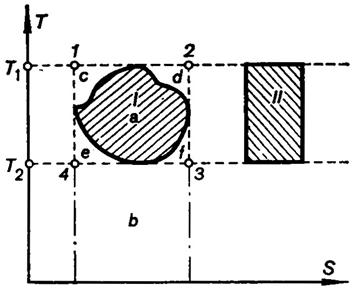
Fig.3.16.jpg

 

 

Fig. 3.16

 

The greater any arbitrary cycle fills the rectangle representing the reversible Carnot cycle, operated in the same temperature interval and in the same interval of entropies (as it is said, the higher the cycle-filling coefficient or the area ratio of a cycle), the higher the thermal efficiency of this arbitrary reversible cycle is. The cycle of any heat engine should be organized so that the area ratio of this cycle is as large as possible.

Let us turn now to the analysis of one more important variety of cycles of heat engines. Consider the reversible cycle, represented on the T-S diagram in Fig. 3.17 and consisting of two isotherms and two arbitrary equidistant curves.

 

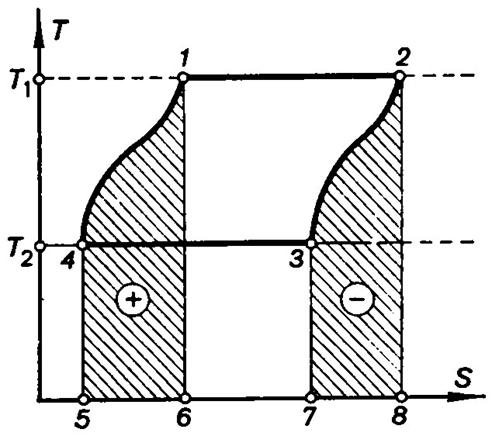
Fig.3.17.jpg

 

 

Fig. 3.17

 

The curves 4-1 and 2-3 are equidistant, and to accomplish the reversible processes corresponding to these curves there should be available an infinitely large number of heat sources.

During the process 2-3 heat is removed from the working medium (-) in an amount determined by the area 2-8-7-3-2 and equal to the heat added to the working medium during the process 4-1 and determined by the equal area 1-6-5-4-1. The heat sources can be replaced by so-called regenerators, which during the process 6-1 reject the amount of heat (and at the same temperatures) returning to them from the working medium during the process 2-3. The cycle results in that each of the infinitely large number of heat regenerators neither rejects nor receives heat on the whole. The heat added to the working medium in the cycle, Q1 = T1 (S2 – S1), is represented by the area 1-2-8-6-1, and the heat rejected in the cycle, Q2 = T2 (S3 - S4), by the area 3-7-6-5-4-3. In consequence of the curves 4-1 and 3-2 being equidistant,

 

                                                           

 

whence

 

                                                        

 

The cycle considered above is known as the cycle with complete regeneration of heat, or the regenerative cycle. The regenerator effectiveness, determined by the ratio of the area (+) to the area (-), is equal to unity in this cycle, with a regenerator effectiveness less than unity the cycle is said to be a cycle with incomplete regeneration. An increase in the regenerator effectiveness brings this cycle closer to the Carnot cycle, and in the limit, as it can be seen from the case considered,

Thus, the thermal efficiency of any reversible cycle, accomplished between two heat sources (i.e. a regenerative cycle), is equal to the thermal efficiency of the reversible Carnot cycle operated in the same temperature interval.

Incomplete heat regeneration also increases the thermal efficiency of any (both reversible and irreversible) cycles, since regeneration always increase the area ratio of a cycle.

 

 

 


[1] It should be noted that the sign for Q is chosen arbitrarily. For instance, in a forward cycle performing work, in relation to the working medium Q2 should have a minus sign (since heat is removed from the working medium), and in relation to the low-temperature source a plus sign is proper (since Q2 is added to the heat source).

[2] This is treated at greater length in Sec. 4.1.