3.7 Change of entropy in irreversible processes

 

So far we have been considering the change of entropy only in reversible-processes. Let us turn now to the problem associated with the change of entropy in irreversible processes and, in particular, in irreversible processes proceeding in an isolated system, which are of the greatest interest. Isolated is the name given to a system with a rigid boundary with ideal heat insulation. The ideal heat insulation prevents any heat exchange between the system and the surroundings (dQsys = 0), and the rigid boundary protects the system against any exchange of expansion work with the surroundings. Sine dQsys = 0 and p dVsys = 0, it is clear from Eq. (2.37a) that dUsys = 0, i.e. Usys = const. The analysis of the processes proceeding in an isolated system is of interest mostly because in the limit any non-isolated system and its surroundings can be treated as an integral isolated system.

Inasmuch as for an isolated system dQsys = 0, any process proceeding in such a system is an adiabatic process for the system as a whole.

Consider an isolated system comprising two bodies at different temperatures T1 and T2 with T1 > T2. Heat transfer will take place between these bodies of the system; heat will flow from the body at the higher temperature T1 to the body at the lower temperature T2. If an amount of heat dQ flows from the first body to the second, consequently, in accordance with Eq. (3.115), the entropy of the first body will be reduced by

 

                                                                                                                       (3.130)

 

and the entropy of the second body will increase by

 

                                                                                                                               (3.131)

 

It is clear that the total change in the entropy of the entire system is

 

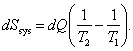                                                                                                           (3.132)

 

Since

 

                                                                       

 

we have

 

                                                                                                                                 (3.133)

 

i.e. an irreversible process results in an increase in the entropy of an isolated system.

If the process of heat transfer between the component parts of the system was reversible (it will be recalled that the condition for the reversibility of a process is an infinitesimal temperature difference T1 - T2 = dT), the entropy of the first body would diminish by

 

                                                              

 

and the entropy of the second body would increase by

 

                                                                 

 

so that for the system as a whole the change in entropy would he negligibly small:

 

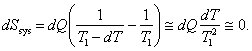                                                                                  (3.134)

 

Another method of reversible heat transfer from a body at a higher temperature to a body at a lower temperature involves, as already mentioned, the Carnot cycle. To realize any irreversible cycle, a system consisting of three elements out of equilibrium - a high-temperature heat source, a low-temperature heat sink, and a working medium - must be available. If during one cycle heat Q1 is removed from the high-temperature heat source (at temperature T1) and heat Q2 is added to the low-temperature heat sink (at temperature T2), the entropy of the high-temperature heat source will diminish by

 

                                                                                                                       (3.135)

 

and the entropy of the low-temperature sink will increase by

 

                                                                                                                         (3.136)

 

As regards the entropy of the working medium, since upon completion of the cycle the working medium returns into its initial state, its entropy does not change:

 

                                                                                                                               (3.137)

 

Hence, after a system undergoes a cycle the change in the entropy of the system considered is equal to

 

                                                                             (3.138)

 

Equation (3.138) is true for any reversible and irreversible cycles operated between two heat sources (a source and a sink).

As was shown above, for a reversible Carnot cycle,

 

                                                                                   

 

Hence, if a reversible Carnot cycle is realized in a system (or any other cycle is accomplished between a heat source and a heat sink), the entropy of the system does not change:

 

                                                                                                                             (3.139)

 

The same conclusion can be drawn for reversible cycles realized between any number of heat sources.

But if a system undergoes an arbitrary irreversible cycle, the entropy of the system will change without fail. The thermal efficiency of any irreversible cycle,  has. been shown above to be less than the thermal efficiency of a reversible Carnot cycle,  realized between the same heat sources.

Bearing in mind that for a reversible Carnot cycle

 

                                                            

 

and, in accordance with the general definition for irreversible cycle:

 

                                                           

 

the inequality

 

                                                                                          

 

can be presented in the following form:

 

                                                                                                                                                         (3.140)

 

whence it follows that for an irreversible cycle

 

                                                                                                                                  (3.141)

 

(here the temperatures refer not to the working medium but to the heat sources). Hence, if an irreversible process is accomplished between two heat sources, the entropy of the system increases:

 

                                                                                                                                 (3.142)

 

The same conclusion is true for irreversible cycles realized between any other number of heat sources.

The increase in the system's entropy is associated with the fact that the entropy of the working medium does not change during the cycle, and the drop in the entropy of the high-temperature sources is less than the increase in the entropy of the low-temperature sources. Thus, an irreversible cycle results in an increase in the entropy of an isolated system.

This conclusion can be proved in the most general form in the following manner. The inequality (3.141), which is true for an irreversible Carnot cycle, as well as for any irreversible cycle, can be presented in the following form:

 

                                                              

 

or, which is the same,

 

                                                                                                                                (3.143)

 

Considering the irreversible cycle as a totality of an infinite number, n, of irreversible elementary Carnot cycles and taking into account that

 

                                                                            

 

we obtain [see Eq. (3.143)]:

 

                                                                                                                                                                           (3.144)

 

Thus, for an arbitrary irreversible cycle the Clausius integral is always negative.

It should be stressed that this integral pertains to the work done by the system (high-temperature source - working medium - low-temperature heat sink) as a whole. As regards the working medium, its entropy does not change, inasmuch as upon completion of the cycle the working medium returns into its initial state, as was already mentioned above. In other words, for the working medium Eq. (3.116),

 

                                                                                       

 

or, which is the same, the equation

 

                                                                                            

 

is always true.

A question may arise whether there is any contradiction here. Indeed, on one hand, the Clausius integral was shown to be always negative in an irreversible cycle [Eq. (3.144)]; on the other hand, according to Eq. (3.114) this integral is equal to zero. But there is no contradiction here. In Eq. (3.114) the integral refers to the working medium, and the quantity T, present in this equation, is the temperature of the working medium. As regards the Clausius integral present in Eq. (3.144), it pertains, as was already mentioned above, to the system as a whole and, as it is clear from the meaning of the conclusion [see Eq. (3.144)], the temperature present in this equation is the temperature of the heat source, which is not equal to the temperature of the working body in the event of an irreversible process.

Consider now an arbitrary irreversible cycle comprising two processes, an irreversible process 1-2 and a reversible process 2-1 (Fig. 3-18).

 

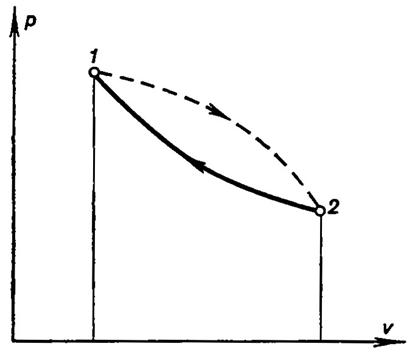
Fig.3.18.jpg

 

 

Fig. 3.18

 

For the cycle considered, the Clausius integral can obviously be presented as the sum of two line integrals:

 

                                                                                                                       (3.145)

 

whence with account taken of Eq. (3.144) it follows that

 

                                                                                                                                 (3.146)

 

For the reversible process 2-1, in accordance with Eqs. (3.115) and (3.117)

 

                                                                   

 

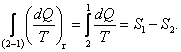
Substituting this expression in the inequality (3.146), we obtain for any irreversible process:

 

                                                                                                                                               (3.147)

 

whence, in the differential form

 

                                                                                                                                                                             (3.148)

 

it should be stressed once more that this relationship holds for any irreversible process proceeding in a system. Consequently, if a reversible process develops in an isolated system (for which, by definition, dQsys = 0), then according to Eq. (3.133),

 

                                                                     

 

The entropy of an isolated system increases as a result of irreversible processes developing in the system.

From the relationship (3.115)

 

                                                                                       

 

it follows that if a reversible process takes place in an isolated system (dQsys = 0), the entropy of the system remains constant:

 

                                                                     

 

No matter what processes proceed in an isolated system, entropy cannot decrease:

 

                                                                                                                             (3.149)

 

[In Eq. (3.149) the equality sign pertains to reversible and the inequality sign to irreversible processes.]

Hence, an important conclusion is drawn (already mentioned above, in Sec. 3.2) that after coming into a state of equilibrium an isolated system remains in this state, i.e. the system is incapable of a spontaneous change of state. Indeed, any spontaneous process is irreversible and, consequently, proceeds with an increase in entropy. The entropy of an isolated system, however, has a maximum value in the state of equilibrium. Consequently, spontaneous processes are impossible in an isolated equilibrium system.

Thus, spontaneous processes continue in an isolated system until the system's entropy reaches its maximum value. Upon reaching the state of equilibrium, for which the entropy is the maximum possible, the spontaneous processes in the system terminate, and the system stays in a state of equilibrium.

Equations (3.115) and (3.148) can be combined in the following form:

 

                                                                                                                         (3.150)

 

Relation (3.150), which is true both for reversible (the sign of equality) and irreversible (the sign of inequality) processes in any system, is the mathematical expression for the second law of thermodynamics. The inequality (3.149) is a particular case of the general inequality (3.150) written for an isolated system (dQsys = 0).