4.1 Basic methods

The combined mathematical expression for the first and second laws of thermodynamics formulated in the preceding chapter has the following appearance:

(4.1)

On the basis of this equation with the aid of mathematical methods we can obtain a number of equations interrelating the various thermodynamic properties of substances.

As was already mentioned, all thermodynamic quantities can be divided into two groups, functions of state and functions of a process. The magnitude of a function of state is determined unambiguously by the properties, or parameters, of a given state. Hence, to determine the change of a function of state, we must only know the values of this function at the beginning and end of the process.

The functions of a process (for instance, work and heat) are determined by the nature of the process causing a change in the state of a thermodynamic system.

As was already mentioned in Chapter 2, the characteristic property of functions of state is that their differential is a total differential. It will be recalled that in mathematical analysis the name total differential of a function of several variables, z = f (x, y, w, . . .), is given to a quantity of the following kind

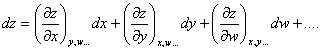(4.2)

In the great majority of cases, in dealing with pure substances we shall consider functions of two variables, z = f (x, y), for which

(4.3)

Partial derivatives are taken on condition that the superscripts put outside the parenthesis are held constant during the differentiation. For instance, the derivative of pressure in respect to temperature, can be calculated for various conditions: on condition of a constant system volume v, on condition that the system's entropy s is constant, or that the system's enthalpy h is constant, etc. In each of these cases the derivative, respectively denoted by etc. will have, generally speaking, a different value. It is known from mathematical analysis that

(4.4)

i.e. the magnitude of a partial derivative of a higher order does not depend on the sequence of differentiation.

From this it follows that if the differential of any function z = f (x, y) is presented in the form

(4.5)

and if it is known that the differential of the function z is a total differential, the following relationship is true:

(4.6)

Equation (4.6) will be used to obtain a number of important differential equations of thermodynamics.

Equation (4.6) can be used, in particular, to show that the differential of a function of a process is not a total differential. Consider, for instance, the expression for the differential of the amount of heat added to a system, i.e. the mathematical formulation of the first law of thermodynamics (2.23),

In order to represent q as a function of two variables p and v, substitute the relationship

for the differential of internal energy. We obtain:

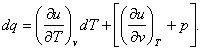(4.7)

We shall now check whether this relationship meets the condition formulated by Eq. (4.6). As applied to Eq. (4.7),

whence

(4.8)

(4.9)

With account taken of condition (4.4) it follows that the condition (4.6) does not apply to equation (4.7): exceeds by . Hence, the differential dq is not a total differential.

A similar conclusion can also be obtained for another function of process, the work of expansion

(4.10)

Expressing this work as a function of two variables, pressure and volume, l = f (p, v), the differential of this function takes the following form:

(4.11)

where x = v and y = p.

Let us check whether the condition (4.6) is satisfied for this function. Comparing (4.10) and (4.11), it is clear that M = p, N = 0 and, consequently,

whence

Thus, the differential dl is not a total differential.

It should be borne in mind that if the path of a process proceeding from state 1 to state 2 is strictly defined, the heat added to the system in the process and the work of expansion done by the system in this process will be determined unambiguously. So, if points 1 and 2 lie on an isotherm, the heat added to the system in the process of isothermal expansion, q₁₂, and the work done by the system in the course of isothermal expansion, l₁₂, can be determined unambiguously if the system's properties for the states 1 and 2 are given. It follows from this that if the properties of state are given for point 1, the quantities q₁₂ and l₁₂ are single-valued functions of the properties of state at point 2.

In this connection it is of interest to consider the concept of heat capacity. In Chapter 1 heat capacity was defined as

Inasmuch as the heat q is a function of a process, in the general form heat capacity is also a function of a process. It was, however, stipulated above that in all instances it shall be specified what heat capacity or which process is involved. Thus the heat capacity is

where x is a constant parameter. In particular, if x = p, then c_x = c_p; if x = v, then c_x = c_v; etc. The heat capacities of concrete processes already possess the properties of functions of state, i.e. in a concrete process heat capacity is determined by the properties of state.

Consider relationship (4.4) applied to the case z = const. Then, dz = 0 and, consequently,

whence

or, which is the same,

(4.12)

It is clear that if a certain quantity z is a function of two variables x and y, z = f (x, y), then, on the same grounds, the quantity x can be considered as a function of the variables y and z, x = φ (y, z), and the quantity y as a function of x and z, y = ψ (x, z). Equation (4.12) relates unambiguously all possible derivatives of these three functions. Equation (4.12) gives for p, v and T the following relations:

(4.12a)

for p, T and s

(4.12b)

for h, u and T

(4.12c)

etc.

Equation (4.3) yields one more useful relationship. Differentiating it with respect to x, on condition that a certain property of state ξ is constant we obtain:

(4.13)

Equation (4.13) permits a relationship to be established between the partial derivatives of one and the same quantities calculated, however, on the basis of different constant parameters.