4.3 Partial derivatives of internal
energy and enthalpy
Consider some of the most important relationships for the partial
derivatives of internal energy and enthalpy. From Eq. (4.14) we obtain:
![]() (4.24)
(4.24)
Substituting into Eq. (4.24) the value of ![]() from Maxwell's
relation (4.23), we find that
from Maxwell's
relation (4.23), we find that
![]() (4.25)
(4.25)
This relationship characterizes the dependence of internal energy on
volume in an isothermal process.
Proceeding as above, we obtain the relationship characterizing the
dependence of internal energy on pressure in an isothermal process:
![]() (4.26)
(4.26)
whence,
with account taken of Eq. (4.22), we find:
![]() (4.27)
(4.27)
Since
![]()
it is
obvious that
![]() (4.28)
(4.28)
and,
consequently, Eq. (4.14) takes the following form:
![]() (4.29)
(4.29)
whence
![]() (4.30)
(4.30)
Taking into account Eq. (4.22), we obtain:
![]() (4.31)
(4.31)
The above relation characterizes the dependence of enthalpy on pressure
in an isothermal process.
Proceeding in a similar manner, we can derive the formula characterizing
the dependence of enthalpy on volume in an isothermal process:
![]() (4.32)
(4.32)
and,
allowing for Eq. (4.23), we obtain:
![]() (4.33)
(4.33)
As was already shown in Chapter 2, one of the properties of an ideal gas
consists in that its caloric quantities are independent of thermal parameters:
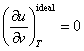 and
and 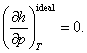
The following "proof” of the independence of the internal energy of
an ideal gas on volume (and, respectively, of enthalpy on pressure) can sometimes
be encountered in the literature devoted to the subject: since from Clapeyron's
equation
![]()
it is clear that
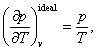
substituting this value of ![]() in equation
(4.25) we get:
in equation
(4.25) we get:
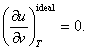
This proof, however, is deceptive. In fact, the dependence of internal
energy u on volume v constitutes, as was already mentioned in
Chapter 2, an independent, special property of an ideal gas and it is not
related in any way to its other property, the property of an ideal gas obeying
Clapeyron's equation. In Chapter 3 the independence of the internal energy of
an ideal gas on volume was used to show that the ideal-gas temperature scale is
identical with the Kelvin absolute thermodynamic scale. It is precisely this
identity that permits us to use Clapeyron's equation in any thermodynamic
calculations. Thus, the fact that ![]() was already
taken into account in Clapeyron's equation when the ideal-gas temperature was
replaced in the equation with the absolute thermodynamic temperature (Sec.
3.5). Consequently, the above "proof” only states once more the
previously known fact.
was already
taken into account in Clapeyron's equation when the ideal-gas temperature was
replaced in the equation with the absolute thermodynamic temperature (Sec.
3.5). Consequently, the above "proof” only states once more the
previously known fact.
The equations derived in this section, especially Eqs. (4.25) and
(4.31), are of paramount importance for thermodynamic studies of the properties
of substances. Making use of the thermal properties of a substance (specific
volume as a function of temperature and pressure), Eqs. (4.25) and (4.31)
permit us to find the caloric quantities, i.e. the internal energy and enthalpy,
and also to solve the reverse problem, i.e. using the known caloric quantities
we can calculate the thermal properties of substances. At a given pressure p
and temperature T the enthalpy of a substance is determined by
integrating Eq. (4.31):
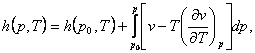 (4.34)
(4.34)
where h
(p0, T) is
the enthalpy of the substance in some initial state, characterized by the same
temperature but by another pressure p0. By
analogy,
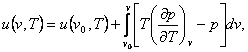 (4.35)
(4.35)
where u
(v0, T)
is the internal energy of the substance in a state characterized by
the same temperature T but by another specific volume v0.
If data on the thermal properties of a substance are available, one can
calculate the integrals present in the right-hand sides of Eqs. (4.34) and
(4.35), with it being necessary then to first calculate the magnitudes of the
derivatives ![]() or
or ![]() . In both cases the integration is performed along an
isotherm.
. In both cases the integration is performed along an
isotherm.
It should be emphasized that Eqs. (4.34) and (4.35) permit us to
calculate not the values of h and u themselves (this problem
cannot be solved by thermodynamic methods alone) but only the difference
between the value of h (or
u) in a given state and
its value in any other state (initial) on the same isotherm.
To solve the reverse problem, i.e. to calculate the thermal quantities
of a substance on the basis of the known caloric properties, we must transform
Eqs. (4.25) and (4.31) in the following way:
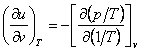 (4.36)
(4.36)
and
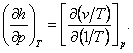 (4.37)
(4.37)
Solving Eqs. (4.36) and (4.37), we obtain, respectively:
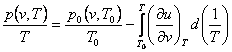 (4.38)
(4.38)
and
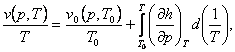 (4.39)
(4.39)
where p0 (v, T0) and v0 (p, T0) are the values of p and
v in some initial state having the same specific volume [as applied to
Eq. (4.38)] or the same pressure [as applied to Eq. (4.39)] as in the unknown
state. It will be noted that the integral in Eq. (4.38) is taken along an
isochor, and the integral in Eq. (4.39) along an isobar. The partial
derivatives of caloric quantities present in the integrands are calculated from
the known caloric properties of the substance.
Equations (4.38) and (4.39) are rarely used in practice, whereas Eqs.
(4.34) and (4.35) find wide application in calculating the thermodynamic
properties of substances.
In conclusion let as calculate some important derivatives of entropy:
![]()
![]()
![]() and
and ![]()
From Eq. (4.14) it follows that
![]() (4.40)
(4.40)
and
![]() (4.41)
(4.41)
and
from equation (4.29) we get:
![]() (4.42)
(4.42)
and
![]() (4.43)
(4.43)