4.4 Heat capacities

Since

   and   

we can write

                                                         (4.44)

In particular, for the heat capacity at constant pressure,

                                                         (4.45)

Since, as can be seen from Eq. (4.29), for an isobaric process (p = const)

we have

                                                          (4.46)

Analogously, for the heat capacity at constant volume,

                                                         (4.47)

With account taken of the fact that, as can be seen from Eq. (4.14), in an isochoric process (v = const)

we obtain from Eq. (4.47):

                                                          (4.48)

The set of differential equations of thermodynamics permits the establishment of a number of important relations for heat capacities.

Differentiating

with respect to temperature at p = const, we obtain:

                                             (4.49)

To pass from the partial derivative  to the derivative  make use of Eq. (4.13):

                                          (4.50)

Using the relationship (4.25), we get:

                                    (4.51)

Substituting Eq. (4.51) into relation (4.49), we find that

                                                (4.52)

With the aid of Eq. (4.12a), the important equation (4.52) that relates the constant-pressure (isobaric) and constant-volume (isochoric) heat capacities, c_p and c_v, can also be presented in two forms:

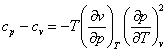                                                (4.53)

or

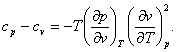                                              (4.54)

For an ideal gas,

   and   

consequently,

Equation (4.45) can be rewritten in the following way:

Applying Maxwell's relation (4.20), we obtain:

                                                   (4.55)

Analogously, for the constant-volume heat capacity Eq. (4.47) yields

whence, with account taken of Maxwell's relation (4.21), we obtain an equation relating the constant-volume heat capacity c_v and the derivative ,

                                                  (4.56)

The relation expressing the dependence of c_p on pressure, i.e. the quantity  is found by differentiating Eq. (4.31) with respect to temperature at p = const:

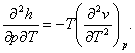
Since the sequence of differentiation does not effect a higher-order derivative,

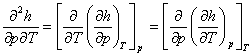
and, consequently,

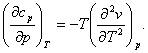                                                  (4.57)

By analogy, from (4.25) we can derive the equation for the dependence of the constant-volume heat capacity, c_v, on volume:

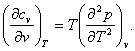                                                    (4.58)

In conclusion, let us formulate one more essential thermodynamic equation, which relates the quantities c_p and c_v. Dividing (4.55) by (4.56), we get:

                                                    (4.59)

Combining equations (4.59) with (4.52), we get the following two relations:

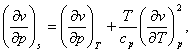                                             (4.60)

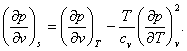                                             (4.61)