5.3 Conditions of stability and
equilibrium for an isolated homogeneous system
Thermodynamic methods make it possible to show that if a system is in
the state of thermodynamic stability, the following relationships must be
satisfied for any substance:
(5.63)
and
(5.64)
i.e. in
the first place, the isochoric (constant-volume) heat capacity cv is always positive and, in
the second place, in an isothermal process an increase in pressure always
results in a decrease in the volume of substance. The condition (5.63) is
called the condition for thermal stability, and the condition (5.64) is
referred to as the condition for mechanical stability.
The conditions (5.63) and (5.64) can be elucidated by the so-called Le
Chatelier principle, which
states that:
If a system is
subjected to a constraint whereby the equilibrium is modified, a change takes
place, if possible, which partially annuls the constraint.
These conditions for thermodynamic stability of a system are clear and
require no formal derivation. Imagine the heat capacity cv of
some substance to be negative. This would mean that, since
isochoric
addition of heat would result not in an increase but in a decrease in
temperature. This would mean that the more heat added to the substance
undergoing an isochoric process, the greater the difference between the
temperatures of the substance and the heat source (surroundings). As a result
of the increase in the difference between the temperatures of the substance and
surroundings, the whole system (i.e. the substance and the heat source)
would continue to deviate from the state of equilibrium instead of tending to
reach it, with the process developing at an ever increasing rate[1].
Thus, the system would be unstable: even a negligible difference in the
temperatures of the substance and the surroundings would cause an
avalanche-type increase in the system's lability. On the other hand, similar
reasoning for the case when cv > 0 brings us to the
logical conclusion that heat transfer between the substance considered and the
surroundings, accompanied by an increase in substance temperature, will cease
when the temperatures of the surroundings and substance become equal, and a
state of equilibrium establishes in the system.
The validity of the condition (6.64) can be assured as follows. Assume
that for a substance
(5.65)
which
means that with an increase in volume the pressure in the substance will rise.
Just as before, consider a system consisting of two components, the substance
and the surroundings; there is heat transfer between the substance and the
surroundings, in the course of which the temperatures of the two constituents
are the same. Let the pressure of the substance increase in respect to the
pressure of the surroundings by an infinitesimal value. This will clearly
result in a certain expansion of the substance, and the volume of the
surroundings will decrease (they will contract). However, in accordance with
condition (5.65), this will cause a further increase in the pressure of the
substance considered, which, in turn, will be accompanied by an increase in the
volume of the substance, etc. Proceeding at an ever increasing rate, the
process will lead to a limitless expansion of the substance at an infinitely
large increase in the substance pressure. If we consider another case when the
initial pressure of the substance is somewhat lower than the pressure of the
surroundings, similar reasonings will lead us to the conclusion that an
avalanche-type decrease in the volume of the substance with a drop in substance
pressure is inevitable.
Thus, in both cases the system considered will be unstable.
On the other hand, if
and if
the pressure of the substance investigated exceeds the pressure of the
surroundings, an expansion of the substance will lead to a decrease in its
pressure until the pressure of the substance and that of the surroundings
become equal, i.e. until the system reaches a state of equilibrium.[2]
Let us proceed now to consider the conditions for the equilibrium in
thermodynamic systems.
Of the variety of thermodynamic systems differing from each other in the
various modes of interactions (conjugation) with the surroundings, of the
greatest practical interest are the conditions for equilibrium in an isolated
thermodynamic system.
Consider such an isolated system, illustrated in Fig. 5.1. Imagine this
system divided into two parts (sometimes referred to as two subsystems) 1 and
2 and find the conditions for equilibrium between the two subsystems.
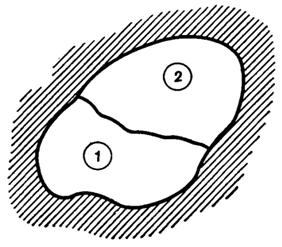
Fig. 5.1
Inasmuch as the system as a whole is said to be isolated, Vsys = const and Usys = const.
At the same time consider an infinitesimal process proceeding inside the
isolated system such that it causes either a change in the volume of each of
the subsystems or a change in the internal energy of the subsystems or a change
in both volume and internal energy. Let the volume of the first subsystem
change by dV1, and the
internal energy by dU1
and the volume and internal energy of the second substance by dV2 and dU2, respectively. Inasmuch as the
volume and the internal energy of the entire system remain constant, dV1 = - dV2 and dU1=
- dU2; in other
words, the change in the volume (or internal energy) of the
first subsystem is equal to the change in the volume (or internal energy) of
the second subsystem.
Previously, an important equilibrium criterion was established for an
isolated system: the entropy of an isolated system in thermodynamic equilibrium
was shown to preserve a constant (maximum) value, i.e. in a state of
equilibrium
(5.66)
Since entropy is an additive quantity, for the case under consideration,
(5.67)
and in
accordance with Eq. (5.66),
(5.68)
From equation
it
follows that
(5.69)
Thus, for subsystem 1,
(5.70)
and for subsystem 2,
(5.71)
In accordance with Eq. (5.68), we get:
(5.72)
Equation (5.72) can be presented in the following form:
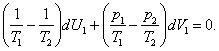(5.73)
It was mentioned above that the volume and internal energy of each of
the subsystems can change independently from each other, i.e. a process is
possible in the course of which the volume of each subsystem changes and their
internal energies remain unchanged and, vice versa, a change in the internal
energy of the subsystems may not cause a change in their volumes. In other
words, the differentials dV1
and dU1
are independent, in principle. Then, for the left-hand side of Eq. (5.73)
to be equal to zero, the coefficients of the differentials dV1 and dU1, present in this equation, should be independently equal
to zero, i.e. it is required that
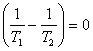(5.74)
and
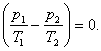(5.75)
From (5.74) we obtain:
(5.76)
and
from Eq. (5.75), allowing for Eq. (5.76), we get:
(5.77)
We shall, obviously, come to the same conclusion, irrespective of the
number of subsystems into which the system is imagined to be divided. Thus, we
arrived at the conclusion that in equilibrium the temperature and pressure are
the same in all parts of an isolated system.
The question arises of whether the obtained conclusion is valid for any
isolated system or whether in deriving it some simplifying assumptions,
restricting the sphere of application of this conclusion, were made.
In fact, a number of restrictions was admitted. Firstly, the combined
mathematical statement of the first and second laws of thermodynamics was used
not in its most general form
but in
the form
(5.78)
i.e. we
restricted ourselves to considering the case when the only kind of work done is
the work of expansion. If we considered other kinds of work (for instance, a
system placed in a potential field; an example is a gas in a gravitational
field), we would have other conditions for the equilibrium of a system. It is
also easy to find that condition (5.76), requiring that the temperature be the
same over the entire volume of a system, would remain unchanged, and only
condition (5.77) would change. For instance, for a gas placed in a
gravitational field it would follow that the pressure in the column of the gas
would increase with diminishing height.
Secondly, we assumed that there exist no peculiarities for the interface
separating the two subsystems which should be taken into account. This
assumption is not valid when a substance is in different phases in the
subsystems; strictly speaking, account should be taken of the surface layer,
which, as it will be seen below (Sec. 5.9), has a number of special properties.
One more member must then be added, and that is the energy of the surface
layer. It will be noted, however, that condition (5.76) will then remain
unchanged. As regards condition (5.77), for the case with a flat interface this
condition will also remain unchanged; but if the interface is a curved surface,
condition (5.77) will be replaced by another one (see Sec. 5.9).