5.4 Conditions for phase
equilibrium
Considering in the preceding section the conditions for equilibrium in
an isolated single-phase system, we found that the temperature and the pressure
are the same in all parts of the system. Now, examining isolated systems
consisting of two (or more) phases, let us find the general conditions for
phase equilibrium.
In considering an isolated thermodynamic system consisting of two subsystems
1 and 2, let us
use the method followed in the preceding section. The difference will be that
now the substance is in two different phases, and the amount of substance in
the subsystems can change due to the transfer of substance from one phase into
the other.
Thus, for the system considered, Vsys
= const, Gsys = const, and
Usys =
const; here, Gsys
is the total quantity of substance in the system. Such a system can be
visualized, for instance, as a constant-volume vessel with ideal
heat-insulating walls, with one part of the vessel being filled with water, and
the other, the upper part, with water vapor.
Hence,
(5.79)
(5.80)
(5.81)
where
the subscripts 1 and 2 refer to the first and second phases,
respectively.
As it can be seen, in contrast to the previously considered isolated
homogeneous system, here, in addition to V and U, the quantity of substance in each
of the subsystems (phases) considered is also taken account of.
It follows that
(5.82)
(5.83)
(5.84)
and,
just as before,
and
Consequently,
(5.85)
Let us consider now the expression for the total differential of the
entropy of subsystem 1. It is clear that the entropy of this subsystem, S1, must be considered not only as a function of the
subsystem's volume V1 and
its internal energy U1
as was the case for a single-phase system, but also as a function of the
amount of substance in the subsystem, G1,
i.e. S1 =
f (V1, U1, G1). Accordingly,
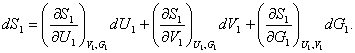(5.86)
As it was shown above [see Eq. (4.40)[1]],
Accordingly, Eq. (5.86) takes the following form:[2]
(5.87)
By analogy, for the entropy of subsystem 2 we have:
(5.89)
Substituting the expressions derived for dS1 and dS2 into Eq. (5.85) and
allowing for the relationships (5.82) through (5.84), we obtain:
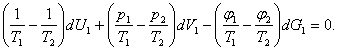(5.90)
Since the differentials dU1, dV1
and dG1 are mutually independent (on the
ground of the reasonings of the preceding section, i.e. of the independence of dV1 and dU1), for the left-hand side of Eq. (5.89) to be equal to
zero, the coefficients of dU1
dV1 and dG1 must be equal to zero,
i.e.
(5.91)
(5.92)
(5.93)
The first two relationships yield the already known conditions:
and
and Eq.
(5.93) provides a new condition
(5.94)
Thus, if two phases are in equilibrium, the temperatures, the pressures,
and the chemical potentials of these phases are the same. Proceeding in similar
manner, we get the same result for a system with more than two phases.