5.5 Phase changes
By a change of phase, or
phase transition, we
mean the transition of a substance from one phase to another phase that
coexists with the first. Speaking of the phases of a pure substance, we usually
have in mind the states of aggregation of substance and therefore, we talk of
the gas, liquid and solid phases. Strictly speaking, however, the concept of a
phase is somewhat narrower than the concept of the state of aggregation: some
substances (for instance, ice) have three solid phases. Nevertheless (unless
otherwise stated), by the change of phase, or phase transition, we shall mean
the transition of a substance from one state of aggregation to another.
Everyday experience shows that one and the same substance can exist in different
states of aggregation, depending on external conditions (pressure and
temperature). At atmospheric pressure, for instance, water exists in the liquid
state at temperatures ranging from 0 to 100 °C. At a temperature below 0 °C and
at atmospheric pressure water passes into its solid phase, ice, and upon
heating to a temperature above 100 °C it passes into the vapor state. It is
also known that the solidification and boiling points of a substance change
with pressure.
In different states of aggregation the physical properties of a
substance differ, which is the case with the density of a substance, in
particular. This difference is traced to the nature of intermolecular
interaction. We shall confine ourselves to a simplified treatment, based on the
phenomenon of association, i.e. on the formation of complexes of a greater or
smaller number of molecules. With a change from the solid to the vapor phase,
or with a solid-vapor phase change, the heat of phase transition is expended
both to perform compression work and to overcome the intermolecular forces, i.e.
to destroy the molecular complexes, the phenomenon being accompanied by a
decrease in the density of the substance. When the change of phase involves
melting or sublimation, the heat of phase transition is spent to destroy the
crystal lattice of the solid, undergoing a change of phase.
Vapor-phase association progresses with rising pressure. Since the
liquid phase is under a rather high internal pressure, the decisive factor here
is not pressure but temperature, and the association diminishes with the rising
of the temperature. That is why a rise in temperature and pressure is accompanied
by a decrease in the heat of vaporization.
The solid-vapor phase change, proceeding under very low pressures, is called
sublimation. From the foregoing it follows that the heat of sublimation must
be rather great (greater than the heat of melting or the heat of vaporization).
A change of phase usually involves an abrupt change in the density of a
substance, with the density of the vapor phase being always smaller than the
density of the condensed phase[1]
in the event of vaporization and sublimation. As regards melting, various cases
are possible for different substances: the density of the solid phase may be
either greater or smaller than the density of the liquid.
Phase transition points are classified as follows: the liquid-vapor phase
transition point is called the boiling point (also referred to as the condensation
point), the solid-liquid phase transition point is known as the melting
point (or the solidification point), and the solid-vapor phase
transition point is referred to as the sublimation point.
For a given substance and for each value of the temperature at a given pressure
there exists in the liquid or vapor phases a definite composition of the
molecular associations. The higher the temperature at a given pressure, the smaller
these associations are. But this does not mean that for each temperature there
exist associations of only one size: at any temperature there coexist
associations of a different size, but the higher the temperature, the greater
the number of small associations and the smaller the number of large associations
in a phase.
Thus, a rise in temperature is accompanied by a certain break-up of the molecular
associations (disintegration of crystals in the solid phase). This process is
markedly speeded up near the transition points in which there is an abrupt
change in the molecular structure of substance.
Some substances, existing in the solid state, can form not one but
several crystalline modifications (for instance, the allotropic modifications
of ice). Each of these modifications exists in its own region of properties of
state, and if these properties change, the modification changes to another one.
Each of these modifications is a phase; the change from one phase to another is
accompanied by the addition (or removal) of the heat of transition and by a corresponding
change in the substance density. In a solid different phases are frequently
encountered, and examples of the existence of different phases in a solid will
be treated in Sec. 6.1.
In analyzing phase equilibrium and change-of-phase processes, the so-called
Gibbs phase rule is of paramount importance. It establishes the relation
between the number of intensive variables that can be varied independently, the
variables which determine the state of a thermodynamic system in equilibrium
(these variables are often referred to as the degrees of freedom of a system), the number of phases, and
the number of components[2].
The phase rule may be stated as
![]() (5.95)
(5.95)
where ψ
is the number of degrees of freedom (or intensive variables) that can be varied
independently in a thermodynamic system, n is the number of components
in the system, and r is the number of
phases in the system.
The phase rule, which is true for systems with any number of components,
is of paramount importance in chemical thermodynamics. As applied to a pure
substance (a single-component system, n = 1), the phase rule acquires the
following form:
![]() (5.96)
(5.96)
From Eq. (5.96) it follows that for pure substances in a single-phase system
(r = 1) the number of degrees of
freedom (or the number of intensive variables that can be varied independently)
ψ = 2. Such independent variables may be p and T, for instance. This means that if,
in dealing with such a system, pressure and temperature are given arbitrarily,
then all other intensive parameters of the system, such as specific volume,
entropy, enthalpy, etc., will be determined unambiguously. Thus, any three
intensive thermodynamic quantities determining the state of a given substance
(for instance, p, T and
V) present a group of
variables, two of which can be varied independently, and the third is a
function of these two variables.
Consider a system, which consists, as before, of a pure substance, but
containing not one but two phases which are in equilibrium with each other. Since
for this case r = 2, the system
possesses only one degree of freedom, meaning that either pressure p or
temperature T, for
instance, can be the independent variable, determining fully the state of
equilibrium for each phase of the system. This conclusion is of great
importance. Indeed, .if the temperature at which a phase transition takes place
is known, it determines unambiguously all other intensive thermodynamic
quantities for each of the phases involved, i.e. the pressure at the transition
point, the density of the substance in each of the coexisting phases, specific
enthalpies and entropies, etc.
The phase transition boundary can be represented on a p-T diagram
if we plot the state corresponding to the pressures and temperatures at which
the change of phase takes place.
Considering a single-component three-phase system (r = 3), we find that the number of the degrees of freedom of this
system is zero, this meaning that in a single-component system three phases may
be in equilibrium only at a definite temperature and pressure, specific to the
given substance. On the p-T diagram, the state in which the three phases
coexist will be represented on the phase boundary line by a point (the
so-called triple point). The
triple point, most typical of a pure substance, is that at which the solid,
liquid and vapor phases coexist. For water the triple point corresponds to a
temperature of 0.01 °C and a pressure equal to 610.8 Pa (0.006228 kgf/cm2).
It was mentioned above that some substances may have more than one phase in
their solid state. Substances of this kind can obviously have several triple
points. The triple point at which a substance exists in three states of
aggregation is sometimes referred to as the principal triple point.
Depicted in Fig. 5.2 is a typical p-T diagram for a substance, on
which phase boundaries are drawn. The region of the solid phase of the
substance is arranged to the
left of boundary line AOB. The vapor-phase region is arranged to the
right of boundary line COB, and
the liquid-phase region is found between the boundary lines OA and OC.
It is clear that having available the p-T diagram of a substance, we
can always determine whether the substance is in the solid, the liquid or the vapor
state at any pressure p and temperature T. From the p-T diagram
it follows that line OB represents the sublimation boundary for
the substance, line OA, the melting, or solidification
boundary, and line OC the boiling, or condensation
boundary. The boiling boundary is usually called the saturation
boundary. Point O is the triple point at which the substance
coexists in the three states of aggregation.
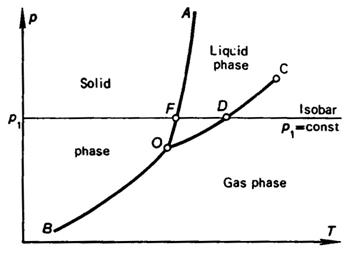
Fig. 5.2
The sublimation boundary runs down towards the low temperatures region. The
melting boundary rises to the region of higher pressures; latest investigations
show that the melting (solidification) boundary does not terminate even at
ultrahigh pressures (of the order of tens of thousands to hundreds of thousands
of atmospheres). The saturation line OC terminates at point C, referred
to as the critical point. Inasmuch as the properties of various substances
differ, the p-T diagrams of different substances differ as well.
From Fig. 5.2 it can be seen that the slope of the sublimation boundary
and of the saturation line is positive. This means that the temperature of
phase-transition (sublimation and boiling) temperature rises with the increase
in pressure. This regularity holds for all pure substances
known. The slope of the solid-liquid phase boundary for different substances
may be either positive or negative.
It is also clear from the p-T diagram shown in Fig. 5.2 that the
state of a substance changes upon heating at a constant pressure. Moving along
the isobar p1 = const from the solid-phase region, we cross
the solid-phase boundary at point F; the substance changes its phase from solid into liquid. If the
heating is continued, we cross the saturation line OC at point D; the substance turns into vapor.
Further advance along the isobar p1 = const to the region of higher temperatures
corresponds to heating the substance in the vapor (gas) phase. As an
illustration, let us present the p-T diagrams for water (Fig. 5.3) and
carbon dioxide (Fig. 5.4). The negative slope of the melting, or solid-liquid,
boundary is distinctly seen in the first p-T diagram (Fig. 5.3a is drawn on a smaller scale than Fig.
5.3b).
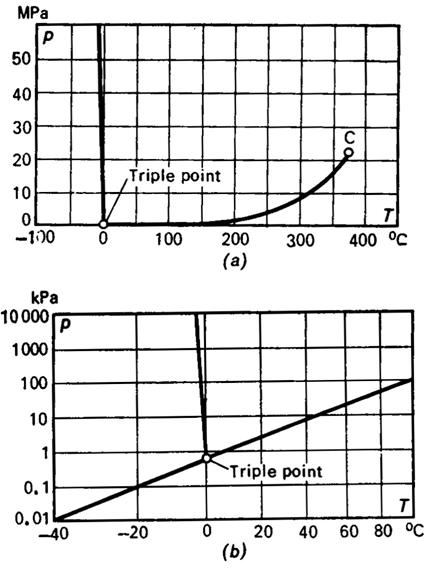
Fig. 5.3
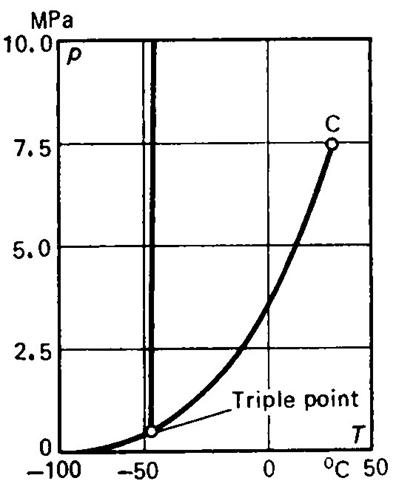
Fig. 5.4