5.7 Phase stability

 

Let us dwell on some problems pertaining to phase stability.

Consider the dependence of the chemical potential of a substance on the pressure of each of the two phases at constant temperature. A dependence of this kind is shown graphically in Fig. 5.6. Since

 

                                                               

 

in Fig. 5.6 the curve 1 pertains to the phase with a greater density (smaller v), and curve 2 to the phase with a smaller density. It will also be noted that in the φ and p coordinates the convexities of the isotherms are always facing upward, since, as it is clear from Eq. (5.99),

 

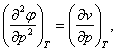                                                                                                               (5.127)

 

and the quantity (dv/dp)T, according to Eq. (5.64), is always negative.

 

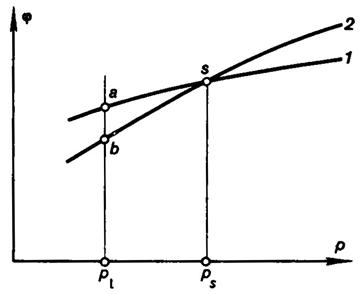
Fig. 5.6.jpg

 

Fig. 5.6

 

Assume that curve 1 pertains to the liquid phase (φl), and curve 2 to the saturated-vapor phase (φv). It is clear that point s, at which the curves 1 and 2 intersect, i.e. at which φ1 = φ2, is the point of phase equilibrium for the given substance (the pressure is ps).

In accordance with the additivity rule, the expression for the isobaric-isothermal potential of a two-phase system can evidently be written as

 

                                                                                                             (5.128)

 

Consider a system, comprising two phases at the same pressure and temperature[1] (points a and b on the isobar p1 Fig. 5.6). If this state is not a state of equilibrium for the system considered, hence this isobaric-isothermal system is capable of undergoing a process leading to a change in the system potential Φ. Since the pressure and temperature are constant, it is clear that φl and φv remain constant during this process, so that dφl = 0 and d φv = 0. It follows that the quantity Φsys can change only at the expense of Gl and Gv, and from Eq. (5.127) we obtain:

 

                                                                                                       (5.129)

 

At the same time it is known that

 

                                                                                                       (5.130)

 

and, consequently,

 

                                                                                                                       (5.131)

 

Equation (5.129) acquires then the following form:

 

                                                                                                         (5.132)

 

Since in the process of coming into equilibrium the potential Φ of an isobaric-isothermal system always diminishes, tending to a minimum (see Sec. 5.2), i.e. dΦsys < 0, the sign of the differential dGv is determined by the sign of the difference (φv - φl).

From Fig. 5.6 it is clear that to the left of point s, i.e. at p < ps we have • φv < φl and, consequently, dGv must be greater than zero. This means that in this system there will be mass transfer from the liquid phase to the vapor phase. To the right of point s, i.e. at p > ps, φv < φl and, consequently, dGv < 0; there is mass transfer then from the vapor phase into the liquid phase. Thus,

if φv > φl, then dGv < 0 and, consequently, the stable state of the system is the liquid state;

if φv < φl, then dGv > 0 and, consequently, the stable state of the system is the vapor phase.

The foregoing permits the unambiguous conclusion that with given p and T, the more stable of the two phases is the phase whose chemical potential is smaller.

 


[1] It will be shown that under certain conditions the existence of the so-called meta-stable states of substance is possible (the concept of such a state was introduced in Sec. 5.1), i.e. states in which, for instance, vapor can be cooled at a given constant pressure to a temperature below the condensation point (so that no condensation would take place) or liquid can be heated to a temperature above the boiling point or liquid can be cooled below the solidification temperature. This fact permits us to consider a liquid and a vapor existing simultaneously at a pressure exceeding somewhat (or lying somewhat below) the saturation pressure at the given temperature, ps i.e. curves 1 and 2 exist to the left and to the right of point s in Fig. 5.6.