5.8 Phase changes at unequal phase pressures

 

Consider the conditions of phase equilibrium for the case when each of the two coexisting phases is at a different pressure. Such cases are not infrequent in practical applications, for instance, the case of an inert gas exerting pressure on a liquid at such a temperature that vapor pressure on the top of the liquid is comparatively low. It is clear that the vapor can then be considered with a good degree of approximation as an ideal gas, whose properties are in no way affected by the presence of the inert gas. On the other hand, the inert gas transmits its pressure to the liquid. Thus, the liquid and its vapor will be under a different pressure.

Let us determine the conditions for thermodynamic equilibrium in an isolated system with unequal phase pressures. Consider the case of liquid-vapor equilibrium when the supplementary pressure on the liquid is provided by an inert gas. (The results can be shown to be valid also for cases when the supplementary pressure is created by other methods.)

This system can be visualized in the form of a closed heat-isolated vessel with rigid walls, with two phases of a substance, the liquid phase and the saturated vapor phase. On the top of the liquid there is not only the vapor phase but also the inert gas, imparting an additional pressure p* on the liquid. It will be emphasized that the behavior of the vapor and of the inert gas complies with Dalton's law.

Analyzing the conditions for phase equilibrium in such a system with the aid of the method applied in Sec. 5.4, we can easily obtain the following relations for phase equilibrium in a system characterized by unequal phase pressures:

 

                                                                                                                               (5.133)

 

                                                                                                                               (5.134)

 

                                                                                                                     (5.135)

 

The relations, or conditions, (5.133) and (5.134) are in agreement with the previously derived conditions (5.76) and (5.94). The condition (5.135) also stands to reason: the difference between the pressures of the two coexisting phases is equal to the supplementary pressure exerted on one of the phases.

These conditions are true not only for the case of liquid-vapor equilibrium, but also for other cases of phase equilibrium, such as solid-liquid and solid-vapor equilibrium.

Consider now the following interesting problem. Will the pressure on the second phase change (and to what extent) if the pressure on the top of the first phase changes, on condition that the temperature is constant and equilibrium is preserved?

Consider a two-phase system. Let the initial phase pressures be equal to p0 and assume that the system is in thermodynamic equilibrium. It is clear then that

 

                                                                                                          (5.136)

 

Let the pressure exerted on the first phase increase by dp1, with the temperature T remaining constant. Assume that thermodynamic equilibrium sets in again between the two coexisting phases, with the pressure of the second phase changing by dp2 (we do not know whether dp2 is equal or not equal to zero). If the two phases are in equilibrium, it is clear that

 

                                                                                       (5.137)

 

Expanding the function φ (p + dp, T) into the Taylor series, we obtain:

 

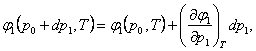                                                                            (5.138)

 

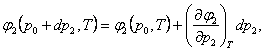                                                                          (5.138)

 

and, taking into account that  Eq. (5.137) reduces to

 

                                                                                  (5.140)

 

With account taken of (5.136), from Eq. (5.140) we find that

 

                                                                                                                     (5.141)

 

whence

 

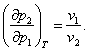                                                                                                                     (5.142)

 

This important equation, first derived by the English physicist J. H. Poynting, leads us to an unexpected result, showing that if the pressure of one of the phases of the equilibrium system increases, the pressure of the other phase will also increase, with the increase in the pressure of the second phase being as many times smaller (or greater) as the specific volume of the second phase is smaller (or greater) than the specific volume of the first phase.

So, for instance, if the liquid is subjected to the supplementary pressure exerted by an inert gas, the pressure of the saturated vapor of this liquid will increase. If pressure is exerted upon a solid phase which is in equilibrium with a liquid, liquid phase pressure will rise as well.

Since at low pressures (considerably lower than the pressure at the critical point) the density of a vapor is much smaller than the density of a liquid, an increase in the liquid phase pressure is accompanied by a slight increase in the vapor phase pressure. (For instance, the specific volume of water at atmospheric pressure v' = 0.001 m3/kg, the specific volume of vapor v" = 1.7 m3/kg and, consequently, Δp"  0.0006 Δp'.) Things are different for solid-liquid equilibrium: since the densities of solid and liquid phases are of the same order of magnitude, the values of Δp1 and Δp2 are practically the same (so, for water at atmospheric pressure vw = 1.00 cm3/g, and for ice vice = 1.09 cm3/g; hence, Δpw  1.09 Δpice).

It should be emphasized that Poynting's equation is valid only for the case when T = const. In other words, if the pressure exerted on one of the phases in equilibrium rises, the pressure in the other phase will increase only if the temperatures of the coexisting phases remain constant. But if no such limitation is imposed, then an increase in the pressure exerted on one of the phases should not be necessarily accompanied by a change in the pressure of the second phase (the system has now an extra degree of freedom). This case of phase equilibrium is described by Eq. (5.152) given below.

One more important fact must be noted. If the two phases were under the same pressure p0, and then the pressure of one of the phases was increased to p1, the difference between the two pressures acting now on the two-phases, p*, should not be taken to be equal to (p1 - p0): in accordance with Poynting's equation, the pressure in the other phase must also inevitably increase (to p2 > p0) and, consequently, the difference p* = p1 – p2 will always be smaller than the supplementary pressure exerted on the first phase (p1 - p0).

The quantities p1, p2, p* and p0 can be easily related.

In accordance with the foregoing, it is clear that

 

                                                                                                                   (5.143)

 

where Δp1 = p1 - p0 and  Δp2 = p2 - p0 represent the increase in the pressure of each phase due to a rise in the pressure of the first phase to p1. In accordance with Poynting's equation,

 

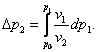                                                                                                                   (5.144)

 

If the ratio v1/v2 is not affected greatly by a change in p1 (which is usually true), then it can be assumed with a good approximation that

 

                                                                                                                      (5.145)

 

With account taken of (5.145), Eq. (5.143) takes the form

 

                                                                                                                   (5.146)

 

or, which is the same,

 

                                                                                                                 (5.147)

 

This implies that

 

                                                                                                           (5.148)

 

and

 

                                                                                                         (5.149)

 

Equations (5.148) and (5.149) relate p1, p2, p* and p0.

Let us find the temperature derivatives of the unequal pressures p1 and p2 of the coexisting phases, making use of the method previously employed in deriving the Clausius-Clapeyron equation.

In accordance with Eq. (5.134), for phases in equilibrium

 

                                                                                                           (5.150)

 

Change the temperature of each phase by dT, the pressure of the first phase by dp1, and the pressure in the second phase by dp2. If the change in temperature causes a change in the pressures p1 and p2 such that the phases considered remain in equilibrium, it is clear that under these new conditions the chemical potentials of the phases involved will be equal to each other:

 

                                                                       (5.151)

 

Expanding the functions in this relation in Taylor series (5.98) and taking Eqs. (5.99), (5.100), (5.106) and (5.150) into account, from equation (5.151) we obtain:

 

                                                                                                           (5.152)

 

This important relation, similar to the Clausius-Clapeyron equation, relates the temperature derivatives of the pressures of two phases coexisting at different phase pressures. If the pressures of the coexisting phases are the same, Eq. (5.152) reduces to the conventional Clausius-Clapeyron equation (5.107). If T = const, this equation takes the form of and becomes Poynting's equation (5.142).