5.9 Phase changes under curved
surfaces
When the interface is not a flat surface but a curved one, a pressure
difference due to surface tension appears between the phases.
It is known from elementary physics that the so-called surface
tension acts at the interface, the force tending to reduce the area of
liquid at the interface to a minimum. It will be recalled that by definition
the surface tension a is the name given to the force acting on unit
length of the perimeter of the area; these forces, normal to the perimeter and
tangent to the interface, are depicted by arrows in Fig. 5.7, which shows an
elementary section of an interface. Since with a flat interface the surface
tension forces, acting at all points of the perimeter of the section (Fig.
5.7a), lie in one plane, the resultant of these forces is evidently zero.
Things are different with a curved interface. As can be seen from Fig. 5.7b, the surface tension forces, acting at
various points of the perimeter, lie in different planes, and their resultant
is no more equal to zero, the resultant evidently being the larger the greater
the curvature of the phase interface is. It can be easily seen that the
resultant force acts in the direction of the concave side of the curved
surface. Thus, the phase under the concave side of the interface will be
affected by an additional pressure due to surface tension.
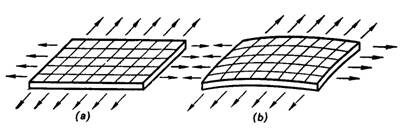
Fig. 5.7
Let us find how this force is related to the magnitude of the surface
tension and to the curvature of the interface. Consider a small square on the
curved surface (Fig. 5.8), and calculate the resultant of the surface tension
forces acting on the sides AB and CD of the perimeter. The force
acting on side AB is
![]() (5.153)
(5.153)
where lAB
is the length of side AB. By analogy, the force acting on side CD
is
![]() (5.154)
(5.154)
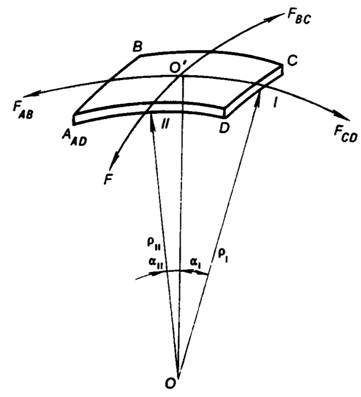
Fig. 5.8
The resultant of the forces FAB and FCD is the sum of the
projections of the vectors representing FAB and Fcd on the line OO', which is normal to the section of the
surface at its centre. This resultant force is equal to
![]()
where
αI is the angle between the normal OO' and the radius of
curvature of our section of the interface, in the plane of the square with the
sides AB and CD ,drawn to point I. Inasmuch as
![]() (5.155)
(5.155)
it is clear that
![]() (5.156)
(5.156)
and, consequently, the resultant of the forces FAB
and FCD will be
![]()
Analogously, the resultant of forces FAD
and FBC will be
![]()
where an is the angle between the normal OO' and
the radius of curvature of our section of the interface, in the plane of the
square with the sides AD and BC, drawn to point II.
Hence, the resultant of the forces FAB,
FBC, FCD, FAD,
i.e. of all surface tension forces acting on the section of the interface,
will be equal to:
![]() (5.157)
(5.157)
As can be seen from Fig. 5.8,
![]() and
and ![]() (5.158)
(5.158)
With account taken of relationships (5.158),
Eq. (5.157) takes the following form:
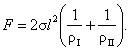 (5.159)
(5.159)
Dividing the force F by the area of the
section considered (this area can easily be seen to be l2), we obtain the magnitude of the supplementary pressure
due to surface tension forces:
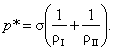 (5.160)
(5.160)
This equation, first derived by Laplace,
relates the difference between phase pressures with surface tension and the
curvature of the interface (it will be noted that the Laplace equation can also
be derived in a purely thermodynamic way).
Present in Laplace's equations are two radii
of curvature ρI and ρII. This can be easily
justified. From analytic geometry it is known that the curvature of a surface
is characterized by two radii that determine the curvature of this surface in
two mutually perpendicular cross sections.
The curvature of an interface will be assumed
to be positive when the phase of a greater density is arranged on the concave
side of the interface, and negative when this phase lies on the convex side of
the interface.
It follows from the Laplace equation that for
a flat interface (i.e. for an interface whose radius of curvature is infinitely
large) the supplementary pressure p* is equal to zero, as could be
expected.
The curvature of a spherical interface is the
same in any section:
![]() (5.161)
(5.161)
where ρ is the radius of the sphere. From Eq.
(5.161) it is clear that for a sphere the Laplace equation takes the form
![]() (5.162)
(5.162)
Consider a spherical drop of liquid in equilibrium with its saturated
vapor at some temperature T0.
If the liquid-vapor interface (or boundary) were flat, the pressure of the liquid
would be equal to the vapor phase pressure; this would be the pressure p0, the saturation pressure at temperature T0. However, for a
spherical drop, the liquid phase is acted upon by a supplementary pressure due
to surface tension forces. According to Poynting's equation (see Sec. 5.8), the
presence of the supplementary pressure will cause an increase in the vapor
phase pressure. If liquid phase pressure is denoted by pl, and the pressure of the vapor in the space above the
drop of liquid by pv, then
from Eqs. (5.148) and (5.149) it follows that for the case considered (a drop
with radius ρ) we have:
![]() (5.163)
(5.163)
![]() (5.164)
(5.164)
If vapor pressure is low and, consequently, the specific volume is large
compared with the specific volume of the liquid, so that the value of vl can be ignored in
comparison with vv, these equations can be presented in
the following form:
![]() (5.165)
(5.165)
![]() (5.166)
(5.166)
Finally, if vapor pressure is so low that the vapor can be considered as
an ideal gas, then
![]()
and,
consequently, from Eq. (5.166) we obtain:
![]() (5.167)
(5.167)
whence
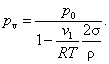 (5.168)
(5.168)
Taking account of surface tension forces is essential in analyzing
various phase change processes proceeding in the presence of a curved phase
interface.