7.3 The isothermal process
The isotherms of a real gas are plotted in the p-v, p-T, v-T, T-s diagrams
of state shown in Fig. 7.5. If the parameters, or properties, of one state are
known, then the parameters of another state, lying on the same isotherm, can be
determined if one more parameter is known.
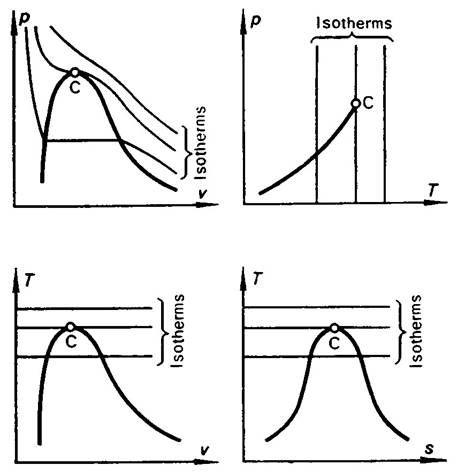
Fig. 7.5
As was shown in Chapter 1, the pressure and volume of an ideal gas are
related at any point on an isotherm by Boyle's law (1.17),
i.e. on
an isotherm plotted for an ideal gas the dependence of volume on pressure is
hyperbolic.
The isotherms of a real gas, liquids and solids are more-intricate (Fig.
7.5). It will be emphasized that for any substance, as was already mentioned in
Chapter 5, the quantity (dv/dp)T
cannot be positive and, consequently, along the isotherm a rise in
pressure is accompanied by a decrease in the specific volume of substance.
The work of expansion done by a system undergoing an isothermal process
proceeding between states 1 and 2 on an isotherm is determined
with the aid of the general relationship (3.1):
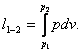
To calculate this integral, we must know the isothermal dependence of
pressure on the specific volume either from the equation of state or from
experimental data (in the latter case the integral is calculated applying
numerical methods).
Allowing for Eq. (1.23), for an ideal gas we obtain from Eq. (3.1):
(7.22)
The equation of an isotherm for an ideal gas can also be written in the
following form:
(7.22a)
The amount of heat added to a system (or rejected from the system)
undergoing an isothermal process is determined from the known relationship
Since T = const,
(7.23)
where s2 and s1 are the entropies in states 2 and 1, respectively. For an ideal gas, for
which, in accordance with Eq. (2.37),
the
mathematical statement of the first law of thermodynamics takes the following form:
(7.24)
It follows from this that in an isothermal process (dT = 0) for an ideal
gas
(7.25)
i.e.
the amount of work performed by an ideal gas undergoing an isothermal process
is equal to the amount of heat added to this gas:
(7.26)
where l12 is determined from
Eq. (7.22).
The change in entropy of a system undergoing an isothermal process, i.e.
the difference in the entropies corresponding to states 1 and 2, is calculated in the following way.
If the pressures at points 1 and 2 are known, then from
the relationship
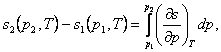(7.27)
making
use of Maxwell's relation (4.22), we obtain:
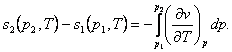(7.28)
But if the specific volumes at points 1 and 2 are known,
then from the relationship
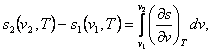(7.29)
allowing
for Maxwell's relation (4.23), we have:
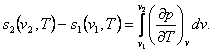(7.30)
To calculate the integrals present in the right-hand side of Eqs. (7.28)
and (7.30), we must know the values of (dv/dT)p
or (dp/dT)v
on the isotherm plotted for a given substance. These values can be
calculated either with the aid of the equations of state or by numerical or
graphical differentiation of the experimental data on the p-, v-,
T-dependencies for a given substance.
For an ideal gas, the integral present in Eq. (7.28) and (7.30) can be
easily calculated. Since for an ideal gas, as can be readily ascertained from Eq. (1.23),
(7.31)
and
(7.32)
we
obtain from Eqs. (7.28) and (7.30):
(7.33)
(7.34)
In conclusion, let us find the heat capacity inherent in an isothermal
process. From the definition of heat capacity it follows that if the addition
or removal of heat during an isothermal process does not lead to a change in
system temperature, the heat capacity cT is infinitely large:
(7.35)
(the
plus sign corresponds to addition of heat to a system, the minus sign indicates
the removal of heat from a system).