tests

Расчётные задачи
химической кинетики.

ЗАДАЧА 3.1, в которой при некоторой температуре Т по данным о константе скорости реакции определено изменение концентрации исходного вещества и скорости реакции в зависимости от времени в необратимой реакции первого порядка А ---------> B

ЗАДАЧА 3.2, в которой при некоторой температуре Т по данным о константе скорости реакции определено изменение концентрации исходного вещества и скорости реакции в зависимости от времени в необратимой реакции второго порядка 2А ---------> B

ЗАДАЧА 3.3, в которой по данным о константе скорости реакции
N 2 · O 5 --------> N 2 · O 4 + 1 2 O 2
при разичных температурах определена энергия активации реакции.

ЗАДАЧА 3.4, в которой исследуется влияние величины константы скорости k 1 на изменение концентраций веществ и скорости реакции в последовательной реакции первого порядка

À ---------> B ------------> C
k 1 k 2

Задача 3.5, в которой проверяется утверждение, что когда промежуточный продукт в последовательной реакции первого порядка

À ---------> B ------------> C
относительно мало устойчив, то есть когда константа его разложения k 2 в 10 раз превышает константу образования k 1 , то по истечении некоторого малого времени после начала реакции устанавливается приблизительно стационарная ( квазистационарная) концентрация промежуточного продукта, которая сохраняется значительную часть времени
течения реакции.

ЗАДАЧА 3.6, в которой по данным о зависимости времени полупревращения от начального давления аммиака, полученным при исследовании реакции разложения аммиака на вольфраме в качестве катализатора при различных температурах

2 NH 3 -------> N 2 + 3 H 2
определен порядок реакции, энергия активации и константы скорости реакции.

ЗАДАЧА 3.7, в которой по данным о зависимости начальной скорости реакции разложения тетрагидрофурана от его начального давления определен порядок реакции.

Задача 3.8, в которой исследуется зависимость концентрации веществ, участвующих в последовательной реакции первого порядка A ----> B ----> C ----> D от времени протекания процесса.

Задача 3.9, в которой исследуется зависимость скорости реакции по веществам, участвующим в последовательной реакции первого порядка A ----> B ----> C ----> D, от времени протекания процесса.

Задача 3.10, в которой исследуется зависимость концентрации веществ, участвующих в последовательно - параллельной реакции первого порядка

k 1 k 3
A --------> B ------------> D
A --------->C ------------> D
k 2 k 4

от времени протекания процесса.

Задача 3.11, в которой по экспериментальным данным о зависимости концентрации от времени в реакции разложения глюкозы в водном растворе определен порядок реакции, рассчитана константа скорости и зависимость степени превращения от времени.

Задача 3.12, в которой по данным о зависимости давления системы от времени определены порядок реакции и констана скорости реакции димерезации бутадиена при 599К.

Задача 3.13, в которой рассчитано изменение концентраций веществ со временем при протекании параллельных бимолекулярных реакций

k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .
Константы скорости k 1 и k 2 , а так же начальная концентрация NO заданы.

Задача 3.14, в которой для реакции

2NO + Cl2 ------> 2NOCl,

скорость которой описывается кинетическим уравнением третьего порядка, исследована зависимость крнцентрации реагирующих веществ от времени.

Задача 3.15, в которой определена зависимость концентраций от времени в последовательных реакциях второго порядка
2A ----> 2B -----> 2C
k 1 k 2

Задача 3.16, в которой исследуется возможность определения зависимости концентраци и и степени превращения c исходного вещества и продукта реакции от времени, а также зависимость времени достижения заданной концентрации (или степени превращения) от концентрации в реакциях вида

aA ---> bB,
если скорость реакции описывается кинетическим уравнением n - го порядка.

Задача 3.17, в которой исследуется возможеность определения зависимости концентрации и степени превращения c исходного вещества и продукта реакции от времени, а также зависимость времени достижения заданной концентрации (или степени превращения) от концентрации в обратимых реакциях вида
aA+bB <====> lL+mM,
если скорость реакции описывается кинетическим уравнением n - го порядка.

Задача 3.18, в которй исследуется зависимость концентрации исходных веществ и продуктов реакции от времени проведения процесса в обратимой реакции окисления оксида азота

2NO + O 2 <====> 2N O 2 ,
которая имеет третий порядок в прямом и второй порядок в обратном направлениях.

Задача 3.19, в которой для обратимой экзотермической реакции первого порядка
A <===>B
при различном времени протекания процесса определена температура Т, при которой степень превращения исходного вещества максимальна.

Задача 3.20, в которой сопоставляются предложенная схема реакции кинетическому уравнению, полученному в эксперименте при исследовании кинетики термического разложения ацетальдегида CH 3 · CHO при 673К.

Задача 3.1.
При некоторой температуре Т константа скорости реакции первого порядка

А ---------> B
равна 0.14 c - 1 .
Определите изменение концентрации вещества А и скорости реакции в зависимости от времени при этой температуре. Начальная концентрация вещества А c 0 = 0.1 моль/л.

Решение.
Кинетическое уравнение необратимой реакции первого порядка в дифференциальной форме имеет вид
r A = - &dd; &dd; ⁢ &tgr; ⁢ c ⁡ &tgr; = kc ⁡ &tgr; (1.1)
и после интегрирования при начальных условиях: при &tgr; =0 c ⁡ &tgr; = c 0

c ⁡ &tgr; = c 0 · e - k · &tgr; (1.2)
Тогда скорость реакции в зависимости от времени:

r A = kc 0 · e - k&tgr;
После подстановки значений начальной концентрации и константы скорости реакции концентрация вещества А в зависимости от времени ( в секундах) и скорость реакции (моль/ л с) :

Ввод параметров изменения времени, за которое исследуется концентрация исходного вещества и скорость реакции А ---------> B.
Время изменяется от 0 до 100с.

&tgr; &colon;=&Space; 0 , 5 .. 100

Ввод соотношения, определяющего зависимость концентрации исходного вещества от времени в реакции А ---------> B

c ⁡ &tgr; &colon;=&Space; 0.1 · e - 0.14 · &tgr;

Ввод соотношения, определяющего зависимость скорости реакции А ---------> B от времени протекания процесса.

r ⁡ &tgr; &colon;=&Space; 0.014 · e - 0.14 · &tgr;

Вывод результата - зависимость концентрации исходного вещества от времени в реакции А ---------> B

Вывод результата - зависимость скорости реакции А ---------> B от времени проведения процесса.

Рис. 1.1 и 1.2 иллюстрируют полученные результаты

Рис. 1.2. Зависимость скорости реакции
r( &tgr; ) от времени в необратимой реакции
первого порядка A ------> B.

Рис. 1.1. Зависимость концентрации c( &tgr; )
исходного вещества от времени в необратимой реакции первого порядка A ------> B.

Задача 3.2.
При некоторой температуре Т константа скорости реакции второго порядка

2 А ---------> B
равна 0.14 л/моль с.
Определите изменение концентрации вещества А и скорости реакции в зависимости от времени при этой температуре. Начальная концентрация вещества А c 0 = 0.1 моль/л.

Решение.
Кинетическое уравнение реакции второого порядка в дифференциальной
форме имеет вид
r A = - &dd; &dd; ⁢ &tgr; ⁢ c ⁡ &tgr; = kc ⁡ &tgr; 2 (2.1)
и после интегрирования при начальных условиях: при &tgr; =0 c ⁡ &tgr; = c 0

c ⁡ &tgr; = c 0 1 + kc 0 · &tgr; (2.2)
и скорость реакции в зависимости от времени:

r A = k · c 0 1 + kc 0 · &tgr; 2 (2.3)

После подстановки значений начальной концентрации и константы скорости реакци концентрация вещества А в зависимости от времени ( в секундах) и скорость реакции
(моль/ л с) :

&tgr; &colon;=&Space; 0 , 5 .. 100

c 0 &colon;=&Space; 0.1

k &colon;=&Space; 0.14

c 1 ⁡ &tgr; &colon;=&Space; c 0 1 + c 0 · k · &tgr;

Ввод соотношения, определяющего зависимость концентрации исходного вещества от времени в реакции второго порядка 2 А ---------> B

Ввод соотношения, определяющего зависимость скорости реакции второго порядка 2 А ---------> B от времени протекания процесса.

r 1 ⁡ &tgr; &colon;=&Space; k · c 0 1 + c 0 · k · &tgr; 2

Вывод результата - зависимость концентрации исходного вещества c 1 ⁡ &tgr; и скорости процесса r 1 ⁡ &tgr; в необратимой реакции второго порядка
2 А ---------> B
от времени протекания процесса.

Рис. 2.1 и 2.2 иллюстрируют полученные результаты

Рис. 2.1 Зависимость концентрации c 1 ⁡ &tgr;
исходного вещества от времени
в реакции второго порядка 2 А ---------> B

Рис. 2.2. Зависимость скорости реакции r 1 ⁡ &tgr; от времени в реакции второго порядка 2 А ---------> B

Сравнение временных зависимостей концентрации исходного вещества и скорости процессов для необратимых реакций первого и второго порядков (разумеется, при одинаковых начальных концентрациях и одинаковых числовых значениях констант скоростей ) приведено на рис. 2.3 и рис. 2.4.

Рис. 2.3. Сравнение временных зависимостей концентрации исходного вещества для необратимых реакций первого c ⁡ &tgr; и второго c 1 ⁡ &tgr; порядков.

Рис. 2.4. Сравнение временных зависимостей скорости процессов для необратимых реакций первого r ⁡ &tgr; и второго r 1 ⁡ &tgr; порядков.

Обратите внимание на ход временных зависимостей скорости процессов и концентраций исходного вещества для необратимых реакций первого и второго порядков..

Задача 3.3
Исследовали кинетику реакции
N 2 · O 5 --------> N 2 · O 4 + 1 2 O 2
при разичных температурах.
Были получены следующие значения констант скоростей ( c - 1 ) в зависимости от температуры:

T,K 556 575 629 647 666
k 3.52 · 10 - 7 1.22 · 10 - 6 3.02 · 10 - 5 8.59 · 10 - 5 2.19 · 10 - 4

Ò,Ê 683 700 716 784
k 5.12 · 10 - 4 1.16 · 10 - 3 2.5 · 10 - 3 3.95 · 10 - 2

Постройте графики зависимости константы скорости реакции k от температуры T и ln ⁡ k от 1 T .
Вычислите энергию активации этой реакции.

Решение.
Построим сначала график зависимости константы скорости реакции от температуры:

T &colon;=&Space; ( 556 575 629 647 666 683 700 716 784 )

k &colon;=&Space; ( 3.52 · 10 - 7 1.22 · 10 - 6 3.02 · 10 - 5 8.59 · 10 - 5 2.19 · 10 - 4 5.12 · 10 - 4 1.16 · 10 - 3 2.5 · 10 - 3 3.95 · 10 - 2 )

Рис. 3.1 Зависимость константы скорости реакции от температуры.

Константа скорости резко возрастает с увеличением температуры, поскольку зави-
симость описывается уравнением Аррениуса:

k = k 0 · e - E a RT , (3.1)
где k 0 и E a - соответственно предъэкспоненциальный множитель и энергия актива-
ции реакции.
После логарифмирования уравнения Аррениуса получим:

lnk = ln ⁡ k 0 - E a RT , (3.2 )

и в координатах lnk - 1 T зависимость линейна, что дает возможность рассчитать и
предъэкспоненциальный множитель и энергию активации.
Введем обозначение: Y.- вектор значений обратной температуры, lnk - вектор соот-
ветствующих значений константы скорости реакции.

ln ⁡ k &colon;=&Space; ( - 14.86 - 13.617 - 10.408 - 9.362 - 8.426 - 7.577 - 6.759 - 5.991 - 3.231 )

Y &colon;=&Space; ( 1.799 · 10 - 3 1.739 · 10 - 3 1.59 · 10 - 3 1.546 · 10 - 3 1.502 · 10 - 3 1.464 · 10 - 3 1.429 · 10 - 3 1.397 · 10 - 3 1.276 · 10 - 3 )

Рис. 3.2. Зависимость логарифма
константы скорости реакции

N 2 · O 5 ----------> N 2 · O 4 + 1 2 O 2
от обратной температуры.

Коэффициенты уравнения lnk = ln ⁡ k 0 - E a RT определим, используя метод наименьших квадратов.

x &colon;=&Space; ( 1.799 · 10 - 3 1.739 · 10 - 3 1.59 · 10 - 3 1.546 · 10 - 3 1.502 · 10 - 3 1.464 · 10 - 3 1.429 · 10 - 3 1.397 · 10 - 3 1.276 · 10 - 3 ) T

y &colon;=&Space; ( - 14.86 - 13.617 - 10.408 - 9.362 - 8.426 - 7.577 - 6.759 - 5.991 - 3.231 ) T

Здесь line ⁡ x y - вектор из двух элементов (a,b)
коэффициентов линейной регрессии a+bx.

line ⁡ x y = ( 25.022 - 2.223 · 10 4 )

Следовательно, уравнение lnk = ln ⁡ k 0 - E a RT ìîæíî записать:
lnk = 25.022 - 2.223 · 10 4 1 T
Теперь можно рассчитать предъэкспоненциальный множитель

k 0 &colon;=&Space; e 25.022 = 7.361 · 10 10
и энергию активации реакции

E &colon;=&Space; 2.223 · 10 4 · 8.31 = 1.853 · 10 5 Дж/моль

Тогда зависимость константы скорости реакции от температуры

k = 7.361 · 10 10 · e - 1.853 · 10 5 R · T

Сравнение экспериментальных значений константы скорости в зависимости
от температуры, приведеных в условии задачи, и значений, рассчитанных по полученному уравнению
k = 7.361 · 10 10 · e - 1.853 · 10 5 R · T ,
приведены на рис. 3.3.

f ⁡ t &colon;=&Space; line ⁡ x y 0 + line ⁡ x y 1 · t

Рис.3.3. Зависимость логарифма константы скорости реакции от обратной температуры. lnk - экспериментальные и f ⁡ t - расчетные данные.

Задача 3.4.
Исследуйте влияние величины константы скорости k 1 на изменение концентраций веществ и скорости реакции в последовательной реакции первого порядка

А ---------> B ------------> C (4.1)
k 1 k 2

Начальная концентрация вещества А равна 1 моль/ л., k 2 = 0.1 c - 1
Проанализируйте полученные зависимости.

Решение.

1. Зависимость изменения концентрации исходного вещества А и скорости реакции по веществу А от времени при изменении значения константы скорости k 1 от 0.1 до 1 c - 1 .
Зависимость концентрации исходного вещества от времени для реакции первого порядка описывается соотношением:

C ⁡ &tgr; = C 0 · e - k&tgr; (.4.2)

и тогда скорость реакции изменяется со временем:

r ⁡ &tgr; = k · C ⁡ &tgr; = kC 0 · e - k&tgr; (.4.3)

В листинге использованы обозначения: t - вектор значений времени,
C 1 ⁡ &tgr; -вектор значений концентраций исходного вещества А при значениях констант скорости реакций k 1 = 1; k 2 = 0.1; C 2 ⁡ &tgr; - вектор значений концентраций исходного вещества А при значениях констант скорости реакций k 1 = 0.5; k 2 = 0.1 и C 3 ⁡ &tgr; - вектор значений концентраций исходного вещества А при значениях констант скорости реакций k 1 = 0.2; k 2 = 0.1

Ввод времени, в течение которого
будет исследовано изменение концентрации - от нуля до ста секунд с шагом одна секунда..

&tgr; &colon;=&Space; 0 , 1 .. 100

c 0 &colon;=&Space; 1

Ввод значений констант скоростей k 1 и k 2 последовательной реакции первого порядка А ---------> B ------------> C

k 1 &colon;=&Space; 1

k 2 &colon;=&Space; 0.1

Ввод соотношения, определяющего зависимость концентрации исходного вещества от времени в последовательной реакции первого порядка А ---------> B ------------> C

C 1 ⁡ &tgr; &colon;=&Space; c 0 · e - k 1 · &tgr;

Вывод результата - зависимость концентрации исходного вещества от времени в последовательной реакции первого порядка А ---------> B ------------> C при значениях констант скоростей k 1 = 1; k 2 = 0.1

Рис. 4.1 Зависимость концентрации исходного вещества от времени в последовательной реакции первого порядка A ------> B -------> C. k 1 = 1; k 2 = 0.1

Проследим влияние на ход зависимости концентрация исходного вещества А - время - изменения константы скорости реакции до k 1 = 0.5 и k 2 = 0.1.

Ввод значения константы скорости k 1 последовательной реакции первого порядка А ---------> B ------------> C

k 1 &colon;=&Space; 0.5

C 2 ⁡ &tgr; &colon;=&Space; c 0 · e - k 1 · &tgr;

Рис.4.2 Изменение концентрации исходного вещества в зависимости от времени в последовательной реакции A ------> B -------> C
1: k 1 = 1; k 2 = 0.1, 2: k 1 = 0.5; k 2 = 0.1

k 1 &colon;=&Space; 0.2

C 3 ⁡ &tgr; &colon;=&Space; c 0 · e - k 1 · &tgr;

Рис. 4.3 Зависимость концентрации исходного вещества от времени в последовательной реакции первого порядка A ------> B -------> C при изменении значения константы скорости реакции.
1: k 1 = 1; k 2 = 0.1, 2: k 1 = 0.5; k 2 = 0.1; 3.: 1: k 1 = 0.2; k 2 = 0.1.

Полученный результат не трудно было предсказать исходя из анализа зависимости концентрации от времени для реакции первого порядка
C ⁡ &tgr; = c 0 · e - k 1 · &tgr;
Однако, численный результат может быть получен только в результате расчета.

2. Теперь рассмотрим влияние константы скорости реакции на изменение скорости процесса в зависимости от времени его проведения.
Анализ сооотношения
r ⁡ &tgr; = kC = kC 0 · e - k&tgr;

позволяет сделать качественный вывод: при уменьшении константы скорости реакции скорость процесса так же уменьшается, однако, чтобы получить количественные закономерности, необходим расчет.
В дальнейшем приняты следующие обозначения: r 1 ⁡ &tgr; - вектор значений скорости реакции A ---> B при константе скорости k 1 = 1, r 2 ⁡ &tgr; - вектор значений скорости реакции A ---> B при константе скорости k 1 = 0.5 и r 3 ⁡ &tgr; - вектор значений скорости реакции A ---> B при константе скорости k 1 = 0.2

Ввод значения константы скорости реакции и соотношения, определяющего зависимость скорости реакции A ---> B от времени в последовательной реакции первого порядка А ---------> B ------------> C

k 1 &colon;=&Space; 1

k 2 &colon;=&Space; 0.1

r 1 ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr;

Вывод результата - зависимость скорости реакции A --> B от времени в последовательной реакции первого порядка А ---------> B ------------> C при значениях констант скоростей k 1 = 1; k 2 = 0.1

Рис.4.4. Скорость реакции по исходному веществу в зависи-
мости от времени в последовательной реакции первого порядка A ------> B -------> C k 1 = 1; k 2 = 0.1

k 1 &colon;=&Space; 0.5

r 2 ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr;

Рис.4.5. Скорость реакции по исходному веществу в зависи-
мости от времени в последовательной реакции первого порядка
A ------> B -------> C. (Кривая 1: k 1 = 1; Кривая 2: k 1 = 0.5 )

k 1 &colon;=&Space; 0.2

r 3 ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr;

Рис. 4.6 Скорость реакции по исходному веществу в зависимости от
времени в последовательной реакции первого порядка A ------> B -------> C
при изменении величины константы скорости.

2. Теперь рассмотрим более сложный случай - влияние изменения константы скорости k 1 в последовательной реакции первого порядка
A ------> B -------> C

на зависимость концентрации промежуточного продукта В от времени.
Зависимость концентрации промежуточного продукта В от времени описывается соотношением:

c ⁡ &tgr; = k 1 · C 0 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1 (4.4)

В листинге использованы обозначения: t - вектор значений времени, c 1 ⁡ &tgr; -вектор значений концентраций промежуточного вещества B при значениях констант скорости реакций k 1 = 1; k 2 = 0.1; c 2 ⁡ &tgr; - вектор значений концентраций вещества B при значениях констант скорости реакций k 1 = 0.5; k 2 = 0.1 и c 3 ⁡ &tgr; - вектор значений концентраций промежуточного вещества B при значениях констант скорости реакций k 1 = 0.2; k 2 = 0.1

k 1 &colon;=&Space; 1

k 2 &colon;=&Space; 0.1

Ввод значений констант скоростей реакций и соотношения, определяющего зависимость концентрации промежуточного соединения от времени в последовательной реакции первого порядка А ---------> B ------------> C

c 1 ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Вывод результата - зависимость концентрации промежуточного соединения от времени в последовательной реакции первого порядка А ---------> B ------------> C
k 1 = 1; k 2 = 0.1

Рис. 4.7 Зависимость концентрации промежуточного вещества от времени в последовательной реакции первого порядка A ------> B -------> C.
k 1 = 1; k 2 = 0.1

k 1 &colon;=&Space; 0.5

k 2 &colon;=&Space; 0.1

c 2 ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Вывод результата - зависимость концентрации промежуточного соединения от времени в последовательной реакции первого порядка А ---------> B ------------> C
k 1 = 0.5; k 2 = 0.1

Рис. 4.8 Зависимость концентрации промежуточ-
ного вещества от времени в последовательной
реакции первого порядка A ------> B -------> C.
( Кривая 1: k 1 = 1; k 2 = 0.1; кривая 2: k 1 =0.5; k 2 = 0.1)

k 1 &colon;=&Space; 0.2

k 2 &colon;=&Space; 0.1

c 3 ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Вывод результата - зависимость концентрации промежуточного соединения от времени в последовательной реакции первого порядка А ---------> B ------------> C
k 1 = 0.2; k 2 = 0.1

Ðèñ.4.9. Çàâèñèìîñòü êîíöåíòðàöèè ïðîìåæóòî÷íî-
ãî ñîåäèíåíèÿ îò âðåìåíè â ïîñëåäîâàòåëüíîé ðåàêöèè
A ------> B ------>C ïðè ðàçëè÷íûõ çíà÷åíèõ êíñòàíòû ñêîðî-
ñòè ðåàêöèè. 1: k 1 = 1; k 2 = 0.1; 2: k 1 =0.5; k 2 = 0.1; 3. k 1 = =0.2; k 2 = 0.1.

Теперь рассмотрим частный, но достаточно интересный случай, когда константы скорости k 1 = k 2 = k .
При подстановке этого равенства в (4.4)

c ⁡ &tgr; = k 1 · C 0 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1
оно обращается в неопределенность.
Раскрыв неопределенность,

lim k 2 &rightarrow; k 1 C 0 · k 1 k 2 - k 1 · exp ⁡ - k 1 · &tgr; - exp ⁡ - k 2 · &tgr;

получим простую формулу для концентрации промежуточного соединения:

c 4 ⁡ &tgr; = C 0 · k&tgr;e - k&tgr; (4.5)

k &colon;=&Space; 0.1

c 0 &colon;=&Space; 1

c 4 ⁡ &tgr; &colon;=&Space; c 0 · k · &tgr; · e - k · &tgr;

Вывод результата - зависимость концентрации промежуточного соединения от времени в последовательной реакции первого порядка А ---------> B ------------> C
k 1 = 0.1; k 2 = 0.1

Рис. 4.10 Зависимость концентрации промежуточно-
го соединения от времени в последовательной реакции
A ------> B ------>C при значених кнстанты скоро-
сти реакции k 1 = k 2 = 0.1.

Теперь сравним ход зависимостей концентрации промежуточного соединения от времени в последовательной реакции A ------> B ------>C при различных значених кнстанты скорости реакции k 1 .

Рис. 4.11 Зависимость концентрации промежуточного соединения от времени в последовательной реакции A ------> B ------>C при различных значених кнстанты скорости реакции. c 4 ⁡ &tgr; : k 1 = 1; k 2 = 0.1; c 3 ⁡ &tgr; : k 1 =0.5; k 2 = 0.1; c 3 ⁡ &tgr; : k 1 =0.2; k 1 =0.1 c 4 ⁡ &tgr; : k 1 = k 2 = 0.1.

Как видно и из данных расчета и из рис. 4.11 зависимость концентрации промежуточного соединения от времени при всех значениях константы скорости реакции имеет максимум.
В этом можно было убедиться, проанализировав уравнение (4.4.):

c ⁡ &tgr; = k 1 · C 0 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1
При t ---> 0 и при t -----> ∞ функция c(t) стремится к нулю, но при промежуточных значениях времени концентрация промежуточного продукта отличается от нуля.
Время достижения максимального значения концентрации при отличающихся зна-
чениях констант скорости реакции k 1 и k 2 лего найти, продифференциировав ( 4.4.)

C ⁡ &tgr; = k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1
по времени

&dd; &dd; ⁢ &tgr; ⁢ C ⁡ &tgr; = k 1 · - k 1 · exp ⁡ - k 1 · &tgr; + k 2 · exp ⁡ - k 2 · &tgr; k 2 - k 1

и прировняв полученное выражение

k 1 · - k 1 · exp ⁡ - k 1 · &tgr; + k 2 · exp ⁡ - k 2 · &tgr; k 2 - k 1 = 0

к нулю.
Откуда
&tgr; max = ln ⁡ k 2 - ln ⁡ k 1 k 2 - k 1 (4.6)

И тогда ( при значении k 2 = 0.1):
&tgr; max · -CompileError ⁡ apply ⁡ -mkError "unmatched parenthesis" = 1) = 2.558c.
&tgr; max · -CompileError ⁡ apply ⁡ -mkError "unmatched parenthesis" =0.5) = 4.024c.
&tgr; max · -CompileError ⁡ apply ⁡ -mkError "unmatched parenthesis" =0.2) = 6.931c.

Подставив последнее выражение
&tgr; max = ln ⁡ k 2 - ln ⁡ k 1 k 2 - k 1
в (4.4):

C ⁡ &tgr; = k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1 ,

найдем значение максимальной концентрации:

C B , max = k 1 C 0 · k 2 k 1 - k 1 k 2 - k 1 - k 2 k 1 - k 2 k 2 - k 1 k 2 - k 1 (4.7)

Определим значение максимальной концентрации (моль/л) промежуточного соединения в зависимости от величины константы скорости реакции k 1 ( при значении k 2 =0.1):

k 2 &colon;=&Space; 0.1

Ввод соотношения, определяющего значение максимальной концентрации промежуточного соединения в последовательной реакции
A ------> B ------>C

C ⁡ k 1 &colon;=&Space; k 1 · k 2 k 1 - k 1 k 2 - k 1 - k 2 k 1 - k 2 k 2 - k 1 k 2 - k 1

C ⁡ 1 = 0.774

Вывод результата - значения максимальной концентрации промежуточного соединения последовательной реакции A ------> B ------>C при различных значениях константы скорости k 1

C ⁡ 0.5 = 0.669

C ⁡ 0.2 = 0.5

Аналогично определим время достижения максимальной концентрации промежуточного продукта при равенстве констант скоростей, продифференциировав соотношение (4.5 ):
c ⁡ &tgr; = C 0 · k · &tgr; · e - k · &tgr;
и прировняв полученное выражение к нулю
C 0 · k · exp ⁡ - k · &tgr; - C 0 · k 2 · &tgr; · exp ⁡ - k · &tgr; = 0
Получим уравнение, позволяющее рассчитать время достижения максимальной
концентрации промежуточного соединения при равенстве значений констант скоростей:
&tgr; max ⁡ k = 1 k
Например, при значениях констант скоростей k = 0.2:

&tgr; ⁡ k &colon;=&Space; 1 k

k &colon;=&Space; 0.2

&tgr; ⁡ k = 5

и максимальное значение концентрации промежуточного продукта в этом случае (после подстановки последнего соотношения
&tgr; ⁡ k = 1 k
в (4.5)):

c ⁡ &tgr; = C 0 · k · &tgr; · e - k · &tgr;

c max = � 0 · e - 1
зависит только от начальной концентрации.
Этот вывод иллюстрируется расчетами, приведенными в листинге и рис. 4.12 , где приняты обозначения: t - время, с., c ⁡ &tgr; , c 1 ⁡ &tgr; и c 2 ⁡ &tgr; - вектора значений концентраций промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы сорости реакции
k 1 = k 2 = k = 0.1;0.5;1 сответственно.

&tgr; &colon;=&Space; 0 , 1 .. 100

C 0 &colon;=&Space; 1

k &colon;=&Space; 0.1

c ⁡ &tgr; &colon;=&Space; C 0 · k · &tgr; · e - k · &tgr;

Вывод результата - зависимость
концентрации промежуточного соединения
от времени в последовательной реакции
первого порядка А ---------> B ------------> C
k 1 = 0.1; k 2 = 0.1

C 0 &colon;=&Space; 1

k &colon;=&Space; 0.5

c 1 ⁡ &tgr; &colon;=&Space; C 0 · k · &tgr; · e - k · &tgr;

Вывод результата - зависимость
концентрации промежуточного соединения
от времени в последовательной реакции
первого порядка А ---------> B ------------> C
k 1 = 0.5; k 2 = 0.5

C 0 &colon;=&Space; 1

k &colon;=&Space; 1

c 2 ⁡ &tgr; &colon;=&Space; C 0 · k · &tgr; · e - k · &tgr;

Вывод результата - зависимость концентрации промежуточного соединения от времени в
последовательной реакции первого порядка
А ---------> B ------------> C
k 1 = 1; k 2 = 1

Рис. 4.12 Зависимость концентрации промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы сорости реакции k 1 = k 2 = k;
1. k = 0.1; 2.k = 0.5; 3. k = 1

Представим, что промежуточное вещество В является тем целевым продуктом, ради получения которого проводят реакцию

A-------> B ------->C
k 1 k 2
Константы скорости k 1 и k 2 могут по разному зависеть от температуры, поскольку энергии активации реакций чаще всего различаются, а так же можно подобрать катализаторы, по разному ускоряющие ту и другую реакции.
Поэтому возникает естественный в такой ситуации вопрос: при каких температурах
проводить процесс, с целью максимального выхода целевого, в данном случае, промежу-
точного продукта.
С этой целью проведем анализ соотношения (4.7)

= k 1 C 0 · k 2 k 1 - k 1 k 2 - k 1 - k 2 k 1 - k 2 k 2 - k 1 k 2 - k 1

Исследуем это выражение при крайних значениях констант скорости.
1. Пусть k 1 >> k 2 и пусть, например, k 1 =10 и k 2 =0.1.
Рассмотрим изменение концентрации промежуточного соединения в этом случае:

k 1 &colon;=&Space; 10

k 2 &colon;=&Space; 0.1

C ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Вывод результата - зависимость концентрации промежуточного соединения от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 = 10; k 2 = 0.1

Рис. 4.13 Зависимость концентрации промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы скорости реакции k 1 = 10 и k 2 = 0.1

Анализ соотношения (4.4 )

C ⁡ &tgr; = k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1 ,

данные расчета C ⁡ &tgr; и их графическая интерпретация (рис.4.13) свидетельствуют о том, что при соблюдении условия k 1 >> k 2 промежуточный продукт относительно устойчив, и в этом случае значительная часть исходного вещества превращается в промежуточный продукт и накапливается в таком виде в течение некоторого времени.
И если промежуточное вещество - целевой продукт, то время контактирования в реакторе может быть определено.

Теперь рассмотрим случай, когда k 2 >> k 1 , то есть случай, когда промежуточный ïðîäóêò êðàéíå íåóñòîé÷èâ.

k 1 &colon;=&Space; 0.1

k 2 &colon;=&Space; 10

C 1 ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Рис. 4.14 Зависимость концентрации промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы скорости реакции k 1 = 0.1 и k 2 = 1

Как видно из расчетов и из рисунков (сравнение зависимостей концентрации промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы скорости реакции k 1 = 10 и k 2 = 0.1 и k 1 = 0.1 и k 2 = 1 приведено на рис.4.13, 4.14 и 4.15), максимальная концентрация промежуточного продукта в этом случае очень мала, а, значит, промежуточный ïðîäóêò êðàéíå íåóñòîé÷èâ. .

Рис. 4.15. Зависимость концентрации промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы скорости реакции 1. k 1 = 10 и k 2 = 0.1 2. k 1 = 0.1 и k 2 =1

Рассмотрим теперь зависимость концентрации конечного продукта последовательной реакции
A ----> B -------> C

от времени, которая описывается соотношением:

C(t) = C 0 · 1 + 1 · k 2 · e - k 1 · &tgr; - k 1 · e - k 2 · &tgr; k 1 - k 2
и одновременно проследим влияние значения константы скорости k 1 ( при постоянной k 2 =0.1) на ход этой зависимости.

&tgr; &colon;=&Space; 0 , 1 .. 100

C 0 &colon;=&Space; 1

k 1 &colon;=&Space; 1

k 2 &colon;=&Space; 0.1

Ввод значений начальной концентрации исходного вещества, констант скоростей реакций и соотношения, определяющего зависимость концентрации конечного продукта от времени в последовательной реакции первого порядка А ---------> B ------------> C.

c ⁡ &tgr; &colon;=&Space; C 0 · 1 + 1 · k 2 · e - k 1 · &tgr; - k 1 · e - k 2 · &tgr; k 1 - k 2

Вывод результата - зависимость концентрации промежуточного соединения от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 =1; k 2 = 0.1

Рис. 4.16 Зависимость концентрации конечного продукта С в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы скорости реакции k 1 =1 и k 2 = 0.1

C 0 &colon;=&Space; 1

k 1 &colon;=&Space; 0.5

k 2 &colon;=&Space; 0.1

c 1 ⁡ &tgr; &colon;=&Space; C 0 · 1 + 1 · k 2 · e - k 1 · &tgr; - k 1 · e - k 2 · &tgr; k 1 - k 2

Вывод результата - зависимость концентрации промежуточного соединения от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 =0.5; k 2 = 0.1

Рис. 4.17 Зависимость концентрации конечного продукта С в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы сорости реакции k 1 =0.5 и
k 2 = 0.1

Ввод значения константы скорости реакции и соотношения, определяющего зависимость концентрации конечного продукта от времени в последовательной реакции первого порядка А ---------> B ------------> C.

k 1 &colon;=&Space; 0.2

c 2 ⁡ &tgr; &colon;=&Space; C 0 · 1 + 1 · k 2 · e - k 1 · &tgr; - k 1 · e - k 2 · &tgr; k 1 - k 2

Вывод результата - зависимость концентрации промежуточного соединения от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 =0.2; k 2 = 0.1

Графическая иллюстрация полученных результатов приведена на рис. 4. 18.

Рис. 4.18 Зависимость концентрации конечного продукта С в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы сорости реакции k 2 = 0.1:1. k 1 =1; 2. k 1 =0.5; 3. k 1 = 0.2.

В заключение рассмотрим изменение концетраций веществ в последовательной
реакции первого порядка

A ------> B ------>C

при условии, что константа скорости k 2 > k 1 .
В листинге введены обозначения:
A ⁡ &tgr; - вектор значений концентрации исходного вещества A,
B ⁡ &tgr; - вектор значений концентрации промежуточного продукта B и
C ⁡ &tgr; - вектор значений концентрации конечного продукта C.

k 1 &colon;=&Space; 0.1

k 2 &colon;=&Space; 0.2

C 0 &colon;=&Space; 1

Ввод значений начальной концентрации исходного вещества, констант скоростей реакций и соотношения, определяющего зависимость концентрации исходного вещества от времени в последовательной реакции первого порядка А ---------> B ------------> C.

A ⁡ &tgr; &colon;=&Space; C 0 · e - k 1 · &tgr;

Вывод результата - зависимость концентрации исходного вещества от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 =0.1; k 2 = 0.1

B ⁡ &tgr; &colon;=&Space; k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Ввод соотношений, определяющих зависимость концентрации промежуточного соединения B(t) è конечного продукта C(t) от времени в последовательной реакции первого порядка А ---------> B ------------> C.

C ⁡ &tgr; &colon;=&Space; 1 + 1 · k 2 · e - k 1 · &tgr; - k 1 · e - k 2 · &tgr; k 1 - k 2

Вывод результата - зависимость концентрации промежуточного соединения B(t) è êîíå÷íîãî ïðîäóêòà C(t) от времени в последовательной реакции первого порядка
А ---------> B ------------> C k 1 =0.1; k 2 = 0.2

Рис. 4.18 Зависимость концентрации исходного вещества A (t), промежуточного соединения B (t) и конечного продукта С (t) в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях констант сорости реакции k 2 = 0.2 и k 1 =0.1.

Отметим особенность, характерную для зависимости концентрации конечного вещества от времени:
- функция C ⁡ &tgr; имеет точку перегиба,
- время, соответствующее этой точке, совпадает со временем достижения максимальной концентрации промежуточного продукта,поскольку вторая производная
&dd; 2 &dd; ⁢ &tgr; 2 ⁢ � ⁡ &tgr; =0 при &tgr; ��. = &tgr; max

Задача 3.5
Считается, что когда промежуточный продукт относительно мало устойчив, то есть когда константа его разложения k 2 в 10 раз превышает константу образования k 1 , уменьшение разности k 2 - k 1 ( при том же их отношении) приводит к растягиванию максимума во времени. Концентрация промежуточного продукта длительного времени остается приблизительно на одном низком уровне, близком к максимальному.
Это дает право считать, что по истечении некоторого малого времени после начала реакции устанавливается приблизительно стационарная (квазистационарная) концентрация промежуточного продукта, которая сохраняется значительную часть времени течения реакции.
Проверьте это утверждение.
Исследуйте изменение концентраций веществ в последовательной реакции первого порядка

À ---------> B ------------> C
k 1 k 2
при постоянном отношении
k 2 k 1 = 10

и следующих значениях констант скоростей: 1. k 1 = 0.1; k 2 = 1. 2. k 1 = 0.01; k 2 = 0.1. 3. k 1 =0.001; k 2 = 0.01.
Начальная концентрация вещества A равна 1 моль/л.

Решение.

Пусть

&tgr; &colon;=&Space; 0 , 10 .. 1000

C 0 &colon;=&Space; 1

Ввод значений начальной концентрации исходного вещества, констант скоростей реакций и соотношения, определяющего зависимость концентрации промежуточного соединения от времени в последовательной реакции первого порядка А ---------> B ------------> C.

k 1 &colon;=&Space; 0.1

k 2 &colon;=&Space; 1

c ⁡ &tgr; &colon;=&Space; k 1 · C 0 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Вывод результата - зависимость концентрации промежуточного соединения от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 =0.1; k 2 = 1

Рис. 5.1 Зависимость концентрации промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы сорости реакции k 1 = 0.1 и k 2 =1.

Рассмотрим второй случай:

2. k 1 &colon;=&Space; 0.01 ; k 2 :0.1

c 1 ⁡ &tgr; &colon;=&Space; k 1 · C 0 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Вывод результата - зависимость концентрации исходного вещества от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 =0.01; k 2 = 0.1

Рис. 5.2 Зависимость концентрации промежуточного соединения B в последовательной реакции
A ------> B ------>C
при начальной концентрации C 0 =1моль/л и значениях константы сорости реакции k 1 = 0.01 и k 2 =0.1.

И, наконец, рассмотрим ход зависимости концентрации промежуточного соединения от времени при значениях констант скорости реакции k 1 &colon;=&Space; 0.001 и k 2 &colon;=&Space; 0.01 .

&tgr; &colon;=&Space; 0 , 10 .. 1000

Ввод значений констант скоростей реакций и соотношения, определяющего зависимость концентрации исходного вещества от времени в последовательной реакции первого порядка А ---------> B ------------> C.

k 1 &colon;=&Space; 0.001

k 2 &colon;=&Space; 0.01

c 2 ⁡ &tgr; &colon;=&Space; k 1 · C 0 · e - k 1 · &tgr; - e - k 2 · &tgr; k 2 - k 1

Вывод результата - зависимость концентрации исходного вещества от времени в
последовательной реакции первого порядка
А ---------> B ------------> C k 1 =0.001; k 2 = 0.01

Рис. 5.2 Зависимость концентрации промежуточного
соединения от времени в последовательной реакции
A ------> B ------>C при различных значениях константы
скорости реакции. 1: k 1 = 0.1; k 2 = 1; 2: k 1 =0.01; k 2 = 0.1;
3. k 1 = 0.001; k 2 = 0.01.

Как видно из рис. 5.2, иллюстрирующего проведенные расчеты, о постоянстве, или даже о проблизительном постоянстве концентрации промежуточного соединения можно говорить с большим трудом только о ситуации (3), когда k 1 = 0.001 и k 2 = 0.01.
Проверим, насколько устанавливается приблизительно стационарная
( квазистационарная) концентрация промежуточного продукта в сравнении с изменением концентраций исходного вещества и конечного продукта в ходе реакции.

&tgr; &colon;=&Space; 0 , 10 .. 1500

Ввод значеий констант скоростей реакций и начальной концентрации исходного вещества.

k 1 &colon;=&Space; 0.001

k 2 &colon;=&Space; 0.01

c 0 &colon;=&Space; 1

Ввод соотношений, определяющих зависимость концентрации исходного вещества c 1 ⁡ &tgr; , промежуточного соединения c 2 ⁡ &tgr; и продукта c 3 ⁡ &tgr; последовательной реакции первого порядка А ---------> B ------------> C
от времени.

c 1 ⁡ &tgr; &colon;=&Space; c 0 · e - k 1 · &tgr;

c 2 ⁡ &tgr; &colon;=&Space; k 1 k 2 - k 1 · c 0 · e - k 1 · &tgr; - e - k 2 · &tgr;

c 3 ⁡ &tgr; &colon;=&Space; 1 k 2 - k 1 · c 0 · k 2 · 1 - e - k 1 · &tgr; - k 1 · 1 - e - k 1 · &tgr;

Вывод результата - зависимость концентрации исходного вещества c 1 ⁡ &tgr; , промежуточного соединения c 2 ⁡ &tgr; и продукта c 3 ⁡ &tgr; последовательной реакции первого порядка А ---------> B ------------> C от времени проведения процесса при значениях константы скорости реакции k 1 = 0.001; k 2 = 0.01..

Рис. 5.3. Зависимость концентрации исходного вещества c 1 ⁡ &tgr; промежуточного соединения c 2 ⁡ &tgr; и ко нечного продукта c 3 ⁡ &tgr; от времени в последовательной реакции
A ------> B ------>C
при значениях константы скорости реакции k 1 = 0.001; k 2 = 0.01.

По сравнению с резкими изменениями концентраций исходного вещества и конечного продукта концентрацию промежуточного вещества можно действительно считать квазистационарной.
Этот эффект соблюдается при достаточно малых значениях констант скоростей реакций и при условии, что k 2 > k 1 .

Задача 3.6.
При исследовании реакции разложения аммиака на вольфраме в качестве катализатора

2 NH 3 -------> N 2 + 3 H 2
при температурах 1173К и 1373К были получены следующие данные о времени полупревращения &tgr; 0.5 (в секундах) в зависимости от начального давления аммиака p 0 ( в паскалях). Продукты реакции в начальный момент отсутствуют.

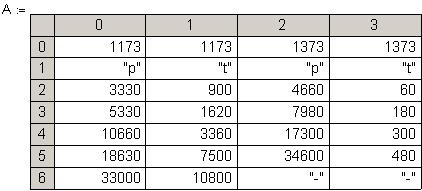
Определите порядок реакции по аммиаку n, энергию активации реакции E a , константы скорости реакции при исследованных температурах и изменение давления аммиака в зависимости от времени проведения процесса и температуры.

Решение.

Время полупревращения &tgr; 0.5 связано с порядком реакции n и начальной кон- центрацией C 0 следующим соотношением:

&tgr; 0.5 = C 0 1 - n 2 n - 1 - 1 k · n - 1 ( 6.1)

Или, поскольку концентрация газа прапорциональна его парциальному давлению:

&tgr; 0.5 = p 0 1 - n · 2 n - 1 - 1 k · n - 1 (6.2)

И после логарифмирования:

ln ⁡ &tgr; 0.5 = 1 - n · ln ⁡ C 0 + ln ⁡ 2 n - 1 - 1 k · n - 1 ( 6.3)

èëè äëÿ ãàçâûõ ðåàêöèé, êàê â ðàññìàòðèâàåìîì ñëó÷àå

ln ⁡ &tgr; 0.5 = 1 - n · ln ⁡ p 0 + ln ⁡ 2 n - 1 - 1 k · n - 1 (6.4)

Графически зависимость ( 6.3) или (6.4) представляет собой прямую с тангенсом угла наклона, равным (1 - n), что дает возможность определить порядок реакции.
Метод особенно полезен при дробном порядке реакции.
Однако построим прежде всего график зависимости времени полупревращения &tgr; 0.5 от начального давления p.
Приняты обозначения: p - вектор значений начального давления, &tgr; 0.5 - вектор соответствующих значений времени полупревращения, z - вектор значений z = ln ⁡ &tgr; 0 5

p 0 &colon;=&Space; ( 3.33 · 10 3 5.33 · 10 3 10.66 · 10 3 18.63 · 10 3 33.0 · 10 3 )

&tgr; 0 5 &colon;=&Space; ( 0.9 · 10 3 1.62 · 10 3 3.36 · 10 3 7.50 · 10 3 10.8 · 10 3 )

Рис. 6.1 График зависимости времени полупревращения от начального давления при Т= 1173К

С учетом неизбежного экспериментального разброса данных, зависимость близка к линейной, что возможно, как следует из (6.2)

&tgr; 0.5 = p 0 1 - n · 2 n - 1 - 1 k · n - 1

только в том случае, когда порядок реакции n = 0.
Для проверки этого утверждения исследуем зависимость логарифма времени полупревращения от логарифма начального давления при Т= 1173К â ðåàêöèè ðàçëîæåíèÿ àììèàêà в соответствии с (6.4):

ln ⁡ &tgr; 0.5 = 1 - n · ln ⁡ p 0 + ln ⁡ 2 n - 1 - 1 k · n - 1 .

log ⁡ p 0 = ( 3.522 3.727 4.028 4.27 4.519 )

log ⁡ &tgr; 0 5 = ( 2.954 3.21 3.526 3.875 4.033 )

Рис. 6.2 Зависимость логарифма времени полупревращения от логарифма начального давления при Т= 1173К â ðåàêöèè ðàçëîæåíèÿ àììèàêà.

Минимизировать совокупность возможных экспериментальных ошибок позволяет мате- матическая регрессия, задачей которой является приближение в некотором смысле выборки данных x i , y i некоторой функцией f(x), минимизирующей совокупность ошибок | f ⁡ x i - y i | .
Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость f(x).
Поскольку было сделано предположение о линейной зависимости времени полупревращения от начального давления, воспользуемся линейной регрессией: MathCAD представляет такую возможность.
В этом случае приближение данных x i , y i осуществляется линейной функцией вида y = b+ax с помощью встроенной функции line(x,y).

log ⁡ p 0 &colon;=&Space; ( 3.522 3.727 4.028 4.27 4.519 ) T

Ввод транспонированных матриц
значений логарифма начального давления р и логарифма времени полупревращения t

log ⁡ &tgr; 0 5 &colon;=&Space; ( 2.954 3.21 3.526 3.875 4.033 ) T

Вывод результата.

line ⁡ log ⁡ p 0 log ⁡ &tgr; 0 5 = ( 0 1 )

коэффициент b линейной регрессии
log ⁡ &tgr; 0 5 = b + a · log ⁡ p 0

intercept ⁡ log ⁡ p 0 log ⁡ &tgr; 0 5 = 0

коэффициент a линейной регрессии
log ⁡ &tgr; 0 5 = b + a · log ⁡ p 0

slope ⁡ log ⁡ p 0 log ⁡ &tgr; 0 5 = 1

Равенство коэффициента a линейной регрессии единице в соответствии с (6.4)

ln ⁡ &tgr; 0.5 = 1 - n · ln ⁡ p 0 + ln ⁡ 2 n - 1 - 1 k · n - 1

возможно только тогда, когда порядок реакции n=0.

Тогда
&tgr; 0.5 = p 0 · 1 2 · k , (6.5)

откуда константа скорости реакции:

k = 1 2 · &tgr; 0 5 · p 0 (6.6)

Последнее соотношение дает возможность определить константу скорости, если известны начальные давления аммиака p 0 и соответствующие значения времени полупревращения &tgr; 0 5 :

Ввод начального давления аммиака и соответствующего времени полупревращения при 1173К.

p 0 &colon;=&Space; ( 3.33 · 10 3 5.33 · 10 3 10.66 · 10 3 18.63 · 10 3 33.0 · 10 3 )

&tgr; 0 5 &colon;=&Space; ( 0.9 · 10 3 1.62 · 10 3 3.36 · 10 3 7.50 · 10 3 10.8 · 10 3 )

Ввод соотношения, связывающего константу скорости с начальным давлением и соответствующим временем полупревращения для реакции нулевого порядка.

k ⁡ p 0 &tgr; 0 5 &colon;=&Space; 1 2 · &tgr; 0 5 · p 0

k ⁡ 3.33 · 10 3 0.9 · 10 3 = 1.85

Вывод результата - значения константы скорости при 1173К и различных значениях начального давления и соответствующего времени полупревращения.
Разброс значений не носит систематического характера, поэтому будем считать его причиной экспериментальные погрешности при определении начального давления и времени полупревращения.
Определим среднее значение константы скорости при 1173К

k ⁡ 5.33 · 10 3 1.62 · 10 3 = 1.645

k ⁡ 10.66 · 10 3 3.36 · 10 3 = 1.586

k ⁡ 18.63 · 10 3 7.50 · 10 3 = 1.242

k ⁡ 33.0 · 10 3 10.8 · 10 3 = 1.528

Ввод соотношения, определяющего среднее значение константы скорости.

k �� &colon;=&Space; k ⁡ p 0 &tgr; 0 5 5

Вывод результата - среднее значение константы скорости реакции разложения аммиака при 1173К

k �� = 1.57

Теперь можно рассчитать время полупрвращения в реакции разложения аммиака при 1173К, используя среднее значение константы скорости реакции, и сравнить расчетные значения с экспериментальными, приведенными в условии задачи.

Ввод соотношения, определяющего время полупревращения в реакции нулевого порядка.

t 0 5 ⁡ p 0 &colon;=&Space; p 0 · 1 2 · k ��

Вывод результата - время полупревращения в реакции разложения аммиака при 1173К, рассчитанное на основании среднего значения константы скорости реакции.

t 0 5 ⁡ p 0 = ( 1.06 · 10 3 1.697 · 10 3 3.394 · 10 3 5.932 · 10 3 1.051 · 10 4 )

Экспериментальные ( &tgr; 0 5 ) значения времени полупревращения в реакции разложения аммиака на вольфраме
2 NH 3 -------> N 2 + 3 H 2
в зависимости от начального давления p 0 аммиака при 1173К. (Äàííûå óñëîâèÿ çàäà÷è.)

p 0 &colon;=&Space; ( 3.33 · 10 3 5.33 · 10 3 10.66 · 10 3 18.63 · 10 3 33.0 · 10 3 )

&tgr; 0 5 ⁡ p 0 &colon;=&Space; ( 0.9 · 10 3 1.62 · 10 3 3.36 · 10 3 7.50 · 10 3 10.8 · 10 3 )

Рис. 6. 3. Экспериментальные ( &tgr; 0 5 ) и расчетные ( t 0 5 ) значения времени полупревращения в реакции разложения аммиака на вольфраме

2 NH 3 -------> N 2 + 3 H 2
в зависимости от начального давления p 0 аммиака при 1173К.

Проведем теперь те же процедуры для определения константы скорости при температуре Т= 1373К, считая, что при увеличении температуры механизм реакции не изменяется и реакция разложения аммиака на вольфраме при этой температуре протекает как реакция нулевого порядка.

Ввод матриц значений начального давления р и времени полупревращения t ïðè 1373Ê

p 0 &colon;=&Space; ( 4.66 · 10 3 7.98 · 10 3 17.3 · 10 3 34.6 · 10 3 )

&tgr; 0 5 &colon;=&Space; ( 0.06 · 10 3 0.18 · 10 3 0.30 · 10 3 0.48 · 10 3 )

k ⁡ p 0 &tgr; 0 5 &colon;=&Space; 1 2 · &tgr; 0 5 · p 0

k ⁡ 4.66 · 10 3 0.06 · 10 3 = 38.833

Вывод результата - значения константы скорости при 1373К и различных значениях начального давления и соответствующего времени полупревращения.
Разброс значений не носит систематического характера, поэтому будем считать его причиной экспериментальные погрешности при определении начального давления и времени полупревращения.
Определим среднее значение константы скорости при 1373К

k ⁡ 7.98 · 10 3 0.18 · 10 3 = 22.167

k ⁡ 17.3 · 10 3 0.30 · 10 3 = 28.833

k ⁡ 34.6 · 10 3 0.48 · 10 3 = 36.042

Ввод соотношения, определяющего среднее значение константы скорости.

k �� &colon;=&Space; k ⁡ p 0 &tgr; 0 5 4

Вывод результата - среднее значение константы скорости реакции разложения аммиака при 1373К

k �� = 31.469

Ввод соотношения, определяющего время полупревращения в реакции нулевого порядка.

t 0 5 ⁡ p 0 &colon;=&Space; p 0 · 1 2 · k ��

Вывод результата - время полупревращения в реакции разложения аммиака при 1373К, рассчитанное на основании среднего значения константы скорости реакции.

t 0 5 ⁡ p 0 = ( 74.042 126.792 274.876 549.752 )

Ввод значений начального давления аммиака p 0 , экспериментальных значений времени полупревращения &tgr; 0 5 и рассчитанных по уравнению регоессии (6.4) t 0 5 при 1373К.

p 0 &colon;=&Space; ( 4.66 · 10 3 7.98 · 10 3 17.3 · 10 3 34.6 · 10 3 )

&tgr; 0 5 &colon;=&Space; ( 0.06 · 10 3 0.18 · 10 3 0.30 · 10 3 0.48 · 10 3 )

t 0 5 &colon;=&Space; ( 74.042 126.792 274.876 549.752 )

Рис. 6.4 Сравнение экспериментальных &tgr; 0 5 и полученных в результате регрессии t 0 5 данных по времени полупревращения при Т=1373К

Для определения энергии активации Е реакции используем уравнение
Аррениуса
k = k 0 · e - E RT

Или в логарифмическом виде:
lnk = ln k 0 - E R 1 T

Очевидно, что логарифм константы скорости есть линейная функция от обратной температуры.
Введем обозначения:
j - вектор значений обратной температуры,
l - вектор значений логарифма константы скорости реакции при соответствующих температурах и найдем коэффициенты ln k 0 и E R уравнения линейной регрессии, связываящего логарифм константы скорости и обратную температуру.

Ввод транспонированных матриц
значений обратной температуры j
и натурального логарифма константы скорости реакции l при соответствующих температурах.

j &colon;=&Space; ( 8.525 · 10 - 4 7.855 · 10 - 4 7.283 · 10 - 4 ) T

l &colon;=&Space; ( 0.451 2.229 3.449 ) T

Здесь line(j,l) - вектор из двух элементов
коэффициентов линейной регрессии.

line ⁡ j l = ( 21.136 - 2.421 · 10 4 )

f ⁡ t &colon;=&Space; line ⁡ j l 0 + line ⁡ j l 1 · t

Таким образом, зависимость логарифма константы скорости от температуры можно описать соотношением:

ln ⁡ k = 21.136 - 2.421 · 10 4 · 1 T (6.7)

и энергия активации E a исследуемой реакции равна

E a = 2.421 · 10 4 · 8.31 = 2.012 · 10 5 Дж/моль,

а предъэкспоненциальный множитель

k 0 = e 21.136 = 1.511 · 10 9

Тогда уравнение Aррениуса в логарифмическом виде можно записать:

lnk = 21.136 - 201200 RT
или
k = 1.511 · 10 9 · e - 201200 R · T , (6.8)

что дает возможность рассчитать константу скорости при любой температуре, а, следовательно, и скорость реакции при этой температуре ( ведь кинетическое уравнение нам известно), а так же изменение концентрации ( парциального давления аммиака) в зависимости от времени проведения процесса.
Рассчитаем значения констант скоростей реакции по уравнению ( 6.8):

R &colon;=&Space; 8.31

k 1 ⁡ T &colon;=&Space; 1.511 · 10 9 · e - 201200 R · T

При температуре Т = 1173К

k 1 ⁡ 1173 = 1.641

При температуре Т = 1273К

k 1 ⁡ 1273 = 8.303

При температуре Т = 1373К

k 1 ⁡ 1373 = 33.175

Для построения графика необходимо привести :
t - вектор значений обратной температуры,
lk - вектор значений логарифма констант скоростей реакции при соответствующих температурах, рассчитанных по экспериментальным данным ( уравнение 6.6)

k = 1 2 · &tgr; 0 5 · p 0

lk 1 - вектор значений логарифма констант скоростей реакции при соответствующих температурах, рассчитанных по уравнению регрессии ( уравнение 6.8)

t &colon;=&Space; ( 8.526 · 10 - 4 7.855 · 10 - 4 7.283 · 10 - 4 )

lk &colon;=&Space; ( 0.451 2.229 3.449 )

lk 1 &colon;=&Space; ( 0.495 2.117 3.502 )

Рис. 6.5 Влияние температуры на логарифм константы скорости реакции разложения аммиака.
lk 1 - расчетные данные, lk - экспериментальные данные.

Рассмотрим теперь влияние температуры на изменение парциального давления аммиака в зависимости от времени проведения процесса.

Поскольку реакция подчиняется кинетическому уравнению нулевого порядка, то зависисимость парциального давления аммиака p от времени проведения процесса (интегральная форма кинетического уравнения) с учетом влияния температуры на константу скорости может быть описана соотношением:

p ⁡ P 0 T &tgr; = P 0 - k · e E a R · T · &tgr;

, ãäå P 0 - íà÷àëüíîå äàâëåíèå àììèàêà ïðè &tgr; = 0

p ⁡ &tgr; T P 0 &colon;=&Space; P 0 - 1.511 · 10 9 · e - 201200 8.31 · T · &tgr;

Рассчитаем изменение давления аммиака p ( в Па) в зависимости от времени t ( время в секундах) при начальном давлении P 0 = 3.33 · 10 3 Па и температурах 900K ( p 1 ), 1173К ( p 2 ) и 1200К ( p 3 )

p ⁡ 100 1173 3.33 · 10 3 = 3.166 · 10 3

Вывод результата - давление аммиака в реакции его разложения на вольфраме в зависимости от времени проведения процесса t при 1173К и начальном давлении
P 0 = 3.33 · 10 3 Па.

Àíàëîãè÷íûì îáðàçîì ïîëó÷åíû ðåçóëüòàòû ïðè òåìïåðàòóðàõ 900Ê ( p 1 ) è 1200Ê. ( p 3 ).

p ⁡ 500 1173 3.33 · 10 3 = 2.51 · 10 3

p ⁡ 900 1173 3.33 · 10 3 = 1.853 · 10 3

p ⁡ 1000 1173 3.33 · 10 3 = 1.689 · 10 3

p ⁡ 1500 1173 3.33 · 10 3 = 868.951

p ⁡ 1750 1173 3.33 · 10 3 = 458.776

&tgr; &colon;=&Space; ( 0 100 500 900 1000 1500 1750 )

p 3 &colon;=&Space; ( 3.33 · 10 3 3.043 · 10 3 1.896 · 10 3 749.549 462.832 )

p 1 &colon;=&Space; ( 3.33 · 10 3 3.327 · 10 3 3.313 · 10 3 3.299 · 10 3 3.296 · 10 3 3.278 · 10 3 3.27 · 10 3 )

p 2 &colon;=&Space; ( 3.33 · 10 3 3.158 · 10 3 2.468 · 10 3 1.779 · 10 3 1.607 · 10 3 745.036 314.209 )

Результаты представлены и на рисунке 6.4

Рис. 6.4. Влияние температуры на изменение парциального давления аммиака.
p 1 . T= 900K, p 2 . T= 1173K, p 3 . T= 1200K

Задача 3.7 .

При проведении реакции разложения тетрагидрофурана при 550К были получены следующие данные о зависимости начальной скорости реакции r 0 от начального давления тетрагидрофурана p 0 :

p 0 · 10 - 3 , Па r 0 , �� · � - 1
10.56 4.43
13,33 5.97
17.20 8.43
21.10 11.60
26.60 17.66
33.4 0 23.80
42.10 35.20

Определите порядок реакции по тетрагидрофурану.

Решение.

Скорость реакции в начальный момент и начальное давление связаны соотношением
r 0 = &dd; &dd; ⁢ &tgr; ⁢ p = k · p 0 n , где k - константа скорости реакции и n - порядок реации.
После логарифмиравания:

ln ⁡ &dd; &dd; ⁢ &tgr; ⁢ p = ln ⁡ k + n · ln ⁡ p 0

Значения ln ⁡ &dd; &dd; ⁢ &tgr; ⁢ p и ln ⁡ p 0 приведены в таблице:
ln ⁡ p 0 ln ⁡ &dd; &dd; ⁢ &tgr; ⁢ p

9.265 1.488
9.498 1.787
9.753 2.132
9.957 2.451
10.189 2.871
10.416 3.17
10.648 3.561

Введем обозначения (для удобства построения графика):

ln ⁡ p 0 =lp è ln ⁡ &dd; &dd; ⁢ &tgr; ⁢ p = lr

Ввод значений логарифма начального давления lp и логарифма скорости реакции lr при соответствующем начальном давлении.

lp &colon;=&Space; ( 9.265 9.498 9.753 9.957 10.189 10.416 10.648 )

lr &colon;=&Space; ( 1.488 1.787 2.132 2.451 2.871 3.17 3.651 )

На рис. 7.1 показан график исследуемой зависимости.

Ðèñ. 7.1 Çàâèñèìîñòü ëîãàðèôìà íà÷àëüíîé ñêîðîñòè ðåàêöèè ðàçëîæåíèÿ òåòðàãèäðîôóðàíà îò íà÷àëüíîãî äàâëåíèÿ.

Зависимость в пределах исследуемых начальных давлений хорошо укладывается на прямую, поэтому для определения коэффициентов уравнения ln ⁡ &dd; &dd; ⁢ &tgr; ⁢ p = ln ⁡ k + n · ln ⁡ p 0 можно воспользоваться линейной регрессией, для расчета которой в MathCAD имеются два способа.
Воспользуемся линейной регрессией.

lp &colon;=&Space; ( 9.265 9.498 9.753 9.957 10.189 10.416 10.648 ) T

Ввод транспонрованных матриц значений логарифмов начального давления lp и логарифмов начальной скорости реакции lr .

lr &colon;=&Space; ( 1.488 1.787 2.132 2.451 2.871 3.17 3.651 ) T

Вывод результата - значения коэффициентов a и b уравнения линейной регрессии lr = a + b · lp

line ⁡ lp lr = ( - 12.987 1.556 )

Тогда:

Ввод уравнения регрессии - зависимость логарифма начальной скорости от логарифма начального давления реакции разложения тетрагидрофурана при 550К.

lR ⁡ lp &colon;=&Space; - 12.987 + 1.556 · lp

Вывод результата - расчетная зависимость логарифма начальной скорости.

lR ⁡ lp &colon;=&Space; ( 1.415 1.792 2.189 2.506 2.867 3.22 3.581 )

Сравним экспериментальные lr и ïîñòðîåííûå ïî äàííûì ëèíåéíîé ðåãðåññèèè lR(lp) зàâèñèìîñòè ëîãàðèôìà íà÷àëüíîé ñêîðîñòè ðåàêöèè ðàçëîæåíèÿ òåòðàãèäðîôóðàíà îò íà÷àëüíîãî äàâëåíèÿ.
Ðåçóëüòàòû ïðåäñòàâëåíû íà ðèñ. 7.2.

lp &colon;=&Space; ( 9.265 9.498 9.753 9.957 10.189 10.416 10.648 )

lr &colon;=&Space; ( 1.488 1.787 2.132 2.451 2.871 3.17 3.651 )

Ðèñ. 7.2 Çàâèñèìîñòü ëîãàðèôìà íà÷àëüíîé ñêîðîñòè ðåàêöèè ðàçëîæåíèÿ òåòðàãèäðîôóðàíà îò íà÷àëüíîãî äàâëåíèÿ : lr- ýêñïåðèìåíòàëüíûå ðåçóëüòàòû, lR(lp) - ïîñòðîåíî ïî äàííûì ðàñ÷åòà ëèíåéíîé ðåãðåññèèè.

Расчет линейной регрессии дает значение порядка реакции n= 1.56 и константы скорости к= e - 12.987 = 2.29 · 10 - 6 .
Рассчитаем значение начальной скорости реакции, используя найденное значение порядка, и сравним с экспериментальными результатами.

Ввод соотношения, определяющего скорость исследуемой реакции в зависимости от начального давления.

r ⁡ p &colon;=&Space; 2.29 · 10 - 6 · p 1.556

Результат счета - вывод результата: скорость реакции r ⁡ p при давлении 42100 Па.

r ⁡ 42100 = 35.91

Ввод значений начального давления p , экспериментальных r 0 (представленных в условии задачи) и расчетных (по полученному кинетическому уравнению r ⁡ p = 2.29 · 10 - 6 · p 1.556 ) значений начальной скорости

p &colon;=&Space; ( 10560 13330 17200 21100 26600 33400 42100 )

r 0 &colon;=&Space; ( 4.43 5.97 8.43 11.60 17.66 23.80 35.20 )

r ⁡ p &colon;=&Space; ( 4.175 6.00 8.919 12.258 17.577 25.049 35.910 )

Рис. 7.3. Сравнение экспериментальных r 0 и расчетных -CompileError ⁡ apply ⁡ -mkError "unmatched parenthesis" ) значений начальной скорости реакции разложения тетрагидрофурана при 550К в зависимости от начального давления..

Таким образом, скорость реакции разложения тетрагидрофурана при 550К можно описать кинетическим уравнением

r ⁡ p = 2.29 · 10 - 6 · p 1.556 , (7.1)
что дает возможность проследить, как изменяется давление тетрагидрофурана во времени.
Для этого решим дифференциальное уравнение (7.1), используя блок
Given/ Odesolve/

Ввод предъэкспоненты и порядка реакциии.

k 0 &colon;=&Space; 2.29 · 10 - 6

n &colon;=&Space; 1.556

Ввод ключевого слова

Given

Ââîä äèôôåðåíöèàëüíîãî óðàâíåíèÿ, îïðåäåëÿþùåãî êèíåòèêó èññëåäóåìîãî ïðîöåññà.

&dd; &dd; ⁢ &tgr; ⁢ p ⁡ &tgr; = - k 0 · p ⁡ &tgr; n

Ввод начального давления тетрагидрофурана

p ⁡ 0 = 10560

p &colon;=&Space; Odesolve ⁡ &tgr; 15000

p = function

Ввод времени. Зависимость давления тетрагидрофурана исследуется в течение 15000 секунд с интервалом 50с.

&tgr; &colon;=&Space; 0 , 50 .. 15000

Вывод результата - зависимость давления тетрагидрофурана от времени проведения процесса при 550К..

Графическая иллюстрация результатов приведена на рис. 7.4.

Рис.7.4. Зависимость давления тетрагидрофурана от времени проведения процесса при 550К..

Задача 3.8.
По известным значениям констант скоростей отдельных стадий превращения циклической трифосфорной кислоты в монофосфорную рассчитайте текущие концентрации всех участников реакции - циклической трифосфорной кислоты (A ), трифосфорной цепочечной (B), дифосфорной (C) и монофосфорной (D) при 333К.

A ---->B ------->C ----->D

k 1 k 2 k 3
k 1 = 5.4 1/ч ; k 2 = 0.6 1/ч; k 3 = 0.2 1/ч

Решение.
Кинетические уравнения:

по веществу A
r A = &dd; &dd; ⁢ &tgr; ⁢ C A = - k 1 · C A (8.1)

по веществу B
r B = &dd; &dd; ⁢ &tgr; ⁢ C B = k 1 · C A - k 2 · C B (8.2)
по веществу C
r C = &dd; &dd; ⁢ &tgr; ⁢ C C = k 2 · C B - k 3 · C C (8.3)

и по вешеству D
r D = &dd; &dd; ⁢ &tgr; ⁢ C D = k 3 · C C (8.4)

Задача сводится к решению системы дифференциальных уравнений (8.1 - 8.4):

&dd; &dd; ⁢ &tgr; ⁢ C A = - k 1 · C A
&dd; &dd; ⁢ &tgr; ⁢ C B = k 1 · C A - k 2 · C B

&dd; &dd; ⁢ &tgr; ⁢ C C = k 2 · C B - k 3 · C C

&dd; &dd; ⁢ &tgr; ⁢ C D = k 3 · C C
Для решения воспользуемся имеющейся в математическом пакете MathCAD встроенной функции rkfixed , позволяющей решать поставленную задачу методом Рунге - Кутты с встроенным шагом.
Введем обозначения: C 0 - текущая концентрация вещества A, C 1 - концентрация вещества B, C 2 - концентрация вещества C, C0 - вектор начальных значений концентраций при t = 0.

Ввод системы дифференциальных уравнений.

D ⁡ &tgr; C &colon;=&Space; ( - 5.4 · C 0 5.4 · C 0 - 0.6 · C 1 0.6 · C 1 - 0.2 · C 2 0.2 · C 2 )

Ввод начальных условий.

C0 &colon;=&Space; ( 1 0 0 0 )

Ввод числа шагов, на которых численный метод находит решение.

M &colon;=&Space; 100

Ввод встроенной функции rkfixed ⁡ C0 &tgr;0 &tgr;1 M D , где C0 - вектор начальных значений, &tgr;0 - начальная точка расчета, &tgr;1 - конечная точка расчета, M - число шагов, на которых численный метод находит решение.

u &colon;=&Space; rkfixed ⁡ C0 0 10 M D

Вывод решения в виде матрицы u.
В левом столбце матрицы находятся значения аргумента t, äåëÿùèå èíòåðâàë âðåìåíè íà ðàâíîìåðíûå øàãè, â îñòàëüíûõ ñòîëáöàõ - çíà÷åíèÿ èñêîìûõ çàâèñèìîñòåé êîíöåíòðàöèé âåùåñòâ îò âðåìåíè: C A · &tgr; , C B · &tgr; , C C · &tgr; , C D · &tgr; .
Íà ðèñ. 8.1 ïðèâåäåíà ãðàôè÷åñêàÿ èëëþñòðàöèÿ ïîëó÷åííûõ ðåçóëüòàòîâ.

Рис. 8.1. Текущие концентрации превращения циклической трифосфорной кислоты в ммонофосфорную - циклическая трифосфорная кислота (A - ( u < 1 > )), трифосфорная цепочечная (B - ( u < 2 > )), дифосфорная (C - ( u < 3 > )) и монофосфорная (D - ( u < 4 > )) при 333К.
A ---->B ------->C ----->D

Задача 3.9.
Исследуйте зависимость скорости реакций по веществу A, B, C и D
в зависимости от времени протекания процесса в последовательной реакции
первого порядка

A----> B ----> C -----> D,

k 1 k 2 k 3
если при 333К и pH = 0 константы скорости реакций соответственно
равны: k 1 = 0.44 1/ч; k 2 = 0.2 1/ч; k 3 = 0.1 1/ч. Начальная концентрация
вещества А C 0 &colon;=&Space; 1.0 моль/л

Решение.
Напрашивается следующее очевидное решение задачи:
зависать кинетические уравнения реакций

по веществу A
r A ⁡ &tgr; = - &dd; &dd; ⁢ &tgr; ⁢ C A ⁡ &tgr; = k 1 · C A ⁡ &tgr; (9.1)
по веществу B

r B ⁡ &tgr; = &dd; &dd; ⁢ &tgr; ⁢ C B ⁡ &tgr; = k 1 · C A ⁡ &tgr; - k 2 · C B ⁡ &tgr; (9.2)
по веществу C

r C ⁡ &tgr; = &dd; &dd; ⁢ &tgr; ⁢ C C ⁡ &tgr; = k 2 · C B&tgr; ⁡ &tgr; - k 3 · C C ⁡ &tgr; (9.4)

и по вешеству D

r D ⁡ &tgr; = &dd; &dd; ⁢ &tgr; ⁢ C D ⁡ &tgr; = k 3 · C C ⁡ &tgr; (9.5),

найти зависимости концентрации каждого участника реакции от времени
C A ⁡ &tgr; , C B ⁡ &tgr; , C C ⁡ &tgr; , C D ⁡ &tgr; ( то есть решить каждое из приведенных дифферен-
циальных уравнений) и полученные зависимости подставить в уравнения (9.1 - 9.4)

Аналитическое решение этих дифференциальных уравнений (см., например:
Еремин Е.Н. Основы химической кинетики, М, Изд- во МГУ, 1971г. - с.59):

C A = C 0 · e - k 1 · &tgr; (9.6)

C B = C 0 · k 1 k 2 - k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; (9.7)

C C = C 0 · k 1 · k 2 k 2 - k 1 · k 3 - k 1 · e - k 1 · &tgr; + k 1 · k 2 k 1 - k 2 · k 3 - k 2 · e - k 2 · &tgr; + k 1 · k 2 k 1 - k 3 · k 3 - k 2 · e - k 3 · &tgr; (9.8)

Тогда, подставив (9.6.) в (9.1.), получим:

для скорости реакции по веществу А в зависимости от времени

- r A ⁡ &tgr; = &dd; &dd; ⁢ &tgr; ⁢ C A ⁡ &tgr; = - k 1 · C 0 · e - k 1 · &tgr; (9.9)

для скорости реакции по веществу B в зависимости от времени, подставив (9.6) в (9.2),:

r B ⁡ &tgr; = &dd; &dd; ⁢ &tgr; ⁢ C B ⁡ &tgr; = k 1 · C 0 · e - k 1 · &tgr; - k 2 · C 0 · k 1 k 2 - k 1 · e - k 1 · &tgr; - e - k 2 · &tgr; (9.10)

или после упрощений

r B ⁡ &tgr; = &dd; &dd; ⁢ &tgr; ⁢ C B ⁡ &tgr; = k 1 · C 0 · - exp ⁡ - k 1 · &tgr; · k 1 + k 2 · exp ⁡ - k 2 · &tgr; k 2 - k 1 (9.11)

Как можно заметить, точное аналитическое решение дифференциальных
уравнений (9.1 - 9.4) даже в простейшем случае реакций первого порядка
довольно громоздко.
В более сложных случаях, аналитическое решение уравнений может не
существовать или, если возможно, приведет к настолько грамоздким
выражениям, что практическое их использование становится крайне затруднительным.
Поэтому мы, как в свое время говорил один исторический персонаж, пойдем
другим путем и воспользуемся возможностями, представляемыми математическим
пакетом MathCAD, в частности, вычислительным блоком Given/Odesolve.

Ввод значений констант скоростей реакций.

k 1 &colon;=&Space; 0.44

k 2 &colon;=&Space; 0.2

k 3 &colon;=&Space; 0.1

Ввод времени (часы), в течение котрого исследуются зависимости концентрации и скорости реакций с интервалом в 1 час.

&tgr; &colon;=&Space; 0 , 1 .. 20

Given

Ввод ключевого слова.

Ввод кинетического уравнения, определяющего зависимость концентрации вещества А в реакции
A----> B ----> C -----> D

&dd; &dd; ⁢ &tgr; ⁢ C A ⁡ &tgr; = - k 1 · C A ⁡ &tgr;

Ввод начальной концентрации вещества А.

C A ⁡ 0 = 1

C A &colon;=&Space; Odesolve ⁡ &tgr; 20

Вывод результата - зависимость концентрации вещества А в реакции
A----> B ----> C -----> D

Рис. 9.1. Зависимость концентрации вещества А в реакции
A----> B ----> C -----> D

Теперь определим зависимость скорости реакции по веществу А от времени проведения процесса.

Ввод уравнения, определяющего зависимость
скорости реакции по веществу А в реакции
A----> B ----> C -----> D

r A ⁡ &tgr; &colon;=&Space; k 1 · C A ⁡ &tgr;

Вывод результата - зависимость скорости
реакции по веществу А в реакции
A----> B ----> C -----> D
Графичесая иллюстрация приведена на рис. 9.2.

Рис. 9.2. Зависимость скорости реакции по веществу А в реакции
A----> B ----> C -----> D

Теперь определим зависимость концентрации промежуточного вещества B и скорости реакции по веществу B от времени проведения процесса.

Given

Ввод кинетического уравнения, определяющего зависимость концентрации вещества B в реакции
A----> B ----> C -----> D

&dd; &dd; ⁢ &tgr; ⁢ C B ⁡ &tgr; = k 1 · C A ⁡ &tgr; - k 2 · C B ⁡ &tgr;

Ввод начальной концентрации вещества B

C B ⁡ 0 = 0

C B &colon;=&Space; Odesolve ⁡ &tgr; 20

Вывод результата - зависимость концентрации
вещества B в реакции
A----> B ----> C -----> D

Рис. 9.3. Зависимость концентрации вещества B
в реакции
A----> B ----> C -----> D

Ввод уравнения, определяющего зависимость
скорости реакции по веществу B в реакции
A----> B ----> C -----> D

r B ⁡ &tgr; &colon;=&Space; k 1 · C A ⁡ &tgr; - k 2 · C B ⁡ &tgr;

Вывод результата - зависимость скорости
реакции по веществу B в реакции
A----> B ----> C -----> D

Рис. 9.4. Зависимость скорости реакции по веществу B
в реакции в последовательной реакции
A----> B ----> C -----> D

Теперь определим зависимость концентрации промежуточного вещества C и скорости реакции A----> B ----> C -----> D по веществу C от времени проведения процесса .

Given

Ввод кинетического уравнения, определяющего зависимость концентрации вещества C в реакции
A----> B ----> C -----> D

&dd; &dd; ⁢ &tgr; ⁢ C C ⁡ &tgr; = k 2 · C B ⁡ &tgr; - k 3 · C C ⁡ &tgr;

C C ⁡ 0 = 0

Ввод начальной концентрации вещества C

C C &colon;=&Space; Odesolve ⁡ &tgr; 20

Вывод результата - зависимость концентрации
вещества C от времени проведения процесса в реакции
A----> B ----> C -----> D

Рис. 9.5;. Зависимость концентрации вещества C
в реакции
A----> B ----> C -----> D

Ввод уравнения, определяющего зависимость
скорости реакции по веществу C в реакции
A----> B ----> C -----> D

r C ⁡ &tgr; &colon;=&Space; k 2 · C B ⁡ &tgr; - k 3 · C C ⁡ &tgr;

Вывод результата - зависимость скорости
реакции по веществу C в реакции
A----> B ----> C -----> D

Рис. 9.6 Зависимость скорости реакции по веществу B
в реакции в последовательной реакции
A----> B ----> C -----> D

Наконец, определим зависимость концентрации продукта D и скорости реакции A----> B ----> C -----> D по продукту D от времени проведения процесса .

Given

Ввод кинетического уравнения, определяющего зависимость концентрации продукта D от времени в реакции
A----> B ----> C -----> D

&dd; &dd; ⁢ &tgr; ⁢ C D ⁡ &tgr; = k 3 · C C ⁡ &tgr;

C D ⁡ 0 = 0

Ввод начальной концентрации вещества D

C D &colon;=&Space; Odesolve ⁡ &tgr; 20

Вывод результата - зависимость концентрации
вещества D в реакции
A----> B ----> C -----> D

Рис. 9.7. Зависимость концентрации вещества B
от времени в реакции
A----> B ----> C -----> D

r D ⁡ &tgr; &colon;=&Space; k 3 · C C ⁡ &tgr;

Ввод уравнения, определяющего зависимость
скорости реакции по веществу D в реакции
A----> B ----> C -----> D

Вывод результата - зависимость скорости
реакции по веществу D от времени в реакции
A----> B ----> C -----> D

Рис. 9.8. Зависимость скорости реакции по веществу D от времени в реакции
A----> B ----> C -----> D

В заключение приведем графики, иллюстрирующие сравнительный ход зависимостей концентраций и скоростей реакции A----> B ----> C -----> D

Рис. 9.9 . Зависимость концентрации веществ от времени в реакции
A----> B ----> C -----> D

Рис. 9.10. Зависимость скорости реакции по веществам от времени в реакции
A----> B ----> C -----> D

Задача 3.10
Фотохимическое хлорирование в избытке хлора ( его концентрацию можно считать постоянной) 3,4,5 - трихлор - 2(трихлорметил) пиридина ( в дальнейшем вещество А) можно рассматривать ка реакцию первого порядка, протекающую по последовательно - параллельной схеме

k 1 k 3
A --------> B ------------> D
A --------->C ------------> D
k 2 k 4
При 433К по данным Емельянова В.И., Стуля Б.Я., Королева Б.М. ( Кинетика и катализ, 1984.-т.25, №3) константы скорости соответственно равны k 1 =0.792, k 2 = 0.252, k 3 = 0.324 и k 4 = 0.792 1/ч.
Рассчитайте концентрации промежуточеных и конечных продуктов в зависимости от времени протекания процесса и постройте кинетические кривые.

Решение.

Кинетические уравнения в дифференциальной форме для участников реакции имеют вид:
r A = &dd; &dd; ⁢ &tgr; ⁢ C A = - k 1 + k 2 · C A (10.1)

r B = &dd; &dd; ⁢ &tgr; ⁢ C B = k 1 · C A - k 3 · C B (10.2.)

r C = &dd; &dd; ⁢ &tgr; ⁢ C C = k 2 · C A - k 4 · C C (10.3.)

r D = &dd; &dd; ⁢ &tgr; ⁢ C D = k 3 · C B + k 4 · C C (10.4.)

Будем решать систему дифференциальных уравнений (10.1 - 10.4.) методом Рунге - Кутты с фиксированным шагом с помощью имеющейся в MathCAD встроенной функции rkfixed(y0, t0, t1, M, D), где
y0 - вектор начальных значений в точке t0,
t0 - начальная точка расчета,
t1 - конечная точка расчета,
M - число шагов, на которых численный метод находит решение,
D - векторная функция размера N · 1 двух аргументов - скалярного и векторного, при этом y - искомая векторная функция аргумента t того же размера.
Для удобства введем обозначения: C 0 - текущая концентрация вещества A,
C 1 - концентрация вещества B, C 2 - концентрация вещества C и C 3 - концентрация вещества D.
Тогда:

Ввод значений констант скоростей

k 1 &colon;=&Space; 0.792

k 2 &colon;=&Space; 0.252

Важное замечание:Вы можете изменить значения констант и проследить их влияние на кинетические кривые .

k 3 &colon;=&Space; 0.324

k 4 &colon;=&Space; 0.792

Ввод системы дифференциальных уравнений - кинетических уравнений последовательно - параллельной реакции
A --------> B ------------> D
A --------->C ------------> D.

D ⁡ &tgr; C &colon;=&Space; ( - k 1 + k 2 · C 0 k 1 · C 0 - k 3 · C 1 k 2 · C 0 - k 4 · C 2 k 3 · C 1 + k 4 · C 2 )

Во второй строке листинга определен вектор начальных условий.

C0 &colon;=&Space; ( 1 0 0 0 )

В третьей строке листинга определено число шагов, на которых рассчитывается решение.

M &colon;=&Space; 100

Последняя строка присваевает матричной переменной u результат действия функции rkfixed.
Решение системы будет осуществлено на промежутке (0,10)

u &colon;=&Space; rkfixed ⁡ C0 0 10 M D

Обратите внимание на разно- чтение в обозначении индексов вектора начальных условий и матрицы решения.
В первом столбце матрицы собраны зна- чения нулевой компоненты ис- комого вектора � 0 , во втором столбце - первой компоненты C 1 и т.д.

Просмотреть все компонены матрицы, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки.

Максимальное значение кон-
центрации вещества В C 1 = =0.448 моль/л достигается при времени t = 1.6ч., а максималь- ное значение концентрации вещества C C 2 = 0.101 моль/л через t= 1ч.

Рис. 9.9 . Зависимость концентрации веществ от времени в реакции
A----> B ----> C -----> D

Рис. 10.1. Кинетические кривые исходного вещества (1), промежуточных соединений (2,3) и продукта (4) при протекании последовательно - параллельной реакции
A --------> B ------------> D
A --------->C ------------> D

Сравните положение максимумов промежуточных продуктов на кинетических кривых последовательной реакции
A -----> B ---->C ----> D
(см. предыдущую задачу, рис. 9.9 ) и последовательно - параллельной реакции

A --------> B ------------> D
A --------->C ------------> D
Может ли положение максимумов служить косвенным свидетельством в пользу последовательного или последовательно - параллельного механизма реакции?

Задача 3.11.
При исследовании разложения глюкозы в водном растворе при температуре 350К были получены следующие результаты по зависимости концентрации глюкозы от времени протекания процесса

Время, мин. 0 45 120 240 480 960 1440 1920 2880 концентрация,
моль/ л 56.0 55.3 54.2 52.5 49.0 43.2 38.0 33.1 26.0

Определите порядок реакции, рассчитайте константу скорости при этой температуре, время полупревращения и время достижения степени превращения c = 0.99.

Решение.

Рассматриваемая реакция принадлежит к реакциям вида

A -------> Продукты,

кинетическое уравнение которой в дифференциальной форме имеет вид:

r A = - &dd; &dd; ⁢ &tgr; ⁢ C A = k · C A n , (11.1)
где n - порядок реакции и k - константа скорости.
Тогда время достижения заданной концентрации C

, (11.2)
ãде C 0 - концентрация исходного вещества при t = 0.
Åсли порядок реакции n =1, то интегрирование (11. 2) приводит к выражению

&tgr; = 1 k · ln ⁡ C 0 C (11.3.)

Если порядок реакции отличен от единицы, т.е. n ≠ 1 , то интегрирование (11. 2) для любого n ≠ 1 приводит к выражению

&tgr; = � 1 - n - C o 1 - n k · n - 1 (11.4)
и. например, для n = 2

&tgr; = 1 k · 1 C - 1 C 0 (11.5)

Поскольку константа скорости не зависит от концентрации , ее постоянство при различных значениях времени и соответствующему этому времени концентрации вещества может служить критерием, по которому определяется порядок реакции.
Так, например, из (11.3.), то есть для реакций первого порядка

k = 1 &tgr; · ln ⁡ C 0 C (11.6),
из (11.5.) дл реакций второго порядка

k = 1 &tgr; · 1 C - 1 C 0 (11.7.)

и для любого порядка, отличного от единицы

k = � 1 - n - C o 1 - n &tgr; · n - 1 (11.8)

Предположим первый порядок реакции, тогда при подстановке в соотношение (11.6)
k = 1 &tgr; · ln ⁡ C 0 C

значений времени и соответствующих этому времени значений концентраций константа скорости реакции в пределах ошибки эксперимента должна остоваться постоянной.
Проверим это:

C 0 &colon;=&Space; 56.0

k ⁡ &tgr; C &colon;=&Space; 1 &tgr; · log ⁡ C 0 C · 2.3

Рассчитаем значение константы скорости при различных t и соответствующих этим значениям концентраций глюкозы, подставив в (11.6) экспериментальные значения.

i &colon;=&Space; 0 .. 7

k 1 ⁡ &tgr; C &colon;=&Space; 1 &tgr; · ln ⁡ C 0 C

&tgr; ⁡ i &colon;=&Space; ( 45 120 240 480 960 1440 1920 2880 )

C ⁡ i &colon;=&Space; ( 55.3 54.2 52.5 49.0 43.2 38.0 33.1 26.9 )

k ⁡ &tgr; C &colon;=&Space; 1 &tgr; · log ⁡ C 0 C · 2.3

k = function

Ïîëó÷åííûå ðåçóëüòàòû ñâèäåòåëüñòâóþò î ïîñòîÿííîì - â ïðåäåëàõ îøèáêè ýêñïåðèìåíòà -
çíà÷åíèè êîíñòàíòû ñêîðîñòè.
Ýòî îçíà÷àåò, ÷òî ïðåäïîëîæåíèå î ïåðâîì ïîðÿäêå ðåàêöèè ñïðàâåäëèâî.

Ðàññ÷èòàåì ñðåäíåå çíà÷åíèå êîíñòàíòû ñêîðîñòè.

2.792 · 10 - 4 + 2.72 · 10 - 4 + 2.686 · 10 - 4 + 2.686 · 10 - 4 + 2.779 · 10 - 4 + 2.7 · 10 - 4 + 2.69 · 10 - 4 7 = 2.722 · 10 - 4

Мы установили, что исследуемая реакция разложения глюкозы является реакцией первого порядка и ее кинетическое уравнение в дифференциальной форме - с учетом найденного значения константы скорости - можно выразить соотношением (где C 1 - обозначение рассчетного значения концентрации глюкозы, в отличии от С - ее экспериментального значения, приведенного в условии задачи).
r = - &dd; &dd; ⁢ &tgr; ⁢ C 1 = 2.72 · 10 - 4 · C 1 (11.9)
Или через степень превращения

r = &dd; &dd; ⁢ &tgr; ⁢ χ = 2.72 · 10 - 4 · 1 - χ (11.10)

Кинетическое уравнение в интегральной форме

C 1 ⁡ &tgr; = C 0 · e - 2.72 · 10 - 4 · &tgr; , (11.11)
где C 0 - начальная концентрация исходного вещества.
Или через степень превращения c

χ ⁡ &tgr; = 1 - e - 2.72 · 10 - 4 · &tgr; (11.12)

Из (11.10) или из (11.12) можно определить время достижения некоторой заданной степени превращения:

(11.13)

Рассчитаем согласно (11.11) значения концентрации глюкозы в зависимости
от времени проведения процесса и сравним полученные результаты с экспериментальными, приведенными в условии задачи.

Ввод начальной концентрации и значения константы скорости реакции.

C 0 &colon;=&Space; 56

k &colon;=&Space; 2.72 · 10 - 4

Ввод времени, при котором будет рассчитана концентрация исходного вещества в исследуемой реакции разложения глюкозы в водном растворе при температуре 350К

&tgr; &colon;=&Space; ( 0 45 120 240 480 960 1440 1920 2880 )

Ввод соотношения, определяющего зависимость концентрации исходного вещества в реакции первого порядка.

C 1 ⁡ &tgr; &colon;=&Space; C 0 · e - k · &tgr;

Вывод результата счета - концентрация глюкозы в зависимости от времени проведения процесса.

&tgr; &colon;=&Space; ( 0 45 120 240 480 960 1440 1920 2880 )

C 1 ⁡ &tgr; = ( 56 55.319 54.202 52.461 49.146 43.131 37.852 33.219 25.585 )

Ввод экспериментальных значений
зависимости концентрации глюкозы
в реакции ее разложения в водном
растворе при температуре 350К

C ⁡ &tgr; &colon;=&Space; ( 56.0 55.3 54.2 52.5 49.0 43.2 38.0 33.1 26.0 )

Ðèñ.11.1 Çàâèñèìîñòü êîíöåíòðàöèè ãëþêîçû îò âðåìåíè â ðåàêöèè åå ðàçëîæåíèÿ â âîäíîì ðàñòâîðå ïðè òåìïåðàòóðå 350Ê ( Ñ - ýêñïåðèìåíòàëüíûå ðåçóëüòàòû, C 1 - ðåçóëüòàòû ðàñ÷åòà ïî êèíåòè÷åñêîìó óðàâíåíèþ ïåðâîãî ïîðÿäêà.)

Теперь, согласно (11.12):

χ ⁡ &tgr; = 1 - e - 2.72 · 10 - 4 · &tgr;

рассчитаем зависимость степени превращения от времени протекания процесса.

Ввод времени (мин.), в течение которого будет исследована зависимость степени превращения глюкозы ( с интервалом в 100 мин.)

&tgr; &colon;=&Space; 0 , 100 .. 10000

Ввод соотношения, определяющего зависимость степени превращения исходного вещества в необратимой реакции первого порядка от времени протекания процесса.

k &colon;=&Space; 2.72 · 10 - 4

χ ⁡ &tgr; &colon;=&Space; 1 - e - k · &tgr;

Âàæíîå çàìå÷àíèå:
Âû ìîæåòå îïðåäåëèòü ñòåïåíü ïðåâðàøåíèÿ äëÿ ëþáîãî âðåìåíè ïðîòåêàíèÿ ïðîöåññà.

Ðèñ.11.2. Çàâèñèìîñòü ñòåïåíè ïðåâðàùåíèÿ ãëþêîçû îò âðåìåíè â ðåàêöèè åå ðàçëîæåíèÿ â âîäíîì ðàñòâîðå ïðè òåìïåðàòóðå 350Ê.

И, наконец, определим время достижения степени превращения c= 0.99 согласно (11.13)

χ &colon;=&Space; 0.99

Âàæíîå çàìå÷àíèå:
Âû ìîæåòå îïðåäåëèòü âðåìÿ äîñòèæåíèÿ ëþáîé ñòåïåíè ïðåâðàùåíèÿ.

&tgr; ⁡ χ = 1.693 · 10 4

ìèí.

Задача 3.12
При исследовании кинетики реакции димеризации бутадиена при температуре 599К

2 C 2 · H 6 -------> C 8 · H 12
были получены следующие данные об изменении общего давления системы P(мм.рт.ст.) от времени t (мин)

Определите скорость реакции в каждый момент времени, порядок реакции по бутадиену и константу скорости реакции при исследуемой температуре.

&tgr; &colon;=&Space; ( 0 5 10 15 20 25 30 35 40 45 )

P &colon;=&Space; ( 632 590 552 515 485 458 435 414 396 378 )

Решение.
Для расчета скорости реакции, а так же порядка реакции и константы скорости необходимо в каждый момент времени знать величину давления p(t) бутадиена, которое может быть рассчитано как

p ⁡ &tgr; = 2 · P ⁡ &tgr; - P 0 , (12.1)
где p ⁡ &tgr; , P ⁡ &tgr; и P 0 - парциальное давление бутадиена, общее давление в системе в момент времени t и давление в системе в начальный момент.
Тогда, согласно (12.1) рассчитаем парциальное давëение бутадиена в момент времени t

Ввод начального общего давления P 0 &colon;=&Space; 632 и общего давления в момент времени t P ⁡ &tgr;. .

P 0 &colon;=&Space; 632

P ⁡ &tgr; &colon;=&Space; 458

Ввод соотношения, определяющего связь между парциальным давлением бутадиена p ⁡ &tgr; , общим давлением в системе P ⁡ &tgr; и давлением в системе P 0 в начальный момент

p ⁡ &tgr; &colon;=&Space; 2 · P ⁡ &tgr; - P 0

p ⁡ &tgr; = 284

Вывод результата - давление бутадиена в момент времени t

Теперь построим график зависимости парциального давления бутадиена от времени проведения процесса

Вывод результата - давление бутадиена p ⁡ &tgr; в реакции его димеризации при температуре 599К
2 C 2 · H 6 -------> C 8 · H 12 â зависимости от времени t

&tgr; &colon;=&Space; ( 0 5 10 15 20 25 30 35 40 45 )

p ⁡ &tgr; &colon;=&Space; ( 632 548 472 398 338 284 238 196 160 124 )

Рис.12.1. Зависимость парциального давления (мм.рт.ст.) бутадиена от времени проведения процесса его димеризации при 599К.

Предположим, что скорость реакции димеризации бутадиена описывается кинетическим уравнением вида
r = - &dd; &dd; ⁢ &tgr; ⁢ p = k · p n (12.2)

Одним из путей решения поставленной задачи - определении скорости реакции в зависимости от времени и нахождении порядка реакции и константы скорости - может быть следующий:
-- с помощью комбинации встроенной функции regress и полиномиальной интерполяцией найдем аналитический вид функции p(t), заданной табличными значениями,
-- найдем производную полученной функции по времени, т. е. тем самым определим скорость реакции как функцию времени и значение скорости реакции в любой момент времени,
-- построим систему уравнений вида (12.2) и решим ее относительно k и n, а значит найдем порядок реации и рассчитаем значение константы скорости и кинетическое уравнение реакции,
-- по найденному кинетическому уравнению рассчитаем давление бутадиена в заданные моменты времени и сопоставим полученный результат с экспериментальным, представленным в условии задачи.

1. Определим аналитический вид функции p(t), заданной табличными значениями.

&tgr; &colon;=&Space; ( 0 5 10 15 20 25 30 35 40 45 ) T

Ввод транспонированных матриц значений времени давления бутадиена.

p &colon;=&Space; ( 632 590 552 515 485 458 435 414 396 378 ) T

Здесь к - степень полинома регрессии.

k &colon;=&Space; 2

regress ⁡ &tgr; p k - вектор коэффициентов для построения полиномиальной регрессии данных; t - вектор действительных данных аргумента, элементы которого расположены в порядке возрастания, p - вектор действительных данных значений

s &colon;=&Space; regress ⁡ &tgr; p k

p 1 ⁡ t &colon;=&Space; interp ⁡ s &tgr; p t

interp ⁡ s &tgr; p t - результат полиномиальной регрессии;
s = regress ⁡ &tgr; p k , t - значение аргумента полинома регрессии.

Применение комбинации встроенной функции regress и полиномиальной интерполяции приводит к следующему аналитическому виду функции p(t):

s = ( 3 3 2 631.164 - 8.604 0.067 )

p 1 ⁡ &tgr; &colon;=&Space; 631.16 - 8.604 · &tgr; + 0.067 · &tgr; 2

Сравнение экспериментальных данных, приведенных в
условии задачи (p), и рассчитанных по уравнению регрессии ( p 1 ⁡ t иллюстрирует рис. 12.2.

p 1 ⁡ t &colon;=&Space; ( 631.16 589.82 551.85 517.24 485.99 458.10 433.58 412.42 394.6 380.20 )

Рис.12.2. Сравнение экспериментальных (p) и рассчитанных по уравнению регрессии ( p 1 ) данных по давлению бутадиена в зависимости от времени.

Теперь определим скорость реакции.
Поскольку зависимость давления бутадиена от времени можно описать функцией
вида
p 1 ⁡ &tgr; = 631.16 - 8.604 · &tgr; + 0.067 · &tgr; 2 (12.3)
и скорость реакции по бутадиену
r = - &dd; &dd; ⁢ &tgr; ⁢ p , (12.4)
то после дифференциирования (12.3) зависимость скорости реакции от времени

r = 8.604 - 0.134 · &tgr; (12.5)

Постороим графики зависимости скорости реакции от времени (рис. 12.3) и от давления бутадиена (рис. 12.4).

&tgr; &colon;=&Space; 0 , 5 .. 45

r ⁡ &tgr; &colon;=&Space; 8.604 - 0.134 · &tgr;

Ââîä ñîîòíîøåíèé, îïðåäåëÿþùèõ çàâèñèìîñòü ñêîðîñòè ðåàêöèè r ⁡ &tgr; è äàâëåíèÿ áóòàäèåíà p 1 ⁡ &tgr; îò âðåìåíè ïðîâåäåíèÿ ïðîöåññà.

p 1 ⁡ &tgr; &colon;=&Space; 631.16 - 8.604 · &tgr; + 0.067 · &tgr; 2

Âûâîä ðåçóëüòàòà - çàâèñèìîñòü ñêîðîñòè ðåàêöèè r ⁡ &tgr; îò âðåìåíè ïðîâåäåíèÿ ïðîöåññà.

Вывод результата - çàâèñèìîñòü äàâëåíèÿ áóòàäèåíà p 1 ⁡ &tgr; îò âðåìåíè ïðîâåäåíèÿ ïðîöåññà.

Графическая иллюстрация полученных результатов приведена на рис. 12.3 и12.4.

Рис. 12.3. Зависимость скорости реакции димеризации бутадиена от времени проведения процесса..

Рис. 12.4. Скорость реакции димеризации бутадиена в зависимости от давления бутадиена.

Теперь определим порядок реакции и константу скорости.
Для этого составим систему из десяти уравнений с двумя неизвестнами - порядком реакции n и константой скорости реакции k - вида

r = k · p n

по полученным ранеее данным о парциальном давлении бутадиена в зависимости от времени p 1 ⁡ &tgr; и скорости реакции в зависимости от времени r ⁡ &tgr;

Iiiyooy i oii, ?oi yenia?eiaioaeuiue ?aca?in ii?ao auou ainoaoi?iui, n?aco oiaiuoei cia?aiea CTOL

CTOL &colon;=&Space; 0.85

Íà÷àëüíûå çíà÷åíèÿ ïåðåìåííûõ, îòíîñèòåëüíî êîòîðûõ áóäåì ðåøàòü ñèñòåìó óðàâíåíèé.

n &colon;=&Space; 1

k &colon;=&Space; 10 - 3

Given

k · 631.16 n = 8.60

k · 589.81 n = 7.93

k · 551.82 n = 7.264

k · 517.17 n = 6.594

Ввод системы уравнений.

k · 485.88 n = 5.92

k · 457.93 n = 5.25

k · 433.34 n = 4.58

k · 412.09 n = 3.91

k · 394.2 n = 3.244

k · 379.65 n = 2.57

Ðåçóëüòàò ðåøåíèÿ ñèñòåìû óðàâíåíèé.

Поскольку значение порядка реакции n близко к двум, можно считать, что димеризация бутадиена подчиняется кинетическому уравнению второго порядка.
Учтя это, найдем уточненное значение константы скорости реакции, для чего решим предыдущую систему уравнений при n = 2, то есть систему из 10 уравнений, но уже с одним неизвестным - константой скорости реакции k.

k &colon;=&Space; 3 · 10 - 5

Ввод уравнения f ⁡ k = k · p 1 ⁡ &tgr; 2 - r ⁡ &tgr; при значениях p ⁡ &tgr; и r ⁡ &tgr; соответствующих времени t = 25 ìèí.

f ⁡ k &colon;=&Space; k · 457.93 2 - 5.25

solution &colon;=&Space; root ⁡ f ⁡ k k

Вывод результата - значение константы скорости реакции при значениях p ⁡ &tgr; и r ⁡ &tgr; соответствующих времени t = 25 ìèí.

solution = 2.504 · 10 - 5

k &colon;=&Space; ( 2.159 · 10 - 5 2.28 · 10 - 5 2.386 · 10 - 5 2.465 · 10 - 5 2.508 · 10 - 5 2.504 · 10 - 5 2.439 · 10 - 5 2.302 · 10 - 5 2.088 · 10 - 5 1.783 · 10 - 5 )

2.159 + 2.28 + 2.386 + 2.465 + 2.508 + 2.504 + 2.439 + 2.302 + 2.088 + 1.783 10 = 2.291

Таким образом, среднеее значение константы скорости

k 1 = 2.3 · 10 - 5
Тогда кинетическое уравнение реакции димеризации бутадиена при 595К

r = - &dd; &dd; ⁢ &tgr; ⁢ p = 2.3 · 10 - 5 · p 2 (12.5)

А значит изменение давления бутадиена в зависимости от времени можно описать соотношением

p ⁡ &tgr; = p 0 1 + k · p 0 · &tgr; (12.6)
Cравним теперь экспериментальные результаты по изменению давления бутадиена со временем p(t) в результате реакции его димеризации (см. условие задачи) с полученными p 2 ⁡ &tgr; по уравнению (12.6)

&tgr; &colon;=&Space; 0 , 5 .. 45

p 0 &colon;=&Space; 632

Çäåñü p(t) - ýêñïåðèìåíòàëüíûå äàííûå î çàâèñèìîñòè äàâëåíèÿ áóòàäèåíà, ïðåäñòàâëåííûå â óñëîâèè çàäà÷è.

p 2 ⁡ &tgr; &colon;=&Space; p 0 1 + 2.3 · 10 - 5 · p 0 · &tgr;

&tgr; &colon;=&Space; ( 0 5 10 15 20 25 30 35 40 45 )

p ⁡ &tgr; &colon;=&Space; ( 632 590 552 515 485 458 435 414 396 378 )

Ðèñ.12.5. Ñðàâíåíèå ýêñïåðèìåíòàëüíûõ (p(t)) è ðàñ÷åòíûõ äàííûõ p 2 ⁡ &tgr;
ïî èçìåíåíèþ äàâëåíèÿ áóòàäèåíà â ïðîöåññå åãî äèìåðèçàöèèþ

Задача 3.13.
При 1300К константы скорости параллельных бимолекулярных реакций
k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .

равны k 1 =25.7л/моль с и k 2 = 18.2 л/моль с
Рассчитайте изменение концентраций веществ со временем, если исходная концентрация оксида азота C 0 = 4 моль/л

Решение.
Решение задачи с помощью инструментария Mathcad довольно просто: достаточно коррректно записать систему кинетических уравнений в дифференциальной форме и решить эту систему.
Тогда
скорость реакции по оксиду азота:

r NO = r 1 = - &dd; &dd; ⁢ &tgr; ⁢ C NO = k 1 + k 2 · C 0 2 (13.1)
Скорость реакции по молекулярному азоту:

r N 2 = r 2 = &dd; &dd; ⁢ &tgr; ⁢ C N 2 = k 1 · C 0 2 (13.2)
Скорость реакции по закиси азота:

r N 2 · 0 = r 3 = &dd; &dd; ⁢ &tgr; ⁢ C N 2 · 0 = k 2 · C 0 2 (13.3)

Скорость реакции по молекулярному кислороду:

r O 2 = r 4 = &dd; &dd; ⁢ &tgr; ⁢ C O 2 = k 1 · C 0 2 + 0.5 · k 2 · C 0 2 (13.4)

Остается только решить эту систему дифференциальных уравнений.
В Mathcad имеется несколько встроенных функций, позволяющие решить поставленную задачу различными численными методами.
Будем решать систему (13.1) - (13.4.) с помощью встроенной функции rkfixed(y0, t0, t1, M, D), реализующуй метод Рунге - Кутты с фиксированным шагом.
Здесь y0 - вектор начальных значений в точке t0, t0 - начальная точка расчета, t1 - конечная точка расчета, M - число шагов, на которых численный метод находит решение и D - векторная функция двух аргументов - скалярного t и векторного y.
Функция rkfixed(y0, t0, t1, M, D) выдает решение в виде матрицы, в левом столбце которой находятся значения аргумента t, делящие интервал на равные шаги, а в остальных стобцах - значения искомых функций y 0 ⁡ t , y 1 ⁡ t и т.д., рассчитанные для этих значений аргумента.

Ввод значений констант скоростей реакций.
Вы можете изменить эти значения и проследить,как это скажется на ходе зависимостей концентраций ре-
агирующих веществ от времени.

k 1 &colon;=&Space; 25.7

k 2 &colon;=&Space; 18.2

Система кинетических уравнений (13.1 - 13.4) исследуемых параллельных бимолекулярных реакций k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .
в дифференциальной форме.

D ⁡ &tgr; C &colon;=&Space; ( - k 1 + k 2 · C 0 2 k 1 · C 0 2 k 2 · C 0 2 k 1 · C 0 2 + 0.5 · k 2 · C 0 2 )

Ввод начальных условий.
Вы можете изменить эти значения и проследить,как это скажется на ходе зависимостей концентраций реагирующих веществ от времени.

C0 &colon;=&Space; ( 4 0 0 0 )

Ввод числа шагов, на которых численный метод находит решение.

M &colon;=&Space; 100

u &colon;=&Space; rkfixed ⁡ C0 0 0.4 M D

Присваивание матричной переменной u
результат действия функции rkfixed.

Результат решения системы.
Просмотреть все компоненты матрицы, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки.
В матрице u: u1- концентрация исходного вещества оксида азота,u2 - концентрация молекулярного азота, u3- концентрация закиси азота и u4 - концентрация молекулярного кислорода.

Графическая иллюстрация полученных результатов приведена на рис.13.1 - 13.4.

Рис. 13.1. Зависисость концентрации
исходного вещества от времени в реакции
k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .

Рис. 13.2. Зависисость концентрации молекулярного азота от времени в реакции
k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .

Рис. 13.3. Зависисость концентрации
закиси азота от времени в реакции
k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .

Рис. 13.4. Зависисость концентрации
молекулярного кислорода от времени в реакции
k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .

Рис. 13.5. Зависисость концентрации исходного вещества u < 1 > , молекулярного азота u < 2 > , закиси азота u < 3 > и молекулярного кислорода u < 4 > от времени в реакции
k 1 N 2 + O 2
2 · NO ===>
k 2 N 2 · 0 + 0.5 · O 2 .
Êîíñòàíòû ñêîðîñòè ñîîòâåòñòâåííî ðàâíû k 1 &colon;=&Space; 25.7 è k 2 &colon;=&Space; 18.2

Задача 3.14.

Скорость реакции

2NO + Cl2 ------> 2NOCl

описывается кинетическим уравнением третьего порядка

r NO = - &dd; &dd; ⁢ &tgr; ⁢ C NO = 4.6 · 10 9 · e - 15500 R · T · C NO 2 · C Cl 2

14.1

Определите зависимость концентраций исходных веществ и продукта реакции от времени при двух температурах.
Для тех же температур рассчитайте время достижения степени превращения NO c = 0.8.
Проследите, как влияет время проведения процесса на степень превращения.
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.02 и молекулярного хлора - 0.035.

Решение.
Решение задачи с помощью инструментария Mathcad довольно просто: достаточно коррректно записать систему кинетических уравнений в дифференциальной форме и решить эту систему.
Тогда
скорость реакции по оксиду азота:

r NO = - &dd; &dd; ⁢ &tgr; ⁢ C NO = - &dd; &dd; ⁢ &tgr; ⁢ C 0 = k · C NO 2 · C Cl 2 (14.1)
или, введя обозначения, C NO = C 0 и C Cl 2 = C 1

&dd; &dd; ⁢ &tgr; ⁢ C 0 = - k · C 0 2 · C 1 (14.2)

Скорость реакции по молекулярному хлору:

r Cl 2 = - &dd; &dd; ⁢ &tgr; ⁢ C NO = - &dd; &dd; ⁢ &tgr; ⁢ C 1 = 0.5 · k · C NO 2 · C Cl 2 (14.3)

или с учетом приняиых обозначений

&dd; &dd; ⁢ &tgr; ⁢ C 1 = - 0.5 · k · C 0 2 · C 1 (14.4)

И скорость по продукту реакции ( введя обозначение � NOCl = C 2 )

r NOCl = &dd; &dd; ⁢ &tgr; ⁢ C NOCl = k · C NO 2 · C Cl 2 (14.5)

или

r NOCl = &dd; &dd; ⁢ &tgr; ⁢ C 2 = k · C 0 2 · C 1 (14.6)

Остается только решить эту систему дифференциальных уравнений.
В Mathcad имеется несколько встроенных функций, позволяющие решить поставленную задачу различными численными методами.

Будем решать систему (14.2; 14.4; 14.6) с помощью встроенной функции rkfixed(y0, t0, t1, M, D), реализующуй метод Рунге - Кутты с фиксированным шагом. Здесь y0 - вектор начальных значений в точке t0, t0 - начальная точка расчета, t1 - конечная точка расчета, M - число шагов, на которых численный метод находит решение и D - векторная функция двух аргументов - скалярного t и векторного y.
Функция rkfixed(y0, t0, t1, M, D) выдает решение в виде матрицы, в левом столбце которой находятся значения аргумента t, делящие интервал на равные шаги, а в остальных стобцах - значения искомых функций y 0 ⁡ t , y 1 ⁡ t и т.д., рассчитанные для этих значений аргумента.

Значения температуры и энергии активации реакции.
Вы можете изменить эти значения и проследить,как это скажется на ходе зависимостей концентраций ре-
агирующих веществ от времени.

R &colon;=&Space; 8.31

T &colon;=&Space; 273

E &colon;=&Space; 15500

Ñèñòåìà êèíåòè÷åñêèõ óðàâíåíèé â
äèôôåðåíöèàëüíîé ôîðìå.

D ⁡ &tgr; C &colon;=&Space; ( - 4.6 · 10 9 · e - E R · T · C 0 2 · C 1 - 0.5 · 4.6 · 10 9 · e - E R · T · C 0 2 · C 1 4.6 · 10 9 · e - E R · T · C 0 2 · C 1 )

C0 &colon;=&Space; ( 0.02 0.035 0 )

Ввод числа шагов, на которых численный метод находит решение.

M &colon;=&Space; 100

Присваивание матричной переменной u результат действия функции rkfixed.

u &colon;=&Space; rkfixed ⁡ C0 0 0.01 M D

Результат решения системы.
Просмотреть все компоненты матрицы, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки.
В матрице u:
u1 - концентрация исходного вещества оксида азота, u2 - концентрация молекулярного хлора, u3 - крнцентрация продукта реакции.

Графическая иллюстрация полученных результатов приведена на рис.14.1 - 14.3.

Рис. 14.1. Зависимость концентрации
исходного вещества оксида азота
от времени в реакции 2 · NO + Cl 2 ===> 2 NOCl ïðè 273Ê.
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.02 и молекулярного хлора - 0.035. .

Рис. 14.2. Зависимость концентрации
исходного вещества молекулярного
хлора от времени в реакции
2 · NO + Cl 2 ===> 2 NOCl
ïðè 273Ê.
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.2 и молекулярного хлора - 0.5.

Рис. 14.1. Зависимость концентрации исходного вещества оксида азота u < 1 > , молекулярного хлора u < 2 > и продукта реакции u < 3 > от времени проведения процесса в реакции
k
2 · NO + Cl 2 ===> 2 NOCl
при 273К.
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.02 и молекулярного хлора - 0.035.

Рис. 14.3. Зависимость концентрации
продукта реакции от времени в реакциè 2 · NO + Cl 2 ===> 2 NOCl
ïðè 273Ê.
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.02 и молекулярного хлора - 0.035.

Теперь рассмотрим влияние времени проведения процесса на степень превращения, например, оксида азота.
Напомним, что степень превращения c определяется соотношением

χ ⁡ &tgr; = � 0 - C ⁡ &tgr; C 0 ,
где C 0 , C ⁡ &tgr; - начальная концентрация некоторого компонента и его концентрация в момен времени t.

Тогда
2 · NO + Cl 2 ===> 2 NOCl

èñõîäíàÿ êîíöåíòðàöèÿ C 01 C 02 0
ïðîðåàãèðîâàëî ê ìîìåíòó t C 01 · χ 0.5 · C 01 · χ
êîíöåíòðàöèÿ â ìîìåíò
âðåìåíè t C 01 · 1 - χ C 02 - 0.5 · C 01 · χ

Тогда скорость реакции по оксиду азота можно выразить соотношением

- &dd; &dd; ⁢ &tgr; ⁢ C NO = k · C NO 2 · C Cl 2 = k · C 01 · 1 - χ 2 · C 02 - 0.5 · C 01 · χ (14.7)

Откуда время достижения некоторой степени превращения c

(14.8)

Ввод диапазона значений степени превращения, в котором будет исследовано время достижения.
Степень превращения изменяется от 0 до 0.99 с интервалом 0.01.

χ &colon;=&Space; 0 , 0.01 .. 0.99

R &colon;=&Space; 8.31

T &colon;=&Space; 273

E &colon;=&Space; 15500

Ввод значений энергии активации и началных концентраций NO C 01 и Cl 2 C 02

C 01 &colon;=&Space; 0.02

C 02 &colon;=&Space; 0.035

Ввод соотношения, определяющего зависимость времени достижения степени превращения NO c в реакции
2 · NO + Cl 2 ===> 2 NOCl

&tgr; ⁡ χ &colon;=&Space; ∫ 0 χ 1 4.6 · 10 9 · e - E R · T · C 01 2 · 1 - χ 2 · C 02 - 0.5 · C 01 · χ &dd; χ

Вывод результата счета -зависимость времени достижения степени превращения NO c в реакции
2 · NO + Cl 2 ===> 2 NOCl
Просмотреть все компоненты c и t(c), которые не помещаются на экране, в частности, те, которые заданы в условии задачи, можно с помощью вертикальной полосы прокрутки.

Ðèñ. 14.4. Çàâèñèìîñòü âðåìåíè äîñòèæåíèÿ ñòåïåíè ïðåâðàùåíèÿ ïðè 273Ê â ðåàêöèè
2 · NO + Cl 2 ===> 2 NOCl
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.02 и молекулярного хлора - 0.035.

Ðèñ. 14.5. Çàâèñèìîñòü ñòåïåíè ïðåâðàùåíèÿ èñõîäíîãî âåùåñòâà NO ïðè 273Ê. îò âðåìåíè â ðåàêöèè
2 · NO + Cl 2 ===> 2 NOCl
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.02 и молекулярного хлора - 0.035.

Рассчитаем (как просили сделать в условии задачи) время достижения степени превращения NO c = 0.8 при температуре 273К.

&tgr; ⁡ 0.8 = 0.07

Теперь исследуем влияние температуры на время достижения заданной степени превращения и влияние температуры на степень превращения в зависимости от времени поведения процесса.

χ 1 &colon;=&Space; 0 , 0.01 .. 0.99

Ввод температуры, при которой будет исследована зависимость степени превращения от времени проведения процеса.
Вы можете ввести другое значение температуры и проследить изменение хода зависимости степень превращения - время.

T &colon;=&Space; 323

Ввод соотношения, определяющего зависимость времени достижения степени превращения NO χ 1 в реакции
2 · NO + Cl 2 => 2 NOCl

&tgr; 1 ⁡ χ 1 &colon;=&Space; ∫ 0 χ 1 1 4.6 · 10 9 · e - E R · T · C 01 2 · 1 - χ 1 2 · C 02 - 0.5 · C 01 · χ 1 &dd; χ 1

Вывод результата счета - время достижения &tgr; ⁡ χ и &tgr; 1 ⁡ χ 1 степени превращения оксида азота c при 273 и 323К соответственно в реакции
2 · NO + Cl 2 ===> 2 NOCl
Просмотреть все компоненты c и t(c), которые не помещаются на экране, в частности, те, которые заданы в условии задачи, можно с помощью вертикальной полосы прокрутки.

Рассчитаем (как просили сделать в условии задачи) время достижения степени превращения NO c = 0.8 при температуре 273К.

&tgr; 1 ⁡ 0.8 = 0.024

Ðèñ. 14.6. Çàâèñèìîñòü âðåìåíè äîñòèæåíèÿ ñòåïåíè ïðåâðàùåíèÿ â ðåàêöèè 2 · NO + Cl 2 ===> 2 NOCl: &tgr;. ⁡ χ ïðè 273Ê è &tgr; 1 ⁡ χ ïðè 323Ê.
Начальные концентрации (моль/л) исходных веществ соответственно равны:
оксида азота - 0.02 и молекулярного хлора - 0.035.

Ðèñ. 14.7. Çàâèñèìîñòü âðåìåíè ñòåïåíè ïðåâðàùåíèÿ îò âðåìåíè ïðîâåäåíèÿ ïðîöåññà â ðåàêöèè
2 · NO + Cl 2 ===> 2 NOCl:
&tgr;. ⁡ χ ïðè 273Ê è &tgr; 1 ⁡ χ ïðè 323Ê.
Начальные концентрации (моль/л) исходных веществ соответственно равны:оксида азота - 0.02 и молекулярного хлора - 0.035.

Задача 3.15.
Определите зависимость концентраций от времени в последовательных реакциях второго порядка
2A ----> 2B -----> 2C
k 1 k 2

Решение.
Рассматриваемая задача несколько сложнее, чем рассмотренная в задаче 3. последовательнаая реакция первого порядка A ---> B ---->C.
Запишем кинетические уравнения реакций:

Скорость по веществу А
r A = - &dd; &dd; ⁢ &tgr; ⁢ C A = k 1 · C A 2 (15.1)
Или, введя обозначение C A = C 0

r A = - &dd; &dd; ⁢ &tgr; ⁢ C 0 = k 1 · C 0 2 (15.2)

Скорость по веществу B

r B = &dd; &dd; ⁢ &tgr; ⁢ C B = k 1 · C A 2 - k 2 · C B 2 (15.3)

Или, введя обозначение C B = C 1

r B = &dd; &dd; ⁢ &tgr; ⁢ C 1 = k 1 · C 0 2 - k 2 · C 1 2 (15.4)

Скорость по веществу C

r C = &dd; &dd; ⁢ &tgr; ⁢ C C = k 2 · C B 2 (15.5)
Или, введя обозначение C C = C 2

r C = &dd; &dd; ⁢ &tgr; ⁢ C 2 = k 2 · C 1 2 (15.6)

Система дифференциальных уравнений (15.2), (15.4), (15.6) имеет аналитическое решение, которое, например, в книге " Основы химической кинетики" (Е.Н. Еремин, Москва, Высшая школа, 1976, с.60) занимает четыре страницы.
Инструментарий Mathcad позволяет решить эту систему, используя встроенную функцию rkfixed.

Определение значений констант скоростей
реакций. Вы можете изменить эти значения и проследить, как это скажется на ходе кривых концентрация - время.

k 1 &colon;=&Space; 0.08

k 2 &colon;=&Space; 0.05

Система кинетических уравнений в
дифференциальной форме.

D ⁡ &tgr; C &colon;=&Space; ( - k 1 · C 0 2 k 1 · C 0 2 - k 2 · C 1 2 k 2 · C 1 2 )

C0 &colon;=&Space; ( 0.1 0 0 )

Ввод числа шагов, на которых численный метод находит решение.

M &colon;=&Space; 100

Присваивание матричной переменной u результата действия функции rkfixed.
Параметр t - âðåìÿ - èçìåíÿåòñÿ îò 0 äî 2000.

u &colon;=&Space; rkfixed ⁡ C0 0 2000 M D

Результат решения системы.
Просмотреть все компоненты матрицы, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки.
В матрице u:
u1 - концентрация исходного вещест ва A,
u2 - концентрация промежуточно- го продукта B,
u3 - концентрация продукта реакции C.

Рис. 15.1. Зависимость концентрации
исходного вещества от времени в реакции

2A ===> 2B ===> 2C

Рис. 15.2. Зависимость концентрации про-
промежуточного вещества от времени в
реакции
2A ===> 2B ===> 2C

Рис. 15.3. Зависимость концентрации
продукта реакции от времени в реакции

2A ===> 2B ===> 2C

Сравнительный ход зависимостей концентрации исходного вещества u < 1 > , промежуточного соединения u < 2 > и продукта реакции u < 3 > от времени проведения процесса в реакции
2A ===> 2B ===> 2C
приведен в рис. 15.4.

Рис. 15.4. Зависимость концентрации исходного вещества u < 1 > , промежуточного соединения u < 2 > и продукта реакции u < 3 > от времени проведения процесса в реакции
2A ===> 2B ===> 2C

Задача 3.16
Исследуйте возможеность определения зависимости концентрации и степени превращения c исходного вещества и продукта реакции от времени, а также зависимость времени достижения заданной концентрации (или степени превращения) от концентрации в реакциях вида

aA ---> bB,
если скорость реакции описывается кинетическим уравнением n - го порядка.

Решение.
Для такого типа реакций можно записать кинетические уравнения в дифференциальной форме:
скорость реакции по веществу A

r A = - &dd; &dd; ⁢ &tgr; ⁢ C A = k · C A n (16.1)
или
r A = - &dd; &dd; ⁢ &tgr; ⁢ C 0 = k · C 0 n (16.2)

скорость реакции по веществу B:

r B = &dd; &dd; ⁢ &tgr; ⁢ C B = b a · k · C A n (16.3)
или
r B = &dd; &dd; ⁢ &tgr; ⁢ C 1 = b a · k · C 0 n (16.4)

Для нахождения зависимости концентрации исходного вещества и продукта реакции от времени решим систему дифференциальных уравнений (16.2) - (16.4), используя имеющуюся в Mathcad встроенную функцию rkfixed, которая позволяет решить поставленную задачу методом Рунге - Кутты с фиксированным шагом.
Для конкретизации задачи и наглядности подхода рассмотрим реакцию вида
2A -------> B,

порядок реакции которой по веществу А равен n = 1.5 и константа скорости
k = 0.1. Начальная концентрация вещества А равна 0.5 моль/л
Вы можете исследовать реакцию с другими стехиометрическими коэффициентами, , другими значениями начальной концентрации исходного вещества и продукта реакции и другими значениями константы скорости реакции.

a &colon;=&Space; 2

b &colon;=&Space; 1

n &colon;=&Space; 1.5

Ввод значений стехиометрических коэффи-
циентов, порядка реакции и константы скорости.
Вы можете ввести другие значения, соответствующие другой реакции рассматриваемого типа.

k &colon;=&Space; 0.1

Система кинетических уравнений в дифференциальной форме.

D ⁡ &tgr; C &colon;=&Space; ( - k · C 0 n b a · k · C 0 n )

C0 &colon;=&Space; ( 0.5 0 )

M &colon;=&Space; 100

Ввод числа шагов, на которых численный метод находит решение.

u &colon;=&Space; rkfixed ⁡ C0 0 100 M D

Присваивание матричной переменной u результата действия функции rkfixed.

Результат решения системы.
Просмотреть все компоненты матрицы, которые не помещают- тся на экране, можно с помощью вертикальной полосы прокрутки.
В матрице u:
u1 - концентрация исходного вещест ва A,
u2 - концентрация продукта B,

Рис.16.2. Зависисость концентрации
продукта от времени в реакции

2A ===> B

Рис. 16.1 Зависисость концентрации
исходного вещества от времени в реакции

2A ===> B

Теперь рассмотрим зависимость степени превращения c вещества А от времени.
Кинетическое уравнение в дифференциальной форме зависимости степени превращения от времени для рассмотриваемого типа реакций будет иметь вид:

r A = &dd; &dd; ⁢ &tgr; ⁢ χ = k · C 0 · A · 1 - χ n (16.5)

Для решения дифференциального уравнения (16.5) можно использовать вычислительный блок Given/Odesolve.
Дифференциальное уравнение в этом случае записывается в стандартной, а потому наглядной форме представления задачи.

Ввод значений константы скорости, начальной концентрации и порядка реакции.
Вы можете ввести другие значения, соответствующие другой реакции рассматриваемого типа.

k &colon;=&Space; 0.1

C 0 &colon;=&Space; 0.5

n &colon;=&Space; 2

Ключевое слово.

Given

Дифференциальное уравнение, записанное с помощью логических операторов и начальное условие.
Начальное условие вы можете изменить.

&dd; &dd; ⁢ &tgr; ⁢ χ ⁡ &tgr; = k · C 0 · 1 - χ ⁡ &tgr; n

χ ⁡ 0 = 0

Odesolve(t,t1) - встроенная функция для
решения дифференциального уравнения
первого порядка относительно переменной t на интервале (t0, t1).

χ &colon;=&Space; Odesolve ⁡ &tgr; 100

&tgr; &colon;=&Space; 0 , 1 .. 100

Вывод результата - зависимость степени превращения от времени в исследуемой реакции реакции.

Полученные результаты иллюстрирует рис. 16.3.

Рис.16.3. Зависимость степени превращения
исходного вещества от времени в реакции 2A ===> B

И. наконец, рассмотрим задачу определения времени достижения определенного значения степени превращения c.
В общем виде зависимость времени достижения определенной степени превращения c от степени превращения можно выразить соотношегнием

Тогда для рассматриваемого типа реакций

χ &colon;=&Space; 0 , 0.01 .. 0.99

k &colon;=&Space; 0.1

C 0 &colon;=&Space; 0.5

n &colon;=&Space; 1.5

Ввод соотношения, определяющего зависимость времени достижения степени превращения исходного вещества в реакции
n - го порядка 2A ===> B

Вывод результата - зависимость времени достижения степени превращения исходного вещества в реакции
n - го порядка 2A ===> B

Рис.16.4. Зависимость времени достижения степени превращения исходного вещества от степени превращения в реакции
2A ===> B

Задача 3.17
Исследуйте возможеность определения зависимости концентрации и степени превращения c исходного вещества и продукта реакции от времени, а также зависимость времени достижения заданной концентрации (или степени превращения) от концентрации в обратимых реакциях вида

aA+bB <====> lL+mM,

если скорость реакции описывается кинетическим уравнением n - го порядка.

Решение.
Для такого типа реакций

aA+bB <====> lL+mM

можно записать кинетические уравнения в дифференциальной форме:.

Для реакций с различными стехиометрическими коэффициентами при реагентах скорости изменения концентраций будут разными.

1 l · &dd; &dd; ⁢ &tgr; ⁢ � L = 1 m · &dd; &dd; ⁢ &tgr; ⁢ � M = - 1 b · &dd; &dd; ⁢ &tgr; ⁢ � B = - 1 a · &dd; &dd; ⁢ &tgr; ⁢ � A

Выразим концентрации веществ в момент времени t относительно концентрации, например, вещества A:

aA + bB <====> lL + mM

Èñõîäíàÿ êîíöåíòðàöèÿ, A B L M
ìîëü/ë

ïðîðåàãèðîâàëî ê A - C(t) b a · A - C ⁡ &tgr; l a · A - C ⁡ &tgr; m a · A - C ⁡ &tgr;
ìîìåíòó t

êîíöåíòðàöèÿ
â ìîìåíò t C(t) B - b a · A - C ⁡ &tgr; L + l a · A - C ⁡ &tgr; M + m a · A - C ⁡ &tgr;

Запишем кинетическое уравнение по веществу А

&dd; &dd; ⁢ &tgr; ⁢ C ⁡ &tgr; = - k 1 · C ⁡ &tgr; n · B - b a · A - C ⁡ &tgr; j + k 2 · L + l a · A - C ⁡ &tgr; g · M + m a · A - C ⁡ &tgr; s , (17.1)

где k 1 , k 2 - константы скорости прямого и обратного процессов при температуре
Т и A, B, L, M - начальные концентрации реагирующих веществ и продуктов
реакции, a, b, l, m - стехиометрические коэффициенты и n, j, g, s - порядки
реакции по веществам соответственно.

Для конкретики рассмотрим обратимую реакцию

2HJ <====> H2 +J2

для которой известны значени константы скорости прямой реакции и константа равновесия K при различных температурах (а, значит, и константа скорости обратного процесса), поскольку
k 1 k 2 = K

( � ⁡ � k 1 K 781 0.0395 0.029 700 0.00310 0.018 666 0.000588 0.015 629 0.0000809 0.012 556 0.000000942 0.0079 ) ,

размерность константы скорости ( � · �� - 1 · � - 1 )

Для решения дифференциального уравнения (17.1)

&dd; &dd; ⁢ &tgr; ⁢ C ⁡ &tgr; = - k 1 · C ⁡ &tgr; n · B - b a · A - C ⁡ &tgr; j + k 2 · L + l a · A - C ⁡ &tgr; g · M + m a · A - C ⁡ &tgr; s

используем вычислительный блок Given/Odesolve.
Дифференциальное уравнение в этом случае записывается в стандартной, а потому наглядной форме представления задачи.

Ввод значений стехиометрических коэффициентов

a &colon;=&Space; 2

b &colon;=&Space; 0

l &colon;=&Space; 1

m &colon;=&Space; 1

n &colon;=&Space; 2

j &colon;=&Space; 0

g &colon;=&Space; 1

s &colon;=&Space; 1

Ввод значений порядков реакций по
веществам.

A &colon;=&Space; 1

B &colon;=&Space; 0

L &colon;=&Space; 0

M &colon;=&Space; 0

Ввод значений начальных концентраций
веществ

Ввод значений констант скоростей прямой k 1 и обратной k 2 реакции при Т= 781К

k 1 &colon;=&Space; 0.0395

k 2 &colon;=&Space; 1.362

Вы можете ввести другие значения, соответствующие другой реакции рассматриваемого типа.

Given

Ключевое слово.

&dd; &dd; ⁢ &tgr; ⁢ C ⁡ &tgr; = - k 1 · C ⁡ &tgr; n · B - b a · A - C ⁡ &tgr; j + k 2 · L + l a · A - C ⁡ &tgr; g · M + m a · A - C ⁡ &tgr; s

C ⁡ 0 = 1.0

Дифференциальное уравнение обратимой реакции, записанное с помощью логических операторов и начальное условие.
Начальное условие вы можете изменить.

Odesolve(t,t1) - встроенная функция для решения дифференциального уравнения первого порядка относительно переменной t на интервале (t0, t1).

C &colon;=&Space; Odesolve ⁡ &tgr; 200

&tgr; &colon;=&Space; 0 , 1 .. 200

Вывод результата - зависимость концентрации иодистого водорода от времени проведения процесса в обратимой реакции
2HJ <====> H2 +J2
ïðè 781Ê.

Результат при дргом значении времени может быть получен обычными средствами Mathcad для определения значения функции в какой-либо точке, напрмер, C ⁡ 40 = 0.746

Полученные результаты иллюстрирует рис. 17.1

Рис. 17.1. Зависимость концентрации исходного вещества от времени при проведении процесса
2HI <===> H2 + I2
при температуре 781К.

Концентрация продукта реакции C 1 ⁡ &tgr; связана с концентрацией исходного вещества соотношением
C 1 ⁡ &tgr; = L + l a · A - C ⁡ &tgr; , (17.2)
которое позволяет при подстановке в (17.2) значения С(t) рассчитать концентрацию продукта во времени.

C 1 ⁡ &tgr; &colon;=&Space; L + l a · A - C ⁡ &tgr;

Ввод соотношения, определяющего концентрацию продукта реакции от времени

Вывод результата - зависимость концентрации продукта реакции от времени проведения процесса в обратимой реакции
2HJ <====> H2 +J2
ïðè 781Ê.

Построим график зависимости концентраций исходного вещества HJ C ⁡ &tgr; и продукта реакции H 2 C 1 ⁡ &tgr; от времени при 781К.

Обратите внимание на ход
зависимостей:такое изменение
концентраций характерно при
соотношении констант скоростей
прямого и обратного процессов
K = k 1 k 2 <1

Рис. 17.2. Зависимость концентрации исходного
вещества С(t) и продукта реакции C 1 ⁡ &tgr; от времени при проведении процесса
2HI <===> H2 + I2
при температуре 781К.

a &colon;=&Space; 2

b &colon;=&Space; 0

l &colon;=&Space; 1

m &colon;=&Space; 1

n &colon;=&Space; 2

j &colon;=&Space; 0

g &colon;=&Space; 1

s &colon;=&Space; 1

A &colon;=&Space; 1

B &colon;=&Space; 0

L &colon;=&Space; 0

M &colon;=&Space; 0

k 11 &colon;=&Space; 3.10 · 10 - 3

Ввод значений константы скорости прямой реакции k 11 и константы равновесия реакции K 1 при Т= 700К

K 1 &colon;=&Space; 0.018

Ввод значения константы скорости обратной k 21 реакции при Т= 700К

k 21 &colon;=&Space; k 11 K 1

k 21 = 0.172

Given

&dd; &dd; ⁢ &tgr; ⁢ c ⁡ &tgr; = - k 11 · c ⁡ &tgr; n · B - b a · A - c ⁡ &tgr; j + k 21 · L + l a · A - c ⁡ &tgr; g · M + m a · A - c ⁡ &tgr; s

c ⁡ 0 = 1.0

Odesolve(t,t1) - встроенная функция для решения дифференциального уравнения первого порядка относительно переменной t на интервале (t0, t1).

c &colon;=&Space; Odesolve ⁡ &tgr; 200

&tgr; &colon;=&Space; 0 , 1 .. 200

Вывод результата - зависимость концентрации иодистого водорода от времени проведения процесса в обратимой реакции
2HJ <====> H2 +J2
ïðè 700Ê.

Результат при дргом значении времени может быть получен обычными средствами Mathcad для определения значения функции в какой-либо точке, напрмер, c ⁡ 40 = 0.896

� 1 ⁡ &tgr; &colon;=&Space; L + l a · A - c ⁡ &tgr;

Ввод соотношения, определяющего концентрацию продукта реакции от времени

Вывод результата - зависимость концентрации продукта реакции от времени проведения процесса в обратимой реакции
2HJ <====> H2 +J2
ïðè 700Ê.

Построим график зависимости концентраций исходного вещества HJ � ⁡ &tgr; и продукта реакции H 2 � 1 ⁡ &tgr; от времени при 700К.

Обратите внимание на ход зависимостей:
такое изменение концентраций характерно при соотношении констант скоростей прямого и обратного процессов
K = k 1 k 2 <1

Рис. 17.3. Зависимость концентрации исходного вещества c. ⁡ &tgr; и продукта реакции c 1 ⁡ &tgr; от времени при проведении процесса
2HI <===> H2 + I2
при температуре 700К.

Сравнение зависимостей концентраций исходного вещества и продукта реакции при 700К и и 781К от времени проведении процесса
2HI <===> H2 + I2
приведено на рис. 17.4.

Рис. 17.4. Зависимость концентрации исходного вещества c. ⁡ &tgr; и продукта реакции c 1 ⁡ &tgr; при 700К и C ⁡ &tgr; и C 1 ⁡ &tgr; при 781К от времени проведения процесса
2HI <===> H2 + I2

Задача 3.18
Рассмотрим более сложный случай обратимых реакций - например, реакцию окисления оксида азота

2NO + O 2 <====> 2N O 2 ,
которая имеет третий порядок в прямом и второй порядок в обратном направлениях.
Исследуйте зависимости концентраций исходных веществ и продуктов реакцмм от времени проведения процесса.

Решение.
Из-за сложности получаемых аналитических выражений кинетические уравнения в интегральной форме мало удобны для практического применения и в этом случае применение инструментария Mathcad особенно целесообразно.
Для общего случая реакций вида

aA+bB <====> lL+mM

выразим концентрации веществ в момент времени t относительно концентрации, например, вещества A:

aA + bB <====> lL + mM

Èñõîäíàÿ êîíöåíòðàöèÿ, A B L M
ìîëü/ë

ïðîðåàãèðîâàëî ê A - C(t) b a · A - C ⁡ &tgr; l a · A - C ⁡ &tgr; m a · A - C ⁡ &tgr;
ìîìåíòó t

êîíöåíòðàöèÿ
â ìîìåíò t C(t) B - b a · A - C ⁡ &tgr; L + l a · A - C ⁡ &tgr; M + m a · A - C ⁡ &tgr;

и запишем кинетическое уравнение по веществу А

&dd; &dd; ⁢ &tgr; ⁢ C ⁡ &tgr; = - k 1 · C ⁡ &tgr; n · B - b a · A - C ⁡ &tgr; j + k 2 · L + l a · A - C ⁡ &tgr; g · M + m a · A - C ⁡ &tgr; s

где k 1 , k 2 - константы скорости прямого и обратного процессов при температуре Т и A, B, L, M - начальные концентрации реагирующих веществ и продуктов реакции, a, b, l, m - стехиометрические коэффициенты и n, j, g, s - порядки реакции по веществам соответственно.
Тогда для исследуемой реакции

2NO + O 2 <===> 2N O 2

Ввод стехиометричесих коэффициентов

a &colon;=&Space; 2

b &colon;=&Space; 1

l &colon;=&Space; 2

m &colon;=&Space; 0

Ввод начальных концентраций реагентов

B &colon;=&Space; 1

L &colon;=&Space; 0

M &colon;=&Space; 0

Ввод значений порядка реакций по веществам

n &colon;=&Space; 2

j &colon;=&Space; 1

g &colon;=&Space; 2

s &colon;=&Space; 0

k 1 &colon;=&Space; 0.8

k 2 &colon;=&Space; 0.5

Ввод констант скоростей прямой k 1 и обратной k 2 реакций.

Given

Ввод ключевого слова

&dd; &dd; ⁢ &tgr; ⁢ C ⁡ &tgr; = - k 1 · C ⁡ &tgr; n · B - b a · A - C ⁡ &tgr; j + k 2 · L + l a · A - C ⁡ &tgr; g · M + m a · A - C ⁡ &tgr; s

Дифференциальное уравнение, записанное с помощью логических операторов и начальное условие.
Начальное условие вы можете изменить.

C ⁡ 0 = 1

Odesolve(t,t1) - встроенная функция для решения дифференциального уравнения первого порядка относительно переменной t на интервале (t0, t1).

C &colon;=&Space; Odesolve ⁡ &tgr; 250

Концентрация продукта реакции C 1 ⁡ &tgr; связана с концентрацией исходного вещества в реации
2NO + O 2 <===> 2N O 2
соотношением

C 1 ⁡ &tgr; = L + l a · A - C ⁡ &tgr; , (18.2)
которое позволяет при подстановке в (18.2) значения С(t) рассчитать концентрацию продукта во времени.

Ввод соотношения, определяющего концентрацию продукта реакции от времени проведения процесса.

C 1 ⁡ &tgr; &colon;=&Space; L + l a · A - C ⁡ &tgr;

&tgr; &colon;=&Space; 0 , 1 .. 200

Вывод результата - зависимость концентрации оксида азота � ⁡ &tgr; и продукта реакции дтоксида азота C 1 ⁡ &tgr; от времени проведения процесса
2NO + O 2 <===> 2N O 2

Полученные результаты иллюстрирует рис. 18.1

Обратите внимание на ход зависимостей:
такое изменение концентраций характерно при соотношении констант скоростей прямого и обратного процессов
K = k 1 k 2 >1

Рис. 18.1. Зависимость концентрации исходного вещества С(t) и продукта реакции C 1 ⁡ &tgr; от времени при проведении процесса
2NO + O 2 <====> 2N O 2
Значения константа скорости прямой k 1 = 0.8 и обратной k 2 = 0.5 реакций.

Задача 3.19.

Для обратимой реакции первого порядка

A <===>B

изменение энтальпии при 298К ΔH 0 298 = - 60 · 10 3 · �� .
Константа равновесия K c 298 = 5.5 .
Зависимость константы скорости прямой реакции от температуры описывается соотношением

k 1 ⁡ T = 3.8 · 10 5 · e - 45800 R · T , � - 1
Начальная концентрация вещества A C 0 = 2 · �� . Продукт реакции В в начальный момент отсутствует.
При различном времени протекания реакции определите температуру Т, при которой степень превращения исходного вещества c максимальна.

Решение.

Если обратимая реакция эндотермична, т.е. протекает с поглащением тепла, то и константа равновесия K c такой реакции в соответствии с изобарой Вант-Гоффа

&dd; &dd; ⁢ T ⁢ ln ⁡ K c = ΔH R · T 2
и константа скорости реакции в соответствии с уравнением Аррениуса

k. ⁡ T = k 0 · e - E a R · T
с возрастанием температуры увеличиваются. В этом случае повышение температуры благоприятно сказывается на сдвиг равновесия в сторону продуктов реакции и скорость процесса.
При экзотермической реакции влияние температуры на константу равновесия и константу скорости противоположно: константа скорости с увеличением температуры увеличивается, а константа скорости - уменьшается.
Поэтому возникает задача поиска оптимальной температуры, при которой степень превращения была бы максимальна.
Поскольку рассматриваемая реакция - обратимая реакция первого порядка, то ее кинетическое уравнение

- &dd; &dd; ⁢ &tgr; ⁢ C A = k 1 · C A - k 2 · C B ,

где k 1 и k 2 - константы скорости прямой k 1 и обратной k 2 реакции.
В соответствии с соотношением

C A = C 0 · 1 - χ ,

связывающим текущую концентрацию C A вещества А с его начальной концентрацией C 0 и степенью превращения c, уравнение
- &dd; &dd; ⁢ &tgr; ⁢ C A = k 1 · C A - k 2 · C B
можно записать как
&dd; &dd; ⁢ &tgr; ⁢ C 0 · 1 - χ = k 1 · C 0 · 1 - χ - k 2 · C 0 · χ

После несложных преобразований получим:

&dd; &dd; ⁢ &tgr; ⁢ χ = k 1 - k 1 + k 2 · χ
Для обратимых реакций константы скорости прямой k 1 и обратной k 2 реакции связаны с константой равновесия соотношением

k 1 k 2 = K
Подставим в предыдущее уравнение:

&dd; &dd; ⁢ &tgr; ⁢ χ = k 1 - k 1 + k 1 K · χ

и после упрощений получим

&dd; &dd; ⁢ &tgr; ⁢ χ = k 1 · 1 - 1 + 1 K · χ

По условию задачи константа скорости прямой реакции зависит от температуры
k 1 ⁡ T = 3.8 · 10 5 · e - 45800 R · T

Зависимость константы равновесия от температуры (в приближении, что в области температур 298 -Т темепература не влияет на изменение энтальпии реакции и выражается уравнением):

K c ⁡ T = K c 298 · e ΔH 298 R · 1 298 - 1 T

Следовательно, задача сводится к расчету константы равновесия К и константы скорости прямой реакции k 1 при различных температурах, подстановке их значений в дифференциальное уравнение

&dd; &dd; ⁢ &tgr; ⁢ χ = k 1 · 1 - 1 + 1 K · χ

и его решению.
Ниже проедставлены результаты решения (с помощью встроенной функции Odesolve, имеющейся в математическом пакете MathCAD) при трех температурах и графическая иллюстрация полученных результатов.

k 0 &colon;=&Space; 3.8 · 10 5

E a &colon;=&Space; 45800

Ввод предхэкспоненциального множителя и энергии активации прямой реакции.

Ввод значения изменения энтальпии реакции (Дж/моль) и константы равновесия при 298К (Дж/моль).

ΔH &colon;=&Space; - 60 · 10 3

K C &colon;=&Space; 5.5

T &colon;=&Space; 298

C 0 &colon;=&Space; 2

Ввод начальной концентрации (моль/л) и значения температуры.

R &colon;=&Space; 8.31

Ввод соотношения, определяющего зависимость константы равновесия прямой реакции от температуры.

k 1 ⁡ T &colon;=&Space; k 0 · e - E a R · T

Ââîä ñîîòíîøåíèÿ, îïðåäåëÿþùåãî ñâÿçü ìåæäó êîíñòàíòàìè ðàâíîâåñèÿ ïðÿìîé è îáðàòíîé ðåàêöèè

K ⁡ T &colon;=&Space; k 1 ⁡ T k 2 ⁡ T

Ввод соотношения, определяющего связь константы равновесия исследуемой реакции и температурой.

K ⁡ T &colon;=&Space; K C · e ΔH R · 1 298 - 1 T

Ввод ключевого слова.

Given

Ввод кинетического уравнения в дифференциальной форме, определяющего связь между степенью превращения исходного вещества и временем проведения процесса.

&dd; &dd; ⁢ &tgr; ⁢ χ ⁡ &tgr; = k 1 ⁡ T · 1 - 1 + 1 K ⁡ T · χ ⁡ &tgr;

χ ⁡ 0 = 0

Ввод начального условия.

χ &colon;=&Space; Odesolve ⁡ &tgr; 1000

&tgr; &colon;=&Space; 0 , 50 .. 1000

Вывод результата - степень превращения исходного вещества от времени проведения обратимой реакции реакции
A <===>B
при 298К.

Проведем теперь расчет при 315К.

Ввод температуры.

T &colon;=&Space; 315

Given

Ввод кинетического уравнения в дифференциальной форме, определяющего связь между степенью превращения исходного вещества и временем проведения обратимой реакции реакции
A <===>B
при температуре Т.

&dd; &dd; ⁢ &tgr; ⁢ χ 1 ⁡ &tgr; = k 0 · e - E a R · T · 1 - 1 + 1 K C · e ΔH R · 1 298 - 1 T · χ 1 ⁡ &tgr;

χ 1 ⁡ 0 = 0

Ввод начального условия

χ 1 &colon;=&Space; Odesolve ⁡ &tgr; 1000

Вывод результата - степень превращения исходного вещества от времени проведения обратимой реакции реакции
A <===>B
при 315К.

Проведем теперь расчет при 330К.

T &colon;=&Space; 330

Given

&dd; &dd; ⁢ &tgr; ⁢ χ 2 ⁡ &tgr; = k 0 · e - E a R · T · 1 - 1 + 1 K C · e ΔH R · 1 298 - 1 T · χ 2 ⁡ &tgr;

χ 2 ⁡ 0 = 0

Ввод начального условия

χ 2 &colon;=&Space; Odesolve ⁡ &tgr; 1000

&tgr; &colon;=&Space; 0 , 5 .. 1000

Вывод результата - степень превращения исходного вещества от времени проведения обратимой реакции реакции
A <===>B
при 330К.

Рис. 19.1 Зависимость степени превращения исходного вещества от времени проведения обратимой реакции реакции
A <===>B
при различных температурах.
χ 1 - 298К, χ 2 - 315К и χ 3 - 330К.

Задача 3.20.
При исследовании кинетики реакции термического разложения ацетальдегида CH 3 · CHO было показано, что скорость образования метана при 673К описывается кинетическим уравнением
r CH4 = 4 · 10 - 3 · C CH3CHO 3 2 , �� · �
Исследователи предположили следующий механизм реакции:

Инциирование: CH 3 · CHO --- k 1 -----> CH 3 + CHO

CH 3 + CH 3 · CHO --- k 2 --> CH 4 + CH 2 · CHO

Продолжение цепи: CH 2 · CHO --- k 3 ----> CH 3 + CO
CH 3 + CH 3 · CHO --- k 4 ---> CH 4 + CH 2 · CHO
Обрыв цепи: 2 · CH 3 -------> C 2 · H 6

Покажите, удовлетворяет ли предложенная схема реакции кинетическому уравнению, полученному в эксперименте.
Предложите - на основании приведенного механизма процесса - кинетические уравнения по ацетальдегиду r CH3CHO и оксиду углерода r CO .
Решение.

При анализе схем многостадийных реакций, на определенных стадиях которых образуются промежуточные соединения с высокой реакционной способностью, особенно полезен метод стационарных концентраций,
Условием применимости метода является малое время жизни промежуточных соединений по сравнению с временем, за которое состав реакционной системы успевает значительно измениться. Аналитически это означает, что сорость по этим веществам принимается равной нулю.
Тогда для исследуемой реакции скорость по метану

r CH4 = &dd; &dd; ⁢ &tgr; ⁢ C CH4 = k 2 · C CH3 · C CH3CHO (20.1)

скорость по оксиду углерода

r CO = &dd; &dd; ⁢ &tgr; ⁢ C CO = k 3 · C CH2CHO (20.2)
скорость по ацетальдегиду

r CH3CHO = &dd; &dd; ⁢ &tgr; ⁢ C CH3CHO = - k 1 · C CH3CHO - k 2 · C CH3CHO · C CH3 (20.3)

и скорость по бензолу

r C2H6 = &dd; &dd; ⁢ &tgr; ⁢ C C2H6 = k 4 · C CH3 2 (20.4)

Во все приведенные уравнения входят концентрации нестойких промежуточных соединений CH3 и CH2CHO .
Воспользуемся методом стационарных концентраций и запишем кинетические уравнения для промежуточных соединений.

&dd; &dd; ⁢ &tgr; ⁢ C CH3 = k 1 · C CH3CHO - k 2 · C CH3 · C CH3CHO + k 3 · C CH2CHO - 2 · k 4 · C CH3 2 = 0 (20.5)

&dd; &dd; ⁢ &tgr; ⁢ C CH2CHO = k 2 · C CH3 · C CH3CHO - k 3 · C CH2CHO = 0 (20.6)

Решим с помощью символьного редактора Mathcad эту систему уравнений относительно концентраций промежуточных соединений CH3 и CH2CHO .
Из уравнения (20.6) следует, что

C CH2CHO = k 2 · C CH3 · C CH3CHO k 3 (20.7)
Подставим полученное соотношение в уравнение (20.5)

k 1 · C CH3CHO - k 2 · C CH3 · C CH3CHO + k 3 · C CH2CHO - 2 · k 4 · C CH3 2 = 0
и тогда получим
k 1 · C CH3CHO - k 2 · C CH3 · C CH3CHO + k 3 · k 2 · C CH3 · C CH3CHO k 3 - 2 · k 4 · C CH3 2 = 0 (20.8),

которое решим, используя символьный редактор Mathcad

C CH3 = 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2

20.9

Подставим полученное выражение в уравнение (20.7)

C CH2CHO = k 2 · C CH3 · C CH3CHO k 3
и определим концетрацию промежуточного соединения .CH2CHO :

C CH2CHO = k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO k 3 (20.10)

Теперь, подставив полученные выражения концентрации промежуточных соединений в уравнение (20.1)

r CH4 = &dd; &dd; ⁢ &tgr; ⁢ C CH4 = k 2 · C CH3 · C CH3CHO
определим зависимость скорости реакции по метану от концентрации ацетальдегида:
r CH4 = k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO , (20.11)
которое полностью совпадает с полученным в результате эксперимента (20.1):
r CH4 = 4 · 10 - 3 · C CH3CHO 3 2 (20.1)

Аналогичным образом определим скорость реакции по оксиду углерода,
подставив в уравнение (20.2):
r CO = &dd; &dd; ⁢ &tgr; ⁢ C CO = k 3 · C CH2CHO
концентрацию промежуточного соединения CH2CHO (20.10)

C CH2CHO = k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO k 3

Тогда получим

r CO = k 3 · k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO k 3 (20.12)

И скорость реакции по ацетальдегиду:

r CH3CHO = &dd; &dd; ⁢ &tgr; ⁢ C CH3CHO = - k 1 · C CH3CHO - k 2 · C CH3CHO · C CH3 (20.3)
после подстановки в (20.3) концентрации C CH3 (20.9) :
C CH3 = 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2

получим ктнеическое уравнение r CH3CHO = &dd; &dd; ⁢ &tgr; ⁢ C CH3CHO = - k 1 · C CH3CHO - k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO (20.13)

Обратите внимание на полученный результат: скорости накопления или распада стабильных участников реакции зависят только от текущей концентрации ацетальдегида.
Таким образом, получена система дифференциальных уравнений:

&dd; &dd; ⁢ &tgr; ⁢ C CH3CHO = - k 1 · C CH3CHO - k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO

&dd; &dd; ⁢ &tgr; ⁢ C CO = k 3 · k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO k 3

&dd; &dd; ⁢ &tgr; ⁢ C CH4 = k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C CH3CHO 1 2 · C CH3CHO

&dd; &dd; ⁢ &tgr; ⁢ C C2H6 = 1 2 · k 1 · C CH3CHO

Введем обозначения: C CH3CHO = C 0 , C CH4 = C 1 , C CO = C 2 и C C2H6 = C 3 .

k 1 &colon;=&Space; 10 - 7

k 2 &colon;=&Space; 2.5 · 10 5

Ввод значений констант скоростей при 673К

k 3 &colon;=&Space; 2.5 · 10 6

k 4 &colon;=&Space; 2 · 10 10

Ввод системы кинетических уравнений в дифференциаоьной форме.

D ⁡ &tgr; C &colon;=&Space; ( - k 1 · C 0 - k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C 0 1 2 · C 0 k 3 · k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C 0 1 2 · C 0 k 3 k 2 · 1 2 · k 4 · 2 1 2 · k 4 · k 1 · C 0 1 2 · C 0 1 2 · k 1 · C 0 )

Ввод начальных условий.

C0 &colon;=&Space; ( 0.5 0 0 0 )

Ввод числа шагов, на которых находится решение системы дифференциальных уравненеий.

M &colon;=&Space; 1000

u &colon;=&Space; rkfixed ⁡ C0 0 15000 M D

Âûâîä ðåçóëüòàòà - çàâèñèìîñòü êîíöåíòðàöèé
ó÷àñòíèêîâ ðåàêöèè òåðìè÷åñêîãî ðàçëîæåíèÿ
àöåòàëüäåãèäà îò âðåìåíè ïðîâåäåíèÿ ïðîöåññà
ïðè 673Ê.
В матрице u:
u1 - концентрация исходного вещества ацетальдегида,
u2 - концентрация продукта реакции - метана,
u3 - концентрация продукта реации - оксида углерода,
u2 - концентрация продукта реакции - бензола.
Просмотреть все компоненты матрицы, которые не
помещаюттся на экране, можно с помощью вертикальной
полосы прокрутки.

Рис 20.1 Зàâèñèìîñòü êîíöåíòðàöèé ó÷àñòíèêîâ ðåàêöèè òåðìè÷åñêîãî ðàçëîæåíèÿ
àöåòàëüäåãèäà îò âðåìåíè ïðîâåäåíèÿ ïðîöåññà ïðè 673Ê.
u < 0 > âðåìÿ, ñ.
u < 1 > - концентрация исходного вещества ацетальдегида,
u < 2 > - концентрация продукта реакции - метана,
u < 3 > - концентрация продукта реации - оксида углерода,
u < 4 > - концентрация продукта реакции - бензола.