Валерий
Очков
(http://twt.mpei.ac.ru/ochkov)
Теперь никого не удивляет цвет на экране
дисплея и не бумаге принтера. Дети, да и многие взрослые, рисуя мышкой или просто
играя на компьютере, не могут представить себе, что были времена, когда цвет
воспринимался как чудо. Цвет – это атрибут не только «рисовалок» и игр, но
более серьезных программ. Игры играми, но нужно решать школьные, институтские и
производственные задачи на компьютере. Поговорим о цвете в программах и в
математических пакетах, которые используются для решения таких задач…
Рис. 1. «Цветное» решение задачи в
среде Mathcad
Рис. 2. Программа «Золотое сечение»
Рис. 3. Программа «Золотое сечение»
в рамках структурной диаграммы
Рис. 4. Программа «Золотое сечение» с
«цветной» структурой алгоритма
Рис. 5. Mathcad-программа «Золотое
сечение» с «цветной» структурой данных
Рис. 6. Программа работы с римскими
числами
Рис. 7. Цвет в символьной математике
Mathcad
Новые примера использования цвета в
Mathcad-документах:
Одинаковый цвет переменных и осей
графика
Цвет переменный соответствует ее
названию
Трудно сказать, что
появилось раньше цветные дисплеи и принтеры или потребность в них
(старый спор о том, «что появилось раньше курица или яйцо»). Однозначно
утверждать можно лишь то, что в настоящее время мы не мыслим себе работу на
компьютере без цвета. Здесь можно отметить три функции цвета:
- утилитарная функция
- эстетическая функция
- пустая функция (надо же
чем-то загрузить цветную периферию компьютера).
Цвет особо «буйно расцвел» с появлением программных
средств графического отображения результатов расчетов[1].
На рис. 1 в качестве типичного «цветного»
примера показан Mathcad-документ с решением задачи об остатке жидкости в
горизонтальной цилиндрической цистерне с торцами в виде полусфер[2].
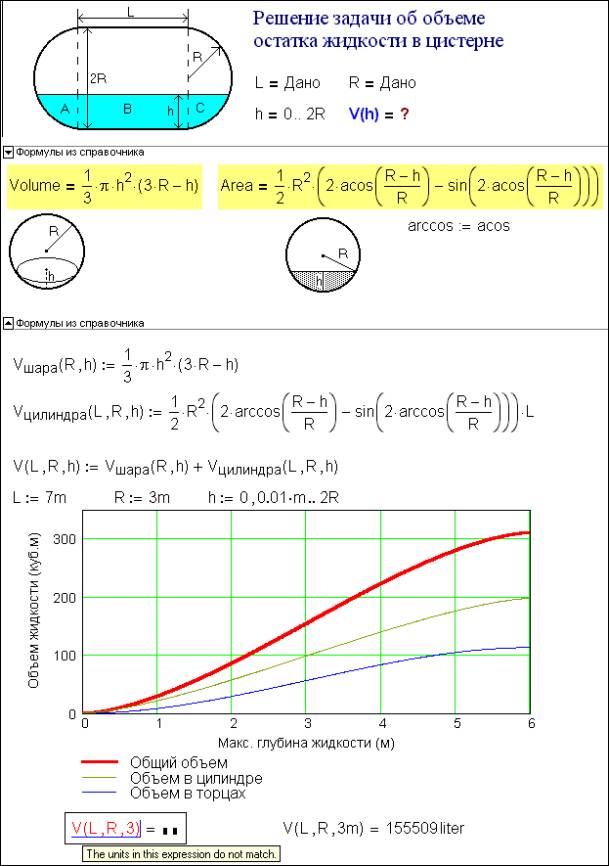
Рис. 1. «Цветное» решение задачи в среде Mathcad
На рис. 1 построен
график зависимости объема остатка жидкости (нефти в железнодорожной цистерне,
например) от ее максимальной глубины[3]
(h). Суть задачи и ход ее решения, автор надеется,
читателю из рис. 1 ясен[4].
Поговорим о цвете.
По умолчанию пользователь
пишет в Mathcad-документе математические выражения черным по
белому, а комментарии к ним – синим по белому. Что в этом «цветоделении»
доминирует – эстетика или утилитарность, сказать трудно. Но отличия в цвете
сопровождаются и отличиями в шрифте (Arial – математические выражения
и Times – комментарии к ним). Это позволяет пользователю Mathcad
понимать «что есть что», работая и с черно-белой периферией (дисплей-принтер).
Это «сине-черно-белое» умолчание можно нарушить, изменив, например, цвет подложки
(background) формул: некоторые математические выражения можно
подсветить («подцветить») для того, чтобы обратить на них внимание будущих
читателей (пользователей) документа. Так на рис. 1
формулы, взятые из справочника[5],
имеют желтый фон[6]. На графике
решения задачи приведены три кривые, отличающиеся друг от друга цветом. При
желании можно поменять не только цвет кривых, но и цвет осей графика и его
сетки, подложки и др. Но главное здесь не переборщить[7]
– думать больше не об эстетике (часто довольно сомнительной), а об
удобочитаемости (утилитарности) графиков и всего Mathcad-документа в целом. Это как
раз тот случай, когда к решению чисто математической задачи можно и нужно
привлечь художника: законченное решение должно быть не только
правильным, но и красивым. В конце рис. 1
рассчитан объем жидкости в цистерне при заданных конкретных значениях
переменных L, R и h.
Вернее сделаны две попытки расчета – неудачная и удачная. В первом случае
выражение V(L, R, 3) = ■ ■ «покраснело» из-за того,
что тройка не была дополнена единицей измерения длины – красный цвет тут имеет
чисто утилитарную функцию обращать внимание пользователя на допущенную ошибку.
Если к «покрасневшей» формуле подвести курсор, то появится («выпадет») сообщение
об ошибке «Несовместимые единицы измерения[8]»:
все аргументы функции V должны быть одной
размерности длины[9].
Цвет присутствует и в рисунке,
поясняющем суть задачи[10].
Рисунок был создан в среде графического редактора PaintBrush[11], а затем перенесен в среду Mathcad.
Если по рисунку цистерны дважды «кликнуть» левой кнопкой мыши, то на экране
дисплея инструменты Mathcad будут заменены на инструменты PaintBrush,
что позволит подправить и/или дополнить рисунок. Это очень удобная технология
внедрения одного приложения Windows в другое[12].
Но оставим в стороне
эстетическую сторону цвета на экране дисплея и на бумаге принтера. Этот сабж[13]
ближе к сфере искусства, чем к сфере компьютерных технологий. Поговорим лучше
об утилитарной, т.е. практической стороне цвета и не просто на экране дисплея
(здесь более-менее все ясно), а в программах.
' Программа поиска минимума функции Y(X) методом золотого сечения
Input "A, B,
TOL"; A, B, TOL
X1 = GP(A, B): Y1 = Y(X1)
X2 = GP(B, A): Y2 = Y(X2)
Do While Abs(A - B) > TOL
If Y1 < Y2 Then
B = X2: X2 = X1: Y2 = Y1: X1 = GP(A, B): Y1 = Y(X1)
Else
A = X1: X1 = X2: Y1 = Y2: X2 = GP(B, A): Y2 = Y(X2)
End If
Loop
X = (A + B) / 2
Print "Ymin = "; Y(X); "at X ="; X
End
Function Y(X)
Y = X ^ 2 + X – 3
End Function
Function
GP(A, B): GP = 3 * B / 2 - A / 2 + SQR(5) * (A - B) / 2
End Function
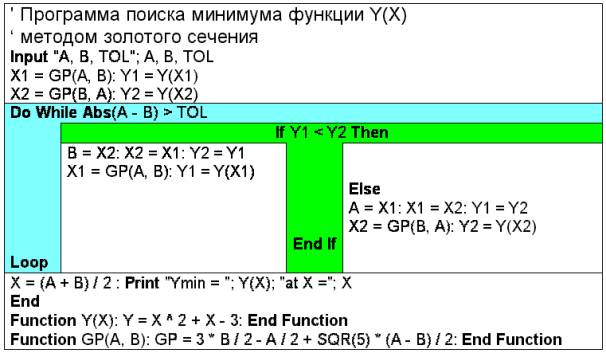
Рис. 2. Программа «Золотое сечение»
На рис. 2 показана программа поиска минимума
методом золотого сечения[14],
написанная на языке BASIC. Редактор этого языка (его популярная версия – Visual Basic, например) сам раскрашивает вводимую программистом
программу в три цвета:
- синий цвет – встроенные
конструкции языка программирования: функции (Abs, например), операторы
(Input, Print) и ключевые слова (Do,
While, If
и т.д.);
- черный цвет –
конструкции программиста – переменные (А, В и т.д.), функции (GP, Y)
·
зеленый
цвет – комментарии, которые можно сравнить с ремарками в тексте пьесы: действующие
лица их не произносят, но они помогают лучше понять мысли автора; комментарии в
тексте программы компьютером (компилятором языка программирования) не
выполняются, но они «помогают лучше понять мысли автора» программы
Рис. 3. Программа «Золотое сечение» в рамках структурной диаграммы
Впервые цвет появился в
языке программирования Quick Pascal.
Но сама идея цвета в программах витала давно. Автор данной статьи, например,
для обучения студентов структурному программированию уже лет двадцать вписывает
программы в рамки структурной диаграммы (см. рис.
3), поля которой заливаются такими цветами:
- синий – цикл с
предпроверкой (сначала проверяю, а потом выполняю)
- зеленый – выбор
(альтернатива)
- красный – цикл с параметром
·
желтый
– цикл с постпроверкой (сначала выполняю, а потом проверяю) и др.
Из структурной диаграммы BASIC-программу
можно изъять и вставить программу, написанную на любом другом языке
программирования (на языке микрокалькулятора, например). Можно просто вставить
в структурную диаграмму словесное описание алгоритма.
' Программа поиска минимума функции Y(X) методом
золотого сечения
Input "A, B, TOL";
A, B, TOL
X1 = GP(A, B): Y1 = Y(X1)
X2 = GP(B, A): Y2 = Y(X2)
Do While Abs(A
- B) > TOL
If Y1
< Y2 Then
B = X2: X2 = X1:
Y2 = Y1: X1 = GP(A, B): Y1 = Y(X1)
Else
A = X1: X1 = X2:
Y1 = Y2: X2 = GP(B, A): Y2 = Y(X2)
End If
Loop
X = (A + B) / 2
Print "Ymin = ";
Y(X); "at X ="; X
End
Function Y(X)
Y = X ^ 2 + X – 3
End Function
Function GP(A, B)
GP = 3 * B / 2 - A / 2 +
SQR(5) * (A - B) / 2
End Function
Рис. 4. Программа «Золотое сечение» с «цветной» структурой алгоритма
На рис. 4 та же программа переписана (расцвечена) так,
что цветом отмечены операторы и ключевые слова, отвечающие за ветвления и циклы
в алгоритме решения задачи.
Идею цвета в программах,
отображенную на рис. 3 и рис. 4, автор задолго до появления у нас цветных
дисплеев[15] оформил в
1987 году в виде статьи, которую отослал в журнал «Микропроцессорные средства и
системы» (этот журнал был тогда единственным, в котором публиковались материалы
о персональных компьютерах). Статью отклонили из-за отрицательного отзыва
рецензента, суть которого (отзыва) сводилась к тому, что цветные дисплеи и
принтеры у нас еще не скоро появятся. Кроме того, рецензент признавался, что он
дальтоник и для него цвет в программах – это только рябь в глазах. Статья с
идеей цвета в программах была опубликована в четвертом номере журнала «Наука и
жизнь» (http://nauka.relis.ru) за 1986
год. Там же на цветной вкладке были помещены раскрашенные программы, подобные
тем, какие показаны на рис. 3 и рис. 4.
Программа – это по образному
выражению одного из теоретиков программирования Э.Дейкстры (E.Dejkstra),
сумма алгоритма и структуры данных. Как можно использовать цвет для выделения
алгоритма (порядка выполнения записанных в программе операторов через циклы,
альтернативы и прочие управляющие конструкции), показано на рис. 3 и рис. 4.
Но цвет можно приложить и к структуре данных. Пакет Mathcad в этом плане предоставляет
уникальную возможность расцвечивать переменные для выделения их структуры –
принадлежности к той или иной группе переменных.
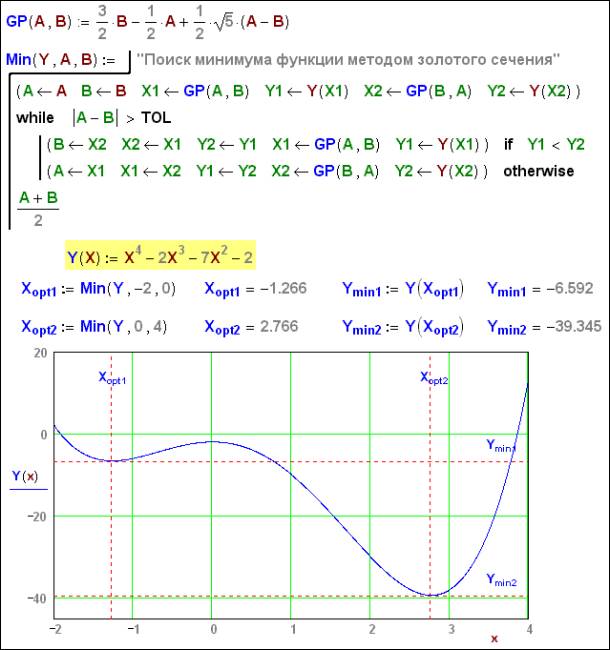
Рис. 5. Mathcad-программа «Золотое сечение» с «цветной» структурой данных
На рис. 5 программа поиска минимума функции методом
золотого сечения (см. рис. 2, рис. 3 и рис. 4,
где эта программа реализована на языке BASIC) переписана для Mathcad,
цвет в операторах которой имеет такую нагрузку:
·
черный
цвет – встроенные конструкции языка (while, if и др.)
и системные переменные (TOL – точность расчета)
·
синий
цвет – пользовательские функции и переменные
·
коричневый
цвет – формальные переменные, не принимающие никакого числового значения и
служащие только для создания пользовательских функций и операторов
·
зеленый
цвет – локальные переменные программ
·
серый
цвет – константы и комментарии
На рис. 5 созданная программа Min сразу тестируется – с ее помощью найдены
локальный (-1.266; -6.592) и глобальный (2.766;
-39.345)
минимумы полинома четвертой степени. Полученное решение отображено на графике[16].
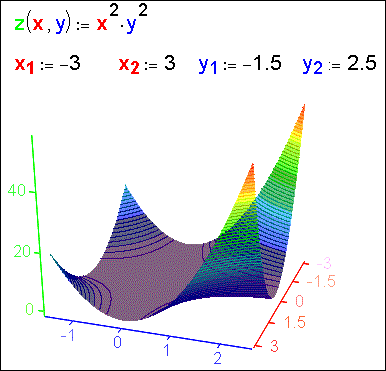
Программа на рис. 6 иллюстрирует тот факт, что белый цвет
на белом фоне – это тоже цвет (см. отдельную статью на эту тему «Переменная невидимка»). Белый цвет имен
переменных и функций на белом фоне делает их невидимыми, что, как это не
покажется странным, делает Mathcad-документ более «читабельным» (см. сноску 4). Дело в том, что чтению документа мешает не
только недостаток информации, но и ее избыток, связанной с особенностями той
или иной программной среды. На рис. 6 создана
функция с невидимым именем, которая переводит арабское число в римское, а
римское в арабское[17].
Рис. 6. Программа работы с римскими числами
Один из современных методов решения задач основан на применении компьютерных
аналитических преобразований. И тут цвет помогает лучше понимать суть и
особенности символьных вычислений. Так на рис. 7 в
пункте 1 решается квадратное уравнение, неизвестная которого выделена цветом. В
пункте 2 показана технология реализации в среде Mathcad другой популярной
операции – подстановки: в исходном выражении переменная x (красный цвет) заменяется на выражение, переменные
которого зеленые. В пункте 3 ищутся коэффициенты полинома, заданного в неявном
виде по отношению к переменной z (зеленый цвет).

Рис. 7. Цвет в символьной математике Mathcad
Послесловие
Программа
на рис. 3 отвечает принципу единства формы
и содержания: она использует метод золотого сечения и вписана в
структурную диаграмму, стороны которой находятся в золотой пропорции
(отношение высоты к ширине равно отношению ширины к сумме высоты и ширины[18]).
Золотое сечение (пропорция) – это одна из тех бесценных «ниточек», которые
связывают науку и искусство. С одной стороны, золотое сечение очень часто
присутствует во многих образцах изобразительного искусства. С другой стороны,
если говорить о математике (царица наук), то золотое сечение помогло нам в
программе на рис. 3 более оптимально найти
минимум функции. Один из универсальных методов поиска решения задачи на
компьютере основан на половинном делении (сечении): интервал неопределенности
делится пополам, далее пополам делится та половина, где находится решение и
т.д. Этот метод часто иллюстрируют описанием поимки льва в Сахаре: пустыня
перегораживается забором, далее перегораживается забором та половина, где
оказался лев. Эта процедура повторяется до тех пор, пока лев не окажется в
ящике (пока не будет выполнено условие по точности решения задачи). Если искать
минимум методом половинного деления, то придется дважды высчитывать значение
анализируемой функции – функции, у которой ищется минимум. Если же делить
отрезок неопределенности в золотом соотношении, то будет достаточно высчитывать
значение анализируемой функции только раз. Это простейший пример тесного
переплетения эстетики и утилитарности. В качестве более сложного примера можно
привести уверенность опытных инженеров в том, что крепким и долговечным может
быть только красивый мост[19]
или любое другое сооружение.
Новые примера использования цвета в Mathcad-документах:
Одинаковый цвет переменных и осей графика

Цвет переменный соответствует ее названию
Отклики
Очень интересно и созвучно с моим мнением.
В какой-то мере в работе со студентами (в MathCAD'е) я тоже стараюсь использовать цвет и шрифт. В этом отношении мне больше нравится Turbo Pascal for Windows / Delphi. Мне кажется, что с точки зрения оформления программы там сделано лучше (просто и элегантно).
Когда-то с этой целью для DOS'а использовал редактор Multi-Edit 7.0, который поддерживал выделение цветом для разных языков программирования, в том числе и для BASIC'а.
А так вполне с Вами согласен - в учебных программах использование цвета просто необходимо (главное - чтоб все в меру, чтобы не было, как у нас говорят, разноцветное, как цыганская кобыла).
С уважением, Владимир Мороз (vmoroz58@yahoo.com)