Булевы кубики

Валерий Очков (ochkov@twt.mpei.ac.ru)

Есть переменные, которые могут[1] принимать только два значения: 1–0, Да–Нет, True–False. Эти переменные выступают в качестве аргументов функции[2], возвращающих также только два значения [1]. Поговорим об этих переменных и функциях[3], но не в традиционном стиле классической математики, а отталкиваясь от проблем, возникающих при работе в средах тех или иных языков программирования, да и вообще, при использовании цифровой вычислительной техники, в основе которой лежит двоичный «атом» – элементарный элемент памяти, находящийся в одном из двух состояниях (заряжено–разряжено, намагничено–размагничено и т.д.). Из «атомов» (биты) составляются «молекулы» (байты), которые, в свою очередь, формируют новые «соединения» – переменные, массивы переменных – все то, чем оперируют программисты.

1. Азы двоичной математики (алгебры)

1.1. Функции одного аргумента

Таких функций четыре (f₁ – f₄ – см. табл. 1), но на практике работают только с одной – с f₁, которую называют отрицанием (инверсией).

Таблица 1. Двоичные функции одного двоичного аргумента
a	f1	f2	f3	f4
0	1	0	1	0
1	0	1	1	0
Обозначение	Øa Not(a) !a ā	a	1	0

1.2. Функции двух аргументов

Таких функций уже шестнадцать – см. табл. 2.

Таблица 2. Двоичные функции двух двоичных аргументов
a b	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15	f16
0 0	0	0	1	0	1	1	1	1	0	0	1	1	0	0	1	0
0 1	0	1	0	1	0	1	0	1	0	1	1	0	0	1	1	0
1 0	0	1	0	1	1	0	0	1	1	0	0	1	1	0	1	0
1 1	1	1	1	0	1	1	0	0	0	0	0	0	1	1	1	0
Обозначение	Ù * ´ •[4] И And & && min	Ú + ИЛИ Or ½½ max	« º Û = Eqv ==	Å ¹ <> >< Xor !=	® Ê Þ Imp ≥	® Ê Þ Imp ≤	¯ ØAnd	½ ØOr	>	<	Øa	Øb	a	b	1	0

Табл. 2 делится на две половинки – на «именную» (f₁ – f₈) и безымянную (f₉ – f₁₆). Вот имена первых восьми[5] функций:

· f₁ – конъюнкция (логическое умножение)

· f₂ – дизъюнкция (логическое сложение)

· f₃ – равнозначность (эквивалентность, тождественность)

· f₄ – неравнозначность (неэквивалентность, разделительная дизъюнкция, сумма по модулю 2)

· f₅ и f₆ – импликация (f₅ – импликация от a к b; f₆ – импликация от b к a, логическое следование)

· f₇ – функция (стрелка) Пирса (функция Вебба, функция Даггера, антидизъюнкция)

· f₈ – функция (штрих) Шеффера (антиконъюнкция)

Остальные восемь функций табл. 2 (f₉ – f₁₆, как, впрочем, и три последние функции табл. 1) не имеют ни имен, ни практического применения. Это либо константы (f₁₅ и f₁₆), либо функции только одного аргумента (f₁₁ – f₁₄). Имя, да и то условно, можно дать только функциям f₉ и f₁₀ – инверсия импликации.

Семь комментариев к табл. 1 и табл. 2:

1. В табл. 1 и табл. 2 собраны имена функций и символы операторов по всем двадцати позициям (4+16). Для этого пришлось несколько схитрить – «притянуть» в круг двоичных функций операторы, прямо для этого не предназначенные: «>» (больше) и «<» (меньше), например. Эти операторы хоть возвращают двоичный результат, но предназначены для работы с вещественными, а не с двоичными операндами. Этой особенности (ее можно назвать «заглавной» особенностью статьи) мы еще коснемся в пункте 7.

2. В табл. 1 и табл. 2 автор попытался собрать все имена функций и символы операторов, использующихся для реализации двоичной арифметики. Список, конечно, неполный. Читатель может расширить его примерами из других языков программирования (Pascal, fortran и др.) и математических программ (Maple, MatLab, Mathematica и др.).

3. Можно отметить избыточность функции в табл. 1 и табл. 2. В языках программирования программисту предоставляется некий ограниченный набор встроенных двоичных функций и операторов. Вот их перечень таких функций и операторов, встроенных в популярные программные среды:

· язык BASIC: Not, And, Or, Xor и Imp

· язык C: !, &, &&[6], !=, ║ и = =

· среда Mathcad: ¬, Ù, Ú и Å[7]

Недостающие двоичные функции (операторы) программист может ввести в программу через механизм пользовательских функций.

Но деление двоичных функций и операторов на основные (базисные) и вспомогательные появилось задолго до компьютеров и «узаконилось» в виде двоичных алгебр (в скобках отмечен их базис):

• алгебра логики (¬, &, Ú, ® и «)
• булева алгебра (¬, & и Ú)
• алгебра Жегалкина (&, Ú и Å)
• алгебра Пирса (¯)
• алгебра Шеффера (│)

Две последние двоичные алгебры примечательны тем, что в их базисе всего лишь одна двоичная функция, опираясь на которую можно построить все остальные.

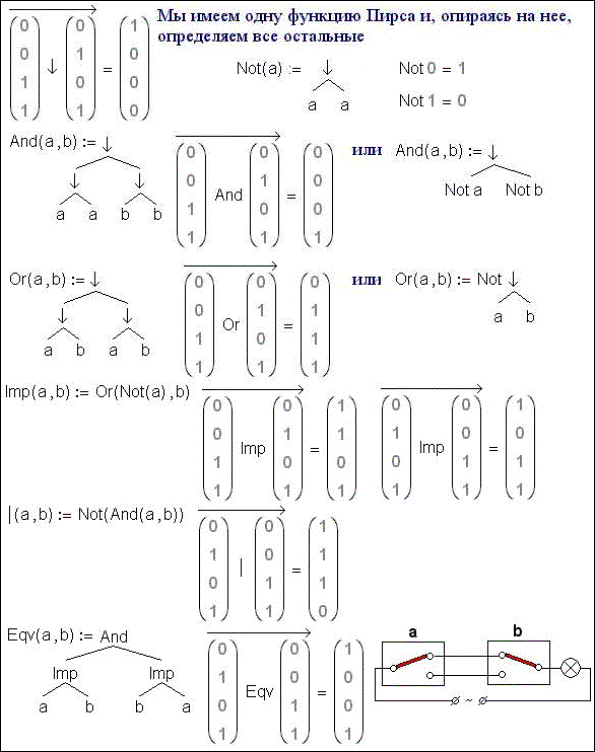
Рис. 1. Построение двоичных функций с опорой на функцию Пирса

На рис. 1 показан Mathcad-документ, где с опорой на функцию Пирса (еще говорят – стрелка Пирса: ¯) построены другие двоичные функции[8]: одна двоичная функция одного аргумента (отрицание, инверсия – Not) и пять двоичная функций двух аргументов: And, Or, Imp, штрих Шеффера и Eqv. Последние три функции (Imp, штрих Шеффера и Eqv) определены с использованием ранее определенных функций. Это сделано для большей компактности рисунка, но от механизма вложения пользовательских функций (Imp(a, b) := Or(Not(a), b, например) можно отказаться и оперировать «для чистоты эксперимента» только функцией (штрихом) Пирса. Двоичные функции часто иллюстрируют электрической цепью: последовательное соединение выключателей – это конъюнкция, а параллельное – дизъюнкция. На рис. 1 показан менее тривиальный пример – электрический аналог эквиваленции: схема соединения двух выключателей, так чтобы свет независимо зажигался и тушился из двух мест.

На алгебру Пирса и алгебру Шеффера возлагались большие надежды в смысле построения компьютера[9] из однотипных элементов. Потом от этой идеи отказались по ряду причин, главная из которых в том, что любой компьютер и так состоит только из однотипных элементов – из транзисторов, объединенных в интегральные микросхемы (чипы).

4. Можно отметить недостаточность набора математических инструментов, отображенных в табл. 1 и табл. 2 (Если объединить пункты 3 и 4 наших комментариев, то их можно поместить под одним заглавием «Избыточная недостаточность» [2]). Возьмем, например, самую «популярную» функцию двоичной алгебры конъюнкцию[10]. Ее столбец в таблице истинности (а так называют табл. 1 и табл. 2.) по идее должен быть такой:

Таблица 3. Уточненная конъюнкция
a b	a And b (f1)
0 –	0
0 –	0
1 0	0
1 1	1

Прочерк на месте нуля означает то, что если первый (a) аргумент равен нулю, то незачем проверять, чему равен второй аргумент (b), и наоборот. Так и поступают, строя некоторые языки программирования – C, например. При программировании в среде языка BASIC условный переход по конъюнкции можно записать так:

If a And b Then… (1-й способ)

но лучше так:

If a Then If b Then… или If b Then If a Then… (2-й способ)

Второй способ записи позволяет не только ускорять расчеты, но и избегать некоторых ошибок – логическое выражение b может иметь смысл, если на альтернативный вопрос a дан положительный ответ. Вот типичный пример такой «программистской» ситуации:

If I > 0 Then If V(i) > V(i-1) Then…

Можно сказать, что в языке BASIC есть две конъюнкции: And и Then If.

Если учитывать то, что в статье рассматривается не какая-то конкретная алгебра двоичных чисел (булева, Пирса, Шеффера и т.д.), а перечисляются возможные двоичные функции двоичных аргументов, то следует признать, что даже одноместных функций должно быть не четыре (см. табл. 1), а… бесконечное множество. Запрограммированная двоичная функция может, например, возвращать единицу с вероятностью 70%, если ее аргумент равен нулю, и с вероятностью 30%, если аргумент равен 1. В остальных случаях она возвращает нуль.

5. В табл. 1 и табл. 2. мы собрали двоичные функции одного (табл. 1) и двух (табл. 2) аргументов. Но, возвращаясь к конъюнкции, можно сказать эта функция имеет не два, а… полтора аргумента – см. табл. 3.

Такую же нецелочисленность (вещественность!) или непостоянство числа аргументов можно отметить и по другим двоичным функциям:

Таблица 4. Двоичные функции полутора, одного и нуля аргументов
a b	a Or b (f2)	a b	a (f11)	Øa (f13)	a b	b (f12)	Øb (f14)	a b	1 (f15)	0 (f16)
0 0	0	0 –	0	1	– 0	0	1	– –	1	0
0 1	1	0 –	0	1	– 1	1	0	– –	1	0
1 –	1	1 –	1	0	– 0	0	1	– –	1	0
1 –	1	1 –	1	0	– 1	1	0	– –	1	0

6. Можно отметить, что в табл. 2 попали операторы, изначально предназначенные для работы не с двоичными[11], а с вещественными операндами: «>», «<», «≥», «≤», «=» и «≠». Но если принять во внимание тот факт, что множество двоичных чисел[12] входит во множество вещественных чисел[13], то включение этих операторов в табл. 2 вполне законно. В этом ряду («>», «<», «≥», «≤», «=» и «≠») также можно отметить и избыточность и недостаточность. С избыточностью все более-менее ясно («больше», например, – это инверсия от оператора «меньше или равно» и т.д.). Недостаточность же можно наблюдать в том, например, что при работе с вещественными переменными вместо оператора «равно» более уместно использовать оператор «примерно равно», которого нет в списках встроенных. Можно также вспомнить о существовании понятий «намного больше» или «намного меньше». Эти операторы соотношения также возвращают двоичные значения, но имеют фактически уже не два, а три аргумента (операнда): сравниваемую пару вещественных чисел и некое контекстное представление программиста о том, что такое «примерно» или «намного».

7. Если говорить не о классической двоичной алгебре, а о реальной практике программирования, то следует признать, что переменные, фигурирующие в табл. 1 и табл. 2 могут принимать не два (0 или 1), а три значения: 0, 1 и неопределенно. Эту особенность мы уже зафиксировали в табл. 3 и в табл. 4, где вместо конкретных значений аргументов (0-1) стоит прочерк. В языках программирования есть инструменты, обработки таких «прочерков» в таблицах истинности. Если аргумент двоичной функции не определен, то расчет может либо прерываться сообщением об ошибке, либо идти по третьему пути.

Аргументы двоичных функций могут принимать не два и не три, а… бесконечное множество вещественных значений. Это множество делится на две предельно неравные части: на нуль и на ненуль (Ø0, если говорить языком табл. 1 – на числа, отличные от нуля, которые двоичными функциями воспринимаются как единицы). Бывает и так, что двоичная функция возвращает не только нули и единицы. Вот, например, как работает функция Or в одной из реализаций языка BASIC[14]:

Таблица 5. «Дизъюнктивная конъюнкция»
a	b	a Or b
0	0	0
0	Ø0	1
Ø0	0	1
Ø0	Ø0	2

Можно допустить и такую работу расширенного оператора Or:

Таблица 6. Расширенная конъюнкция (дизъюнкция)
a	b	a Or b
0	0	0
0	Ø0	1
Ø0	0	2
Ø0	Ø0	3

Одно дело, когда первый аргумент (операнд) не равно нулю, а другое – когда второй, и третье – когда оба одновременно.

Подытоживая «семипунктный» разбор табл. 1 и табл. 2, можно сказать, что описываемые двоичные функции в реальных компьютерных реализациях могут иметь недвоичные аргументы и возвращать опять же недвоичные результаты. Но особого недвоичного смысла в этом нет. Просто по технологическим причинам вещественные переменные в описываемых реализациях языков программирования (BASIC, Mathcad и др.) «по совместительству» выполняют роль двоичных (булевых, логических). При этом двоичные (булевы, логические) функции воспринимают свои вещественные аргументы «двоично»: нуль есть нуль («Нет», «False»), а все остальное единица («Да», «True»).

Эта, можно сказать, «категоричность» описываемых встроенных функций вступает в противоречие с положениями теории нечетких множеств (fuzzy sets) и теории нечеткой логики (fuzzy logic –[3, 4]). Необходимо, например, статистически обрабатывать на компьютере не только «черно-белые» (двоичные) ответы анкетируемых типа «Да (1)» – «Нет (0)», но и «цветные» (вещественные) ответы: «Да (1)», «Скорее да, чем нет (0.75, например)», «Ни да, ни нет (0.5)», «Скорее нет, чем да (0.25, например)» и «Нет (0)». Если говорить не о статистике[15], а об электротехнике и вернуться к электрическим цепям, которыми иллюстрируют работу двоичных функций (см. нижнюю часть рис. 1), то можно упомянуть тот факт, что сейчас в быту получают распространение выключатели, плавно меняющие накал ламп от 100% до нуля. Еще раньше, такие устройства стали применять в театрах и кинозалах. Медики уверяют, что плавный переход от света к темноте через полумрак не портит зрение. (В кинотеатрах свет тушат плавно, конечно, не по медицинским соображениям, а по другим причинам – если резко погасить свет, то может начаться паника.)

Можно привести еще множество примеров, толкающих к тому, что аргументами функций, перечисленных в табл. 1 и табл. 2 могут и должны быть не только двоичными, но и вещественными числа, плавно меняющиеся от нуля до единицы. И возвращать функций, перечисленные в табл. 1 и табл. 2, должны вещественные значения, опять же плавно меняющиеся от нуля до единицы. Вот как, например, можно задать «плавную» функцию отрицания:

Not(a) := 1-a

«Плавная» конъюнкции и «плавная» дизъюнкция получаются сами собой, если вспомнить о том, что одно из обозначений конъюнкции – это min (см. столбец f₁ в табл. 2), а одно из обозначений дизъюнкции – это max (см. столбец f₂ в табл. 2).

AND(a, b) := min(a, b)   OR(a, b) := max(a, b)

Несложно задать и другие «плавные» двоичные функции:

EQV(a, b) :=1 – |a – b|   XOR(a, b) :=1 – EQV(a, b)

Для иллюстрации функций двух переменных требуются уже не линии, а поверхности. На рис. 2 показаны, если так можно, выразится заглавные «булевы кубики» – поверхности «плавных» двоичных функций (AND, OR, EQV, XOR), которые при двоичных аргументах полностью повторяют работу своих традиционных «четких» аналогов (And, Or, Eqv, Xor), но при вещественных аргументах возвращают также вещественные значения, плавно меняющиеся от 0 до 1.

Рис. 2. Булевы кубики

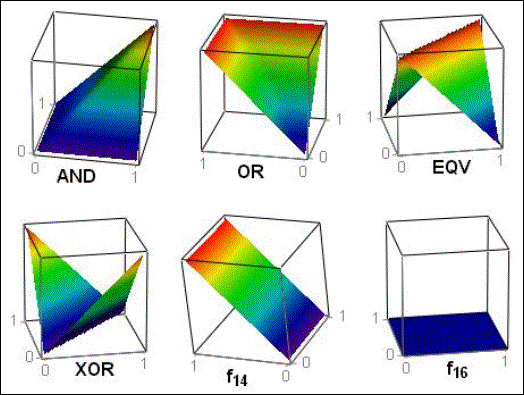
Если вращать кубики, показанные на рис. 2, то можно увидеть все 16 функций из табл. 2:

· Вращаем кубик AND вокруг вертикальной оси – получаем функции f₇, f₉ и f₁₀ (три единицы внизу, а одна наверху)

· Вращаем кубик OR (его можно получить, перевернув вверх ногами кубик AND) вокруг вертикальной оси – получаем функции f₅, f₆ и f₈ (три единицы наверху, а одна внизу)

· Вращаем кубик функции f₁₄ вокруг вертикальной оси – получаем функции f₁₁, f₁₂ и f₁₃ (две единицы внизу, а две наверху)

· Переворачиваем вверх дном кубик функции f₁₆ (четыре единицы внизу) – получаем функцию f₁₅ (четыре единицы наверху).

1.3. Функции многих аргументов

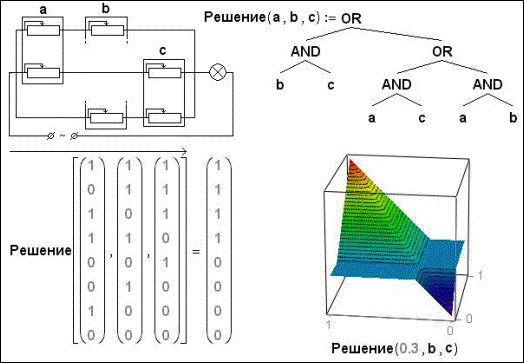
На рис. 3 показано формирование в среде Mathcad «плавной» функции трех аргументов, возвращающей решение жюри присяжных, которые могут выдавать уже не «черно-белые» ответы (виновен – невиновен), а… «цветные»: виновен на 30%, невиновен на 70%, например. В электрическом аналоге машинки для голосования выключатели заменены на реостаты.

Рис. 3. Машинка для нечеткого (мягкого, рейтингового) голосования

Функция Решение, показанная на рис. 3, при двоичных аргументах возвращает двоичный ответ, а при вещественных – вещественный, естественно. На рис. 3 показан соответствующий «булев кубик» при a=0.3 – мы видим гибрид конъюнкции с дизъюнкцией: мнение одного члена жюри переводит вердикт из области OR в область AND.

Литература:

1. Есипов А.С. Логические основы построения и работы компьютеров. Компьютерные инструменты в образовании (http://www.aec.neva.ru:8081/journal). 1’2000

2. Очков В.Ф. Принцип неопределенности программирования. КомпьютерПресс, 7’1996 (http://twt.mpei.ac.ru/ochkov/IZBYT.htm)

3. Очков В.Ф. Mathcad и нечеткие множества. КомпьютерПресс, 1’1998 (http://twt.mpei.ac.ru/ochkov/F_sets.htm)

4. Очков В.Ф. Mathcad и нечеткая логика. КомпьютерПресс, 8’1998 (http://twt.mpei.ac.ru/ochkov/F_log.htm)

---

[1] Здесь уместнее сказать не «могут», а «обязаны». Эта стилистика – одна из тем статьи.

[2] Или в качестве операндов операторов. Под функцией или оператором (встроенной или пользовательской) мы будем понимать две формы записи самой распространенной программистской конструкции: конъюнкцию, например, можно вызывать в виде функции – And(a, b) или в виде оператора – a Ù b.

[3] Их называют двоичными функциями, функциями алгебры логики, функциями булевой алгебры и т.д.

[4] Знак умножения может опускаться – a×b или a b. Тут имеет место некоторая путаница – пользователь может пробел (невидимый знак) принимать не только за знак умножения, но и за знак сложения:

1 км 200 м = 1 км и 200 м = 1 км + 200 м = 1200 м

[5] Вернее, семи («великолепная семерка»): две функции (f₅ и f₆) называются одинаково – импликация.

[6] & – это логическое умножение, а && – побитовая конъюнкция.

[7] Эти операторы были встроены только в 2000-ю версию Mathcad. Но пользователи Mathcad уже давно научились разными методами реализовывать конъюнкцию и дизъюнкцию. Для этого либо использовались арифметические действия «помножить» и «сложить», либо вводились пользовательские функции And и Or.

[8] Такая задача – неплохая тема лабораторной работы по основам информатики. Мы выбрали в качестве «рабочего стола» Mathcad потому, что в нем есть инструмент вызова функции двух аргументов в виде древовидного оператора, что существенно повышает «читабельность» документа. Кроме того, в среде Mathcad позволительно давать пользовательским функциям и операторам имена не только в виде цепочки литер (так обычно задают функции), но символом, который закрепился за той или иной математической операцией задолго до появления компьютеров. Пример – стрелка Пирса и штрих Шеффера на рис. 1. Это одна из причин популярности Mathcad.

[9] Имеется в виду цифровой компьютер. Мы уже как-то забыли, что были, а где-то еще и есть аналоговые вычислительные машины.

[10] Следствие ее популярности и в том, что у нее больше всего имен и символов для обозначения – см. столбец f₁ в табл. 2.

[11] Программисты такие переменные называют по-разному: логические, булевы, двоичные, битовые т.д., подразумевая при этом не какую-то конкретную двоичную алгебру, а то, что такие переменные принимают всего два значения.

[12] Здесь о «множестве» говорить не приходиться: «Раз, два…и обчелся», но см. пункт f наших комментариев.

[13] Входит не по смыслу двоичных алгебр, как бы «технологически» – с точки зрения программиста, объявляющего типы переменные для последующей работы с ними.

[14] Язык BASIC, которым комплектовалась популярная в свое время ПЭВМ «Искра-226» (http://www.ic.kz/~ksxi/musei/int6.htm калька машины «Wang-2000»)

[15] Уинстон Черчилль говорил, что есть Большая ложь, Просто ложь и… Статистика.