УДК 621.12.62-5
Анализ изотерм ионного обмена в среде Mathcad
Очков В.Ф.[1], Пильщиков А.П., кандидаты техн. наук, Солодов А.П., доктор техн. наук, Чудова Ю.В., аспирант
Московский энергетический институт
Данная
статья является третьей из цикла статей, публикуемых в «Теплоэнергетике» и
затрагивающих тему использования физико-математического пакета Mathcad[2] для
расчетов в области теплоэнергетики. В статье проанализировано распространение
волн концентраций в ионитных фильтрах методом характеристик. Показано формирование
обрывного фронта концентраций, возникающего при выпуклых изотермах адсорбции.
Введение
Изотермы ионного обмена определяют движение поглощаемых ионов и входят в математическую модель работы ионитных фильтров — основного технологического оборудования тепловых и атомных электростанций. Стадия работы ионитного фильтра происходит при выпуклой изотерме. Обмен ионов в условиях выпуклой изотермы позволяет увеличивать концентрацию их в ионите по сравнению с их концентрацией в растворе. Регенерация осуществляется в условиях вогнутой изотермы. Для анализа математической модели работы ионитных фильтров в данной работе используется математический пакет Mathcad. Mathcad легок в изучении и это выгодно отличает его от других программ компьютерной математики. Для работы в нем не требуется специальных навыков программирования, а значит ускоряется и постановка и решение задачи. Рабочий лист легко компоновать — не составит труда поместить рядом с математическими формулами или программой поясняющий текст, рисунок, анимационный клип. Если на какое-то время прекратить пользоваться пакетом, то впоследствии можно легко вернуться к работе с ним. В других же программах компьютерной математики часто используется сложный синтаксис, который быстро забывается, если не работать с ними постоянно. При этом, пакет Mathcad позволяет решать широкий круг научных, инженерных и учебных задач. Mathcad обладает мощными графическими средствами которые позволяют наглядно показать результаты расчетов. Кроме того, эта среда является относительно доступным инструментом, в целом наиболее «демократичным» из всех известных математических программных пакетов.
Постановка задачи
Через колонку постоянного сечения, равномерно заполненную ионитом, с постоянной скоростью пропускают раствор, содержащий извлекаемое вещество. Рассмотрим случай, когда ионит, насыщенный противоионами А, приводится в соприкосновение с раствором, содержащим ионы B. В этом случае происходит обмен ионов: часть ионов А заменяется в ионите ионами В, а часть ионов В в растворе — соответственно ионами А.
![]() .
.
На рис. 1 схематически показано устройство ионитного фильтра.
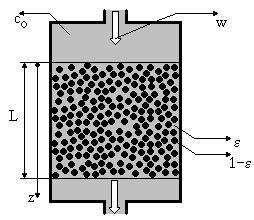
Рис. 1. Схема ионитного фильтра
Примем направление вдоль колонны за ось z. Обозначим через q(z, t) концентрацию ионов В, содержащуюся к моменту времени t в ионите на расстоянии z от входа в колонку, а через c(z, t) — концентрацию этого вещества в растворе. Вода, поступающая в фильтр, содержит примеси в концентрации c0[г/м3раств].
Объемная доля воды задается пористостью ε. Объемная доля ионита составляет величину (1-ε).
Говоря о пористом слое, мы имеем ввиду некоторый объем, на долю ε заполненной водой и на долю (1-ε) — гранулами сорбента.
Концентрацию с относят к единице объема раствора, а q — к единице объема слоя. В этом случае связь между концентрациями описывается уравнением:
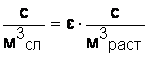 (1)
(1)
Поскольку рассматриваемая система состоит из воды и гранул ионита, то есть является двухфазной, то необходимо точно указывать к какому объему или сечению относятся величины.
Расход воды задается величиной эквивалентной скорости wэ[м/c], которая представляет собой отношение скорости движения раствора в свободном сечении фильтра w к доле свободного сечения зернистого слоя:
![]() (2)
(2)
Пока концентрация примесей, задержанных ионитом, меньше значения полной обменной емкости q0, будет происходить очистка воды. Задача разрабатываемой модели – описание пространственно-временного распределения концентрации в фильтре.
Расчетные уравнения работы ионитных фильтров
В неравновесных условиях математической моделью работы фильтра является система уравнений, состоящая из уравнения материального баланса, внешнедиффузионной кинетики и статики обмена.
Если рассматривать движение однокомпонентного раствора только вдоль оси фильтра и пренебречь продольной диффузией поглощаемого иона, то уравнение материального баланса имеет вид:
![]() (3)
(3)
Уравнение внешнедиффузионной кинетики получают, исходя из баланса, согласно которому изменение концентрации поглощаемого иона в ионите в единицу времени (∆q/∆t) пропорционально изменению концентрации этого иона в растворе (∆с=с-с´). Окончательное уравнение записывается для бесконечно малого изменения концентрации иона примеси в ионите за бесконечно малый промежуток времени:
![]() (4)
(4)
где с´ - равновесная концентрация иона в растворе, граничащем с поверхностью ионита;
β - коэффициент массопереноса, м3 пор/м3т.ф.∙с.
Последнее уравнение – уравнение статики обмена называют изотермой обмена:
q=q(c) (5)
При построении математической модели ионитного фильтра, работающего в равновесных условиях, считают, что при течении через слой ионита раствора поглощаемого иона на любом сколь угодно малом слое равновесие обмена достигается мгновенно. Это позволяет не учитывать скорости перехода поглощаемого иона, так как концентрации в растворе и на поверхности ионита равны. В этом случае математическая модель работы фильтра включает дифференциальное уравнение (3) и уравнение изотермы ионного обмена (5).
Граничными условиями системы будут:
c(0 , с)=c0
q(z , 0)=0
Первое равенство указывает на то, что над слоем ионита z=0 в любой момент времени t находится раствор с постоянной концентрацией c0. Второе означает, что первоначально (τ=0) на любой высоте слоя ионита z поглощаемый ион В отсутствует.
Волновое уравнение для концентрации
Используя уравнение изотермы ионного обмена (5), можно исключить концентрацию q примесей в ионите из уравнения материального баланса (3).
Функция q является сложной функцией двух переменных: τ и c, поэтому ее частную производную можно представить в виде:
![]() (6)
(6)
и преобразовать уравнение материального баланса
![]() (7)
(7)
Учитывая, что скорость w есть постоянная величина, после приведения подобных членов и других простых преобразований приходят к волновой форме записи уравнения сохранения:
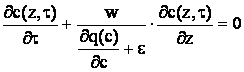 (8)
(8)
Обозначим множитель перед ![]() :
:
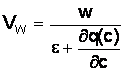 (9)
(9)
Он имеет смысл волновой скорости, то есть является скоростью перемещения по слою ионита раствора с заданной концентрацией поглощаемого иона и называется скоростью перемещения концентрационных точек фронта.
Уравнение сохранения в безразмерной форме
Запишем уравнение сохранения в безразмерной форме для работы ионитных фильтров в равновесных условиях при пропускании однокомпонентного раствора. Рассмотрим случай, когда в колонке не протекают побочные реакции с выделяющимися из ионита ионами. Перейдем к следующей системе безразмерных переменных и параметров. Независимые переменные координата и время вводятся следующим образом:
 (10)
(10)
Относительная концентрация примеси в растворе, зависимая переменная:
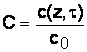 (11)
(11)
Относительная концентрация примеси в ионите:
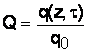 (12)
(12)
где q0 – суммарное содержание ионов А и В в ионите:
q0=qA+qB
Распределительное отношение:
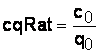 (13)
(13)
Далее и в вычислительных программах пористость будем обозначать как Por,
![]() .
.
Безразмерная волновая скорость:
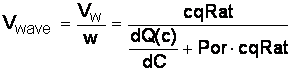 (14)
(14)
Уравнение материального баланса запишется следующим образом:
![]() (15)
(15)
Уравнение изотермы ионного обмена
Изотерма ионного обмена обычно дает зависимость концентрации противоиона А в ионите от его концентрации в растворе в равновесных условиях. Концентрация противоиона А зависит не только от его концентрации в растворе, но также является функцией общей концентрации и температуры. Изотерма обмена, как показывает само название, относится к некоторой заданной температуре.
Классическая форма изотермы при мономолекулярной адсорбции задается уравнением Ленгмюра:
![]() (16)
(16)
Из этой формулы следует, что равновесное значение q уменьшается с уменьшением начальной концентрации раствора на входе в фильтр. При больших значениях концентрации c равновесное значение q стремится к q0.
В безразмерной форме уравнение Ленгмюра имеет вид:
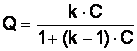 (17)
(17)
где k — концентрационная константа равновесия, зависящая от концентрации С.
При значениях k>1 изотерма адсорбции будет выпуклой в координатах Q-C, следовательно ионит предпочтительнее поглощает ионы из раствора.
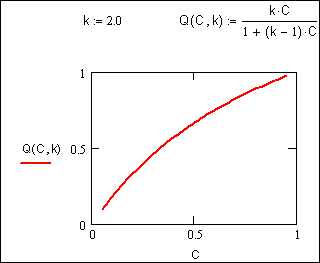
Рис. 2. Изотерма Ленгмюра
При k<<1 уравнение изотермы вогнутое.
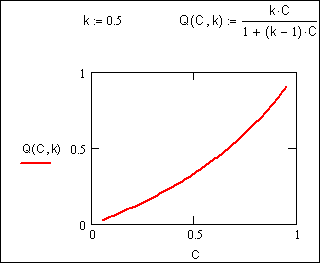
Рис. 3. Вогнутая изотерма адсорбции
В этом случае (рис. 3) k характеризует процесс вытеснения ионов из ионита.
Равенство k=1 приводит к линейной изотерме
Q=C.
Это значит, что гипотетический ионит не обладает никакой избирательностью к ионам А по сравнению с ионами В.
Решение волнового уравнения методом характеристик
Уравнение (3), к которому сведена математическая модель ионитного фильтра, представляет собой квазилинейное однородное уравнение в частных производных гиперболического типа. При решении его с помощью метода характеристик задача интегрирования уравнения (3) равносильна задаче интегрирования следующего характеристического уравнения:
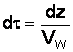 (18)
(18)
Интеграл этого уравнения
![]() (19)
(19)
является решением уравнения (3). При τ=0 характеристический интеграл становится равным: u=z. По условию задачи с есть функция z и τ и при τ=0 с=f(z),следовательно, при τ=0 с=f(u). Решением задачи, где функциональная зависимость z от концентрации представлена в явном виде является уравнение:
![]() (20)
(20)
При τ=0 функция ![]() дает начальное
распределение иона В по слою ионита.
дает начальное
распределение иона В по слою ионита.
С физической точки зрения уравнение (20) есть уравнение движения концентрационных точек фронта. Оно позволяет рассчитать распределение поглощаемого иона вдоль слоя ионита (z) для различных моментов времени.
Выпуклая изотерма. Рассмотрим случай, когда адсорбция описывается изотермой Ленгмюра (уравнение 16). Вычисления волновой скорости показаны на (рис. 4). Значения параметров, таких как пористость, распределительное соотношение и другие, указаны в качестве аргументов функции волновой скорости. Безразмерное значение концентрации на входе равно единице. Из приведенных вычислений следует, что с ростом концентрации волновая скорость увеличивается. Мы увидим далее, к каким особенностям пространственно-временного изменения концентрации примеси в ионите это приведет.
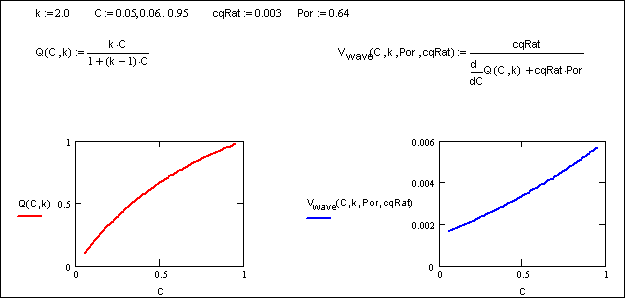
Рис. 4. Волновая скорость для фильтра, работающего по изотерме Ленгмюра
Расчет распространения волн концентрации, выполненный в Mathcad-документе, представлен на (рис. 5) и (рис. 6).
В вычислительном блоке 1 (рис. 5) сначала задается начальное распределение концентрации вдоль фильтра. В точках z0 начинаются характеристики, на которых сохраняются значения Cinit. Второе соотношение задает волновую скорость как функцию концентрации. Третье соотношение является уравнением характеристики. Дальнейшие вычисления основаны на том, что характеристики являются линиями функции C(Z, T).

Рис. 5. Вычисление характеристик, исходящих из точек z0
В блоке 2 созданы наборы значений исходных точек z0 , в которых начинаются характеристики, и моментов времени τ, для которых будут производится вычисления. В блоке 3 создана сетка на плоскости (Z, T) с узлами, проиндексированными как (i, j) и в этих узлах вычислена концентрация.
На (рис. 6) результаты расчета отражены графически. Левый график дает трехмерное представление. По вертикальной оси откладывается концентрация, левая и правая горизонтальные оси — координата Z и время T. Для построения применен параметрический способ (Parametric surface plots). Правый график — обычная двухмерная диаграмма, на которой строится зависимость концентрации вдоль фильтра для трех значений времени: исходного (индекс времени, т.е. второй индекс массива, равен 0) и двух последующих с индексами времени 40 и 80.
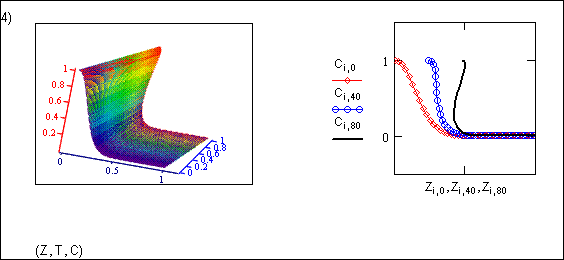
Рис. 6. Опрокидывание волны концентрации при расчете методом характеристик фильтра, работающего по выпуклой изотерме ионного обмена
При прохождении раствора через фильтр разные концентрационные точки будут двигаться с разными скоростями. Поэтому, как только появится первоначальное распределение концентраций с(z), большие концентрации, у которых ∂q/∂c мало, будут двигаться с большими скоростями, обгоняя малые концентрации, характеризуемые большими значениями ∂q/∂c. Такое положение приводит к тому, что все концентрационные точки фронта будут иметь одну и ту же координату z. В этот момент распределение концентраций с(z) исчезнет. Фронт концентраций из непрерывной дифференцируемой функции превратится в недифференцируемую, разрывную функцию.
Это противоречие между формальным решением и физическим содержанием задачи разрешается введением разрывных решений, заменяющих опрокидывание волны скачком концентраций.
В рассматриваемый момент в растворе будет всего одна концентрация, так как невозможно иметь на одной и той же высоте слоя ионита z несколько различных концентраций в растворе. Эта концентрация при движении вдоль слоя ионита должна оставаться постоянной. Таким образом, по окончании формирования обрывного фронта концентраций единственная концентрационная точка его, отвечающая максимальной концентрации раствора, будет двигаться на протяжении всего остального времени работы ионитного фильтра с постоянной скоростью. Эта скорость и будет скоростью движения всего концентрационного фронта.
Вогнутая изотерма адсорбции. Для сравнения рассчитаем распространение волны концентраций в фильтре, работающим по вогнутой изотерме (рис. 7). Значение параметра k принято равным 0.5, что и обеспечивает вогнутость. Для вогнутой изотермы волновая скорость уменьшается с ростом концентрации. Распространение фронта концентрации рассчитывается по той же программе, что и на (рис. 5) и (рис. 6). Результаты расчета показаны на (рис.8).
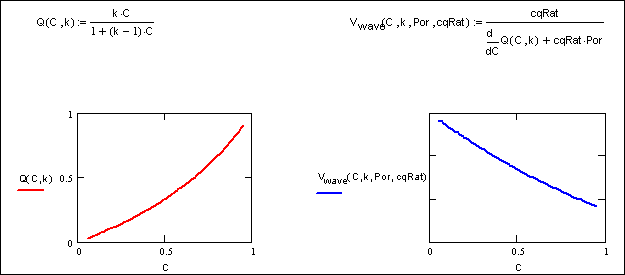
Рис. 7. Волновая скорость для вогнутой изотермы адсорбции
При вогнутой изотерме обмена концентрационные точки фронта с малыми концентрациями движутся с большими скоростями, чем концентрационные точки, характеризуемые большими концентрациями, так как при вогнутой изотерме значения производных концентрации иона в ионите по его концентрации в растворе с увеличением концентрации иона в растворе возрастают. В результате неравенства скоростей перемещения точек концентрационного фронта этот фронт в процессе пропускания раствора, содержащего ионы В деформируется так, что за один и тот же интервал времени малые концентрации проходят большие расстояния, чем большие. Концентрационный фронт размывается. Явление размывания фронта при его движении дает возможность получать производную для любой точки концентрационного фронта, так как за все время пропускания раствора распределение концентраций по высоте ионита с(z) остается непрерывной и дифференцируемой функцией.
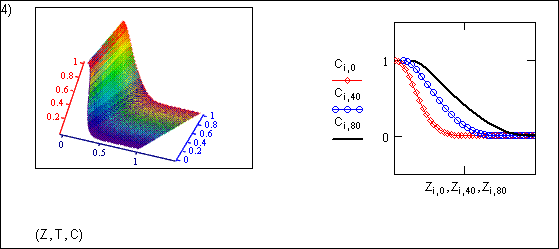
Рис. 8. Размывание фронта концентрации для фильтра, работающего по вогнутой изотерме адсорбции
Заключение
При анализе методом характеристик волн концентрации в фильтре обнаружено возникновение разрывных решений. Это характерные особенности распространения нелинейных волн. За нарушением однозначности в действительности скрывается образование ударных волн. Для воспроизведения ударных волн при численных реализациях математических моделей разработаны специальные численные методы алгоритмы.
Список литературы:
1. Теоретические основы деминерализации пресных вод. М.: «Наука», 1975.
2. Громогласов А.А., Копылов А.С., Пильщиков А.П. Водоподготовка: процессы и аппараты. М.: «Энергоатомиздат», 1990.
3.
Очков А.В., Утенков В.Ф., Орлов К.А.
«Теплотехнические расчеты в среде Mathcad». Журнал «Теплоэнергетика», 2’2000. с. 73-78.