Преподавание математики и математические пакеты

журнал «Открытое образование» – http://www.e-joe.ru, № 2, за 2013 г.

 

Очков Валерий Федорович

 

История математики в школе и вузе – это, помимо прочего, и история борьбы с… вычислительными средствами. Сначала (на уроках устного счета, например) запрещали пользоваться бумагой и ручкой, затем (при освоении счета «столбиком» ручкой на бумаге) – калькулятором и, наконец, при решении более сложных задач – компьютером с современными математическими программами Mathematica, Maple, Matlab, Mathcad, SMath, Derive и др. Вернее, прямо не запрещали и не запрещают, а говорят в том плане, что, мол, решение на компьютере школьной или вузовской задачи по математике равносильно решению задачи для устного счета (65 помножить на 9, например) на калькуляторе, что такая работа ничего не дает «ни уму, ни сердцу», что в процессе учебы важен не результат, а сам процесс и т.д. Этот запрет касается не самих вычислительных средств, которые можно и нужно осваивать с помощью специально подобранных примеров на занятиях по информатике и программированию, а применения этих компьютерных инструментов для решения задач, придуманных для уроков и семинарских занятий по арифметике, тригонометрии, линейной алгебре, математическому анализу задолго до появления компьютера. Но современные школьники и студенты этого не понимают и считают, что это один из многочисленных школьных запретов, непонятно кем и почему введенных... Более того, они уже не мыслят учебы без компьютера. А математика с ее вычислениями так и просится на компьютер.

С устным здесь счетом все более-менее ясно. Эти упражнения (да и вообще, любая математика) – прекрасная гимнастика для ума. Использование на таких занятиях калькулятора равносильно дооборудованию спортивного тренажера… гидроусилителями. Счет «столбиком» также можно рассматривать как гимнастику для ума, приводящую в порядок навыки работы с числами. Но тут подмешивается еще один довод. Считать в уме нужно уметь, если под рукой не окажется карандаша и бумаги, считать карандашом на бумаге нужно уметь, если под рукой не окажется калькулятора и т.д. Но… добывать огонь трением «нужно уметь, если под рукой не окажется» спичек или зажигалки, определять стороны света по деревьям в лесу «нужно уметь, если под рукой не окажется» компаса или навигатора и т.д. К сожалению или к счастью, с развитием цивилизации мы разучились добывать огонь трением, ориентироваться на местности и, увы, считать в уме. Школьный учитель автора не уставал повторять на занятиях по арифметике, что если мы, его ученики не научимся быстро и точно считать в уме или, по крайней мере, столбиком на бумаге, то нас будут обвешивать и обсчитывать в магазине. Сейчас, когда у всех под рукой есть калькулятор, эта мотивация освоения устного счета уже не работает. Как и довод о том, что это «прекрасная гимнастика для ума». Сейчас у школьника или студента все чаще и чаще в руках можно увидеть не простой калькулятор, отдельный или вшитый в сотовый телефон (смартфон), а компактный планшетник с установленными на нем математическими программами. Игнорировать этот а, тем более, вводить запреты уже нельзя.

Противники использования компьютеров (калькуляторов, смартфонов, планшетников), для решения школьных и вузовских задач по математике опираются также на ряд других доводов, о которых они, правда, открыто не говорят.

Во-первых, многие школьные учителя и преподаватели вузов, к сожалению, просто-напросто не умеют работать с компьютерными математическими программами. Компьютер они освоили на уровне офисных программ (текстовый редактор, табличный процессор, электронная почта, работа в Интернете), азов программирования и операционной системы, но дальше идти не хотят или не могут, оправдывая это и тем, что, мол, такие программы вредны для процесса обучения (см. выше).

Во-вторых, внедрение этих программ в учебный процесс требует кардинального пересмотра содержания и методов преподавания, а также переписывания учебников и задачников по математике или, по крайней мере, существенной их переработки.

В-третьих, вышеупомянутые компьютерные программы довольно дороги. Их не в состоянии купить наши школы и вузы. А ведь такие программы нужно иметь не только на школьных и университетских компьютерах. Необходимо, чтобы они стояли и на личных компьютерах (планшетниках, смартфонах) школьников и студентов для выполнения домашних заданий и работы в классе. Но эта проблема, сразу скажем, решаема. Фирмы-разработчики математических программ предоставляют учебным заведениям существенные скидки, а в ряде случаев передают программы бесплатно. Но с корыстной, конечно, целью. Школьники и студенты, освоив бесплатную программу, после окончания вуза, купят сами или попросят купить программу своего работодателя. Преподаватели не должны сетовать на дороговизну программ или на невозможность по разным причинам работы с пиратскими копиями [1], а должны искать пути решения этой проблемы, связываться, например, с разработчиками программ и их дилерами. Кроме того есть и бесплатные версии программ. Так, например, фирма PTC – разработчик программы Mathcad (www.ptc.com) дает возможность работать сначала с полной версией Mathcad Prime, а потом по истечение определенного срока с ее укороченной версией Mathcad Express, позволяющей, тем не менее, решать довольно сложные математические задачи. Программу SMath («русский» Mathcad) можно бесплатно скачать с сайта www.smath.info.

Вышеприведенные строки – это несколько переработанное начало уже опубликованной статьи автора [2], в которой рассматривалась данная проблема по отношению к преподаванию физики и содержались соответствующие «физические» примеры. В данной статье мы коснемся уже математики, прекрасно понимая, что эти две научные и учебные дисциплины взаимосвязаны. Недаром в нашей стране в списке специальностей, по которым защищают кандидатские и докторские диссертации, есть и «физико-математические» науки…

Три события побудили автора написать эту статью.

Однажды (перехожу к рассказу от первого лица) я помогал внучке решать такую задачу по математике: дан треугольник, у которого одна сторона равна 12 см, а один из углов, примыкающий к этой стороне, равен 120°. Сторона, лежащая напротив этого угла, равна 28 см. Найти длину третьей стороны треугольника и высоту, проведенную от заданного угла.

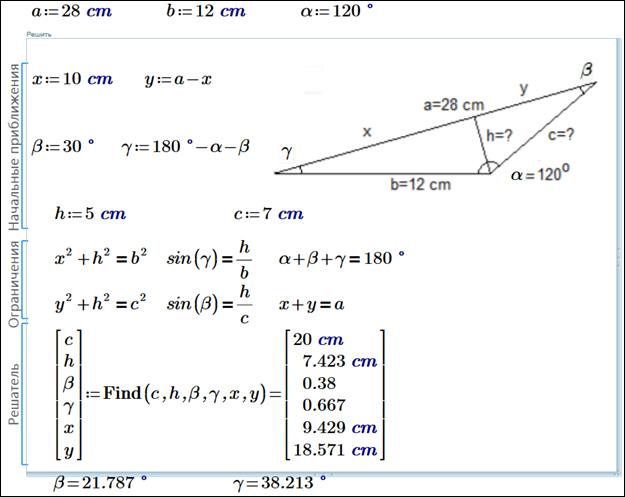
Я тут же подсел к компьютеру, составил систему шести алгебраических уравнений и без проблем решил ее в среде Mathcad с помощью решателя Solve – см. рис. 1а.

a

б

Рис. 1а. Задача о треугольнике – решение системы из шести алгебраических уравнений: Mathcad 15 (a) и Mathcad Prime (b)

В маткадовском блоке Given-Find (Solve Решить – в Mathcad Prime) нужно задать начальное приближение к решению, записать ограничения (систему уравнений) и вызвать функцию Find (Найти), которая вернет значения неизвестных, превращающих уравнения  в тождества. В решении на рис. 1 заложен KISS-принцип программирования. KISS – это аббревиатура английской поговорки Keep It Simple, Stupid – делай это проще, дурачок. В задаче можно уменьшить число уравнений до пяти, заменив, например, y на a-x. Можно оставить и четыре уравнения, дополнительно заменив γ на 180°-α-β. Можно записать вместо двух уравнений с синусами одно b·sin(180°-α-β) = c·sin(β) и т.д. Но, – делай это проще, дурачок. Замены, приводящие к уменьшению числа уравнений, ухудшают ее понимание. А для компьютера в отличие от человека нет большой разницы – шесть уравнений или пять. Если же компьютер не справится с решением, то тогда можно будет ему помочь. Но у нас решение найдено. В этом можно убедиться, подставив решение в уравнения и получив тождества.

Когда я показал это решение внучке, она сказала, что так задачи они в школе не решают и что тут нужно применить теорему косинусов, которую они в школе изучают уже чуть ли не всю четверть.

Я вспомнил, что была такая теорема, но как она выглядит – забыл напрочь. Внучка мне подсказала, что это такое. Я дополнительно справился в Интернете об этой теореме (см. http://en.wikipedia.org/wiki/Law_of_cosines)  и переписал решение задачи – см. рис. 1б.

Рис. 1б. Задача о треугольнике – решение квадратного уравнения

Я понял, что внучку и ее одноклассников учат решать квадратные уравнения (а к этому сводится наша задача о треугольнике), но не разрешают при этом использовать компьютер (см. выше) или Интернет (а там есть интерактивные решатели для таких задач) для решения систем уравнений – линейных и нелинейных, алгебраических и дифференциальных (а именно о дифференциальных уравнениях шла речь в статье [2]). А ведь многие школьные и вузовские задачи по математике, физике, химии и другим дисциплинам сводятся к решению систем уравнений. Школьнику или студенту достаточно понять суть задачи – ее «математику, физику, химию», составить систему уравнений, решить ее на компьютере и сделать проверку решения. Но нет! Школьников и студентов заставляют заучивать кучу правил и теорем, которые являются не чем иным, как готовыми решениями этих уравнений и систем. Нашу систему шести уравнений (рис. 1а) подстановками можно свести к одному квадратному уравнению, описывающему теорему косинусов, но можно этого и не делать, поручив эту работу компьютеру.

Задача на рис. 1а решена полностью – найдены длина третьей стороны треугольника и одна из его высот, о которой спрашивалось в условии задачи. Решение же, показанное на рис. 1б, неполное – нужно будет еще искать высоту треугольника. В решении, показанном на рис. 1а, тоже задействована теорема – теорема Пифагора, которую, в отличие от теоремы косинусов (теоремы Пифагора «с хвостиком»), знают все. Здесь нужно еще вспомнить, что такое синус – и все! Задача (рис. 1а) решена, а ответ даже избыточен. Подход к решению, отображенный на рис. 1а, существенно более универсален подхода, показанного на рис. 1б. Любой треугольник или даже многогранник можно разбить на отдельные прямоугольные треугольники, составить несколько систем уравнений и решить их на компьютере.

Школьные учителя «математики, физики, химии» тут сразу возразят в том плане, что теперь любой даже самый слабый школьник сможет с компьютером решить даже самые сложные задачи. А нужно, чтобы они в уме, ручкой и на бумаге делали это. Что тут возразить?! По моему опыту преподавания в вузе я знаю, что многие студенты, которым категорически запрещают использовать компьютер для выполнения типового расчета или курсового проекта и заставляют все считать «ручками на бумаге», считают все-таки на компьютере, а потом переписывают решения «ручками на бумаге», удовлетворяя желания «дремучих» преподавателей.

Да, компьютер заставляет отказываться от многих «старых добрых» задач и придумывать новые, более сложные, более интересные и более близкие к реальной жизни.

Задача о треугольнике восходит к Древней Греции – ко временам расцвета эвклидовой геометрии, когда людям нужно было измерять и межевать земельные участки. В старые времена образование делилось на классическое и реальное. В классических гимназиях старой России делали упор на изучение латыни и древнегреческого языков. В реальных училищах решали, естественно, реальные, жизненные задачи. Но отголоски «классицизма» в образовании мы видим и в современной школе при преподавании математики. Так, в задаче о треугольнике используются не современные методы решения задачи, а те, какие еще древние греки применяли. Хорошо ли это или плохо – вопрос, который поднимается в этой статье.

Да, современные компьютерные методы в школе игнорировать нельзя. Дело в том, что школьники и студенты, заучив набор правил и теорем, не могут их применять к более сложным нестандартным задачам, где упор нужно делать на «математику, физику, химию»…

Второе событие, побудившее меня написать эту статью, такое.

Несколько лет назад мне довелось читать лекции и вести практические занятия по информатике для студентов-вечерников – уже довольно зрелых и сформировавшихся людей, работающих в московских энергетических компаниях на инженерных должностях, но не имеющих высшего образования. Эти  студенты, к счастью, оказались очень хорошими. Они пришли в Московский энергетический институт не только за «корочкой» – за дипломом о высшем образовании, открывающим им карьерный рост, но и за знаниями, за пониманием тех сложных процессов производства, передачи и потребления тепловой и электрической энергии, с которыми им приходится иметь дело на работе.

Я сначала пытался читать моим вечерникам курс информатики по обычной схеме – рассказывать, что такое информация, как она создается, обрабатывается и передается с помощью современных компьютерных средств, но сразу понял, что это не совсем то, что им нужно и чем их можно увлечь.

Параллельно моему курсу информатики этим студентам читался курс математического анализа с «пределами, производными и прочими интегралами», которые их очень пугали. Компьютера же они не боялись, т.к. давно освоили его на производстве.

Мы с преподавателем математики решили объединить наши усилия и помочь студентам-вечерникам не просто освоить азы высшей математики и информатики, но и получить от этого удовольствие. А я не устаю повторять своим студентам, что от учебы, как и от любой другой трудной, но плодотворной работы нужно стараться получить не только знания и навыки, но и удовольствие. Мечтал кто-то стать артистом или летчиком, а судьба забросила его в Московский энергетический институт. Не беда! Сделай над собой усилие – полюби учебу и будущую специальность энергетика! Без удовольствия даже самая престижная и высокооплачиваемая работа может отравить всю жизнь.

Но мы отвлеклись. Вернемся к математике и компьютерам!

Я решил скорректировать программу курса информатики, вернее, изменить список примеров, которые разбирались на практических занятиях, посвященных освоению современных компьютерных средств переработки информации. Беда учебного курса по математическому анализу, который слушали студенты-вечерники, заключалась в том, что на занятиях (лекции и семинары) с горем пополам осваивалось, что такое предел, дифференциал, интеграл и как их «взять» на несложных примерах, но совсем не рассказывалось, зачем нужны эти мощные инструменты в руках инженера. Подразумевалось, что это будет дано позже – на старших курсах при чтении специальных курсов. Я решил исправить эту ситуацию и разобрать на занятиях по информатике несложные инженерные задачи с привлечением базовых понятий математического анализа.

Мои студенты-вечерники часто видели на московских ТЭЦ большие емкости (цистерны) в виде прямых круговых цилиндров для хранения мазута (топлива для ТЭЦ) или воды (рабочего тела паротурбинных энергетических блоков и теплоносителя для тепловых сетей). Такие цистерны, но уже с бензином или соляркой можно встретить и на крупных автозаправках. Мало кто задумывается о пропорциях таких цистерн: один и тот же объем жидкости можно хранить в высоком и узком или низком и широком цилиндре. Давайте докажем с помощью математики и компьютера, что при 2r = h площадь поверхности такой емкости с дном и крышкой при заданном объеме будет минимальна. На такую емкость при прочих равных условиях пойдет меньше металла, краски, теплоизолирующего покрытия. Мы со студентами-вечерниками решили эту задачу в среде программы Mathcad [3-5] с привлечением инструментов математического анализа, которые они изучали на занятиях по математике – см. рис. 2а.

 

Рис. 2а. Задача о цилиндре с минимальной площадью поверхности (Mathcad)

Формулы для вычисления объема V и площади полной поверхности S цилиндра с радиусом основания r и высотой h найти легко (например, в Интернете).

Используя инструменты символьных вычислений Mathcad, легко получить выражение для площади полной поверхности S как функции переменной r и объема V: S = S(r, V) и для ее производной S′ = S′(r, V).

Как известно, площадь поверхности может достигать искомого минимального значения в критической точке − в точке, где производная функции обращается в нуль или не существует. Поскольку производная S′(r, V) определена всюду, кроме точки r = 0,  а цилиндров с нулевым радиусом основания не бывает, то искомое значение радиуса − нуль производной S′(r, V). Находим средствами Mathcad единственный действительный корень уравнения S′(r, V) = 0. Здравый смысл (или исследование смены знака производной) подсказывают, что в этой точке достигается искомое минимальное значение S = S(r, V); при этом отношение  h/r  равно двум (как мы и собирались доказать) и от параметра (объема цилиндра) V не зависит.

А какое оптимальное отношение h к r получится для емкости конической формы?! В таких конических бункерах на электростанциях хранят, например, размолотый уголь, приготовленный для сжигания в топке парового котла. Такая оптимизационная задача была решена в среде другой математической программы Maple – см. рис. 2б.

Рис. 2б. Задача о конусе с минимальной площадью поверхности (Maple)

А что будет с решением, если у цилиндра (рис. 2а) убрать верхнюю крышку, сделать в цилиндре вертикальную центральную перегородку, накрыть цилиндр полусферой?! А что будет с решением задачи о конусе (бункере для угля – рис. 2б), если к нему приделать плоскую или сферическую крышку?! Мои студенты-вечерники увлеклись подобными оптимизационными задачами для емкостей самых различных форм, освоили азы математического анализа, а также соответствующие инструменты Mathcad и… получили удовольствие от этой работы. Эти и другие задачи выложены на сайте http://communities.ptc.com/groups/optimisation-with-mathcad.

Не остался без внимания при решении задачи о коническом бункере и «напарник» производной – интеграл. Почему в формуле объема конуса стоит одна треть (см. первый оператор на рис. 1б), а не одна вторая или одна четвертая?! Здесь можно представить конус, составленный на манер детской пирамидки из тонких цилиндров с уменьшающимися диаметрами. Объем этих цилиндров можно просуммировать и получить приближенное значение объема конуса. Далее можно толщину этих цилиндров уменьшать, а их число увеличивать до бесконечности и переходить от суммы к интегралу, заодно вспоминая, что символ интеграла – это растянутая буква s, с которой начинается латинское слово «сумма».

Подобные задачи можно и нужно разбирать не только на занятиях по информатике, но и на занятиях по математическому анализу. Чем наполнены эти занятия в настоящее время?! На лекциях даются основные понятия и доказываются некоторые базовые теоремы. А чем занимаются на практических занятиях?! Занимаются тем же «старинным устным счетом» (см. начало статьи) – «вручную», без компьютера ищут пределы функций, находят их производные, берут интегралы, раскладывают выражения в ряды и т.д. и т.п., опираясь на элементарные правила этих математических операций: производная константы, умноженной на функцию, равна константе, умноженной на производную функции, производная суммы функций равна сумме производных от функций и т.д. и т.п. Такие занятия – это, конечно, «хорошая гимнастика для ума», но мои студенты-вечерники уже знали, что есть «калькулятор» для подобных задач и не понимали, почему их заставляют выполнять «вручную» такие действия. На практических занятиях по математическому анализу можно и нужно разрешить студентам пользоваться «символьными» калькуляторами, сместив акцент занятий с техники взятия «пределов–производных–интегралов» на более глубокое понимание этих инструментов, на их практическое применение в будущей инженерной деятельности. Можно утверждать, что современные школьники и студенты изучают математику фактически по учебникам и задачникам XVIII века. Да, появились специальные курсы высшей математики с использованием современных компьютерных математических программ [3], но основная масса школьников и студентов по-прежнему учатся по учебным программам и примерам трехсотлетней давности…

Мотивация изучения «устного счета» высшей математики – приемов поиска пределов, взятия производных и т.д. у студентов пропадает не только потому, что появились «калькуляторы», быстро и безошибочно выполняющие данные операции, но и потому, что бурно развиваются и реализуются на компьютерах численные методы решения математических задач. Этими методами традиционно занималась не математика, а прикладная математика. «Настоящие математики» традиционно дистанцируются от «ненастоящих» – прикладных математиков. Есть даже такая шутливая дефиниция: «Математика отличается от прикладной математики примерно так, как государь отличается от милостивого государя». Но с развитием вычислительных средств – с повышением мощности и доступности компьютеров, с появлением новых программ численные методы стали повсеместно вытеснять аналитические методы решения задач или, по крайней мере, выступать с ними сообща, на равных.

На рис. 2в показано решение задачи о минимальной поверхности конуса, накрытого полусферой сочетанием аналитических преобразований (символьной математики) и численных методов.

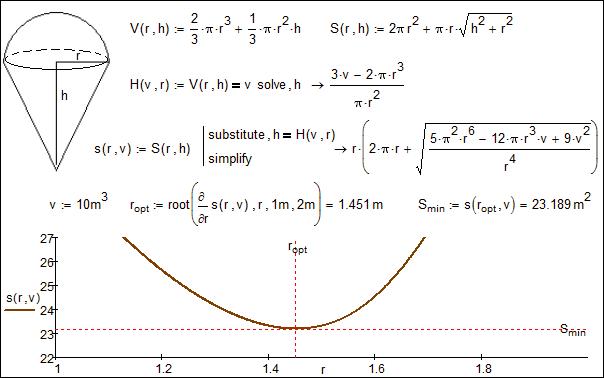
Рис. 2в. Задача о конусе и полусфере с минимальной площадью поверхности.

Конечно, очень интересно вывести формулу оптимального соотношения h к r для конуса с полусферой (рис. 2в), как мы это сделали для цилиндра (рис. 2а) и одиночного конуса (рис. 2в). Но тут символьная математика либо становится бессильной, либо выдает очень громоздкие решения. На рис. 2в задача о конусе, накрытом полусферой, решена «численной» функцией root для объема 10 м³. Ответ проверен на графике функции, которая была выведена символьной математикой Mathcad. Обсуждение этой задачи и ее аналитическое решение с помощью различных математических программ (Mathcad, Maple, Mathematica и Derive) можно посмотреть на форуме http://communities.ptc.com/message/197522.

Вопрос о том, нужно ли на занятиях по математике использовать реальные задачи или можно ограничиться абстрактными примерами, остается дискуссионным. Школьники начальных классов изучают азы математики (арифметики) на реальных примерах типа: «У вас в кармане два яблока. Некто взял у вас одно яблоко. Сколько у вас осталось яблок?». Затем, в старших классах и в вузе примеры постепенно заменяются на сугубо абстрактные – решить уравнение или систему уравнений, взять производную, найти первообразную и т.д. При этом «физика» задач напрочь игнорируется и мы еще это обсудим в конце статьи

В настоящее время, вернее, последние 30 – 40 лет,  в инженерном деле наблюдается повсеместный переход от аналитического решения задач к численным (их еще называют приближенными) методам. Это связано, с одной стороны, с громоздкостью и ограниченностью самих аналитических методов, а с другой – с развитием компьютерной техники. Лет тридцать назад какую-то конкретную задачу можно было решить только на уникальном компьютере вычислительного центра. Сегодня эту задачу можно решить на любом планшетнике или даже сотовом телефоне (смартфоне). Появились новые более сложные задачи, которые на планшетнике не решить, но можно послать через Интернет для решения на новом суперкомпьютере того же вычислительного центра. Но преподавание высшей математики в инженерном вузе, повторяем, по-прежнему базируется на учебниках трехсотлетней давности. Скажем не так категорично. Преподаватели высшей математики передают студентам знания, полученные самими преподавателями 30–40 лет назад, не просто игнорируя современные компьютерные средства, а убеждая всех, что они вредны для преподавания математики.

Мы здесь речь ведем об инженерных вузах, а не о «мехматах» университетов, где учат совсем другой математике. Многие, но, увы, далеко не все выпускники этих университетов успешно преподают математику в инженерных вузах, осваивая их профиль, вводя соответствующие примеры в читаемые курсы и используя компьютер. Но это, скорее, исключение, а не правило. Правило же такое – многие выпускники университетов читают в инженерных вузах просто укороченные университетские лекции по математике.

Третье событие, побудившее меня написать эту статью, касалось уже моих очных студентов, которым я также читаю курс информатики, базирующийся на использовании математических программ (см. http://twt.mpei.ac.ru/ochkov/Potoki.htm). На одной консультации перед экзаменом по информатике мои студенты признались, что они очень плохо сдали последний экзамен – экзамен по линейной алгебре, по учебному курсу, который студенты изучают параллельно курсам математического анализа и информатики. Ядром курса матанализа является изучение функциональных зависимостей, один из примеров которых дан на рис. 2. Линейная алгебра со своими векторами и матрицами нацелена на решение систем линейных алгебраических уравнений (СЛАУ). Анализируя провалы на экзамене (трудности понимания) моих студентов в линейной алгебре, я, иллюстрируя инструменты Mathcad, исследовал систему трех линейных уравнений и  привел для каждого случая геометрическую интерпретацию – см. рис. 3.

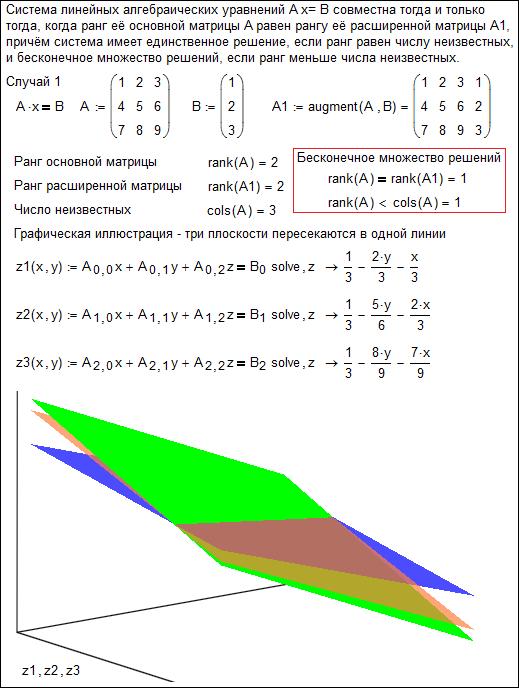
Рис. 3а. Решение СЛАУ в среде Mathcad – бесконечное множество решений

Примечание. Выражение rank(A)=rank(A1)=1 означает не то, что ранги матриц А и А1 равны единице, а то, что ранги этих матриц равны. В среде Mathcad единица (не ноль) в булевых выражениях это истина, а ноль – ложь.

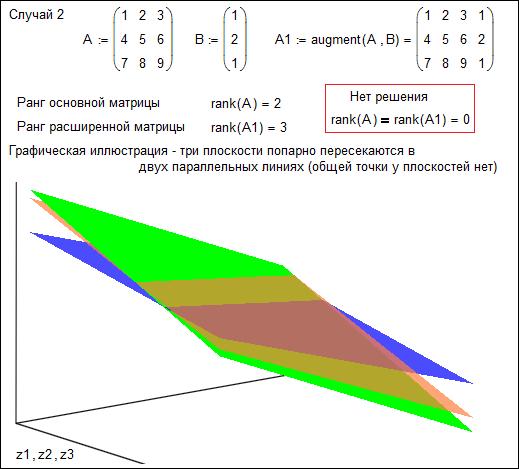
Рис. 3б. Решение СЛАУ в среде Mathcad – нет решения

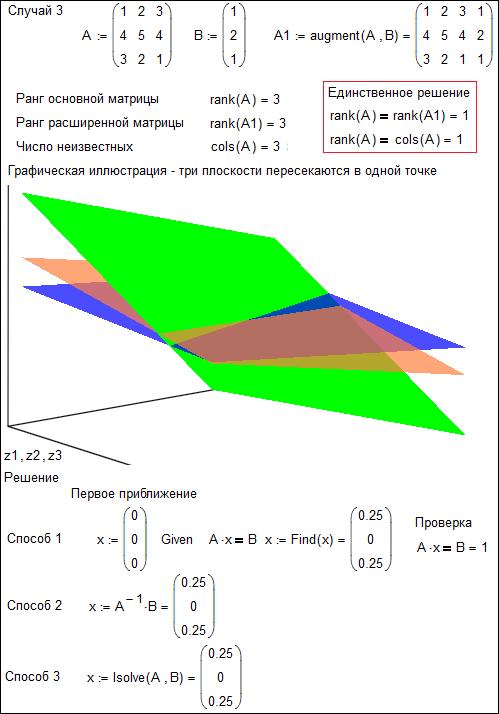
Рис. 3в. Решение СЛАУ в среде Mathcad – единственное решение

 

На рис. 3 средствами Mathcad показаны три случая, возникающих при решении систем трех и более линейных алгебраических уравнений: бесконечное число множество решений (три плоскости пересекаются не в точке, а на по прямой линии – рис. 3а), отсутствие решения (три плоскости попарно пересекаются на двух прямых – рис. 3б) и единственное решение (рис. 3в). После такого разбора задачи с ее графической интерпретацией студенты мне сказали, что если б им все это показали на занятиях по линейной алгебре, то они бы сдали экзамен намного лучше: не было бы простого зазубривания теорем, а было бы ясное понимание ну если бы не сути задачи, а как минимум ее постановки. Кстати, о решении СЛАУ в энергетике. Создание и реализация простейшей математической модели электрической сети отдельного населенного пункта или страны в целом – сводится к составление и решение СЛАУ с десятками или даже сотнями тысяч неизвестных. Без глубокого знания методов решения СЛАУ, то есть без знания линейной алгебры тут не обойтись. Системы большой размерности решаются численными методами линейной алгебры, изучение которых в стандартный курс линейной алгебры не входит.

Здесь тоже представляется весьма желательным и целесообразным решать задачи линейной алгебры на семинарах не «ручкой на бумаге», а «мышкой компьютера по его дисплею» или даже по большому экрану, висящему в аудитории, где читается курс линейной алгебры. Есть лазерные устройства, которые позволяют в аудитории над головами студентов построить плоскости, показанные на рис. 3.

Кстати, о визуализации решения, подкрепления его графиками и даже анимацией. Современные математические программы предоставляют пользователям простые и удобные средства анимации. На форуме PlanetPTC (РТС – это фирма-разработчик Mathcad) автор открыл подфорумы, на которых помещены анимации решения некоторых типовых задач математики – см. http://communities.ptc.com/groups/animation-of-math-methods-in-mathcad. На этом же форуме http://communities.ptc.com есть много трехмерных моделей, созданных в среде Creo (раньше эта система проектирования называлась PRO/Engineer) и рассчитанных в среде Mathcad.

Выводы:

1.      Современные математические компьютерные программы позволяют по-новому поставить преподавание математики в школе и вузе, учитывающее тягу школьников и студентов к компьютерам.

2.      Средствами графики и анимации можно существенно повысить понимание школьниками и студентами базовых понятий и теорем математики.

3.      Современные информационные технологии позволяют преобразовать традиционные решения математических задач в написание некоего реферата, где численные и аналитические решения будут дополнены рассуждениями об истории задачи, о развитии методов ее решения, о допустимости тех или иных ограничений и т.д. в стиле, например, данной статьи.

Продолжение данной статьи с дополнительными примерами можно найти на сайте http://twt.mpei.ac.ru/ochkov/Mathcad-15/OchkovMath.pdf.

Автор выражает глубокую благодарность Н.А. Сливиной [3] за ценные советы и замечания по статье.

Литература:

1.      Очков В.Ф. Открытое письмо пирата в адрес компьютерных изданий. Глава из книги «Mathcad PLUS 6.0 для студентов и инженеров». М.: КомпьютерПресс, 1996 http://twt.mpei.ac.ru/ochkov/mc8Pro.book/6_text.htm#_Toc525449695

2.      Очков В.Ф. Задачи по физике: новый подход к решению // Открытое образование, №6, 2012 г. http://twt.mpei.ac.ru/ochkov/Mathcad-15/Physic.pdf  

3.      Плис А.И., Сливина Н.А. Mathcad: математический практикум. Финансы и статистика. 1999.

4.      Очков В.Ф. Mathcad 14 для студентов и инженеров: русская версия. СПб.: BHV, 2009. http://twt.mpei.ac.ru/ochkov/Mathcad_14/RusIndex.html

5.      Д.Гурский, Е.Турбина. Mathcad для студентов и школьников. Популярный самоучитель. СПб.: Питер, 2005.

Послесловие

Есть такая книга, вернее, сборник «О математике: проблемы преподавания» (составители А.Д. Ярцева и А.В. Чернавский – М.: Знак, 2012 – 364 с. – см. www.ozon.ru/context/detail/id/19725947). Сборник очень неровный. Более половины текста сборника – это воспоминания о прекрасных педагогах-математиках и об уникальных школах и интернатах с математическим уклоном советских времен. Есть и другие очень интересные статьи, а есть явные спекуляции.

Основная идея книги («плач Ярославны») – такая: в СССР была лучшая в мире система математического образования, которую «демократы» и «либералы» постепенно разрушают.

Слов о том, что именно компьютеры помогают нашим «демократам» и «либералам» добивать «наше самое лучшее математическое образование», в явной форме в сборнике нет, но они в завуалированном виде пронизывают многие статьи. В частности, утверждается, что калькулятор и компьютер работают только с десятичными дробями, а начинать изучать математику (арифметику) нужно сугубо с простых дробей. Если этого не сделать, то никаких хороших знаний по математике школьникам уже не привить. Но современный школьник имеет под рукой калькулятор (см. начало статьи) и не понимает, зачем его заставляют учить эти самые простые дроби и в чем принципиальная разница между простой и десятичной дробью. Отсюда же идет и непонимание рационального и иррационального числа, алгебраического и трансцендентного уравнения и т.д. и т.п.

Что тут можно возразить, точнее, добавить?! Когда автор этих строк получал образование – среднее и высшее, дела обстояли так. Из десяти восьмых классов школы, где учился автор, в девятый класс перешло только 5 – 10%. Остальные шли работать на производство, поступили в техникумы или ПТУ. Через два года из десятого класса этой же школы в вузы поступало примерно 30% выпускников. Можно сказать, что в те годы, о которых ностальгируют авторы сборника (50-60-е годы прошлого столетия), старшие классы школы и вузы были элитными учебными заведениями, где посчастливилось учиться далеко не всем. А были еще и спецшколы и интернаты для одаренных детей, в частности, в области математики. Были также и «элитные» вузы типа МГУ (alma mater большинства авторов сборника), МФТИ, МИФИ… В эти вузы автор этих строк и не мечтал поступить. Теперь же в вузы, а точнее – в псевдовузы, которых сейчас расплодилось несметное количество, поступает 90% и более тех, кто десять-11 лет назад пошел в первый класс. О каком качественном математическом образовании тут может идти речь?! Нужно в десятки раз сокращать количество вузов, оставляя только те, где дают качественное высшее образование. А на это наше общество идти не готово и не пойдет.

И о дробях, простых и десятичных. Пакет Mathcad имеет средства работы с простыми дробями и при желании их можно успешно использовать в начальных классах школы. Основное действие при работе с простыми дробями, при их, например, сложении – это нахождение наибольшего общего делителя (НОД) знаменателей. В Mathcad есть такая функция – gcd. Кроме того, в среде Mathcad число можно с помощью оператора factor разложить на простые множители (69=3∙23 и 57=3∙19). На рис. П1 показано, как можно в полуавтоматическом режиме (цепочкой ручных присвоений, определив перед этим НОД и/или простые множители знаменателей) правильно сложить в среде Mathcad две простые дроби. (Кстати, в упомянутом сборнике в ряде статей с ехидцей констатируется, что американские школьники, решая такую задачу, просто-напросто сложат числители и знаменатели двух дробей и получат 181/126 и что скоро так будут делать все наши школьники, если не предпринять срочных мер по спасению математического образования).

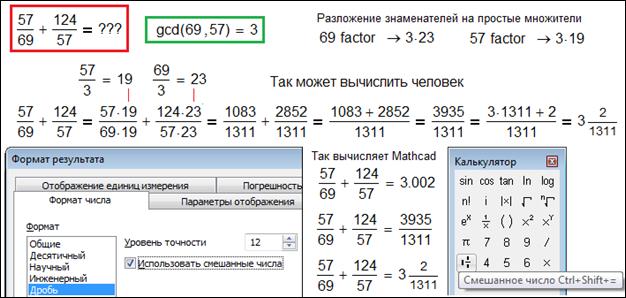
Рис. П1. Работа в среде Mathcad с простыми дробями

На рис. П1 показано также диалоговое окно форматирования результата, где есть позиция «Дробь», позволяющая выводить ответ в виде простой дроби. Этим инструментом, кстати, нужно пользоваться осторожно – можно вывести и отформатировать значение числа π в виде 22/7 и утверждать, что эта математическая константа является рациональным числом. На рис. П1 показана также панель операторов «Калькулятор», в котором есть кнопка ввода в расчет числа в виде целой части и части в виде простой дроби (смешанное число). Это позволяет очень продуктивно (и в смысле ответа и в смысле образования) работать с простыми дробями в среде Mathcad – вернуться, так сказать, в начальные классы школы.

Но есть в сборнике и зачаточные мысли о том, что компьютер при умном к нему подходе со стороны учеников, а главное, со стороны преподавателей может и возродить математическое образование – «я тебя погубил, я тебя и спасу!». В одной статье говорится об использовании на лекциях по математике компьютера, Интернета, проектора, большого экрана и т.д., но, увы, ничего не говорится о современных математических компьютерных пакетах, которые мы перечислили в самом начале статьи. Эту мысль мы и постарались развить в данной статье. Ведь преподаватели математики для многих школьников и студентов это не только «прекрасные педагоги», о которых много написано в сборнике, а также и «мучителей толпа», заставляющая заучивать теоремы и считать в уме. Многим людям до сих пор в кошмарных снах снятся наибольшие общие делители, наименьшие общие кратные, простые дроби и прочие «орудия пытки». Компьютер может на уроках математики взять на себя рутинную работу (убрать нудную сторону математики –  «орудия пытки»), оставляя учителю и ученикам простор для творчества.

И еще один аспект сборника, перекликающейся с темой статьи [2]. В сборнике много внимания уделяется анализу различий в подходах к решению задач физиками и математиками, вопросам привязки занятий по математике в вузах, вернее, во втузах к будущей инженерной специальности. Ведь студенты изучают математику не только для общего развития («гимнастика для ума» - см. начало статьи), но и для сугубо практических целей. Дискуссионный вопрос сборника – какие задачи решать на занятиях по математике: абстрактные или привязанные к профилю студента: электрика, теплотехника, химика и т.д. У автора в этом плане есть некая «красная тряпка», которой он дразнит математиков – найти корни уравнения x + x² = 0. Математики чувствуют подвох в этом вопросе и дают ответ (ноль и минус единица) только после дополнительных уговоров и разъяснений. Но когда они слышат, что нельзя складывать величину и ее квадрат, что это равносильно сложению метров с килограммами, математики тут просто взрываются. Другой пример (типовая задача математического анализа): есть функция (дан ее вид), требуется определить значения аргументов, при которых производная больше самой функции. Возражения в том плане, что это опять же «сложение метров с килограммами, вернее, расстояния и скорости», воспринимаются опять же в штыки. Математики очень болезненно реагируют на математические ошибки физиков, но очень легко прощают себе свои «физические ошибки», считая, и правильно считая, что математика совершенно свободна от реалий нашего физического мира. Из задачника в задачник кочует задача, которую списали еще с глиняных табличек древнего Вавилона (она приводится и в сборнике как иллюстрация того, откуда взялись квадратные уравнения – еще один кошмарный сон многих, но к счастью не всех бывших школьников): Я перемножил длину и ширину, получил площадь; излишек длины над шириной, сложенный с площадью, равен 183; сумма длины и ширины равна 27; найти длину, ширину и площадь. Вопрос о том, можно ли складывать длину («излишек длины над шириной») с площадью, математиков (и древних и современных) совершенно не волнует. На рис. П2 показано решение этой задачи в среде Mathcad.

Рис. П2. Задача о площади прямоугольника

Задача на рис. П2 решена – найдены два решения на выбор (в задачниках, как правило, приводится лишь одно решение), но перевод чисел a и b в размерные величины (длина) и проверка ответа (а ее всегда нужно делать при решении задачи и на компьютере и при ручном решении) выявила «физический» дефект задачи, о котором мы говорили выше. И таких задач в задачниках по математике уйма! Эти «авгиевы конюшни» нужно чистить! А Гераклом тут может выступить тот же компьютер, в паре, конечно, с математиками, ведущими занятия в школах и вузах. Им нужно прекратить наконец-то «плакать как Ярославна», а принять компьютер в «свои ряды». Мы должны наконец-то перестать мучить школьников и студентов работой, которую прекрасно может сделать компьютер и которую 99% школьников и студентов считают занудством, а только 1% математических талантов и гениев или просто одаренных людей – творческой работой. Нужны новые математические задачи и для развития «мозгов» и для практических целей. И задачи эти должны решаться в связке «человек – компьютер».

 

Приложение.

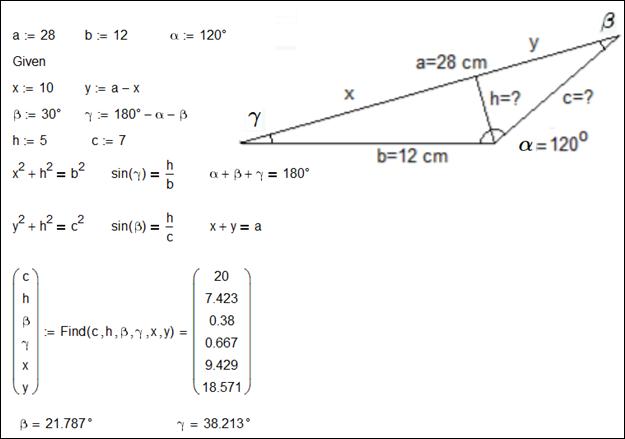
Еще одна школьная задача с решением на новый лад.

В треугольнике ABC сторона АВ имеет длину 6 м. Основание D высоты DC лежит на стороне АВ. Длина отрезка AD равна 4 м, длина стороны ВС равна 4 м. Найти длину высоты АЕ, которая опущена из вершины A на сторону ВС. Решение: