MAS на занятиях по математике, физике, информатике…

Журнал "Компьютерные учебные программы и инновации", № 2, 2006 г. (Другие статьи на данную тему >>>)

                             В.Очков (http://twt.mpei.ac.ru/ochkov)

В статье рассказано, как на уроках физики, математики, информатики можно использовать расчеты, открытые в Интернете, и как можно открывать свои собственные расчеты во Всемирной Паутине через технологию Mathcad Application Server (MAS)

Эпиграф

Диалог на занятии по компьютерному моделированию.

Студент: «Смотрите, как у меня на экране два тела ловко по орбитам крутятся!»

Преподаватель, молча глядя на дисплей: «Тут у тебя не два тела крутятся, а целых три - Исаак Ньютон в гробу тоже переворачивается...»

Начнем с «потревоженного» Ньютона.

Часто можно услышать такой риторический вопрос: «Как бы сейчас выглядело дифференциальное исчисление, если б у Ньютона был компьютер?!» У истории, как известно, не бывает сослагательного наклонения, но… Одни считают, что если бы у Ньютона был компьютер, то... никакого дифференциального исчисления не было бы. А было бы нагромождение решенных и якобы решенных задач, множество таблиц и кривых на дисплеях компьютеров, из которых какие-либо выводы, а тем более, общие законы сделать было бы чрезвычайно трудно – «голь (люди без компьютера) на выдумки хитра». Другие же утверждают в том плане, что «компьютеризированный Ньютон» помог бы нам избежать многих ошибок и заблуждений, уберег бы от поисков аналитических решений там, где их нет, и, в конце концов, привел бы к более бурному развитию науки и техники в целом и математики в частности. Но правильный ответ, наверно, таков: «Если б у Ньютона был компьютер, то это бы означало, что... дифференциальное исчисление как наука уже существовала в течение трехсот лет до Ньютона, а сам Ньютон (один из создателей дифференциального исчисления) носил бы другое имя...».

Все сказанное о дифференциальном исчислении можно отнести и к закону Всемирного Тяготения – второму великому детищу Великого и «некомпьюризированного» Ньютона, которому, как считается, этот закон "вошел в голову вместе с упавшим яблоком". Давайте посмотрим, как современные компьютеры могут помочь нам или наоборот помешать разобраться в одной известной физической задаче.

Pic. 1

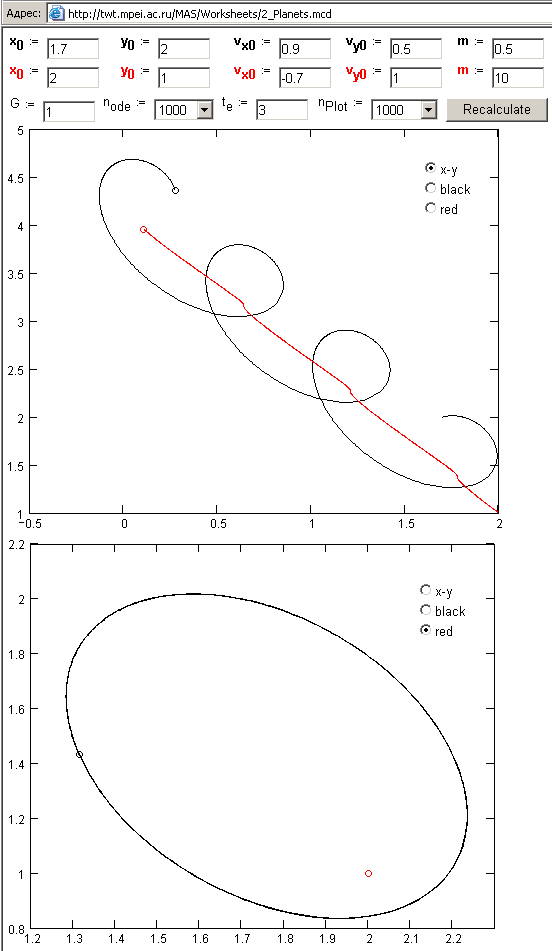
На рис. 1 показано решение в среде математической программы Mathcad задачи о вращении в безвоздушном пространстве (вернее, на плоскости) и в невесомости двух тел (см. эпиграф), «связанных» силой гравитации – спутника вокруг планеты, например. Задаются начальные параметры спутника и планеты (их массы, положение относительно начала координат и начальные скорости относительно двух координат). Далее решаются уравнения, связывающие две силы, действующие на тело – сила инерции (произведение массы на ускорение) и гравитационная сила, пропорциональная произведению масс спутника и планеты и обратно пропорциональная квадрату расстояния между ними. Коэффициент пропорциональности G – это гравитационная постоянная, значение которой также можно менять.

На рис. 1 вращение двух тел показано в двух системах координат: в координатах начальных условий (позиция «x-y» на радиокнопках) и в координатах, перемещающихся вместе с красной планетой («red» – наблюдатель находится на этой планете). Можно построить график относительно и черной планеты («black»), но характер орбиты не изменится – она останется эллиптической. Задача о двух планетах на MAS >>>.

Pic. 2

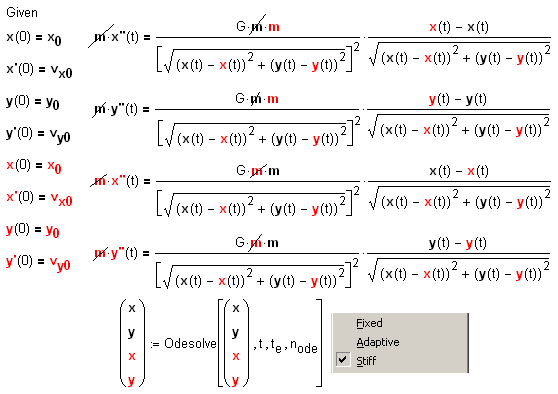
На рис. 2 показаны операторы Mathcad, решающие задачу – формирующие пользовательские функции, по которым строятся орбиты планет. Операторы «раскладывают» по осям x и y второй закон Ньютона a•m=F и закон всемирного тяготения G•m•m/r², где r – это расстояние между двумя телами. У нас одно из них черное, а другое – красное: среда Mathcad допускает окрашивание переменных, что очень удобно и уместно, если затем характер этих переменных и функций иллюстрируется цветными графиками[1], как в нашем случае. Второе удобство Mathcad при решении уравнений движения – это возможность работы со штрихом (первая производная пути – скорость) и двумя штрихами (вторая производная – ускорение). Читатель может заметить, что в уравнениях, показанных на рис. 2, корень возводится во вторую степень (?!), а переменные m находятся в левых и правых частях уравнения и могут быть сокращены. Но здесь пакет Mathcad считает по оптимизированным (упрощенным, профилированным, как скажет программист) формулам, а пользователю «показывает» исходные, неупрощенные формулы, в которых «физика» задачи ясно видна.

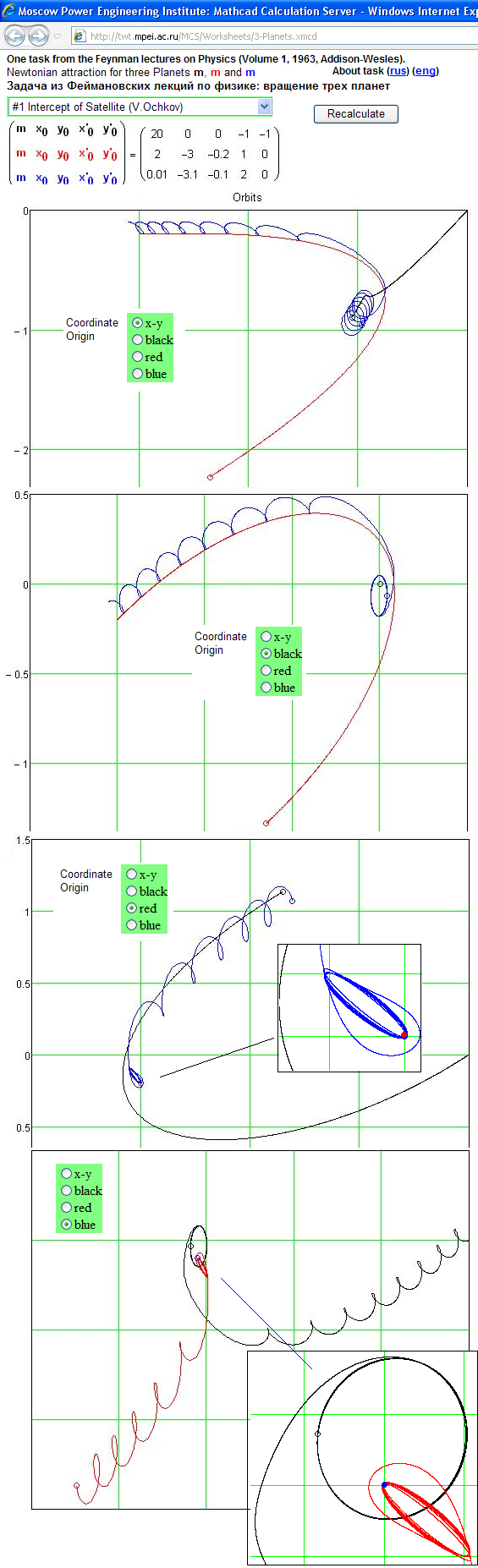
Если же нашу систему расширить до 6 уравнений и ввести дополнительные исходные данные, то можно решить задачу о трех вращающихся на орбитах телах – см. рис. 3.  Задача о трех планетах на MAS >>>.

Pic. 3

Пакет Mathcad хорошо известен многим школьникам, студентам, инженерам, преподавателями. Выпущено большое количество литературы по этой компьютерной программе (см. http://www.exponenta.ru/soft/Mathcad/mathcad_book.asp), содержащей множество задач с решениями, подобным тем, какие мы показали на рис. 1 и рис. 3. Новое здесь в том, что наши задачи можно решать не на собственном (персональном) компьютере, а во Всемирной Паутине – в Интернете. Об этом свидетельствует обрамление рис. 1 и рис. 3 – см. их заголовки с адресами расчетов в строке браузера Internet Explorer. Такой удаленный доступ к расчетам в среде Mathcad ведется по технологии Mathcad Application Server (MAS), когда на сервере Интернета можно открыть документ с расчетом, изменить исходные данные, нажать на кнопку «Recalculate-Пересчитать» и получить новый ответ – числа, графики, рисунки… При этом пользователь может вводить не только свои индивидуальные данные и получать новые орбиты.

Встроенная в Mathcad функция Odesolve (см. рис. 2) , предназначенная для решения (solve) обыкновенных дифференциальных уравнений (ode – ordinary differential equations), «разделала» нашу задачу численно: маленькими шажками (их число задается переменной t_ode) рассчитываются координаты планет за период времени от нуля до 3 (рис. 1) или до 1.5 (рис. 3) условных единиц (переменная t_e). Но еще со времен Ньютона и Галилея было известно и аналитическое решение задачи о двух телах – они вращаются по эллиптическим орбитам и мы об этом уже упоминали – см. второй график на рис. 1. С тех же времен не прекращались попытки аналитического решения задачи о трех вращающихся телах, пока не было доказано, что этого сделать нельзя, а нужно опять же «маленькими шажками» просчитывать орбиты планет, т.е. решать задачу численно: необходимо рассчитывать текущие координаты планет при заданных начальных условиях, а не по готовым формулам, описывающим траектории орбит. В наше «компьютерное» время это стало делать намного проще («Ах, как жаль, что у Ньютона не было компьютера! Он, бедный, все считал на бумаге!»).

На рис. 3 начальные условия были подобраны так, чтобы был смоделирован довольно интересный случай, когда одна планета у другой «отнимает» спутник.

Первую часть названия статьи (MAS) мы расшифровали, поговорим подробнее о второй части названия – о школьный или вузовских занятиях…

В настоящее время все больше и больше классов и аудиторий оснащаются мультимедийными компьютерными проекторами, позволяющими выводить на большой экран в том числе и страницы Интернета. Технология MAS дает возможность демонстрировать таким образом и расчеты, подкреплять ими, например, реальные физические опыты. Вращение планет в физическом кабинете показать нельзя, а вот законы трения, качания маятника, соударения тел и многого другого – можно. Математические модели этих и многих других явлений, реализованные в среде Mathcad, можно найти на сайте www.vpu.ru/mas (см. рис. 4) в разделе Разное.

Pic. 4

MAS пригодиться не только на занятиях по физике, но и математике или информатике?! Если на уроке математики MAS поможет строить графики и поверхности, решать уравнение и системы, то на занятиях по информатике, в частности, можно рассказать, какая программа с циклами и альтернативами скрывается за функцией Odesolve (cм. рис. 2), позволившей нам так просто, быстро и изящно реализовать довольно-таки сложную физическую модель. Можно дополнительно показать, какие алгоритмы заложены в эту функцию и как они могут влиять на решение задач. Функцию Odesolve можно настроить на три метода решения дифференциальных уравнений:

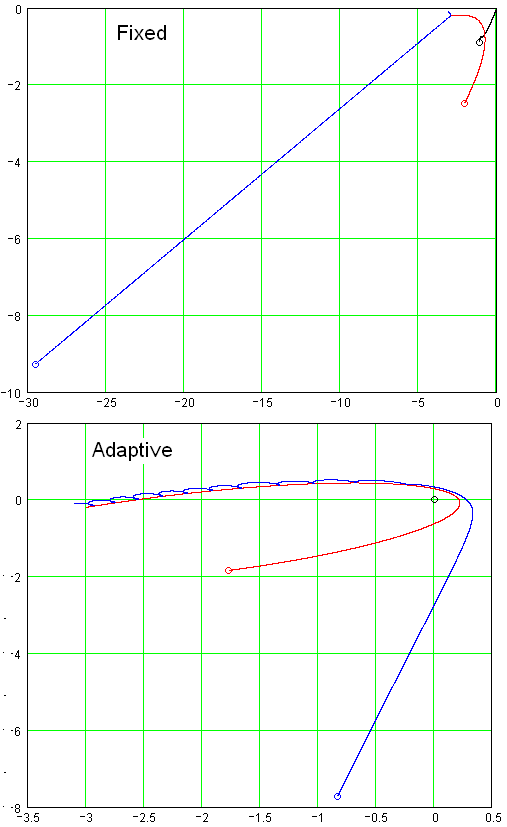
·        Fixed – расчет с фиксированным шагом;

·        Adaptive – расчет с переменным (адаптивным, подстраивающимися) шагом, когда на более-менее линейных участках шаг увеличивается, а на «крутых» – уменьшается;

·        Stiff – расчет так называемой жесткой системы, когда каждое уравнение требуют индивидуального шага.

На рис. 3 перехват спутника был просчитан через функцию Odesolve, настроенную на решение жестких систем дифференциальных уравнений (Stiff). Но если бы был применен алгоритм Fixed или Adaptive, то спутник не был бы перехвачен – он был бы просто сбит с орбиты, что зафиксировано на рис. 5. Ахиллесова пята численных методов – накапливающаяся ошибка вычислений, способная не просто исказить ответ, а сделать его неузнаваемым (пресловутый переход количества в качество). Одно дело – на лету, пользуясь телеметрической информацией, подправить предварительно рассчитанную траекторию полета космического зонда к Марсу, например, а другое дело – пролететь мимо красной планеты... Можно спросить, как же тогда космические корабли, покидая Землю, оказываются в нужной точке Мирового пространства?! Дело в том, что траектории их полета предварительно просчитываются, а затем корректируются с учетом реального положения.

Pic.5

Когда говорят, что кто-то «переворачивается в гробу» (см. эпиграф), то имеют в виду, что некий классик[2] недоволен, когда к его творению прикасаются «очумелыми ручками». Траектории смены орбиты (см. рис. 3) довольно занимательные и поучительные, но соответствуют ли они действительности либо точному (аналитическому) решению задачи, если оно существовало бы...

Какие из трех форм орбит, показанные на рис. 3 и рис. 5, более близки к истине?! Тут нужно сравнивать их с аналитическими решениями, а их нет. С либо с реальным положением «звезд на небе»…

На сайтах http://twt.mpei.ac.ru/mas/worksheets/Euler.mcd и http://twt.mpei.ac.ru/mas/worksheets/rkadapt.mcd (см. рис. 4) можно найти графическую иллюстрацию различий в методах решения дифференциальных уравнений (простейший метод Эйлера, методы Рунге-Кутта с фиксированным и переменным шагом), а на сайтах http://twt.mpei.ac.ru/mas/worksheets/Rectangle_Int.mcd и http://twt.mpei.ac.ru/mas/worksheets/Trapezium_Int.mcd – «графические сущности» разных методов интегрирования – метода прямоугольников и трапеций.

Повторяем, открыв сайты, показанные на рис. 1 и рис. 3, – на персональном компьютере или на большом экране аудитории (классной комнаты), можно, «поиграв исходными данными», получить более интересные траектории – траектории, например, Солнца, Земли и Луны: эллипс, точки которого обвиты другими эллипсами… Можно перейти от плоскости к объему, от трех планет к четырем и так далее (см. http://www.santafe.edu/~moore/gallery.html, например). Можно учитывать непостоянства во времени величины G[3]. Можно также учитывать непостоянство величины G и в пространстве. Тут придется перейти от решения обыкновенных дифференциальных уравнений к решению дифференциальных уравнений в частных производных – производных по времени и по пространству. Можно планетам задавать не только массы, но и диаметры и учитывать их соударения. А вот еще интересная задача – пролетит ли некий астероид мимо планеты либо врежется в нее (интрига многих фантастических романов и фильмов). Можно смоделировать включение на спутнике в какой-то момент двигателя и смотреть, как изменится его орбита… Если на компьютере преподавателя или ученика установлен пакет Mathcad, то можно скачать сами файлы, отображенные на рис. 1 и рис. 3, и доработать их самому…

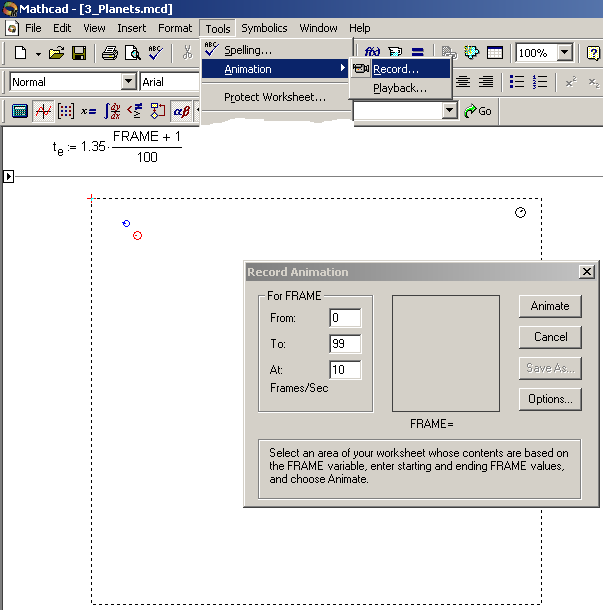
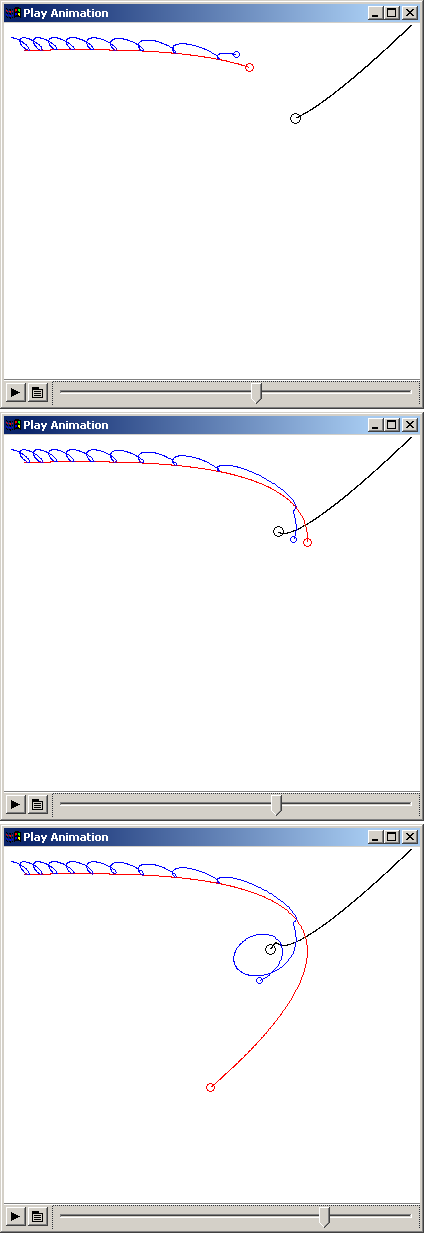
В среде Mathcad есть очень удобные средства анимации. Рассчитанную траекторию планет можно отобразить не только на статичных графиках (см. рис. 1, рис. 3 и рис. 5), но и в движении. Его можно проследить, плавно меняя значение переменной t_e от положительного значения, близкого к нулю (старт планет), до конечного значения, показанного на рис. 1 (3) и рис. 3 (1.5 – окончание полета). Но анимации при этом не будет – она получается при смене кадров не менее десяти в секунду. Можно ускорить этот процесс, перелистывая кадры, хранящиеся в буфере браузера Internet, но лучше эту работу поручить самому пакету Mathcad с его встроенными средствами анимации. На рис. 6 показано диалоговое окно создания анимации в среде Mathcad, когда пользователь через системную переменную FRAME формирует 100 кадров анимации, отображающих положения планет при дискретных значениях переменной t_e. Эти кадры затем можно просматривать с заданной скоростью (10 кадров в секунду – см. рис. 6) и без Mathcad – через видеоплеер Windows, например – см. рис. 7, где зафиксированы три фазы перехвата спутника.

Pic. 6

Pic. 7

Литература:

1.                   Очков В.Ф. Mathcad: от графика к формуле, от расчета на компьютере к расчету в Интернет» // Exponenta Pro, Математика в приложениях», 2003, № 4 (http://twt.mpei.ac.ru/ochkov/Plot_Spline).

2.                   Очков В.Ф. Математические пакеты: От натурального хозяйства к товарному производству через Интернет // КомпьютерПресс, 2004, №5 (http://twt.mpei.ac.ru/ochkov/MAS_KP/mas_kp.html)

3.                   Очков В.Ф. О кнопке Submit из набора WebControls пакета Mathcad или Сетевая и несетевая псевдоанимация в среде Mathcad // Exponenta Pro, Математика в приложениях», 2004, № 1 (http://twt.mpei.ac.ru/ochkov/VPU_Book_New/mas/From_WorkSheet_to_WebSheet.html#3)

4.                   Очков В.Ф. Развитие интерфейса Mathcad: от DOS к Internet // Exponenta Pro, Математика в приложениях», 2004, № 7-8 (http://twt.mpei.ac.ru/ochkov/Interface_Mathcad/index.html)

5.                   Очков В.Ф. Mathcad 12 для студентов и инженеров. БХВ-Петербург, 2005 г. (http://twt.mpei.ac.ru/ochkov/Mathcad_12)

6.                   Очков В.Ф. Теплотехнический справочник в Интернете // Новое в российской электроэнергетике, №5, 2005 г (http://twt.mpei.ac.ru/ochkov/VPU_Book_New/mas/NRE_5_5/index..html).

7.                   Очков В.Ф. MA и MAS: проблемы и решения при создании web-ресурсов сферы образования. Вопросы Интернет Образования, № 29 (http://vio.fio.ru/vio_29/cd_site/Articles/art_1_12.htm)

 

Родственный сайт - http://www.ifmo.ru/butikov/Projects/CollectionR1.html

Данная работа выполнена с поддержкой коллег по Collaboratory (http://collab.mathsoft.com/~mathcad2000). См. рис. ниже: