В. Ф. Очков, Е. П. Богомолова,
Национальный исследовательский университет МЭИ, Москва
Рекурсия
Германн сошёл с ума. Он сидит в Обуховской больнице в 17-м нумере, не отвечает ни на какие вопросы и бормочет необыкновенно скоро: «Тройка, семёрка, туз! Тройка, семёрка, дама!..»
А.С. Пушкин «Пиковая дама»
Почти
все знают, что такое факториал числа – n!. Это произведение всех натуральных
чисел от 1 до n включительно: 5! = 1
2345 = 120, например. Такое
классическое определение факториала не охватывает нуль. Но факториал нуля легко
подсчитать (не определить, а, именно подсчитать) с помощью рекурсии. Вот как
определяет рекурсию один юмористический справочник по информатике: “Рекурсия –
см. рекурсия”. Рекурсивное определение функции подразумевает то, что эта
функция вызывает сама себя. На рисунке 1 помещена программа-функция для Mathсad Prime подсчета факториала с
использованием рекурсии.
Рис. 1. Рекурсивная функция “Факториал”
Словесное
описание этой функции такое. Если n
равно 5, то n! равен 120 (см. первые две
строки программы на рис. 1). Если n
больше 5, то
факториал такого целого числа равен (n
– 1)! ∙ n. Пример 6! = 5!
6 = 720. Если n меньше 5, то n! равен (n + 1)!/(n
+ 1). Примеры: 4! = 5!/5 = 24, 3! = 4!/4 = 6, 2! = 3!/3 = 2, 1! = 2!/2 = 1 и,
наконец, 0! = 1!/1 = 1, что и требовалось доказать.
В Интернете есть очень интересный сайт http://oeis.org «Открытая энциклопедия целочисленных последовательностей». Если в окошко этого сайта ввести последовательность чисел 1, 1, 2, 6, 24, 120, 720 (см. выше) и нажать кнопку Search (Искать), то сайт выдаст ответ, что это факториал, и будет много рассказано интересного об этом математическом операторе.
Очень забавно вводить на этом сайте различные последовательности целых чисел и узнавать, какой закономерности они подчиняются. Так, например, если ввести числа 1, 2, 3, 5, 8, 13, 21, то будет получен ответ, что это числа Фибоначчи – числовой ряд, где каждое очередное число – это сумма двух предыдущих чисел – см. рис. 2.
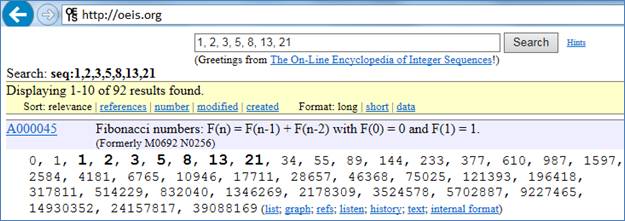
Рис. 2. Сайт определения закономерностей в целочисленных последовательностях
Интересно найти закономерность той или иной числовой последовательности самому или с помощью сайта, показанного на рис. 2. Но еще интересней “утереть нос” этому сайту – ввести числовую последовательность с известной закономерностью и увидеть, что сайт дал слабину и не нашел ответа. После этого можно будет зарегистрироваться на этом сайте и ввести в него новую информацию. Попробуем это сделать. Что такое числа Фибоначчи (см. выше), знают многие. А вот что такое прекрасные числа Фибоначчи, мало кто знает. “Красивые” числа – это 1, 3 и 7. Если их сложить, то получится еще одно “симпатичное” число – 11. Вспомним: “Тройка, семерка, туз (11)!” На рисунке 3 показана рекурсивная функция, возвращающая прекрасные числа Фибоначчи не только при положительном, но и при отрицательном аргументе. В этой более полной последовательности чисел появилась и пятерка, которой также нельзя отказать в “изящности”, если вспомнить школьные и институтские оценки знаний.
Рис. 3. Прекрасные числа Фибоначчи
Так вот, если в окошко упомянутого сайта (рис. 2) ввести числа 1, 3, 7, 11, 21, 39, то он “раскусит” эту последовательность, отметив, что каждое очередное число – это сумма трех (а не двух – см. рис. 2), предыдущих. Но если этому сайту оказать “медвежью услугу” – расширить ряд до -1, 3, 1, 3, 7, 11, 21, 39 (приписать в начале последовательности чисел минус 1 и тройку), то ответа не последует – “каша будет испорчена маслом”.
Предлагаем читателям “поиграть” с сайтом oeis.org, вводя в него числовые последовательности, созданные программированием (см. рис. 1 и 3) или с опорой на свою собственную смекалку. Сайт oeis.org, к примеру, знает, что 1, 2, 5, 10, 20, 50 и 100 – это номиналы банкнот США, а 5, 10, 20, 50, 100, 200, 500 – это банкноты евро, и прогнозирует будущие банкноты в случае гиперинфляции. Но этот сайт не знает, что 1, 2, 3, 5, 10, 25, 50, 100 – это номиналы банкнот бывшего СССР[1]. Неизвестно сайту также и то, что 7, 9, 11, 13, 15, 19, 22, 28, 48 – это стоимость (в копейках) мороженного в том же бывшем Советском Союзе. В программе, показанной на рисунке 3, можно поменять опорные числа («тройку, семёрку, туза» на «тройку, семёрку, даму (еще одну тройку – см. эпиграф), получить новую последовательность целых чисел и пропустить ее через сито сайта oeis.org.
Но вернемся к нашей основной теме – к рекурсии.
Расчет факториала (рис. 1) и чисел Фибоначчи (обычных или прекрасных) можно вести и без рекурсии – с помощью, например, рекуррентной формулы: знаешь предыдущие числа – высчитываешь очередное, очередное становится одним из предыдущих, а сама операция продолжается до тех пор, пока не доберемся до искомого числа. Такой счет ведется быстрее и не требует значительных ресурсов памяти компьютера. Но рекурсия очень упрощает написание программы. Классический пример – программа, решающая головоломку “Ханойской башни”.
Рис. 4. Ханойская башня с рекурсией
Суть головоломки. Имеется три стержня, на первый из которых (у нас в программе на рис. 4 он маркирован как A) нанизаны диски на манер детской пирамидки: самый большой диск внизу – самый маленький наверху. Предлагается переложить эти диски на стержень C, беря их по одному и не кладя большой диск на маленький. Для временного складирования разрешается использовать третий диск B. Программе на рис. 4 достаточно сообщить только число дисков в пирамиде n. После запуска программа будет возвращать порядок перекладки дисков:
n=2: AB, AC и BC (три хода)
n=3: AC, AB, CB, AС, ВA, BC и, наконец, AC (семь ходов)
n=4: … (15 ходов) и т.д.
Число перестановок p в общем случае равно 2n-1. Задача с n дисками легко сводится к задаче с n-1 дисками, а задача с n-1 дисками легко сводится к задаче с n-2 дисками и т.д. до задачи с двумя дисками, которая решается просто – диск со стержня A перекладываем на диск C (см. на рис. 4 фрагмент программы If n = 1…). Отсюда и рекурсия в программе на рис 4.
По древней легенде тибетские монахи уже несколько тысячелетий перекладывают 64 золотых диска, нанизывая их на алмазные стержни. Когда головоломка будет решена и на стержне C окажутся все диски, наступит конец света. Спасает нас лишь то, что при 64 дисках для решения головоломки потребуются свыше… триллиона лет, если на каждый ход тратить по секунде. Это без учета ложных ходов и времени, необходимого на ручной или компьютерный расчет порядка перестановки дисков. В Интернете, кстати, есть виртуальные игры «Ханойская башня». Откройте ее и поиграйте с 5-10 дисками.