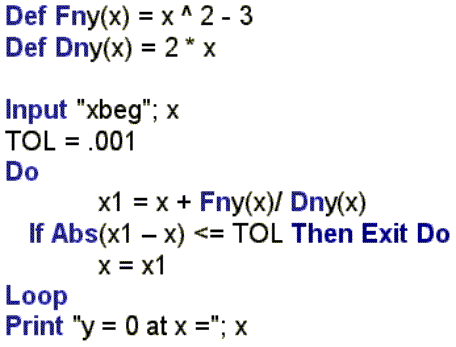6.7. Remake (about main structural constructions of Programming)
Author
will tell you about peculiarities of Mathcad as a remake in his seventh part of
the etude.
Why is
it the remake? At first we have to look through the preface. For the second
file with the text «Turbo
Pascal 7.0. View from the side» (Computer
Press, ¹ 7’93) is kept. This article is the remake. For the third in
Mathcad, like in Pascal, there are some aged dogmas[1] of structural programming. This article was written about it. All these
things make our remake simple, useful and natural.
So,
it is the remake.
We
try to show on simple examples that enter in Mathcad of the operators break, continue and return (see above) is only one
step for increasing the
flexibility of control designs of this programming language.
Picture 6.16. The Newton method I (BASIC): cycle with middle escaping
At
the picture 6.16 there is BASIC-program for finding the root of an algebraic equation by the Newton method
(tangents). Why do we begin from BASIC, but our etude is devoted
programming language Mathcad? BASIC has universal cycle with middle escaping: Do [...] If ...
Then [...] Exit Do [...] Loop, .besides traditional cycles
(cycle with preliminary control, cycle with subsequent control, cycle with parameter).This design
allows to realize algorithms with natural sequence. About other advantages of
this design we will tell later. This way at the picture
6.16 the functions of user are declared (we analyze the equation y and its derivative dy), then the value of started
approximation of x is asked, and the value of an error TOL. is
declared. After it we make the cycle with the middle escaping, but not
traditional one. In this cycle, following natural order of the Newton method,
new approximate value of the root (x1) is calculated. If this
value does not differ from previous one more than the value of the given error[2], (Then) it is considered the problem is solved (Exit Do). Otherwise we prepare next approximation (x = x1),
but the cycle repairs (Loop).
In
Mathcad this simple algorithm gets « architectural
extravagances », as since this algorithm is realized by the function and is «packed» to
the cycle while. See the picture 6.17.
The picture 6.17. The Newton method II: cycle with preliminary control
The
cycle with preliminary control (the cycle while)
requires that Boolean
expression of heading was determined before entering the cycle. But it does not
take place finding the root by the Newton method. We have to write before
entrance the cycle (and for entrance) x1 ¬ x + 2 × TOL. This way someone lies
children (but a computer is like a child), making them to do something. Line x1 ¬ x + 2 × TOL is
like a starter of an
internal-combustion engine, working cyclically. See the picture 6.17. We get a lot of
difficulties in such simple problem because in Mathcad there is no cycle with
middle escaping. At the picture
6.17 we can notice one more problem in this program: we put a cart at the front of the horse.
At first in the cycle we prepare for new approximate (x1 ¬ x), though we do not know if we need it, but only then we enter the
cycle.
The
operators break, continue and return, gated in Mathcad, have to turn back the
program at the picture 6.17 its naturalness, but...
The picture 6.18. The Newton method III: Imitation of the cycle with middle escaping (Cycle WHILE)
BASIC
is the design. Do ... Loop (see the picture 6.16) at the picture 6.18 becomes the design
while 1 ...,which can be translated into Latin as «ad
calendas greaces». Here, like in the program at the picture 6.17, we have to go on a strained interpretation.
Operator
continue differs from operator break, that
this operator turns over
control to the beginning of the cycle[3]. But documentation and help files of Mathcad do not have any examples, justifying using operator continue. Author cannot think out them too.
The
history about input in Mathcad the operators break and
continue and return confirms aged true, that « there is nothing more
practical, than the good theory ».
Above-mentioned
analysis of cycles in Mathcad has both practical and idealized aspect. It is
well known that the any set of
control designs of any structural language conducts parentage from the basic
structural theorem W. Dijkstra. This theorem disclaims any labels: «The
algorithm of any difficult we can realized using only the cycle while and alternative ». Author spent a lot of time for proving this theorem in his articles
and books, but he did not find anything. But to show that this theorem is not
truth we can easily (see the pictures
6.19 and 6.20). These programs solve well-known problem about the root of
the algebraic equation. But they do it another method. It is the method of half
division. The algorithm of this method is simple illustration of the theorem W.
Dijkstra: the cycle (while) is the approximation to
the root, where there is alternative (if ... ). If the root is on the
right the middle of the interval a-b, then left limit comes
nearer (the center) (a ¬ x), otherwise (b ¬ õ).
The picture 6.19. The method of half division I (Mathcad)
In
the program at the picture 6.20 the alternative of the program at the picture
6.19 is changed by two cycles while. The operators are executed
once or never, that is regulated
by the Boolean variable Flag.
The picture 6.20. The method of half division II (Mathcad)
Besides
in the program at the picture 6.20 the cleaning of a cycle is conducted. In the body of this cycle
the value of an analyzed function is calculated only once. In the program at
the picture 6.19 it was done two times. The second change in the program at the
picture 6.21 against the program at the picture 6.19 is we do not use
the function Heaviside. The letter Ô is not Greek letter «ôè», but
it is Russian letter «ýô» and one does a mistake. This mistake is found
out very difficult, that is why it is difficult corrected. The function Heaviside
changes the multiplication of values of the analyzed functions on the limits.
Boolean operation And in the program at the picture 6.20 is not
called as the function And(...,
...), but the tree-type operator.
The picture 6.21. The method of half division III (QBasic) (blue – the loop, green – alternative)
In
similarly BASIC-program (at the picture 6.21 it is put
in the structural diagram) we do not use alternative. Moreover, we do not use
the variable Flag, changed two cycles while by
one cycle. But this cycle is with two middle escaping. One of them is
conditional escaping, the other is unconditional one.
Locus
of the programs at the pictures 6.20 and 6.21 is the alternative. It is the
means of accelerated «trip» through the algorithm only to the one direction (top-down and from left to right),
but the cycle is a “trip” to two directions. So, we see the alternative is
useless (but it only theory, and this alternative is useful in practical aspect[4]). The cycle Do [...] If ... Then [...] Exit Do [...] Loop we
can consider an hybrid of the cycle and the alternative.
The
proof of the theorem W. Dijkstra we can consider that there are no cases, the
planned algorithm one can not realize, using only the cycle and the alternative[5]. If the alternative is excluded, then the main structural theorem is: «Algorithm any complexity one can realize, using only
the cycle». This theory of input of the operators break, continue and return requires programming language Mathcad. It is
the base of Mathcad. The cycle with middle escaping in Mathcad we execute through violence above
the cycle while (the picture 6.18). Also we have to write in
the title of the cycle some trivial
true: «Volga runs into the Caspian sea».
The
theorem W. Dijkstra we have «to
lower in a rank» and to call as a lemma, that is auxiliary theorem, that
serves for proving the main theorem.
Here we come back to disputes, that took place 30 years ago. The operators
break, continue and return, gated in Mathcad, gave us reason to remind about them. These operators
have reconciled the supporters
and opponents of the GOTO statement to a label.