Translation by I.Repkin.
Dear readers!
Please send your corrections on grammar and spelling of the text by e-mail: Pat33@mail.ru.
Sincerely yours Ilya Repkin.
Painting and sculpture in Mathcad
A black circle in the black square
Fig. 1.
Computation of number p by
the Monte-Carlo method
The volume of a cone, or Pointiller
Fig. 2.
Calculation of the volume of a cone
A
black circle in the black square
In precomputer era only a few afflicted with some idea people (derivators of a sort) dared to conduct calculations by algorithms which are now easily solved with a computer at hand. It is known from literature that a French naturalist G. de Buffon (XVIII century) had thrown a coin 4040 times and had calculated heads to turn out 2048 times, and tails – 1992 times. An English statistician K. Pearson had described series of 12 000 and 24 000 coin-tossings. In the first case heads had turned out 6019 times and in the second one – 12 013 times.
The same Buffon had
chosen a very interesting way to derive number p: he had drawn parallel
equidistant straight lines on
a sheet of paper and had started casting a needle of length equal to an
interval between the lines on this sheet in a random way. He had calculated a
total number of castings (N) and a number of needle hits upon one of the lines (n). The probability theory suggests the ratio n/N to embody number p Buffon had tried to determine in a such
unusual way.
For example, a definite integral value is possible to be estimated by statistical tests (or by the Monte-Carlo method, that is another name of calculation methods applied by Buffon and Pearson) in the following way. One needs to inscribe a graph of an integrable function into a rectangle and to fling in a random way … pebbles at it. Kozma Prutkov recommended in a similar situation, but when pebbles were flung into water, to look at ripples in the water for, otherwise, such occupation becomes an idle pastime. Let's take advantage of the advice, but we shall compute not ripples but amount of pebble hits upon a graph. Ratio between a number of hits (n) and a total number of castings (N) should hold a value of the integral if the probability theory to be trusted.
So, we start throwing «pebbles into the water».
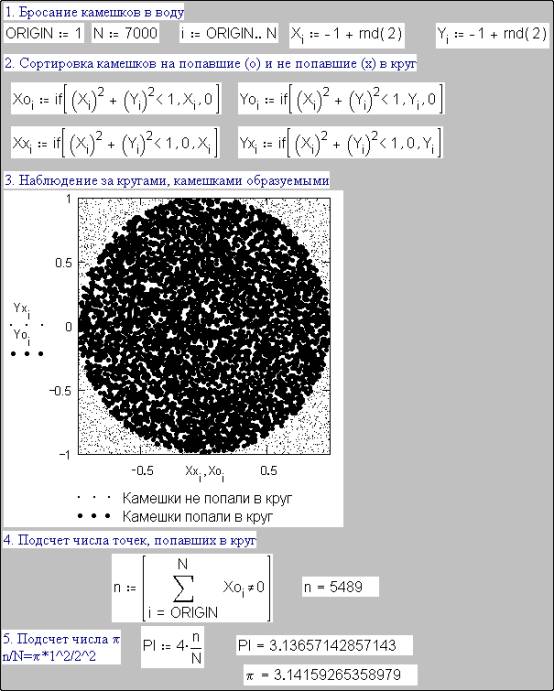
Fig. 1. Computation of number p by the Monte-Carlo method
1. Casting pebbles into the water
2. Sorting pebbles to having hit the circle (o) and not having hit it (x)
3. Observation of ripples in the water
Pebbles had hit the circle
Pebbles had not hit the circle
4. Computation of a number of points which had hit the circle
5. Computation of number p
There is a less sophisticated method of a number p statistical calculation as compared to the one applied by Buffon. A square should be drawn, a circle should be inscribed into the square («squaring the circle») and it remains to throw pebbles there. Since area of a circle keeps number p («pi times ar squared» – we shall recollect an old joke: why do train wheels hammer?), calculation of a number of hits upon the circle allows estimation of number p. Buffon did not use this technique for probably it was difficult to secure a regular pebble hitting upon the square.
Fig. 1 displays estimation of area of the circle inscribed into the square and illustrates an attempt to calculate the value of number p. How did we do it?
Item 1 on Fig. 1 demonstrates creation of two vectors X and Y, which elements (there are 7000 elements) – are random real numbers in the range from minus unit to unit. X and Y – are properly coordinates of points of pebble random hits upon the square of size 2 by 2. Then in item 2 these pebbles are sorted to «pure and impure»: coordinates of points which had hit the circle are recorded in the vectors Xo and Yo (o – hit), and coordinates of points which had not hit the circle – in the vectors Xx and Yx (x – miss). After that it becomes foolproof to visualize point hits upon the circle by means of a parametric Cartesian diagram. It will suffice to specify absence of lines and presence of points on the diagram while formatting it. Points which had hit the circle (vectors Xo and Yo) therewith are more thick. Now a number of pebble hits upon the circle should be calculated in order to estimate number p (item 4) – that is a number of nonzero elements of the vector Xo (or Yo). Item 5 presents calculation of the value of number p and its comparison with the precise value.
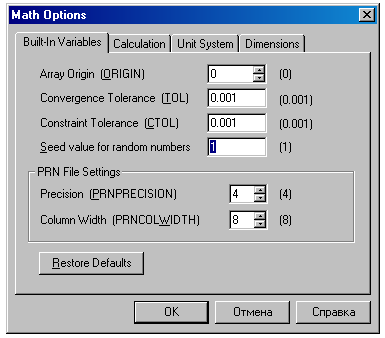
The function rnd in the Mathcad environment has an argument varying from its analogs from programming languages. In the BASIC or Pascal environment the argument of the rnd function is associated with the prefix pseudo- in its name, rather than with a range of random numbers generated. Yes, numbers are generated in a random way, but a sequence of these numbers is pseudorandom, for it can be reconstructed at any time. In programming languages the argument of the function rnd is charged with such reconstruction, and in the Mathcad environment a number (by default it is 1) is responsible for that. The number is stored in the window «Seed value for random numbers» (initialization of the generator of random numbers) of the shortcut «Built-in Variables» of the window «Math Options», displayed by the command «Options» from the menu «Math»:
True random numbers were rejected as far back as the earliest stage of computer
development when programmers were trying to build into computer something like a roulette. But the device appeared
rather clumsy and the main disadvantage was that it did not allow iterative
series of random (pseudorandom) numbers required at a program debugging. That is why mathematical
simulation is favored over random number generation by means of physical
analogs (a roulette). A user little cares of an algorithm the function rnd is based on – the main thing is that a sequence of generated
numbers should not degenerate, and
the numbers themselves should be evenly[1]
distributed over a given range. Item 3 of Fig. 1 displays
this effect visually.
Our calculation of number p by the Monte-Carlo method (and not in vain a roulette is mentioned) – is a pure perversion (pardon, derivation): the same number p (or an integral) is easily calculated by direct means – see the end of item 5. But nevertheless our perversion was not too much perverted.
Firstly, having solved the task in Fig. 1 we, in principle, have not calculated the value of number p but have verified properties of the pseudorandom number generator, that is quality-factor of the built-in function rnd. At a number of «pebble castings into the water» tending to infinity, an inaccuracy of the Monte-Carlo method should tend to zero provided the function rnd operates correctly.
Secondly, there are figures which areas are impossible to be calculated conventionally, without «perversions». An example is – an area of a cloud snapped from space. The area is rather accurately and, chiefly, quickly (because nobody needs a yesterday's forecast in meteorology) calculated by poking a needle in a random way into the snapshot several times, and … see Fig. 1.
Conventional methods for calculation of a figure area (or an integral) do not suit here not only because cloud contours are impossible to be outlined by any integrable function but also because they are diffused, fuzzy.
A new tendency has appeared in mathematics,
the most precise science in the world: the indistinct set theory (another term
is – «fuzzy sets» but in English it sounds more delicately: «fuzzy sets» –
fluffy sets[2]). The theory
operates with such «pearls» as «it is
rather 1, than 2», «it is rather
plus, than minus», «the point is more
likely to be under the graph than above it» and so on. The basis for this
theory is a well known sophism: «If a
handful of grain is supplemented with a grain whether it becomes a heap? And if
two grains are added? And how many grains will convert the handful into a heap?»
The very how many is a representative
of fuzzy sets the modern number theory and digital computer engineering are
hardly applied to. Programming is properly a jugglery with zeroes and units,
that is the utmost flatness of a human attitude reducing the entire richness of
colors and hues to black and white. Meanwhile the world is composed not of
numbers but of heaps, handfuls, clouds, that is from fuzzy sets modern
computers are not well accommodated to. Those having risen through clouds by
plane know that there is no difference between a cloud and not a cloud. This
will, apparently, carry one of future crises of the programming theory and the
whole computer elemental base. We
shall return to the fuzzy set theory at the end of the etude in the chapter on
distinct and fuzzy logic. For now, let the reader design in the Mathcad
environment a number p calculation technique suggested by Buffon.
Therefore I should repeat once more – our perversion in Fig. 1 was not too much perverted.
We can say that we have drawn in Fig. 1. «a black circle in a black square» imitating Kazimir Malevitch. That is how we have involuntarily intruded into the World of Art …
The art is considered to be based on three foundations. Here they are: sense of proportion, imagination and … need for perversions concerned with doubts and creativity.
Now let’s speak about doubts.
The
volume of a cone, or Pointiller
It can be frequently heard from graduates of aircraft colleges that they never understood the way an iron plane could fly. Many financiers with a higher education do not comprehend (do not accept by soul) clearing settlement operations. Remitting money in an envelope, well, let it be not gold but its substitute (soft money), – is all right yet. And how can money be transmitted by wires (clearing settlements, Internet financial arrangements etc.) – is inconceivable!
The author in his school years very much doubted the triangle angular sum to be equal to 180 degrees. To dispel his doubts he (the author) had drawn almost a thousand triangles, had measured by a protractor and summed their angles! But nevertheless the doubts have remained, since they are justified by the non-Euclidean geometry.
It is very doubtful, that the volume of a cone (and this is the basis of a whole etude of the book – etude 2) equals exactly a third of the volume of a cylinder the cone is inscribed into (see Mathcad manual). Let's check it up.
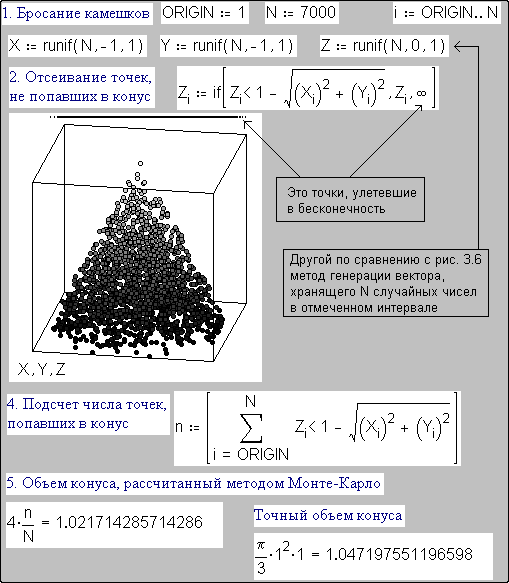
Fig. 2. Calculation of the volume
of a cone
1. Casting pebbles
2. Eliminating points not having hit the cone
The points having flown to infinity
An alternative technique of generation of the vector keeping N random numbers in a specified range
3. Calculation of a number of points having hit the cone
4. The volume of the cone by the Monte-Carlo method
The precise volume of the cone
Fig. 2 presents not only calculation of the cone volume by the Monte-Carlo method but also displays the cone image. Fine arts has a branch called pointilizm (from French pointiller – to paint in points). Its followers paint a picture by individual strokes of regular point or rectangular shape. We have already drawn «a black circle in a black square» in this way. «Still life with a cone» painted in the same style is presented in item 3 of Fig. 2. These is the «fruits» of Scatter Plot labor – a three-dimensional scatter diagram. Thus, insensibly, we have transferred from two-dimensional to three-dimensional graphics – from painting to … sculpture.
The cone was drawn (or more correctly sculptured) in the following manner. «Pebbles» were being cast in a random way at a rectangular parallelepiped of size 2 by 2 by 1 – three vectors X, Y and Z were being generated which elements are random numbers in the range from minus unit to unit (vectors X and Y) and from zero to unit (vector Z, see item 1 in Fig. 2). Points not inscribed into the cone were further eliminated: corresponding elements of vector Z were assigned a value of infinity (item 2), and they… «flew away to the sky» generating a line above the cone (item 2).
Items 3 and 4 – represent calculation of the cone volume by the Monte-Carlo method and its comparison with the true cone volume[3]. The doubts have remained but they are very negligible – within the limits of an error of the Monte-Carlo method.
Sculpture
One great artist had said that sculpture is an easy exercise – just a marble lump is taken and everything superfluous is chopped away. «Any talent is inexplicable. How does a sculptor discern Jupiter concealed in a piece of karrarian marble and brings him out to the world, smashing his shell with a chisel and a hammer?»[4] There is another paradoxical statement: «It is very easy to play the piano. One need push only the right keys in the right time!» All this can be considered to be a kind of bravado or attempts of the Artist to fool his audience bothering him with «foolish» questions on the mystery of creativity. But these ideas are possible to be accepted for a guide to action. We have already examined painting (see Fig. 1) – let’s pitch in sculpture.
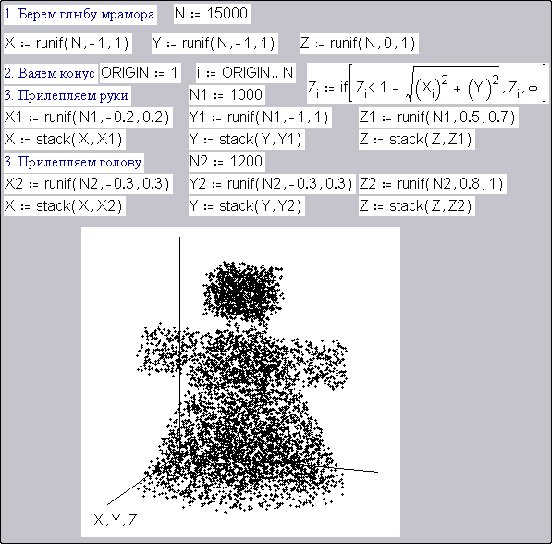
Fig. 2 presents our «marble lump» of size 2 by 2 by 1 and everything superfluous is chopped away (shivers do not fall to the floor, but fly to the sky). For the present we have a standard cone «sculptured», but nothing impedes us to complicate formulas in item 2 of Fig. 2 and to model Venus Milossian or Roden’s Speculator (Thinker)… Fig. 3 illustrates a technique of sculpturing a human figure.
Fig. 3. Computer sculpture
The author had proceeded more easily. He had painted cone points in Fig. 2 green by means of commands of graph formatting and had added some red points of a greater diameter. A quite good New Year's tree had turned out.
At present computers are widely used as painter’s tools (an intellectual brush or something like that). Color printer listings are beautifully framed and exhibited at real and virtual computer-art salons, so to say (see, for example, the magazine «ÊîìïüþÀðò» – CompuArt).
But the author would like to draw attention of respected readers to another problem. This is not simply the problem of computer pictures, but the program listing problem and, in particular, the author would like the reader to pay his attention to the problem of the listing form correspondence (or contraposition) with the program contents.
Programmers with a vivid thinking have noticed a long time ago that procedures and functions have their own «faces», allowing them to be promptly recognized when displayed or printed out. Some procedures are like well-groomed peasant horses, they are plump and sleek and just go on operating, for example, transferring data from one format into another. And they are outwardly unremarkable – they do not attract a rapt attention. Other procedures always aim to spring a surprise, for they are so undebugged (green). And they resemble a runner saddled by a hero of numerous picturesque canvases and sculptures. And there are procedures just crying out to be framed and hung up to the wall for they are so beautiful and perfect, and chiefly, their shape entirely suits their contents. They transmit not only thoughts of their creator painter, pardon, programmer, but also his mood and feelings.
The author is far from being an art critic and does not dare to dilate much on the subject.
Annotations to published computer pictures emphasize, as a rule, authors to be computer artists. Semantic adjectives frequently hide certain defectiveness or, at least, ambiguity of definition: for example, there exists not pure mathematics, but «Applied mathematics». The term computer artist is rather ambivalent. On the one hand, adjective «computer» presents a kind of apologies to a potential spectator for a picture aesthetics (see our figures 1 and 2). And on the other hand, this adjective notifies a spectator of particular tools and methods (avant-garde pretentious novelties) applied at creation of the picture.
The real artist should be prepared to operate with anything and on anything. Pictures of Anatoly Zverev (the artist of a tragic destiny, that, alas, frequently strikes genius people; exhibition of his works has taken place in Moscow in 1999 – see one picture), that were drawn almost with a cigarette stub on paper scraps, are now sold by auction at fantastic sums. Let's wait for printer listings to be exhibited at the Louvre or at the Hermitage or, at the worst, to be sold by art auctions. The latter event will hardly happen. There can be sold a diskette that was owned by a computer artist (but it is a fetish – guitars of grand musicians are now sold like that). The point is that computer art does not distinguish concepts of an original and a copy. And this may kill true masterpieces[5], which are published sometimes on magazine covers or inside glossy editions. Pushkin had been speaking: «That is vulgar – what is popular». Only the most ingenious artworks stand trial of being brought to broad masses. And that is precisely these masterpieces that are of fundamental culture stratum importance for the present-day civilization.
The best way to characterize any phenomena, especially writing an art criticism article, – is to cite a classic quotation. Here it is:
I firstly liked them for specific features
For eyes of blue, for their noble paleness,
For modesty – especially for being freshly charming;
But, God be praised, I’ve found out soon –
It was a sin to know them a little better –
They’re lifeless as if being waxen figures;
But what are ours ones!…
Guess what Pushkin’s Don Juan (Don Guan?) was speaking of! Quite so – he was also speaking of computer animation, of pictures created by means of computer graphics… Let's put it mildly (with a certain hope) – he was speaking about modern samples of this symbiosis of science, process engineering and art. You see, computer pictures make you feel more an imperfect tool (fresh charm – is a paradox of high technologies), than an artist himself.