Решатели
или
Великолепная семерка Mathcad
Богомолова Е.П., Очков В.Ф.
Национальный исследовательский университет «Московский энергетический институт»
Подробная контактная информация об авторах:
Богомолова Елена Петровна, к.ф.-м.н., доцент
Национальный исследовательский университет «Московский энергетический институт»
Адрес: 111250,
Россия, Москва, Красноказарменная ул., д. 14, раб. тел. +7-495-362-73-92,
bogomolovaep@mpei.ru
Очков Валерий Федорович, д.т.н., профессор
Национальный исследовательский университет «Московский энергетический институт»
Адрес: 111250,
Россия, Москва, Красноказарменная ул., д. 14, раб. тел. +7-495-362-71-71,
ochkov@twt.mpei.ac.ru, skypeOchkovVF
Аннотация
В статье рассмотрены основные математические инструменты Mathcad, позволяющие решать уравнения и их системы аналитическими, численными и графическими методами
Ключевые слова: Mathcad, уравнение, система уравнений, алгебраическое уравнение, дифференциальное уравнение
Solvers
or
The Magnificent Seven of Mathcad
Bogomolova E.P., Ochkov V.F.
National research university «MPEI»
Abstract
The article describes the basic
mathematical tools of Mathcad that allow solving equations and systems of
equations by analytical, numerical and graphical methods.
Keywords:
Mathcad, an equation,
system of equations, algebraic equations, differential equation
Многие задачи по математике,
физике, химии и другим школьным и вузовским дисциплинам сводятся к решению
уравнений и систем уравнений. Поэтому полезно будет узнать, какие инструменты
для решения такого рода задач есть у пакета Mathcad, очень популярного у школьников,
студентов инженеров и ученых. Эти инструменты объединены в группу «Решение уравнений» встроенных функций Mathcad, которые используют различные численные методы. В среде Mathcad 15 названия этих методов можно
узнать, если на имени некоторых функции, их реализующих, нажать правую кнопку
мыши. В группе «Решение
уравнений» традиционно
находятся семь функций (см. второе
название статьи). Есть еще в среде Mathcad и оператор solve для
символьного (аналитического) решения задач. Описание этих инструментов будет
сделано на несложных школьных "водных" примерах.
Задача 1. Моторная лодка прошла по реке в
одну сторону (L = 10 km), а потом вернулась в исходную
точку, затратив на этот «круиз» 1 час 45 минут (t).
Спрашивается, какова скорость течения воды в реке (неизвестная х),
если собственная скорость лодки (v–скорость в стоячей воде) равна
12 км/ч (kph).
Раньше подобные «школьные»
задачи решались в несколько действий. Но не всякая задача может быть решена по
действиям. Поэтому люди и придумали алгебру[1]. (Эту
задачу тоже сходу нельзя решить пошагово[2]).
Сейчас принято составлять, а затем решать уравнения,
выбирая их подходящие корни. Пойдем и мы по этому пути, но, составив уравнение,
попробуем решить его не на бумаге, а на компьютере в среде математической
программы Mathcad. В нашей задаче о моторной лодке время в пути t
– это суммарное время, затраченное на поездку в одну сторону L / (v + x) (условно будем считать, что это движение по течению реки), и в обратную сторону (против
течения) L/ (v – x). Поэтому наше уравнение будет иметь вид:
(L / (v + x)) +(L / (v – x)) = t.
0. solve
Начнем с решения
полученного уравнения средствами символьной
математики Mathcad.
Формальное, более длинное название символьной математики – компьютерные аналитические преобразования, но у нас прижилась
калька с английского – symbolic
math. Это название мы и будем
использовать далее.
Если численная математика (которая,
повторяем, тоже есть в среде Mathcad
и составляет его основу) оперирует числами, хранящимися в переменных, то символьная математика работает с самими
переменными-символами.
На рисунке 1 показано
решение уравнения движения моторной лодки по реке с помощью команды solve символьной
математики Mathcad
(на этом и некоторых других рисунках будут показаны позиции меню и панели
инструментов Mathcad Prime
и Mathcad
15 для решения описываемых задач).

Рис. 1.Аналитическое решение
задачи о движении моторной лодки
Из
полученного общего аналитического решения (из вектора с двумя
элементами-формулами – см. рис. 1) можно скопировать один элемент, подставить в
него исходные значения переменных L, t и v (см. рис. 2) и получить
численный ответ – скорость течения воды в реке. Ответ будет выдан в метрах,
деленных на секунду (Mathcad
по умолчанию ориентирован на СИ), и подправлен на более привычные километры в
час (kph). Mathcad – это не просто математический,
а физико-математический пакет [1]: переменные Mathcad хранят не просто числа, а
физические величины (длину, время, силу, массу и т.д.), что очень полезно при
расчетах задач с физическим смыслом. Это существенно ускоряет и упрощает расчеты,
позволяет избежать ошибок в них.
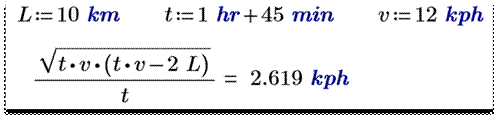
Рис. 2.Решение задачи о моторной
лодке по найденной на рис. 1 формуле
Спрашивается, для
чего же тогда в пакете Mathcad
есть и численная математика, если задачу можно просто и красиво решить с
помощью символьной математики? Дело в том, что символьная математика,
нацеленная на выдачу всех решений в виде формул (абсолютная точность!), часто
не справляется с более-менее сложной задачей, и это показано на рис. 3 и 4.

Рис. 3. Поиск корня уравнения:
очень объемный ответ
На рисунке 3 в
уравнении движения моторной лодки один из иксов был возведен в квадрат.
Физический смысл уравнения пропал[3]
(складывается скорость с квадратом скорости[4]).
Но сейчас не это главное. Важно то, что пакет Mathcad, решив это чуть усложненное
уравнение, не смог вывести на дисплей ответ – настолько тот оказался
громоздким. Но это еще полбеды. Настоящая «беда» показана на рис. 4 для еще
более усложненного уравнения. Если, например, один икс возвести в квадрат, а
другой в куб (рис. 4), то символьная математика Mathcad «поднимет руки вверх и скажет:
«Сдаюсь!».

Рис. 4. Поиск корня уравнения:
решение не найдено
Если в константы
этого «нефизического» уравнения подставить безразмерные численные значения
известных величин, то хотя бы один действительный корень у этого уравнения
найти удастся – см. рис. 5, где данная задача решена графически.
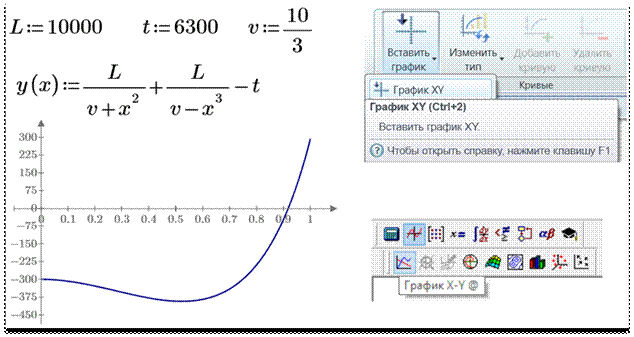
Рис. 5. Графический поиск нуля
функции
1. root+root
Из рисунка 5 видно,
что у нашего уравнения, превращенного в функцию пользователя переносом
переменной t
в левую часть, есть как минимум один действительный корень в районе числа 0.9.
Уточнить численное значение этого корня поможет встроенная в Mathcad функция root
– см. рис. 6 и 7.
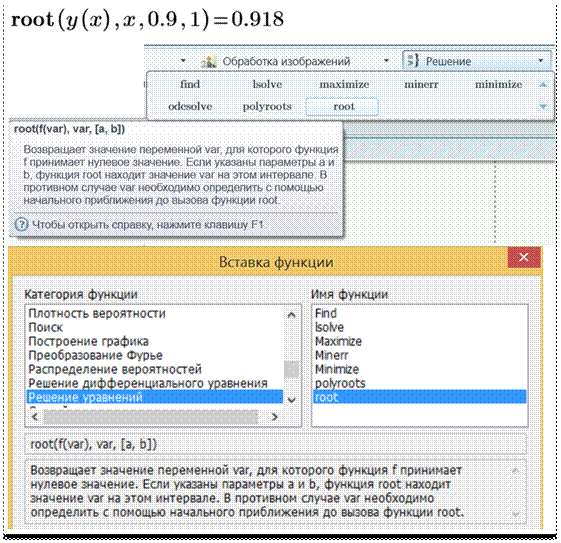
Рис. 6. Работа в среде Mathcad встроенной функции rootс четырьмя аргументами
На рисунке 6 показан
вызов функции root
с четырьмя
аргументами, а на рис. 7 с двумя. В обоих случаях ответ выведен с точностью в
три знака после десятичной точки. Но можно вывести и большее число знаков – до
15. В первом случае нуль функции y(х)
ищется методом
деления пополам на интервале, заданном третьим и четвертым аргументами функции root
(см. авторскую анимацию этого метода на сайте
http://communities.ptc.com/videos/1468). Во втором случае (рис. 7) нуль функции
рассчитывается методом секущих с опорой на первое приближение х := 1 (http://communities.ptc.com/videos/1466). В среде Mathcad для вычисления нуля функции
пользователя фактически есть две одинаковые по имени, но разные по своей сути
встроенные функции root.
![]()
Рис. 7. Работа в среде Mathcad встроенной функции root
с двумя аргументами
На рисунке 8 показана
работа функции root
на довольно простом примере – с функцией пользователя sin(x)/x,
которая имеет бесконечное число нулей. На отрезке [2,7] функция y(x)
имеет два нуля (π и 2π), но четырехаргументная
функция root ответ
не дала, так как функция y(x) имеет одинаковые знаки на концах
этого отрезка и функция root считает, что там не может быть
корней уравнения. На отрезке [1,17] нулей уже пять, один из которых (9.425)
найден четырехаргументной функцией root. На концах отрезка [1,17] функция y(x)
уже имеет разные знаки. При первом приближении, равном 0.01, двухаргументная функция root выдала не ближайший
нуль (3.14), а «очень-очень дальний»: 298.451. Понять эти особенности
применения функции root можно только после детального
изучения численных методов, заложенных в эту функцию.
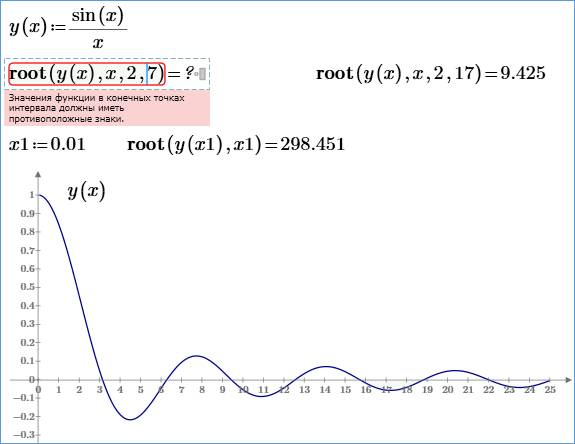
Рис. 8. Особенности работы
функции root
Ранее мы отметили,
что символьная математика Mathcad
оперирует не числами, а символами – самими переменными, хранящими или не
хранящими числа. Но это не совсем так.
Если какая-либо
переменная выражения хранит численное значение, то символьная математика будет
работать не с самой переменной (с символом), а с числом, хранящимся в этой
переменной. На рисунке 3 была показана осечка символьной математики Mathcad при решении довольно простого
уравнения. Но если всем переменным этого уравнения, кроме переменной x,
задать численные
значения, то символьный оператор solve
успешно
справится с задачей – см. рис. 9.

Рис. 9. Численный ответ
символьного оператора
На рисунке 9
показано, что «символьный» оператор solve в отличие от «численной» функции root выдал все четыре корни уравнения
(один действительный и три комплексных) без установки интервала или первого
приближения. Кроме того, если численная математика при выводе ответа «на
печать» по умолчанию, как мы уже отметили, ограничивается тремя знаками после десятичной
точки, то символьный оператор solve в этом случае выдал численные
решения с двадцатью знаками после запятой. При «численном» ответе количество
значащих цифр можно увеличить до 15, а при символьном до 250.
Примечание. Лишить переменную ее численного
значения для последующих аналитических преобразования можно операторами: сlearsym(a) (Mathcad Prime) и a := a (Mathcad 15).
Если наше уравнение с
численными константами (см. рис. 9) и дальше усложнять, то на каком-то этапе
оператор solve
не сможет найти
корни. Функция же root
по-прежнему
будет выдавать корень, правда, лишь один из многих и с опорой на заданный интервал
поиска (рис. 6) или на первое приближение (рис. 7). При этом задавать интервал
поиска придется, исходя из уверенности, что корень на этом интервале имеется. Метод
секущих же при неправильном первом приближении вообще не выдаст нужного
результата. Это такой своеобразный компромисс. Отсюда общее правило:
поставленную математическую задачу нужно стараться сначала решить аналитически
в общем виде, не придавая переменным конкретных численных значений (рис.1) или
придавая отдельным или всем переменным численные значения (рис. 9). Если же это
не получается, то придется переходить к поиску частных решений численными
методами.
На рисунке 10
показано использование графика и функции root в двух ее вариантах для решения нашей задачи о
моторной лодке. Интересный факт. Двухаргументная
функция root
при первом
приближении, равном нулю, выдала не ожидаемый положительный, а отрицательный
корень. Этот нюанс можно понять, если опять же учесть особенности метода
секущих при поиске нулей функции и после построения графика не на отрезке от -3
до 3 kph,
а на отрезке -13 до 13 kph, охватывающем точки разрыва, что
мы сделаем ниже.
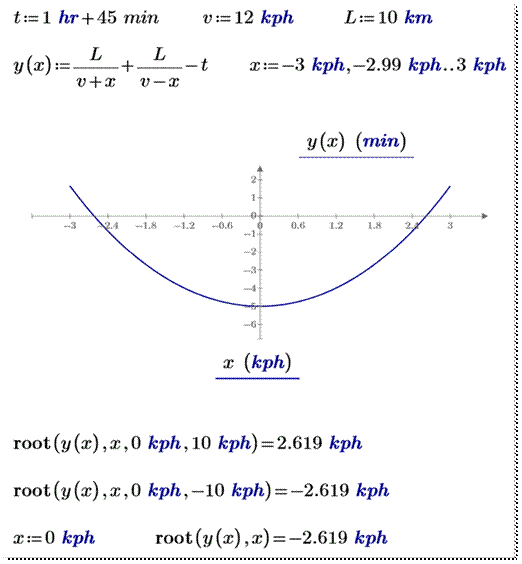
Рис. 10. Графическое и численное
(функция root) решение задачи о моторной лодке
Уравнение движения
моторной лодки, показанное на рис. 1, можно преобразовать в квадратное. К
такому приему часто прибегают в школах, т.к. школьников, как правило, учат
аналитически решать только квадратные уравнения. Как такое преобразование можно
сделать в среде Mathcad,
показано на рис. 11.

Рис. 11. Определение
коэффициентов полинома
Оператор символьной
математики simplify
(упростить) приводит
левую часть исходного выражения к общему знаменателю, умножает обе части
уравнения на полученный знаменатель и переносит все слагаемые в левую часть
уравнения (рис. 11). Таким способом выделяется функция, которая приравнена к
нулю. Оператор coeffs
находит
коэффициенты этой функции-полинома (в данном случае квадратного). Это
квадратное уравнение можно решить оператором solve, но… см. ниже.
Примечание. Квадратичная функция,
полученная после преобразования исходного уравнения движения моторной лодки, не
эквивалентна исходной функции, а только имеет с ней два одинаковых корня. В
этом можно убедиться, взглянув на графики, показанные на рис. 12. Наше исходное
уравнение движения моторной лодки имеет разрывы при x, равном
12 и минус 12 kph. В этих точках лодка не
перемещается относительно берега. Квадратичная же функция таких разрывов,
естественно не имеет
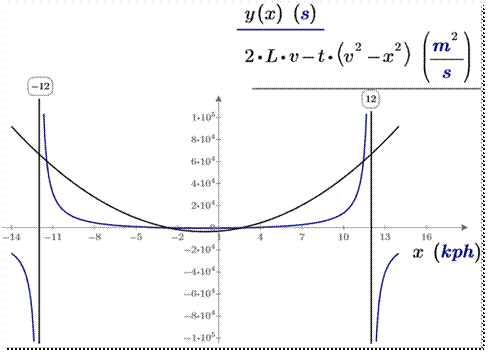
Рис. 12. Исходное и квадратное
уравнение движения моторной лодки
2. polyroots
Если выражение
представляет собой полином (квадратный, например, см. выше), то можно найти все
его нули, использовав еще одну функцию из «великолепной семерки Mathcad» – функцию polyroots.
Она имеет в качестве аргумента вектор коэффициентов полинома и возвращает его
нули (вектор, который на один элемент короче вектора-аргумента – см. рис. 13),
т.е. решение нашей задачи.
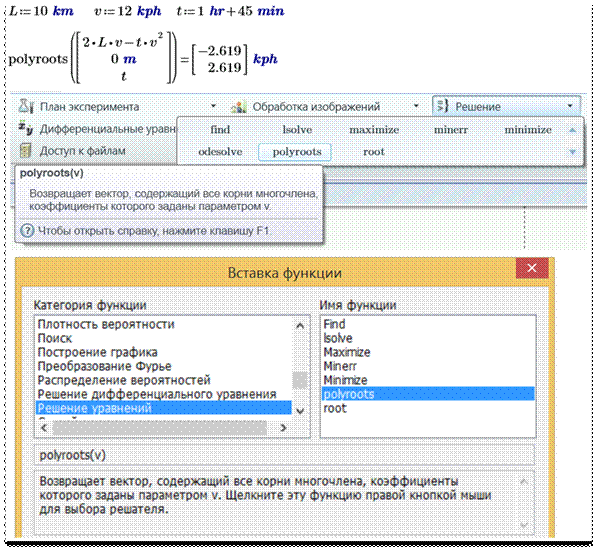
Рис. 13. Поиск нулей полинома в
среде Mathcad
В
нашей задаче о движении моторной лодки полином оказался квадратным и его корни,
повторяем, можно было найти через оператор символьной математики solve (см. рис. 1). Но в случае
полиномов высокой степени оператор solve
не сработает. Тут
и пригодится численная встроенная функция polyroots.
3. Find
Показать работу еще
одной функции из «великолепной семерки Mathcad» – функции Find – поможет нам еще одна
дополнительная моторная лодка.
Задача 2. От двух пристаней на
прямолинейном участке реки навстречу друг другу[5]
одновременно отходят две моторные лодки. Они встречаются в точке, делящей этот
участок реки в золотом соотношении[6].
Найти скорость второй лодки v2
и скорость
течения воды в реке v, если известна скорость первой
лодки v1, расстояние между пристанями L
и время t
движения лодок
до встречи.
Золотое соотношение
(сечение) в задачу вставлено неслучайно. Можно поискать в своей памяти или в
справочниках (бумажных или интернетовских) формулу золотого сечения. Но можно поступить иначе [2]: в среде Mathcad написать само уравнение золотого
сечения применительно к нашей задаче о моторных лодках и решить его
аналитически, получив нужную формулу – см. рис. 14.
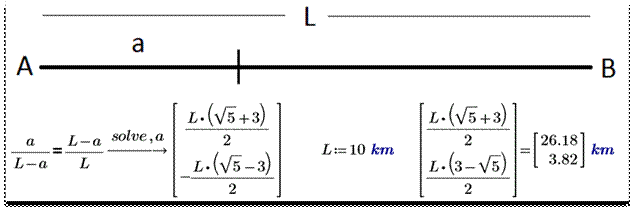
Рис. 14. Решение уравнения
золотого сечения в среде Mathcad
На рисунке 14
оператор solve
выдал два
решения, из которых нам подходит только второе – 3.82 km. Первое же решение (26.18 km) лежит вне рассматриваемого
отрезка. Символьная математика, повторяем, выдает все ответы, из которых нужно
еще уметь выбрать подходящее. Или уметь заставить оператор solve выдать нужный ответ.
На рисунке 15
показано решение в среде MathcadPrime и Mathcad 15 задачи о двух моторных
лодках, сводящееся к решению системы двух уравнений с двумя неизвестными.
Решение найдено с помощью функции Find, требующей начального приближения
к решению.

Рис. 15. Решение систем
алгебраических уравнений с помощью функции Find
Встроенная функция Find меняет
значение своих аргументов, начиная от начального приближения так, чтобы
уравнения системы превратились в тождества. Вернее, почти в тождества. Дело в
том, что и обе функции root
(рис. 7 и 9) и
функция Find
(рис. 7) возвращают значения, отличающиеся от точных решений на величину, не
превышающую по модулю значения, хранящегося в системной переменной CTOL.
Ведь что такое корень уравнения?! Корень – это значение переменной, при котором
уравнение превращается в тождество. Но при численном (приближенном!) решении
найти точный корень не всегда удается. Подстановка приближенного значения корня
в уравнение приводит к тому, что правые и левые части уравнения отличаются друг
от друга на значение, хранимое в переменной CTOL, которое по умолчанию равно
0.001. Это значение можно менять, решая конкретную задачу. На сайте с авторской
анимацией http://communities.ptc.com/videos/1472 можно видеть особенности
поиска четырех корней системы двух нелинейных уравнений: уравнения эллипса и
уравнения лемнискаты Бернулли. На сайте http://communities.ptc.com/videos/2418
можно увидеть анимацию, как выбор первого приближения влияет на найденный
корень. Более подробно о методах решения, заложенных в функцию Find,
можно почитать в работе [3]. На сайте http://communities.ptc.com/videos/1472
помещена авторская анимация последовательного численного поиска корней двух
нелинейных у равнений методом Ньютона.
Примечание.
Переменная L,
которой на рис. 15 присваивается значение 10 km (L :=
10 km), подчеркнута волнистой чертой,
указывающей на ненормальную расчетную ситуацию (Mathcad
15). Переменная L по умолчанию хранит значение
одного литра (единица вместимости) и это значение переопределяется. В среде Mathcad Prime эта недоработка исправлена – там
есть две независимые переменные L: литр и отдельная
пользовательская переменная, хранящая расстояние.
4. lsolve
Можно понять, что
система двух алгебраических уравнений движения двух моторных лодок навстречу
друг другу, показанная на рис. 15, линейна,
и применить к ней еще одну функцию из «великолепной семерки Mathcad» – функцию lsolve,
предназначенную для решения (solve)
именно систем линейных (l)
алгебраических уравнений (СЛАУ) – см. рис. 16.
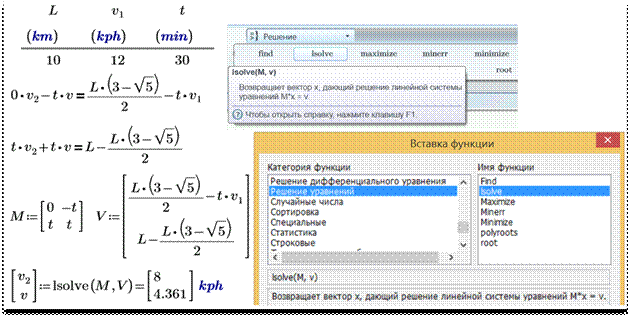
Рис. 16. Решение СЛАУ в среде Mathcad
На
рисунке 16 система уравнений (показанная на рис. 15), преобразована к виду
классической линейной системы: слева неизвестные v2 и v со
своими коэффициентами, справа – свободные члены. Функция lsolve имеет два аргумента: матрицу
коэффициентов при неизвестных СЛАУ (у нас это M) и
вектор свободных членов V. Возвращает функция lsolve вектор найденных значений
неизвестных. При решении СЛАУ с помощью функции lsolve (рис. 16) начальные приближения
(см. рис. 15) вводить не надо, т.к. у этой системы либо есть, причем
единственное решение, либо решений совсем нет, либо решений бесконечно много. В
[2] дан графический анализ этой особенности с привлечением понятия ранга
матрицы.
5 и 6. Minimize&Maximize
Об очередной функции
«великолепной семерки» ─ о функции Minimize,
будет рассказано на примере задачи
оптимизации, связанной также с «водным транспортом».
Задача 3. Определить крейсерскую скорость
судна – скорость при которой затраты на его эксплуатацию будут минимальны.
Задача предельно
упрощена – затраты на эксплуатацию судна состоят из двух частей: почасовой
зарплаты экипажа, пропорциональной времени движения судна (обратно
пропорциональной скорости судна), и затрат на горючее, пропорциональных
квадрату скорости судна (коэффициенты пропорциональности – а
и b).
Увеличивая скорость судна, мы экономим на зарплате экипажу, но при этом
приходится больше тратить денег на горючее. Попробуем найти тут оптимальное
решение!
На рисунке 17
показано решение этой типичной задачи оптимизации с помощью встроенной функции Minimize
с графической иллюстрацией решения.
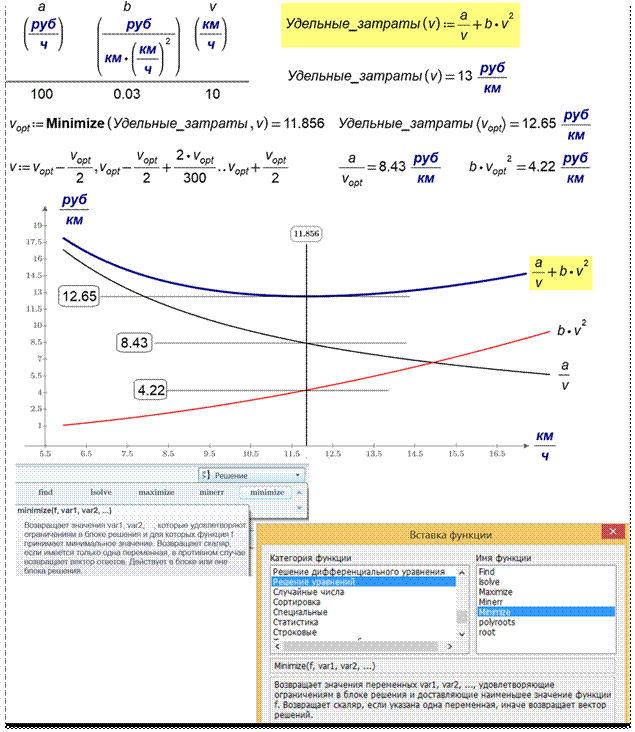
Рис. 17. Нахождение крейсерской
скорости судна численной математикойMathcad
Функция Minimize меняет значение своего второго
аргумента, начиная от заданного предполагаемого значения (у нас это 10 км/ч)
так, чтобы значение первого аргумента (целевой функции Удельные_затраты) приняло минимальное значение. Если бы мы не
минимизировали затраты, а максимизировали, например, прибыль владельца судна,
то нужно было бы при решении такой задачи функцию Minimize заменить на функцию Maximize.
В оптимизационных задачах часто присутствуют ограничения – скорость судна,
например, не может превышать максимально допустимую. В этом случае функции Minimizeили Maximize нужно будет поместить в область Ограничения блока Решить, показанного
на рис. 15.
Найти минимум нашей
целевой функции Удельные_затраты
можно и
средствами символьной математики Mathcad, что показано на рис. 18.

Рис. 18. Нахождение крейсерской
скорости судна символьной математикойMathcad
На рисунке 18 ведется
поиск нулей первой производной функции по удельным затратам на километр пути
судна. Но если затраты на топливо будут зависеть от скорости судна, взятой не
во второй степени, а в степени n, то символьная математика уже не
справится с такой усложненной задачей (рис. 19), и придется вернуться к
численным методам решения задач (рис. 17).

Рис. 19. Осечка при работе с
символьной математикой Mathcad
7. Minerr
Последняя функция
«великолепной семерки» Mathcad
– это функция Minerr
(Minimal Error – минимальная ошибка). Если
функция Find
(см. рис. 15) не
находит решения системы уравнений, то она возвращает сообщение об ошибке.
Функция же Minerr
в такой ситуации
возвратит не сообщение об ошибке, а значения своих аргументов (невязку
системы), при которых система уравнений будет максимально приближена к системе
тождеств – точку последнего приближения к решению. В старых версиях Mathcad не было функций Minimize и Maximize,
и задачи оптимизации приходилось решать именно через функцию Minerr.
На рисунке 20
показано, как эта функция решает задачу определения крейсерской скорости судна:
при оптимальном движении затраты на эксплуатацию судна будут максимально
приближены к нулю рублей на километр пути.
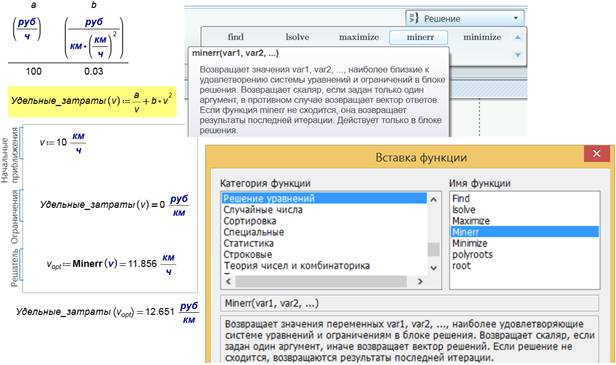
Рис. 20. Решение задачи
оптимизации с помощью функции Minerr
Функцию Minerr можно считать главной
в «великолепной семерке[7]Mathcad», т.к. ею можно заменить и
функцию Find, и функцию root (в двух ее вариантах), и функцию polyroots,
и функцию lsolve, и в ряде случаев функции Minimize и Maximize.При
использовании функции Minerr надо обязательно предусматривать
проверку решений. Нередки случаи, когда решения могут оказаться ошибочными,
чаще всего из-за того, что из нескольких корней находится нереальный (или не
представляющий интереса) корень. Дело в том, что функция Minerr пытается
найти максимальное приближение к искомому числу путем минимизации
среднеквадратической погрешности решения. Следует заранее убедиться в том, что
решение существует, и как можно точнее указать начальное приближение к решению.
Компьютерная
математика с универсальными и скрытыми от пользователей методами аналитических
и численных решений заставляет нас забывать о типах уравнений. Вспомним о них!
Типы уравнений
Для того чтобы без проблем и правильно решать уравнения и
системы уравнений, нужно знать не только специфику численных методов (см.
выше), но и свойства самих уравнений. Математики уравнения с одним неизвестным
относят к одному из четырех типов: алгебраические, рациональные, иррациональные
и трансцендентные. Метод аналитического решения определяется типом решаемого
уравнения.
Если полином n-й степени приравнять нулю, то мы получим алгебраическое
уравнение. Основная теорема алгебры говорит о том, что такое уравнение имеет
ровно n корней. Но во-первых, не все корни будут действительными и,
возможно, вообще не существует ни одного действительного корня. А во-вторых,
корни могут совпадать, т.е. быть кратными. Доказано, что не существует формул
для корней алгебраического уравнения выше пятой степени. Но и формулы для n = 5 настолько громоздки, что их
использование лишено какой-либо практической пользы. Mathcad может решать
алгебраические уравнения вплоть до четвертой степени (даже символьно).
Если уравнение более высокой степени допускает частичное
разложение на множители, то оно тоже может быть символьно разрешимо. Тут
уместно вспомнить школьный метод подбора целого корня и теорему Безу. Если
алгебраическое уравнение имеет целые коэффициенты, и делители свободного члена
известны, то можно подобрать целый корень х0 (если такой имеется)
«вручную», либо использовав Mathcad. Поделив полиномиальную функцию на двучлен
(х
- х0), получим алгебраическое уравнение степени
на единицу меньше. Если целый корень не подбирается, то такое уравнение теряет
свои преимущества и становится в один ряд с другими типами уравнений.
Рассмотрим теперь рациональные уравнения. Такие уравнения
содержат исключительно дроби, в числителях и в знаменателях которых находятся
только многочлены. С помощью Mathcad эти уравнения легко формально
преобразовать в алгебраические. Правда, при таких преобразованиях может
измениться область допустимых значений преобразуемого уравнения, т.к.
знаменатель какой-то дроби может оказаться в числителе. Это порождает проблему
посторонних корней, а поэтому решение рационального уравнения требует
обязательной проверки (подстановки полученных чисел в исходное уравнение). Если
все дроби в рациональном уравнении «одноэтажные», то проверку можно заменить
предварительным поиском области определения рациональной функции, приравняв
нулю все знаменатели. Если дроби «многоэтажные», то такая процедура потребует
априорных упрощений. Если хоть в одном из знаменателей находится многочлен
третьей или более высокой степени, то поиск допустимых значений оборачивается
поиском корней нового алгебраического уравнения. В таком случае проверка –
более экономный способ отсечения посторонних корней.
Иррациональными
называют такие уравнения, которые помимо рациональных функций содержат радикалы
(корни целых степеней – квадратные, кубические и т.п.), а все подкоренные
выражения являются рациональными функциями. Известно, что радикалы четных
степеней определены не везде в действительной области. Это обстоятельство
приводит к необходимости находить область определения прежде, чем решать само
уравнение. Фактически само уравнение следует сопроводить неравенствами, которые
Mathcad тоже будет решать. Если этого не слелать, то уравнение по умолчанию будет решаться на
области комплексных чисел, которые для большинства пользователей, исследующих
реальные физические и другие явления, попросту бесполезны.
Вторая
проблема, возникающая при решении уравнений с радикалами четных степеней –
появление посторонних корней. Ведь основным методом решения иррационального
уравнения является метод возведения обеих частей уравнения в нужную степень, а
при возведении в четную степень как числа х, так и числа –х, мы получим один и тот
же результат. В итоге получается новое уравнение, строго говоря, не
равносильное исходному. Заметим, что есть аналитические способы решения и
уравнений с кубическими (и другими нечетными) радикалами, которые тоже приводят
к посторонним корням. Но тут снова
можно прибегнуть к проверке, т.е. подстановке полученных числовых величин в
исходное уравнение. Следует помнить, что лишние корни вполне могут принадлежать
области определения функции, приравниваемой нулю.
Класс
трансцендентных уравнений обширен. В него входят показательные,
логарифмические, тригонометрические уравнения, а также уравнения, содержащие
различные (а не только степенные)
элементарные функции и композиции элементарных функций. Помимо проблем,
связанных с областью определения, в таких уравнениях при наличии тригонометрических функций могут
возникнуть проблемы с периодичностью решений.
В
зависимости от того, сколько неизвестных входят в систему уравнений, можно
выделить два типа систем: системы с одним неизвестным и системы с несколькими
неизвестными. Классификация всех систем – занятие бессмысленное, поскольку
специальные эффективные (матричные) методы решения разработаны только для
систем линейных алгебраических уравнений с несколькими неизвестными. Такие
системы еще называют линейными алгебраическими системами. Все другие системы
решаются с помощью одних и тех же общих численных методов.
Системы с
одним неизвестным можно решить так: найти по отдельности решение каждого
уравнения системы, а потом выбрать одинаковые для всех уравнений числа. Часто
можно поступить проще: сначала решить то уравнение, которое имеет наименьшее
число корней, а потом все эти корни подставить в каждое из оставшихся уравнений
системы.
Нелинейные
системы с несколькими неизвестными решаются численными итерационными методами,
требующими задания начального приближенного значения искомых неизвестных.
Выбор метода
Посмотрим, чем же стоит руководствоваться при
выборе метода решения конкретного уравнения или системы.
Для
вычисления всех корней алгебраического уравнения не выше пятой степени
рекомендуется использовать символьные вычисления а также функцию polyroots, поскольку она не требует проведения процедуры локализации
корней. Во всех остальных случаях придется либо локализовать корень на
конкретном отрезке, либо использовать итерационные методы, имея достаточно
хорошее начальное приближение и выбрав подходящую точность вычислений.
Прежде чем
начать поиск корней уравнения, нужно на нескольких различных интервалах
построить график функции, приравниваемой к нулю. Поведение графика даст ответ
на несколько вопросов. Имеет ли функция действительный корень? Где он расположен?
Сколько всего действительных корней? Отделены ли корни друг от друга, или они
имеют некоторую точку скопления? Можно ли считать, что корни периодически
повторяются, и чему равен период? Есть ли у функции точки разрыва, и насколько
далеко от них лежат корни? Следует ли уменьшить значение системной переменной CTOL, чтобы различить два близко
расположеных корня?
Когда
ответы на все вопросы получены, тогда можно определиться с методом и точностью
вычислений.
Заметим,
что если проигнорировать этап построения графика функции, то, например, функция
root может сработать некорректно. Правда,
по графику нельзя определить, попадет ли в процессе решения в точку локального
минимума невязки последовательность приближений. Если причина ошибки в этом, то
нужно задать другое начальное приближение.
Чем точнее выбрано начальное приближение корня, тем быстрее итерационный
процесс будет сходиться.
Результатом решения системы будет численное
или символьное значение вектора неизвестных величин. При символьном решении не надо
вводить начальные значения, а при численном – надо. Если в системе всего два
неизвестных, то построение трехмерных графиков функций, входящих в систему,
позволит удачно подобрать начальное приближение для решения системы. В случае
неудачного начального приближения появится сообщение об отсутствии сходимости
последовательности итераций. Тогда придется начать все сначала, задав другое
первое приближение.
Широкое
использование компьютеров для поиска корней уравнений привело к тому, что
многие пользователи перестали чувствовать разницу между алгебраическими,
рациональными, иррациональными и трансцендентными уравнениями. Более того, все
эти уравнения стали называться просто алгебраическими. Так в документации Mathcad сказано,
что этот пакет может численно решать и системы алгебро-диффренциальных
уравнений – системы, где присутствуют и алгебраические и дифференциальные (см.
ниже) уравнения. Хотя там могут быть и другие типы уравнений – рациональные,
иррациональные и трансцендентные.
В Mathcad Prime к великолепной семерке добавилась еще
одна функция – функция Odesolve.
7+1. Odesolve
Наша первая задача о «круизе» моторной лодки туда (см. рис. 1
и 2) имела существенное допущение: скорость лодки была постоянной. Но это
условие выполнить практически невозможно, т.к. лодка по прибытии в один конец
пути должна сбросить скорость, развернуться и пуститься в обратный путь. Можно,
конечно, переформулировать задачу так: лодка достигает конечной точки и в этот
момент эстафету принимает другая моторная лодка, движущаяся с такой же собственной
скоростью, но в обратном направлении. Приблизить задачу об одной лодке к
реальным условиям нам поможет еще одна встроенная функция Mathcad – функция Odesolve, предназначенная для решения (solve)
обыкновенных (o - ordinary) дифференциальных (d) уравнений (e – equation) и их систем. Если при численном решении алгебраических
уравнений мы получаем числа, подстановка которых в уравнения превращает их в
тождества, то при решении дифференциальных уравнений и их систем мы получаем уже
не числа, а функции, подстановка
которых превращает исходные дифференциальные уравнения в тождества. Заметим,
что функция Odesolve
в группе «Решение уравнений» стала восьмой (7 + 1 – см.
выше) только в среде MathcadPrime. В Mathcad 15 в
группе «Решение уравнений» ее не было.
Итак, задача 4. На
моторной лодке, движущейся со скоростью v,
заглушили мотор. Спрашивается, как будут меняться во времени пройденный ею
путь? Задача предельно упрощена – на лодку действует силы трения воды и воздуха,
пропорциональные квадрату скорости лодки (см. рис. 17, 18, 19 и 20, где этот
квадрат фигурировал). На рисунке 21 показано решение с помощью функции Odesolve
и графическое отображение решения.
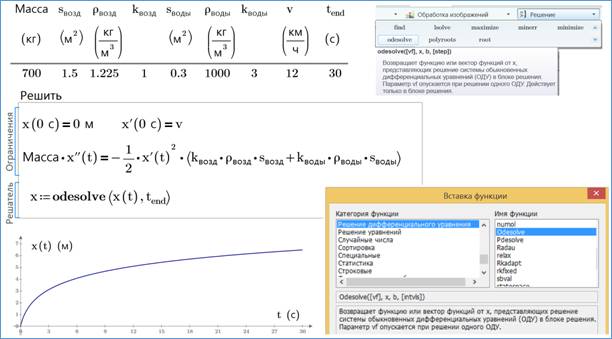
Рис. 21. Решение задачи об
остановки лодки
Коэффициент
пропорциональности между инерцией и силой трения, записанный в уравнении на
рис. 21 (масса лодки, помноженная на ускорение – на первую производную скорости
по времени), состоит из двух частей, связанных с трением о воздух надводной
части лодки и трением о воду ее подводной части. Эти коэффициенты
пропорциональны плотности ρ среды (воздуха или воды) и
площади поперечного сечения надводной и подводной частей лодки S. В уравнение можно добавить силу
тяги мотора и моделировать также старт моторной лодки и ее последующее движение
с переменной и постоянной скоростью. Если скорость лодки станет постоянной, то
дифференциальное уравнение превратится в алгебраическое: сила тяги мотора будет
уравновешиваться силой сопротивления воды и воздуха.
Задачу
об остановке моторной лодки мы решили численно: функция Odesolve не ищет аналитического решения
уравнения. Она формирует таблицу значений искомой функций x (пройденный
путь), по которой методом интерполяции создается непрерывная функция, график
которой мы построили (см. рис. 21). На сайте http://communities.ptc.com/videos/1471
можно просмотреть авторскую анимацию численного решения обыкновенного
дифференциального уравнения методами Эйлера и Рунге-Кутта.
В
среде Mathcad
нет средств аналитического (символьного) решения дифференциальных уравнений. Но
их можно поискать и найти в Интернете. На рисунке 22 показано такое решение –
логарифмическая функция. Оно нашлось, поскольку исходное уравнение было
достаточно простым: вторая производная функции пропорциональна квадрату ее
первой производной. Но если с нашей
задачи о движении лодки начать снимать ограничения, то символьного решения уже
не будет, и нам придется возвращаться к численным методам – к функции Odesolve.
Так, например, при торможении лодки площадь поперечного сечения ее надводной
части уменьшается (лодка проседает в воду), а подводной части растет[8]. Коэффициенты
kвозд и kводы (см. блок исходных данных на рис. 21) также зависят
от скорости и характера движения лодки: они одни при ламинарном («гладком»)
обтекании тела и другие при турбулентном движении, когда за лодкой клубятся
вихри воды и воздуха. У воды и воздуха разная вязкость, что тоже нужно
учитывать при математическом моделировании движении лодки. Этим занимается
очень интересная наука под названием гидрогазодинамика…
И последнее. После
нахождения корня алгебраического уравнения (или решения системы) всегда,
независимо от метода, стоит сделать проверку
– подставить найденное значение (найденные значения) в уравнение (в систему) и
убедиться, что получилось тождество. Или почти тождество, если используются
численные (приближенные) методы решения. Проверка решения рассматриваемого
дифференциального уравнения может заключаться в построении графика баланса сил
и произведения массы на ускорение (если иметь ввиду задачу, показанную на рис.
21) в зависимости от аргумента полученной функции (t – см. рис. 21). Этот график
должен совпадать с осью x.
Кроме того, если есть аналитическое решение дифференциального уравнения, то его
можно сравнить с численным решением. Мы это сделали в расчетном документе,
показанном на рис. 22, где Mathcad-документ
(численное решение задачи об остановке лодки) дополнен аналитическим решением.
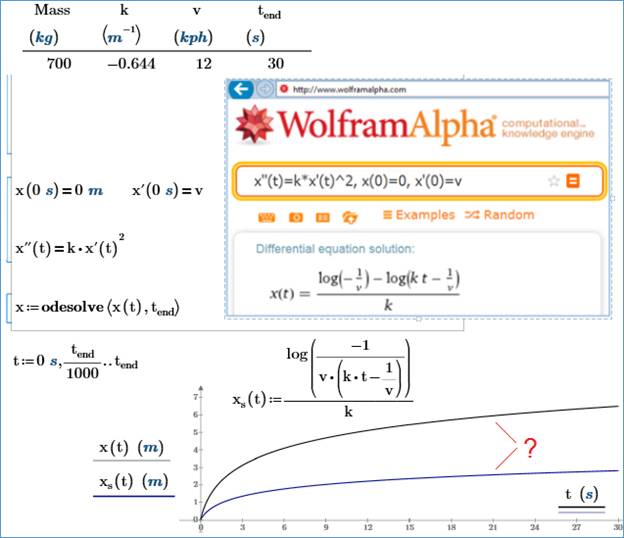
Рис. 22. Графическое сравнение
аналитического и численного решения ОДУ
Почему
на рисунке 22 графики торможения моторной лодки не совпали? Авторы долго ломали
над этим головы, пока не сообразили, что в пакете Mathematica log –
это натуральный логарифм, а в пакете Mathcad – десятичный. Этим и объясняется
различный наклон логарифмических кривых. Если в формуле над кривыми функцию log
заменить на ln
или
log(…, e), то эти две кривые сольются в одну.
По
адресу http://communities.ptc.com/videos/1699 можно видеть авторскую анимацию
решения задачи остановки не моторной лодки, а автомобиля. В соответствующем
дифференциальном уравнении учитываются сила трения качения колес о дорогу и сопротивление
воздуха.
Дифференциальные
уравнения тоже можно разбить на типы. Есть, например, линейные дифференциальные
уравнения, решения которых можно свести к решению алгебраических уравнений. Но
это тема для отдельной статьи.
Выводы
Каждая из рассмотренных
функций «великолепной семерки Mathcad»
обладает своими особенностями и ограничениями. Прежде чем приступать к решению
задачи, следует продумать, какая из этих опций Mathcad приведет к поставленной цели,
причем наилучшим образом.
Школьнику, студенту,
инженеру или ученому необходимо (а в ряде случаев и достаточно) освоить
«великолепную семерку Mathcad»,
особенности численных, графических и аналитических методов решения задач, чтобы
успешно решать на компьютере свои учебные или профессиональные задачи [4].
Литература:
1.
Очков
В.Ф. Физические и экономические величины в Mathcad и Maple (Серия «Диалог с
компьютером»). М.: Финансы и статистика. 2002 (http://twt.mpei.ac.ru/ochkov/Units/Forword_book.htm)
2. Очков В.Ф. Преподавание
математики и математические пакеты // Открытое образование, №2. 2013. С. 23-34
(http://twt.mpei.ac.ru/ochkov/Mathcad-15/OchkovMath-pdf.pdf)
3. Очков В.Ф. Решение алгебраических
уравнений и систем или Ван Гог в среде Mathcad // КомпьютерПресс. № 9. 2001. (http://twt.mpei.ac.ru/ochkov/Carpet/index.htm)
4. Теплотехнические этюды с Excel, Mathcad и Интернет / Под общ.
ред. В.Ф. Очкова. Издательство БХВ-Петербург. 2014. – 336 с. (http://twt.mpei.ac.ru/ochkov/TTMI)