Предел последовательности
![]()
Для любого ![]() существует такое
существует такое ![]() , зависящее от
, зависящее от ![]() , что при всех
, что при всех ![]() справедливо
неравенство
справедливо
неравенство ![]() .
.
Для ![]()
![]() ,
, ![]() , что при
, что при ![]() справедливо
справедливо ![]() .
.
![]() .
.
Задача. Доказать по определению, что ![]()
![]() .
.
Что доказать?
![]() , при
, при ![]() , проще говоря,
, проще говоря, ![]() .
.
Так ли это? Сначала посчитаем: ![]() ;
; ![]() .
.
Стремится ли ![]() к
к ![]() ?
?
Mathcad, Предел последовательности 1,
Предел последовательности 2
Сравните графическую и
числовую иллюстрации. Осторожно!
И всё же нужно доказать
неравенство. Обратимся к графику. Последовательность возрастает и ![]() . Значит нужно найти такое
. Значит нужно найти такое ![]() , что при всех
, что при всех ![]() справедливо
справедливо ![]() , в нашем случае
, в нашем случае ![]()
Mathcad Предел последовательности 3
При ![]()
![]() , при
, при ![]()
![]() , и т.д.
, и т.д.
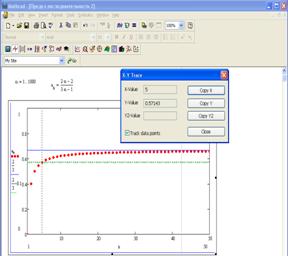
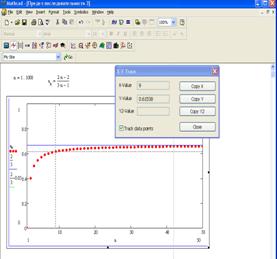
Теперь понятно как найти ![]() :
:
следует решить уравнение ![]() , в нашем случае,
, в нашем случае, ![]() .
.
Mathcad Предел последовательности 4
Впрочем, можно сразу. Mathcad Предел последовательности 5
Посмотрим известные
«замечательные пределы»
Mathcad Предел последовательности 6
Предел функции в точке
![]()
Для любого ![]() (как бы мало оно ни
было) существует такое число
(как бы мало оно ни
было) существует такое число ![]() ,
, ![]() , что для
, что для ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , справедливо
, справедливо ![]() .
.
Другими словами, неравенство ![]() справедливо для
справедливо для ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() .
.
Как и для
последовательностей, эту задачу можно решать графически.
Запишем только эквивалентные
неравенства:
![]() и
и ![]()
Mathcad Предел функции 1
Дифференцирование
Нет проблем!
ТР Дифференцирование, задача 5
ТР Графики Задача 2
Mathcad Производная 1
На занятиях можно разобрать,
попытаться понять задачи 1 и 8 своего варианта из ТР
«Пределы».
Студенты могут решать задачи
5–14 из ТР «Дифференцирование».