|
|
Ко-, три- и квадрогенерация,
или сколько математики в теплотехнике
Энергоэффективность в России —
это охлаждать кондиционером помещение, в котором слишком сильно топят батареи.
www.anekdot.ru
Расчет процессов тригенерации (комплексного последовательного и/или параллельного производства тепла, электроэнергии и холода на одной энергоустановке) требует знания свойств рабочих тел, теплоносителей и конструкционных материалов, задействованных в этих процессах и собранных в различных справочниках и базах данных.
В настоящее время, работая по традиционной технологии,
проектировщик при расчете процессов тригенерации или
отдельных процессов производства тепла, электроэнергии и/или холода вынужден обращаться к бумажным или электронным
источникам информации по свойствам рабочих тел, теплоносителей и конструкционных
материалов. В отдельных случаях проектировщик может
работать и с узкоспециализированными расчетными программами (САПР), в которые "вшиты" модули с нужными свойствами веществ.
Описание таких программ можно найти на сайте www.rosteplo.ru.
Обращение к бумажным или электронным справочникам существенно
замедляет расчет, повышает риск ошибок в них из-за "ручного" копирования
и переноса данных, из-за оплошностей в наборе чисел на клавиатуре компьютера
или из-за промаха в единицах измерения: в справочнике, например, стоят калории,
а расчетная программа требует джоулей или наоборот и т. д. В специализированные
программы часто "вшиты" устаревшие данные с существенными
ограничениями по исходным параметрам, набору рабочих тел и теплоносителей (хладагентов),
например. Очень часто в такие программы "вшиты" не функциональные
зависимости, а простые константы — плотность воды, например, задается как
1000 кг/м3 без учета того факта, что этот термодинамический
параметр самого распространенного рабочего тела и теплоносителя энергетики зависит
от температуры и давления. Температура при этом в старых справочниках может
быть зафиксирована по устаревшей (ITS-68), а не по современной (ITS-90) шкале
(на сайте http://twt.mpei.ac.ru/MCS/Worksheets/
Thermal/T90-T68.xmcd размещен интерактивный
пересчет температур по данным шкалам).
Технология использования "облачных" функций для расчетов лишена многих этих недостатков. В данном этюде она будет проиллюстрирована на несложном примере расчета трубопровода, по которому прокачивается жидкость (теплоноситель, хладагент) для кондиционирования помещений. Расчет ведется в среде универсального пакета Mathcad [1], который в настоящее время широко используется для инженерно-технических расчетов.
Функции по свойствам рабочих тел, теплоносителей и конструкционных
материалов тригенерации расположены в "облаках" —
на внешнем сервере, на который из Mathcad-расчета делаются "облачные"
ссылки. В интернетовских "облаках" обычно
хранят фотографии. Это удобно, надежно, практически не требует каких-либо затрат
или обслуживания. Главное, чтобы у компьютера был выход в Интернет (проводной
или беспроводной), и фотографии можно просматривать с любого места,
с любого компьютера, своего или чужого. Нередко в "облаках" хранится
не только личная, но и служебная информация, а также программы для ее сбора,
размещения, обработки и выдачи. На такую инновационную технологию работы
("облачный" офис) переходят многие инженерные, конструкторские и проектные
бюро, издательства и другие организации, работа которых в настоящее время уже немыслима
без компьютеров. Персонал таких, если так можно выразиться, "облачных"
организаций не занимает отдельного оборудованного помещения с рабочими местами,
локальной компьютерной сетью и сервером, подключенным к Интернету, а работает
на дому, время от времени собираясь в кафе, например, для личного общения,
проведения реальных, а не виртуальных собраний. Все это существенно снижает затраты
на работу и время ее выполнения, не влияя на качество.
Итак, еще раз вспомним, что такое "облачная" функция?
Несложный пример. Необходимо провести гидравлический расчет
сети для подачи тепла или холода потребителям. Теплоноситель — водный раствор
хлористого натрия, который в отличие от чистой воды не замерзает при минусовых
температурах. На эту задачу автора натолкнула его командировка в Баку, где он
встречался со специалистами Азертеплосети (Азеристиликтеджхизад), проводил семинар и рассказывал о
тренажерах для персонала тепловых сетей [2, 3] и о современных технологиях
расчетов на компьютере в области энергетики. Так вот, главный инженер этой
организации посетовал на то, что в Баку в настоящее время строится много современных
многоэтажных жилых домов, но все они, за редким исключением, не подключаются к
существующим теплосетям города, а переводятся на индивидуальное "котловое"
теплоснабжение. Баку — город южный, тем не менее, зимой
в этом городе с Каспия дуют довольно сильные и холодные ветры. Отапливаться
в это время года посредством бытовых электрических нагревателей довольно накладно,
да и электрические сети не выдержат такой пиковой нагрузки, а природный газ
довольно дешев и доступен. Но у построенных новых домов не сооружаются газовые
котельные, снабжающие теплом целый дом или целый микрорайон, как это делается,
например, у нас на новостройках Подмосковья. Бакинские новоселы должны сами
заботиться о своем теплоснабжении. Им приходится "обвешивать" новые
дома мини-котлами, работающими на газе (рис. 17.1).

Рис. 17.1.
Мини-котлы на балконе
многоквартирного дома, обогревающие отдельные квартиры
Такие мини-котлы (в Баку их называют "комби"), предназначенные для индивидуальных коттеджей, устанавливаются на балконах многоквартирных домов, где их можно легко обслуживать, ремонтировать или заменять. На рис. 17.1 также можно видеть компрессорно-конденсаторную часть бытовых кондиционеров (сплит-установок).
Конечно, более рациональным и более "эстетичным" способом теплоснабжения является сооружение около дома, в его подвале или на крыше централизованной газовой котельной. Такими котельными, кстати, оборудованы некоторые новые дома в Москве и в некоторых других городах России. Но в Баку это не делается по ряду причин, главная из которых состоит в том, что строители стараются максимально снизить затраты на сооружение нового дома, предоставляя будущим жильцам возможность (и обязанность) достраивать свой дом самим. В Баку это касается не только "обоев, кафеля и сантехники" (как в Москве), но и теплоснабжения. Кстати, "южнее Баку" — на Ближнем Востоке, в Средней и Южной Азии, в Африке часто отказываются и от централизованного электроснабжения, пристраивая к отдельным домам или устанавливая на балконах многоквартирных домов электрогенераторы с двигателями внутреннего сгорания. С этим явлением хорошо знаком один из авторов этой книги — гражданин Мьянмы.
Такая, грубо говоря, "технико-экономическая глупость",
а мягко говоря, нерациональность наблюдается и в российских городах, где
строятся современные красивые многоквартирные дома бизнес-класса, которые после заселения жильцами обвешиваются
бытовыми кондиционерами. Хотя можно было сразу предусмотреть
в этих домах централизованную установку промышленных кондиционеров или, что
более рационально, систем энергоэффективного
круглогодичного горячего водоснабжения, отопления зимой и охлаждения квартир в
жаркое время года.
Можно, конечно, спорить об экономической целесообразности централизованного тепло- и хладоснабжения современных многоквартирных домов. В Баку, например, холода с ветрами длятся недолго, и многие квартиры "аварийно" отапливаются электричеством, а не горячей водой. Так, кстати, поступают и в Москве в период холодной погоды, когда "батареи еще не включили". Но то, что все эти кондиционеры, мини-котлы (тем более электрические генераторы) уродуют внешний вид дома, ухудшают экологию, это бесспорно. Кондиционеры при этом дополнительно шумят и капают водой на прохожих. Кондиционеры сейчас в некоторых российских городах запрещают вывешивать на фасадах домов. В новых проектах предусмотрены специальные ниши на балконах для бытовых кондиционеров. В некоторых городах Европы, кстати говоря, запрещено открытое или "котловое" сжигание топлива не только для обогрева, но и для приготовления пищи. Нельзя даже приготовить барбекю на углях в садике своего индивидуального дома. Все это нужно делать только с помощью безопасного и "экологичного" электричества, не обращая при этом особого внимания на экономическую сторону вопроса. На сайте по адресу http://twt.mpei.ac.ru/MCS/Worksheets/PTU/Vol-13.xmcd можно найти открытое интерактивное расчетное сравнение систем раздельного и совместного производства электроэнергии и тепла (когенерация). Можно говорить и о квадрогенерации. Некоторые IT-организации имеют мощные серверы с большим автономным электроснабжением с газовыми турбинами или поршневыми двигателями электрогенераторов. Такая организация может производить электроэнергию, тепло, холод и... основной свой продукт — информацию.
Против классической схемы теплоснабжения (ТЭЦ + пиковые водогрейные котлы + тепловые сети) в настоящее время играет и такой факт. Когда тепловые сети проектировались и строились, не было такого интенсивного автомобильного трафика в городах. Теперь же раскопки и ремонт магистральных и местных тепловых сетей приводят к огромным пробкам на дорогах, где стоящие, вернее, "дымящие" машины "пожирают" ту "экономию условного топлива", которую мы получаем за счет централизованного теплоснабжения.
В идеале должно быть так, и это уже осуществляется во многих "продвинутых" странах, заботящихся об энергосбережении, экологии и эстетике построек: на крыше дома, около дома или в его подвале монтируется установка тепло- и хладоснабжения квартир, подключенная к электросети. Само же электричество вырабатывается далеко от дома — на современных мощных электростанциях — тепловых (на органическом или ядерном топливе), гидростанциях, ветровых и пр. При этом домовая установка тепло- и хладоснабжения дооборудуется современными системами энергосбережения — тепловыми насосами, аккумуляторами тепла и/или холода (баки с водой, раствором соли или пласты земли под домом), солнечными коллекторами и пр. В квартиры такого дома подается электричество по проводам и, например, водный раствор поваренной соли — горячий зимой и холодный (с минусовой температурой) летом. Сюда можно еще добавить и централизованный пылесос и централизованную систему удаления отсортированного жильцами мусора, но это мы уже слишком размечтались.
На сайте книги можно найти несколько сетевых, интерактивных,
открытых расчетов, созданных в среде Mathcad и выложенных в Интернете, показывающих
преимущество совместного производства разных видов энергии. На рис. 17.2 и
17.3
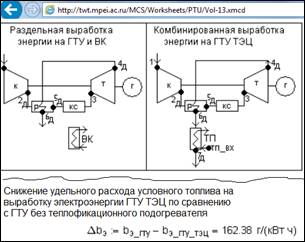
Рис. 17.2.
Расчет экономии топлива на ГТУ ТЭЦ
по сравнению с раздельной выработкой энергии
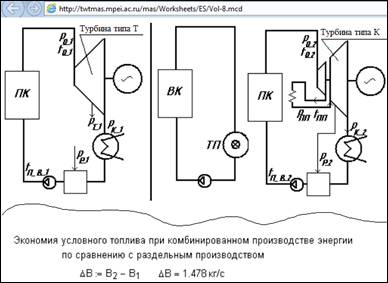
Рис. 17.3.
Определение экономии условного
топлива при теплофикации
на турбинах типа Т (теплофикационная) по сравнению с
раздельной выработкой
одного и того же количества электроэнергии и теплоты
представлены два примера: заголовок (рисунок) расчета и его главный "результирующий" оператор.
Но вернемся к водному раствору соли. Тут, конечно, можно рассматривать и другие теплоносители (фреоны, хладагенты, сведения о свойствах которых есть на описываемом расчетном сервере), но поваренная соль доступна, относительно дешева и, главное, безопасна (нетоксична). Москва, например, стоит на огромном подземном солевом озере, и этот раствор (рапа) московскими энергетиками уже давно используется для регенерации фильтров, применяемых для умягчения добавочной воды теплосетей.
Итак, для расчета сети труб, по которым течет водный раствор хлористого натрия, нужно знать теплофизические свойства этого теплоносителя, в первую очередь его плотность и вязкость.
Для получения этой информации расчетчик может зайти на сайт с адресом www.vpu.ru/mas и сделать там поиск по ключевому слову NaCl. На рис. 17.4 показано, что поиск на данном сервере по ключевому слову NaCl выдал за доли секунды пять ссылок, переход по первой из которых приводит на страницу "Водная химия" (рис. 17.5).
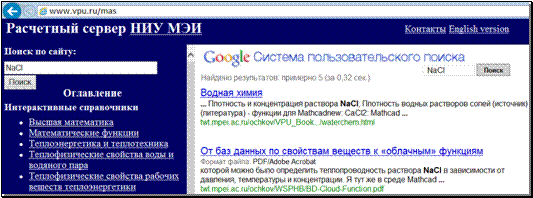
Рис. 17.4.
Расчетный сервер МЭИ — ОИВТ —
Триеру
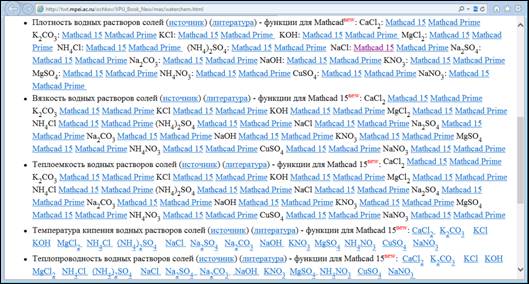
Рис. 17.5.
Страница сайта с теплофизическими
свойствами водных растворов солей
К сайту, показанному на этом рисунке, можно прийти и другим путем: сделать поиск по нужным ключевым словам в среде какой-либо поисковой машины Интернета с помощью Google, например (рис. 17.6).
Рис. 17.6.
Поиск в Google
Кстати, если в Google сделать поиск по ключевому слову "Расчеты в Интернете", то первой позицией в списке выданных ссылок будет ссылка на сайт, отображенный на рис. 17.4. Это говорит о высокой популярности и востребованности расчетного сервера МЭИ — ОИВТ — Триеру.
В поиске, зафиксированном на рис. 17.6, к ключевым словам "плотность водных растворов солей" добавлено слово "Mathcad". Без этого слова поисковая машина выдала бы сайты, где размещены традиционные и никому уже особо не нужные таблицы зависимости плотности от температуры или константы. А нам нужна именно функция для расчетов и такая, чтобы она была доступна ("видима", как говорят программисты) в нашем Mathcad-расчете.
Если к ссылке, отмечающей плотность раствора NaCl (см. на рис. 17.5 третью строку сверху), подвести курсор и нажать правую кнопку мыши, то можно узнать интернет-адрес этой функции — место, где она хранится в "облаках" на внешнем сервере. Эти операции отображены на рис. 17.7.
URL-адрес
(Uniform Resource Locator — универсальный локатор, определитель
местонахождения ресурса), отображенный на рис. 17.7, достаточно
скопировать и перенести в Mathcad-расчет, где необходима функция, возвращающая
плотность раствора NaCl.
В среде Mathcad, как мы уже не раз отмечали, есть очень
удобный инструмент — ссылка из текущего расчета на другой расчет, на
другой файл. После такой ссылки
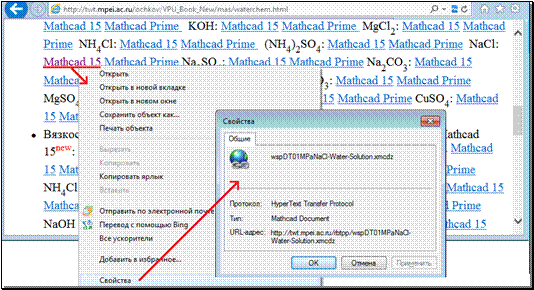
Рис. 17.7.
Определение URL-адреса
"облачной" функции
все пользовательские переменные и функции, определенные в документе, на который сделана ссылка, ставятся видимыми в рабочем документе.
Такие ссылки, как мы уже отмечали, можно делать на файлы, хранящиеся
не только на рабочем компьютере или в локальной компьютерной сети, но в
Интернете,
в "облаках", чем мы сейчас и воспользуемся, решая задачу о
трубопроводе с тепло- и хладоносителем —
водным раствором NaCl.
На рис. 17.8 отображены команды Вставка | Ссылка в среде Mathcad 15, позволяющие сделать ссылку на "облачную" функцию с именем wspDT01MPaNaCl-Water-Solution.xmcdz (D — density/плотность в зависимости от температуры T при давлении 0.1 MPa водного раствора NaCl; о суффиксе wsp рассказано ранее).
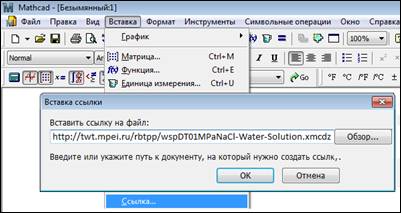
Рис. 17.8.
Ссылка в среде Mathcad 15

Рис. 17.9.
Пример гидравлического расчета в
среде Mathcad 15
На рис. 17.9 показан расчет в среде Mathcad 15 простейшей
системы трубопроводов — определение расходов раствора NaCl на ее отдельных
участках при заданной геометрии труб и заданном напоре насоса. После ввода
исходных данных (геометрические параметры участков труб: длина L, внутренний
диаметр d,
шероховатость, температуры и концентрации водного раствора NaCl) делаются
ссылки на две
"облачные" функции, возвращающие плотность и динамическую вязкость
этого теплоносителя и хранящиеся в "облаках" на сайте, показанном на рис. 17.5
и 17.7. После таких ссылок можно вызывать эти функции,
которые вернули значение плотности (1140.175 kg/m3)
и вязкости (5.085 mPa × s) раствора NaCl с концентрацией 21% и температурой
–15 °С. Следует особо подчеркнуть, что пакет Mathcad может работать с физическими величинами и единицами их измерения
[4], что выгодно отличает его от других компьютерных расчетных программ — от
электронных таблиц Excel и языков программирования
(см. этюд 2).
В расчете, показанном на рис. 17.9, есть две скрытые области. Они раскрыты и показаны на рис. 17.10 и 17.11.
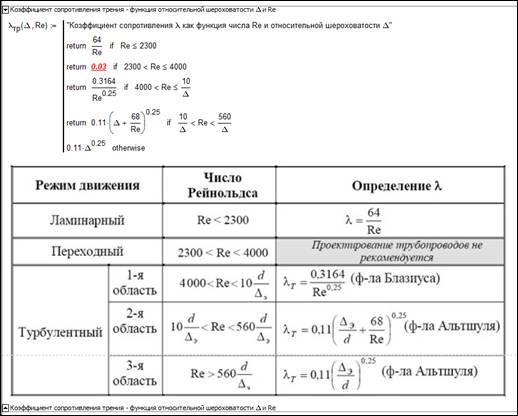
Рис. 17.10.
Расчет коэффициента сопротивления
течению жидкости в трубе
В первой скрытой области (рис. 17.10) хранится функция с
именем lтр
и сама таблица в виде вставленной картинки, по которой эта функция была
создана. Эта функция возвращает значение коэффициента сопротивления жидкости
трением в зависимости от числа Рейнольдса Re
и относительной шероховатости Δ внутренней поверхности труб [5]. В таблице
отмечено, что в диапазоне Re = 2300–4000 (режим, переходный
от ламинарного к турбулентному) коэффициент трения определить
нельзя. Тем не менее, в соответствующей функции проставлено число 0.03. Это
сделано для того, чтобы мог осуществляться итерационный расчет с использованием
этой функции, и об этой "маленькой хитрости" мы еще упомянем далее.
Кстати, на описываемом сайте есть интерактивный расчет (http://twt.mpei.ac.ru/MCS/
Worksheets/Hydro/La-De-Re.xmcd) коэффициента трения в переходной
зоне ("ложка Никурадзе").
Вторая скрытая область расчета, раскрытая и показанная на рис. 17.11, хранит функцию с именем Δh, по которой рассчитывается перепад (потеря) давления в трубопроводе в зависимости от его длины L, внутреннего диаметра d и объемного расхода жидкости q. В этой функции программные строки представляют собой матрицу с двумя столбцами и одной строкой ("горизонтальный" вектор), у которой первый элемент — это комментарий, а второй — формула. Если бы у труб была различная шероховатость (отказ от одного из допущений), то функцию Δh следовало бы дополнить еще одним аргументом Δ. Функция Δh использует функцию с именем λтр, показанную на рис. 17.10. Это стандартные формулы гидродинамики, которые можно найти в справочниках или в Интернете. Мы их уже использовали в предыдущем этюде. Таблица, показанная на рис. 17.10, найдена именно в Интернете, скопирована и перенесена в виде рисунка в наш расчет как некий комментарий. В этой таблице значение lтр для переходного режима течения жидкости не определено. Но в функции lтр оно равно 0.03. Это, повторяем, сделано для того, чтобы можно было вести итерационный расчет при решении системы алгебраических уравнений (см. рис. 17.9). В справочниках и в Интернете приводится несколько именных и безымянных разноречивых формул для расчета коэффициента трения жидкости в зависимости от режима ее течения и шероховатости поверхности труб. Но это разночтение в какой-то мере нивелируется неопределенностью самого понятия — "шероховатость".

Рис. 17.11.
Расчет перепада давления на
участках трубопровода
Функция с именем Δh (рис. 17.11) возвращает потерю напора
жидкости на участке трубопровода в зависимости от длины трубы L, ее
внутреннего диаметра d и объемного расхода жидкости q.
Это, так сказать, "внутренние" аргументы функции Δh.
"Внешними" аргументами функции Δh, не перечисленными в списке ее аргументов, являются
шероховатость внутренней поверхности трубы Δ, плотность жидкости ρ
и ее динамическая вязкость m. В функции Δh фигурируют и две константы: отношение длины
окружности к ее диаметру π и ускорение свободного падения g.
Вторую константу константой можно считать условно, т. к. она незначительно,
но зависит от широты местности и от высоты над уровнем моря. На сайте автора
есть онлайн-расчет ускорения свободного падения в зависимости
от вышеуказанных параметров местности. Но следует также не
забывать, что трубная система может быть смонтирована не только на Земле, но и
на орбитальной станции или даже на Луне или Марсе, где значение g
существенно отличается от величины 9.81 m/s2.
Это мы уже отмечали в этюде 16. Так что функция
Δh в
принципе должна иметь следующий список аргументов: L, d, q,
Δ, r,
m,
g.
Но мы его сократили, изъяв из него переменные, общие для всех участков труб.
После определения нужных четырех функций: двух
"облачных" rNaCl
и mNaCl
(см. рис. 17.9) и двух пользовательских lтр
(см. рис. 17.10) и ΔН
(см. рис. 17.11) несложно решить поставленную задачу, воспользовавшись инструментом
решения системы нелинейных алгебраических уравнений, встроенным в Mathcad:
ключевым словом Given
(Дано) и функцией Find (Найти) — см. рис. 17.9.
При решении нелинейных систем алгебраических уравнений в среде Mathcad необходимо,
повторяем, дать первое приближение к искомым величинам. Если говорить о задаче,
показанной на рис. 17.12, то это значение напора насоса и значения объемных
расходов жидкости на отдельных участках трубопровода.
Система уравнений — это баланс расходов в тройниках (q1 = q2 + q3) и баланс перепадов давлений на отдельных замкнутых участках сети. Локальные сопротивления тройников, гибов труб, запорной и регулирующей арматуры в нашем расчете не учитываются (еще одно допущение). Кроме того, сделано еще одно существенное допущение: наши трубы лежат на горизонтальной плоскости и перепады высот не учитываются. Но эти ограничения несложно снять.
Пакет Mathcad нашел такие значения переменных, что при их подстановке в уравнения с заданными значениями напора насоса и массовых расходов жидкости правые и левые части уравнений отличаются незначительно или совсем не отличаются. Это подтверждено проверкой, которая показана в конце рис. 17.9. Подчеркиваем особо, что задача решалась не аналитическими, а численными (приближенными) методами, заложенными в функцию Find.
Прямое использование "облачных" функций через
ссылки на них, как это показано на рис. 17.9, имеет одно существенное
ограничение. Дело в том, что некоторые
организации ограничивают или вовсе блокируют прямой выход своих сотрудников в
Интернет с рабочих станций, что мы уже отмечали в этюде 1.
Это делается и в целях безопасности, и для того, чтобы
сотрудники не отвлекались от основной работы, заходя на новостные и развлекательные
сайты, общаясь с друзьями в социальных сетях и т. д. На компьютере, отключенном
от Интернета, расчет, показанный на рис. 17.9, работать не будет, а
ссылки, включенные в него (http://...),
станут красными (см. рис. 4.3 в этюде 4), что
будет указывать на аварийную ситуацию. В этом
случае можно рекомендовать сделать следующее.
Администратор локальной компьютерной сети ("сисадмин") в организации, где заблокирован выход в Интернет с рабочих станций рядовых сотрудников, может по просьбе конкретного расчетчика скачать нужную функцию, проверить ее на отсутствие вирусов и "троянов" и разместить в локальной сети или на некоторых рабочих станциях. На рис. 17.7 можно видеть команду Сохранить объект как..., позволяющую сделать это. На скачанную, проверенную и размещенную в организации функцию можно опять же ссылаться, а можно просто встраивать ее в расчет, что в отличие от относительных ссылок не будет приводить к сбою при переносе расчета с одного компьютера на другой. (Ссылки, показанные на рис. 17.9, абсолютные, а не относительные.)
На рис. 17.12 показан расчет несколько усложненной трубной системы в среде более новой версии Mathcad — Mathcad Prime. Исходной величиной расчета является расход жидкости через насос q1, а искомой величиной — его напор ΔН, выраженный в метрах и (после соответствующего пересчета) в атмосферах. Еще одно отличие расчета на рис. 17.12 от расчета на рис. 17.9 в том, что в среде Mathcad Prime применяется новый инструмент Блок решения, а не тандем ключевого слова Given и функции Find, как в среде Mathcad 15. На рис. 17.13 отображена проверка решения.
Систему труб, изображенную на рис. 17.12, можно и дальше усложнять, добавлять в расчет новые уравнения, отображающие балансы потоков и суммы перепадов давления по отдельным замкнутым кольцевым участкам. Но скоро окажется, что Mathcad не сможет решить систему уравнений. Бессильны тут будут и специализированные пакеты, нацеленные именно на решение таких систем уравнений. Нужно будет использовать специальные "хитрые" методы решения таких задач и узкоспециализированные программные средства, созданные именно для расчета трубопроводов. Но и в этих программах нужны будут сведения по свойствам жидкостей, доступные по технологии "облаков", которая была описана в данном этюде и в других местах книги.
Блок решения алгебраических уравнений в среде Mathcad может возвращать не только конкретные численные значения, но и создавать функции пользователя, по которым можно строить графики. Сейчас мы этим воспользуемся и построим график зависимости расхода жидкости в нашей гидравлической системе (см. рис. 17.12) от напора насоса. Для этого в расчет, показанный на этом рисунке, достаточно внести небольшие изменения, отображенные на рис. 17.14.
Во-первых,
в расчете нужно убрать оператор задания начального приближения
к решению по напору насоса. На рис. 17.15 этот оператор зачеркнут.
Во-вторых, функцию Find необходимо присваивать не вектору,
как на рис. 17.15, а функции пользователя с именем q.
Эта функция не простая, а функция-вектор. Выделив ее первый элемент (в данном
расчете системная переменная ORIGIN
равна единице), можно построить график расхода жидкости через насос в
зависимости от его напора. Разрывы на линии означают, что на данных участках
пакет Mathcad не смог решить систему нелинейных алгебраических уравнений.
Пакет Mathcad имеет инструменты для решения не только систем нелинейных алгебраических уравнений (см. рис. 17.7 и 17.12), но и для решения систем линейных уравнений.
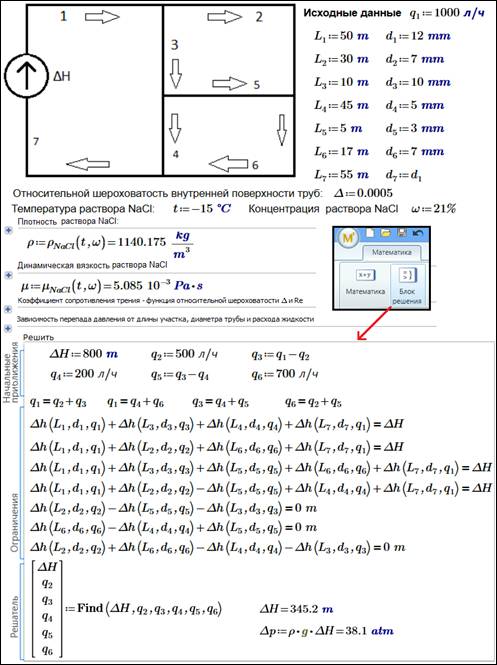
Рис. 17.12.
Пример гидравлического расчета в
среде Mathcad Prime

Рис. 17.13.
Проверка гидравлического расчета в
среде Mathcad Prime
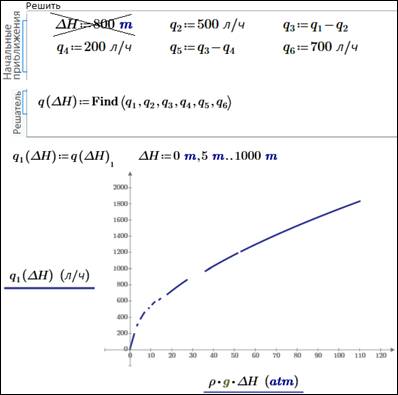
Рис. 17.14.
Построение графической зависимости
расхода жидкости через насос
от его напора
Наша задача о трубопроводной сети имеет прямой аналог в электротехнике: насос — это источник электрического тока (генератор, аккумулятор и др.) с некой электродвижущей силой (ЭДС), выраженной в вольтах, а участки трубопроводов, задвижки, тройники, угольники и пр. — это электрические сопротивления, которые в отличие от "гидравлических сопротивлений" мало зависят по своим значениям (омы) от силы тока. Поэтому решение типовой задачи электротехники — нахождение значений тока на отдельных участках цепи в зависимости от заданных значений локальных сопротивлений и ЭДС сводится к решению системы линейных алгебраических уравнений. На рис. 17.15 показана "переделка" нашей гидравлической задачи, изображенной на рис. 17.12, в электротехническую задачу.
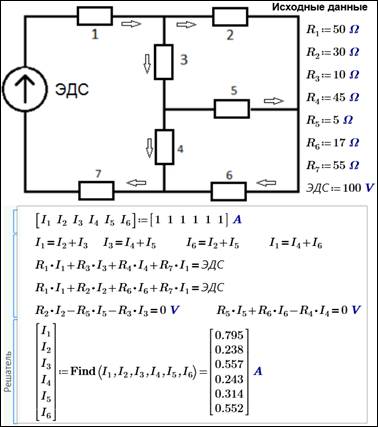
Рис. 17.15.
Пример электротехнического расчета
в среде Mathcad Prime
На рис. 17.15 показано решение электротехнической задачи блоком Решатель: вводятся начальные приближения к решению: всем шести искомым значениям тока присваивается один ампер. Но можно давать и другие значения. Выбор этих значений — важный этап решения задачи. Пакет Mathcad иногда не может решить систему и просит изменить начальные приближения. Инженер, решающий на компьютере свою задачу, должен приблизительно знать, какое решение ему нужно, и давать первое приближение вблизи этой точки. Далее в расчете на рис. 17.15 записываются уравнения баланса токов (первый закон Кирхгофа) и баланса "энергий" по отдельным замкнутым ветвям электрической сети (второй закон Кирхгофа). Функция Find возвратила значение шести токов, дающих приближенное решение исходной системы. У нас в задаче восемь уравнений и шесть неизвестных. Задача, следовательно, является переопределенной[1], т. к. в ней число уравнений превышает число неизвестных. В принципе, тут два уравнения лишние. Но можно добавить еще пару уравнений[2], применив второе правило Кирхгофа к замкнутым ветвям электрической цепи ЭДС-R1-R3-R5-R6-R7 и ЭДС-R1-R2-R5-R4-R7. Задача при этом будет еще более переопределена, но решение при этом останется прежним. Решение, показанное на рис. 17.15, вполне может устроить пользователя, если он будет уверен в единственности решения, т. е. в возможности искать это решение любыми доступными способами. Но и здесь требуется уточнить, о единственности какого решения идет речь: решения поставленной электротехнической задачи или решения конкретной системы линейных алгебраических уравнений, которая в общем случае может плохо описывать физическую модель, поскольку имеет варианты. Кроме того, смущает то, что приходится задавать начальные приближения к решению[3]. Обычно это делается тогда, когда у системы несколько решений, а нужно найти только одно. Пользователь должен хотя бы примерно знать, сколько решений будет у поставленной реальной задачи и какую тактику при решении конкретной задачи он должен использовать. Несколько решений бывают у нелинейных систем, а наша система, повторяем, линейная. У такой системы обычно единственное решение, но есть случаи, когда решений нет или их бесконечное множество. Сейчас мы покажем, как можно в линейной системе алгебраических уравнений детерминировать эти три случая.
На рис. 17.16 показано решение нашей "гидросетевой" задачи одним из инструментов Mathcad, предназначенным для решения систем линейных алгебраических уравнений — функцией lsolve (l — линейный, solve — решить).
В верхней части рис. 17.16 записаны наши уравнения, вытекающие из первого и второго законов (правил) Кирхгофа, дополненные "нулевыми" слагаемыми и коэффициентами так, чтобы получилась система линейных уравнений в ее классическом написании: коэффициенты при неизвестных, сами неизвестные и правые части уравнений. После этого можно сформировать матрицу коэффициентов при неизвестных М и вектор свободных членов v. Функция lsolve вернула нам решение, повторяющее решение на рис. 17.15, но без всяких "начальных приближений", которые нас смущали.

Рис. 17.16.
Решение переопределенной системы
линейных алгебраических уравнений
в среде Mathcad Prime
Из нашей системы можно убрать два лишних уравнения[4],
как мы уже отметили
ранее. После этого матрица М станет
квадратной, и у нее можно будет подсчитать детерминант (определитель) и инвертировать
ее (найти обратную матрицу). Обратную матрицу можно умножить на вектор
свободных членов и... получить решение задачи. Вот тут-то и пригодятся нам
знания линейной алгебры, которые мы приобрели в институте! На рис. 17.17 решается
"классическая" система шести линейных алгебраических уравнений с
шестью неизвестными "классическим" способом — векторным
умножением инвертированной (обратной) матрицы коэффициентов при неизвестных на
вектор свободных членов. Убедиться в том, что мы имеем единственное решение,
помогает функция rank,
возвращающая ранг квадратной матрицы M и расширенной
матрицы M1. Теорема Кронекера — Капелли гласит, что "система линейных алгебраических
уравнений совместна тогда и только тогда, когда ранг ее основной матрицы равен
рангу ее расширенной матрицы, причем система имеет единственное решение, если
ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше
числа неизвестных".
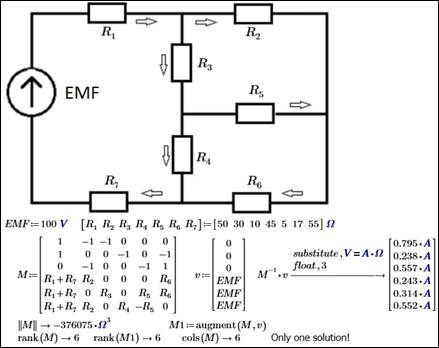
Рис. 17.17.
Анализ и решение
"классической" системы линейных алгебраических уравнений в среде
Mathcad Prime с привлечением азов линейной алгебры
В нашей системе шести линейных алгебраических уравнений с шестью неизвестными (см. рис. 17.17) записаны три первых правила Кирхгофа и три вторых правила Кирхгофа. Если эту пропорцию нарушить, записать, например, два первых правила Кирхгофа для двух "тройников" и четыре вторых правила Кирхгофа для четырех замкнутых петель, то можно получить неверное решение[5]. И самое неприятное будет то, что это решение будет очень похоже на истинное[6]. Если нашу модель изменить (записать два, а не три первых правила Кирхгофа и четыре, а не три вторых правила Кирхгофа), то ранги новой основной и новой расширенной матриц при этом станут равны 5 (см. рис. 17.18), а не 6 (см. рис. 17.17), что будет сигналом об ошибке в решении, т. к. наша система имеет 6 неизвестных (см. выше теорему Кронекера — Капелли). Вывод такой: для решаемой задачи математическая модель, адекватная физической, содержит ровно шесть линейно независимых уравнений, которые можно правильно выделить из бóльшего (избыточного) числа непротиворечивых уравнений, используя либо математический подход (вычисление ранга матрицы и выделение базисного минора), либо физический подход (определение физической значимости каждого из уравнений). Первый требует хороших знаний общей теории решения систем линейных алгебраических уравнений, второй помимо знания теории цепей требует хорошо развитой интуиции и навыка в решении подобных задач. Но если не ставить своей целью уменьшение количества уравнений, то решение переопределенной алгебраической системы можно просто поручить компьютеру.

Рис. 17.18.
Анализ неправильно составленной
системы линейных алгебраических уравнений
Разбор систем линейных уравнений в нашем "нелинейном" этюде неслучаен. Исходная гидравлическая система — нелинейная, но ее можно временно линеаризировать, т. е. принять грубое допущение о том, что сопротивление трубопроводов не зависит от расхода жидкости. После этого можно будет решить такую систему линейных уравнений с помощью функции lsolve (см. рис. 17.16) или через умножение обратной матрицы коэффициентов при неизвестных на вектор свободных членов (см. рис. 17.17). Для полноты картины сюда можно добавить и метод Гаусса, который, кстати, теоретически легко и однозначно справляется с любым числом уравнений и неизвестных. Полученное решение затем следует использовать как первое приближение для функции Find, приложенной уже к нелинейной исходной задаче о сети трубопроводов (см. рис. 17.12). Кстати говоря, наша задача об электрической цепи (см. рис. 17.15–17.17) тоже нелинейна. При прохождении электрического тока сопротивление нагревается. А значение электрического сопротивления, как и значение термического сопротивления (см. этюд 21), существенно зависит от температуры. При небольшом электрическом токе (при незначительном нагреве сопротивления) эти изменения можно игнорировать, но в электротермических установках этого делать нельзя. Можно с помощью мегомметра замерить сопротивление лампочки накаливания, поделить квадрат напряжения электрической сети на измеренное значение сопротивления вольфрамовой нити и... не получить значение мощности лампочки, пропечатанное на ней. Электрическое сопротивление вольфрама резко растет при его нагреве. В противном случае вольфрамовая нить лампочки сразу бы перегорала при ее включении. Интересная задача на стыке тепло- и электротехники: рассчитать изменение во времени температуры нити накаливания лампочки при ее включении или выключении, а также при скачках напряжения. Эта задача относится к классу задач для дифференциальных уравнений, которые мы рассмотрим в следующем этюде. Аналог этой нестационарной теплообменной задачи показан на рис. 18.10 в этюде 18.
Вернемся ко второму названию этюда. Иммануилу Канту приписывают такое изречение: "В каждой естественной науке заключено столько истины, сколько в ней есть математики". В Московском энергетическом институте, где автор читает курс "Информационные технологии", студентам-первокурсникам параллельно читают курс высшей математики, содержащий разделы, относящиеся к линейной алгебре (см. ранее) и математическому анализу. На последующих семестрах читают также и численные методы математики. Без этой триады невозможно освоение теплотехники — термодинамики и тепломассообмена.
Азы линейной алгебры, а точнее, матричного исчисления, с
матрицами — исходными и инвертированными, рангами матриц и пр. мы рассмотрели
на примере решения задачи, отображенной на рис. 17.17. В функцию Find
(см. рис. 17.12–17.14) заложены различные методы численного
решения систем линейных и нелинейных алгебраических уравнений. Их список можно
увидеть, если в среде Mathcad 15 нажать правую кнопку мыши на функции Find.
Теперь мы рассмотрим азы математического анализа на
примере опять же "теплотехнических" задач. Правда, первая из
рассмотренных далее задач о форме подводной лодки не относится к математическому
анализу, т. к. не содержит ни дифференциального, ни интегрального исчислений,
ни рядов, ни векторного анализа. Это стереометрическая задача элементарной математики.
Она показывает, что системы алгебраических уравнений могут быть не только переопределенными
(см. ранее), но и недоопределенными. Так случается, например, тогда, когда
число уравнений меньше числа неизвестных. Такую задачу можно увидеть в описании
еще одного "гидравлического" устройства —
в геометрии подводной лодки "Наутилус" — "героине" романов
Жюля Верна "Двадцать
тысяч лье под водой" и "Таинственный остров". Вот что можно
узнать из разговора капитана Немо с профессором Аронаксом
о размерах этой подлодки: "Вот, господин Аронакс,
чертежи судна, на котором вы находитесь. Судно представляет собой сильно
удлиненный цилиндр с коническими концами. <...> Площадь его равняется
одной тысяче одиннадцати и сорока пяти сотым квадратных метров, объем равен
одной тысяче пятистам и двум десятым кубических метров; короче говоря, корабль,
полностью погруженный в воду, вытесняет тысячу пятьсот и две десятых кубических
метров, или тонн, воды".
На рис. 17.19 показано решение задачи о размерах
подводной лодки "Наутилус"
в среде Mathcad с помощью оператора solve символьной математики пакета.
Этот оператор возвращает в данной задаче не конкретные числовые значения, а
формирует выражения, которые затем отображаются на графике. Дело в том, что недоопределенные системы алгебраических уравнений могут
иметь множество решений. В нашем случае размеры субмарины (длины H и L) при заданной
геометрии подводной лодки, известных ее объеме и
площади поверхности зависят от радиуса сечения цилиндрической части R. Кроме
того, сама система наших двух нелинейных уравнений имеет два решения. Поэтому
оператор solve
вернул нам не вектор, а матрицу, состоящую из двух строк (длины H и L) и
двух столбцов (два решения задачи). На рис. 17.19 эта матрица показана
только частично. Здесь же эти зависимости отображены графически в области
значений R
от 0 до 13 м. Если допустить, что ра-
диус R
сечения цилиндрической части субмарины равен, например, 3.13 м, то длина
ее конических частей (носа и кормы) H
будет равна 5.627 или 0.823 м, а длина центральной цилиндрической части L —
44.991 или 48.194 м. Первый вариант (H = 5.627 м и L = 44.991 м)
представляется наиболее вероятным, т. к. при втором решении (H = 0.823 м
и L = 48.194 м)
нос лодки был бы слишком тупым, что увеличивало бы сопротивление воды при движении
лодки[7]
и не соответствовало бы изображениям "Наутилуса" в иллюстрациях к книгам
Жюля Верна.
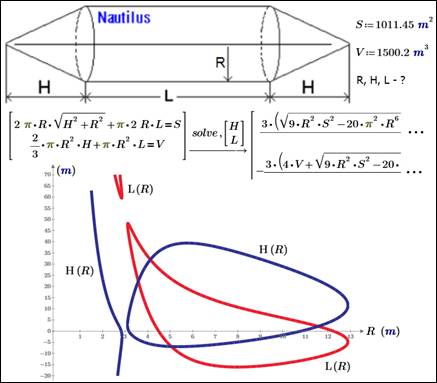
Рис. 17.19.
Графико-аналитическое решение недоопределенной системы
нелинейных алгебраических уравнений
Наши рассуждения о недо- и переопределенности систем алгебраических уравнений с точки зрения математиков несколько надуманные. Просто в ранних версиях пакета Mathcad не было встроенной функции lsolve, и системы линейных алгебраических уравнений приходилось решать только умножением инвертированной матрицы коэффициентов при неизвестных на вектор свободных членов. Матрица коэффициентов при неизвестных при этом могла быть только квадратной. Анонсирование функции lsolve в новой версии Mathcad особо подчеркивало, что теперь можно решать недо- или переопределенные системы алгебраических уравнений.
Теперь мы рассмотрим азы применения математического анализа к решению задачи, также связанной с нашими гидравлическими (тепловыми) сетями.
В тепловой сети приходится восполнять потери водного теплоносителя,
который хранится в баке добавочной воды. Этот бак обычно имеет форму прямого
кругового цилиндра. А каковы его пропорции? Если у
цилиндрического бака с верхней крышкой задан объем (30 м3, например),
то можно найти значения радиуса основания цилиндра r
и его высоты h,
при которых площадь полной поверхности бака будет минимальна. А значит, будет
минимален расход металла на изготовление бака и материала на его теплоизоляцию[8].
Эта задача решена на рис. 17.20 с помощью "численной" функции
Mathcad — функции minimize с опорой опять же на начальные
приближения — по 3 м для радиуса и высоты цилиндра. Почему именно
по 3 м? (См. ранее наше замечание о выборе точки начального приближения к
решению.)

Рис. 17.20.
Численное решение задачи об
оптимальном размере цилиндра
Но тут можно вспомнить математический
анализ и решить задачу о цилиндре не для конкретного заданного его объема (инженерный подход к задаче),
а в ее общей постановке (математический подход к задаче), и доказать, что у любого
прямого кругового цилиндра
с минимальной площадью полной поверхности диаметр основания будет равен его высоте. Решение
такой общей задачи
средствами символьной математики Mathcad показан на рис. 17.21 через поиск
значения аргумента, при котором производная функции будет равна нулю.
На форуме http://communities.
ptc.com/message/196860 даны численные и аналитические решения
данной оптимизационной задачи для емкостей (геометрических тел) других форм —
цилиндра без
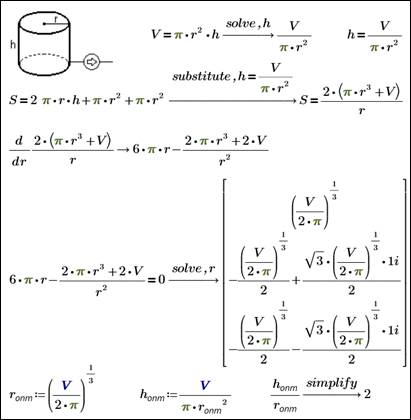
Рис. 17.21.
Аналитическое решение задачи об
оптимальном размере цилиндра
верхней крышки, конуса с верхней крышкой и без нее, конуса с полусферой в основании ("мороженое в рожке") и др.
Мы ранее упомянули инженерный и математический подходы к
решению задач.
В этой связи можно вспомнить такую историю. Воздушный шар вырвался из облаков. Летящие увидели на земле человека и закричали: "Где мы
находимся?" "Вы находитесь в корзине воздушного шара", — таков
был ответ. Его дал математик. Только от математика можно услышать совершенно
точный и совершенно бесполезный ответ[9].
Условно считается, что использование численной математики Mathcad — это
инженерный подход к решению задачи, а использование символьной математики —
это математический подход. Задачу (и не только теплотехническую), конечно,
нужно начинать решать в ее общей постановке и искать следует общее решение. Но
очень часто бывает так, что общее решение оказывается "абсолютно точным и
абсолютно бесполезным". Символьная математика часто выдает либо все ответы
(см. рис. 17.21), из которых надо еще уметь
выбрать нужный, либо совсем не выдает ответа. С численной математикой можно как
бы подтолкнуть компьютер к нужному решению, задав правильное приближение к нему[10].
Хорошо, конечно, помнить или доказать самому себе еще раз (см.
рис. 17.21), что у прямого круглого цилиндра площадь полной поверхности минимальна при
равенстве
диаметра основания высоте. Но решая конкретную задачу о проектировании ем-
кости для хранения воды с заданным объемом, проще сразу перейти к численным
методам и минимизировать целевую функцию с двумя неизвестными r
и h
(см. рис. 17.20). Однако можно немного подумать вместе с компьютером и сообразить,
что у этой задачи одна неизвестная величина — радиус основания цилиндра,
например. А у функции одного аргумента минимум можно найти и на графике (рис. 17.22).
Но можно ограничиться и решением с двумя неизвестными величинами[11]
(см. рис. 17.18), опираясь на KISS-принцип: keep it simply,
stupid — делай это проще, дурачок!
Главное тут — умелое сочетание применения аналитических и численных
методов решения задач и... привлечение математиков для их критического анализа.
Приведу конкретный пример. Автор этой книги послал данный этюд одному хорошему
математику, который подправил текст и дал ценные замечания, показанные в
сносках. Потом этот математик подправил другие этюды и стал соавтором книги. Ну
и саму математику нужно изучать, хотя бы с помощью Mathcad
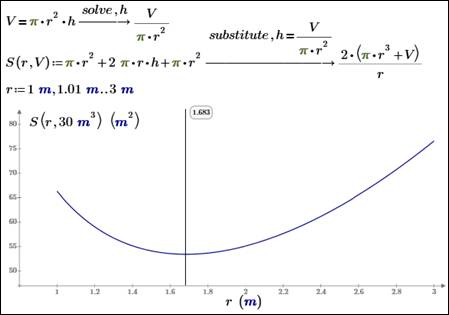
Рис. 17.22.
Сочетание аналитических и
графических методов решения задачи
об оптимальном размере цилиндра
[7]. Задачу о размерах цилиндра легко можно решить в среде MS Excel с помощью надстройки Поиск решения (см. рис. 7.7 в этюде 7).
Вернемся к первому названию этюда — к квадрогенерации. Дополнительная генерация информации на
тепловой электростанции, о которой мы писали ранее, — это, конечно, чистой
воды экзотика. Но электростанции, производя тепло- и электроэнергию, могут быть
полезными и в других сферах. На некоторых электростанциях Западной Европы,
например, сжигают мусор. И не только тот, который образуется в результате
текущей жизнедеятельности города и который нельзя утилизировать другими
способами, но и "старый" мусор, хранящийся на так называемых
"мусорных полигонах" и представляющий собой реальную экологическую
угрозу, например, подземным водам. Другая "полезность" электростанции
может заключаться
в следующем. Большие города Центральной и Северной России зимой имеют проблемы
с утилизацией снега, убираемого с дорог. Этот снег не простой, а сильно загрязненный
противогололедными реагентами, которыми дороги
посыпают и поливают после каждого снегопада. Наши городские ТЭЦ могли бы этот
снег зимой складировать на своей территории, а летом растапливать, выделяя из
него противогололедные реагенты для последующего
нового использования будущей зимой. Очищенную воду можно использовать для подпитки
энергоблоков и систем охлаждения конденсаторов. КПД такой станции, кстати
говоря, повысился бы за счет снижения температуры охлаждающей воды, поступающей
в конденсатор [8, 9].
Литература
1. Очков В. Ф. Mathcad 14 для студентов и инженеров: русская версия. — СПб.: БХВ-Петербург, 2009. — 512 с. URL: http://twt.mpei.ac.ru/ochkov/Mathcad_14/RusIndex.html.
2. Очков В. Ф., Орлов К. А., Кондакова Г. Ю., Очков А. В. Тренажер диспетчера тепловой сети // Энергетик. — 2009. — № 4. — С. 38–41. URL: http://twt.mpei.ac.ru/ochkov/trenager/ThermoNet/page38.png (39, 40 и 41).png.
3.
Очков В. Ф., Мищеряков С. В., Орлов
К. А. и др. Тренажер для подготовки персонала тепловых
сетей // Новое в российской электроэнергетике. — 2007. — № 1. —
С. 33–43. URL:
http://twt.mpei.ac.ru/ochkov/trenager/ThermoNet/Article_NRE.html.
4. Очков
В. Ф. Физические и экономические величины в Mathcad и Maple. —
М.: Финансы и статистика, 2002. — Серия "Диалог с компьютером". URL:
http://twt.mpei.ac.ru/ochkov/Units/Forword_book.htm.
5. Очков В. Ф., Орлов К. А., Чжо Ко Ко, Анохин Д. А. "Облачные" функции для инженерных расчетов водоснабжения // Водоснабжение и канализация. — 2012. — № 9, 10. — С. 68–74. URL: http://twt.mpei.ac.ru/GDHB/CloudFunction.pdf.
6.
Очков В. Ф. Преподавание математики и
математические пакеты (макет) // Открытое образование. — 2013. —
№ 2. — С. 23–34. URL:
http://twt.mpei.ac.ru/ochkov/Mathcad-15/OchkovMath.pdf.
7. Плис
А. И., Сливина Н. А. Mathcad. Математический практикум для инженеров
и экономистов: учеб. пособие. —
2-е изд. перераб. и доп. — М.: Финансы
и статистика, 2003.
8. Очков
В. Ф. Снег в мегаполисе и энергетика // Энергосбережение и водоподготовка. —
2005. — № 1. URL:
http://twt.mpei.ac.ru/ochkov/Snow/index.html.
9. Очков
В. Ф. Снег в большом городе // Водоочистка, водоподготовка,
водоснабжение. — 2010. — № 3 (27). — C. 72–74. URL: http://twt.mpei.ac.ru/ochkov/Snow/index-vvv.html.
