Публикация в Интернете теплофизических свойств веществ: проблемы и решения при работе с таблицами

Очков В.Ф.

Журнал "Труды Академэнерго", №2, 2009

Изложены методика и инструментальные средства публикации в Интернете интерактивных расчетов по теплофизическим свойствам веществ.

Таблицы теплофизических свойств веществ в справочной литературе, как правило, публикуются в двух видах:

• теплофизические свойства веществ на линии насыщения или при определенном (чаще всего атмосферном) давлении: таблицы с «боковиком» – дискретные значения температуры и последующими столбцами – значениями свойств;

• теплофизические свойства веществ в однофазной области: таблицы с «боковиком» – дискретные значения температуры и «шапкой» – дискретные значения давления.

Данные первого вида, как правило, укладываются в полностью заполненную таблицу, где в первом столбце («боковике»), как уже отмечено, хранятся значения температуры, а в последующих – соответствующие этим значениям температуры значения теплофизических свойств веществ: давление насыщение[1], плотность, удельная изобарная теплоемкость, удельная энтальпия, удельная энтропия, вязкость (кинематическая и динамическая), теплопроводность, число Прандтля и т.д. Табл. 1 – это типичная подобная таблица, взятая из [1]. Она хранит теплофизические свойства конденсата Карачаганакского газового месторождения (http://ru.wikipedia.org/wiki/Карачаганакское_месторождение).

Табл. 1. Типичная таблица по свойствам вещества на линии насыщения

Иногда данные первого вида в справочной литературе представлены не полностью заполненными таблицами: плотность дана, например, в одном температурном интервале или при одних значениях температуры, а теплопроводность в другом интервале или при других значениях температуры. Но эта особенность не является критичной как в случае с данными второго вида (см. ниже): при обработке таких «разноинтервальных» данных из таблицы изымаются пары векторов (температура-плотность, температура-теплопроводность и т.д.) одинаковой длины для дальнейшей сепаратной работы с ними – интерполяции или аппроксимации.

Данные второго вида, как правило, размещаются в частично заполненных таблицах, где прочерки в ячейках означают, что при данных значениях температуры («боковик» таблицы) и давления («шапка» таблицы) рассматриваемое вещество находится в ином агрегатном состоянии. Табл. 2 – это типичная подобная таблица, взятая также из [1] и соответствующая тому же веществу, вернее смеси веществ (углеводородов) – конденсат Карачаганаксого газового месторождения.

Табл. 2. Типичная частично заполненная таблица по свойствам вещества в однофазной области

Данные, показанные в табл. 2, в нижнем левом углу отсечены невидимой линией, дискретные координаты которой хранятся в первых двух столбцах табл. 1 (температура и давление насыщения). В [1] приведены и другие таблицы, схожие по виду с табл. 2, но хранящие данные по иным теплофизическим свойствам, перечисленным в «шапке» табл. 1.

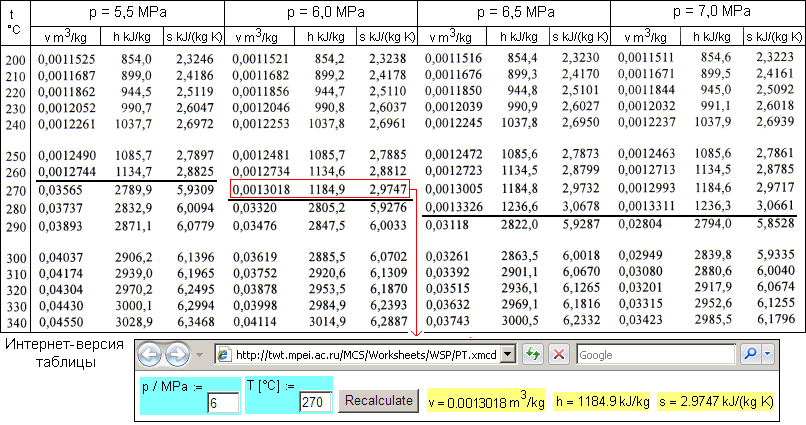
Если же таблица второго вида заполнена полностью и при этом «накрывает» линию насыщения (фазового перехода), то в такой таблице ступенчатой линией отмечается граница фазового перехода «жидкость – газ (кипение – конденсация)», «жидкость – твердое вещество (плавление – кристаллизация)» или «твердое вещество – газ (возгонка – сублимация)». Типичной полностью заполненной таблицей второго вида со ступенчатой линией, отделяющей воду от водяного пара является таблица термодинамических свойств воды и водяного пара в однофазной области (табл. 3), взятая из [2].

Табл. 3. Фрагмент типичной полностью заполненной таблицы по свойствам вещества в однофазной области со ступенчатой линией фазового перехода

В настоящее время в связи с развитием технологии «облачных» вычислений[2] и с учетом того факта, что компьютер с выходом в Интернет на столе инженерно-технического работника все чаще и чаще заменяет традиционный бумажный справочник с «мертвыми»[3] формулами, графиками, таблицами, стало возможным переносить таблицы, подобные тем, которые показаны выше, на специальные расчетные сайты Интернета [3-5]. Так внизу табл. 3 читатель может увидеть ее Интернет-версию[4], размещенную по адресу[5] http://twt.mpei.ac.ru/MCS/Worksheets/WSP/PT.xmcd .

Таблицы теплофизических свойств веществ, публикуемые в справочной литературе, как правило, получены в результате расчета по формулам, которые, в свою очередь, получены через статистическую обработку экспериментальных данных с опорой на некие теоретические положения. Если говорить о таком веществе как вода и водяной пар, то соответствующие таблицы термодинамических свойств этого важнейшего теплоносителя и рабочего тела (например, таблица 3) были получены на основе расчетов по соответствующим формуляциям Международной ассоциации по свойствам воды и водяного пара ( www.iapws.org ), в частности по формуляции IAPWS-IF97 (www.iapws.org/relguide/IF97-Rev.pdf). Одним из автором данной статьи была проделана работа по переводу формул формуляции IAPWS-IF97 (набор текстов и «мертвых» формул, оформленных в формате pdf и которые можно «скачать с сайта www.iapws.org/relguide/IF97-Rev.pdf) в «живые» интерактивные сетевые расчеты [6-8] с использованием технологии Mathcad Calculation Server (MCS) [9].

Небольшое отступление от основной темы (интермедия).

Формулы формуляции IAPWS-IF97 охватывают пять областей:

· вода ( http://twt.mpei.ru/MCS/Worksheets/WSP/Region1.xmcd )

· водяной пар (http://twt.mpei.ru/MCS/Worksheets/WSP/Region2.xmcd)

· критическая область (http://twt.mpei.ru/MCS/Worksheets/WSP/Region3.xmcd)

· водяной пар при высоких температурах (http://twt.mpei.ru/MCS/Worksheets/WSP/Region5.xmcd)

· линия насыщения ( http://twt.mpei.ru/MCS/Worksheets/WSP/Region4p.xmcd и http://twt.mpei.ru/MCS/Worksheets/WSP/Region4t.xmcd)

Есть и формуляция IAPWS-IF95 (www.iapws.org/relguide/IAPWS95.pdf), в которой нет разбивки на отдельные область, но вследствие этого расчет ведется по более сложным наборам формул, которые открыты в Интернете по адресу http://twt.mpei.ac.ru/MCS/Worksheets/WSP/iapwsif95.xmcd .

В приведенном выше списке областей формуляции IAPWS-IF97 прописаны адреса соответствующих страниц Интернета, собранных на сайте http://twt.mpei.ru/ochkov/WSPHB. Открытость формул формуляции IAPWS-IF97 позволяет легко их программировать. Данные формулы были реализованы в среде инженерного калькулятора Mathcad и опубликованы в Интернете по уже упоминавшейся технологии MCS. На рис. 1 отображена страница сайта Интернета, зайдя на которую можно выбрать параметры осей X-Y графика (это на рис. 1 не показано) и увидеть конфигурацию данных областей (это на рис. 1 показано для графиков p-T, T-s, Z (коэффициент сжимаемости[6])-ρ и 1/C_p-ρ).

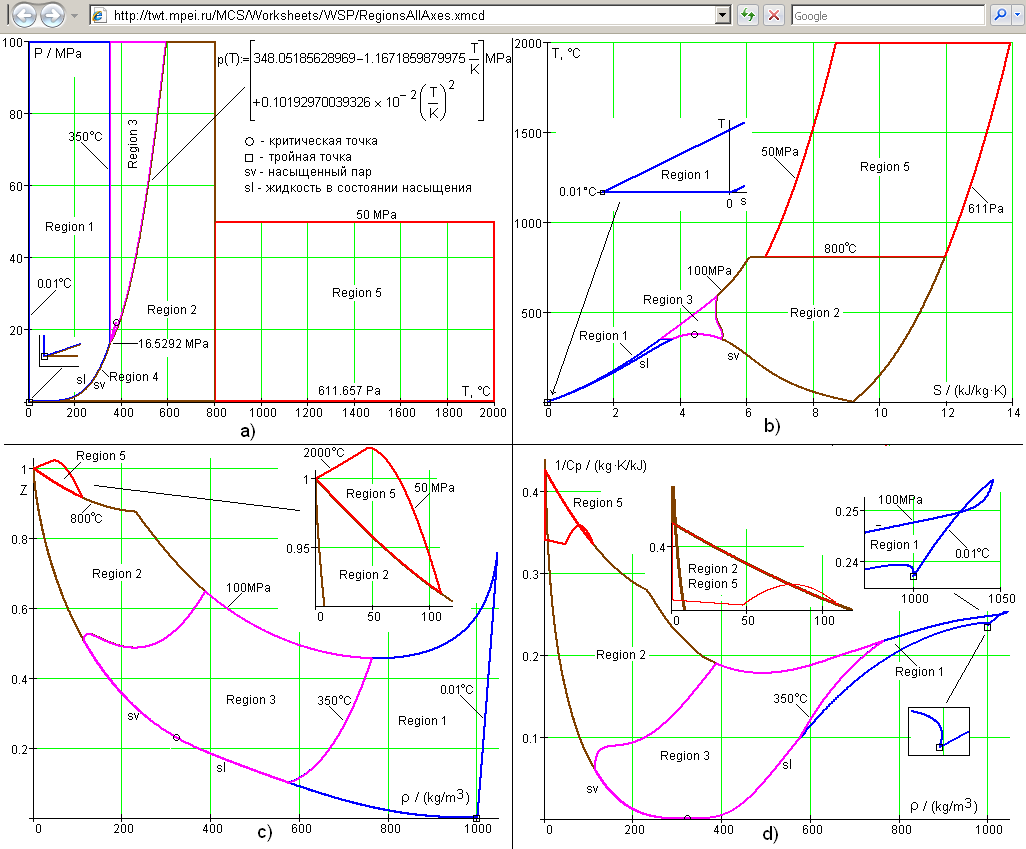
Рис. 1. Конфигурации областей формуляции IAPWS-IF97 в различных диаграммах

В верхнем левом углу рис. 1 (пункт a) показано традиционное «прямоугольное» отображение конфигурации областей формуляции IAPWS-IF97 в рамках p-T диаграммы. В этой диаграмме область 4 сворачивается в одну линию, простирающуюся от тройной точки (273.16 K и 611.657 Pa) до критической точки (647.096 K и 22.064 MPa). В верхнем правом углу рис. 1 (пункт b) конфигурация областей соответствует диаграмме, часто используемой для отображения паротурбинных термодинамических циклов (T-s диаграмма). Две другие конфигурации областей (пункты c и d) используются реже, но они не менее интересны. Диаграмма z-ρ (коэффициент сжимаемости и плотность) показывает, насколько параметры воды и водяного пара отличаются от параметров идеального газа, у которого z = 1. Диаграмма 1/C_p-ρ (величина, обратная значению удельной изобарной теплоемкости, и плотность) примечательна тем, что на ней границы областей образуют некие петли, смысл которых можно уяснить при переходе от плоских к объемным диаграммам [10-11], где выявляется ложность этих пересечений.

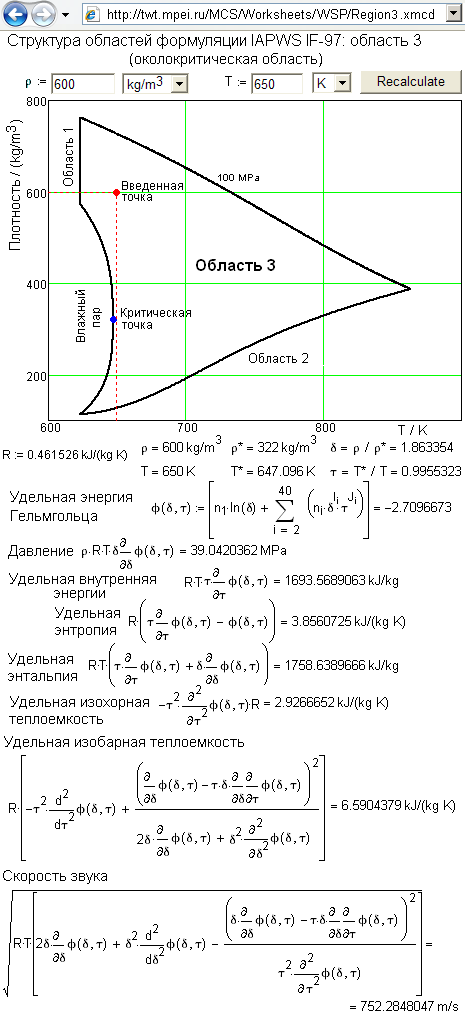
На рис. 2 в качестве примера показана одна из страниц сайта http://twt.mpei.ru/ochkov/WSPHB, где не только дан набор формул, по которым ведется расчет термодинамических свойств воды и водяного пара в околокритической области (область 3 формуляции IAPWS-IF97), но и осуществляется сам расчет с выводом «на печать» всех итоговых и промежуточных результатов.

Рис. 2. Сетевой расчет по формуляции IAPWS-IF97 для области 3 (околокритическая область)

Но вернемся к теме нашей статьи – к расчетам по таблицам, а не по формулам.

Когда в справочной литературе опубликованы формулы для расчета теплофизических свойств веществ, то их несложно запрограммировать и распространять среди пользователей либо в виде пакета программ, если необходимо иметь в собственных прикладных программах соответствующие функции и/или процедуры (см., например, сайт www.wpu.ru, если речь идет о воде, водяном паре, газах и газовых смесях – рабочих телах теплоэнергетики), либо в виде страниц сайтов Интернета (см. выше), если требуются только разовые расчеты. Так (продолжение вышеизложенного отступления), зайдя на страницу Интернета с адресом http://twt.mpei.ru/MCS/Worksheets/WSP/PT.xmcd, можно рассчитать теплофизические свойства воды и водяного пара в зависимости от заданных значений давления и температуры (сетевой аналог табл. 3). При этом значения давления и температуры могут принимать любые значения в рамках, показанных в пункте a на рис. 1, а не дискретные, зафиксированные в «боковике» и «шапке» табл. 3. Более того, зайдя на страницы Интернета с адресами http://twt.mpei.ru/MCS/Worksheets/WSP/PH.xmcd или http://twt.mpei.ru/MCS/Worksheets/WSP/PS.xmcd, можно решить обратные задачи – рассчитать теплофизические свойства воды и водяного пара в зависимости от заданных значений давления и удельной энтальпии или удельной энтропии (окончание отступления).

Но очень часто в справочной литературе информационным ядром являются именно таблицы, а не соответствующие им формулы. Почему!?

Во-первых, нередко никаких формул нет и не было, а в таблицах даны результаты тестирования веществ на предмет определения их теплофизических свойств без особой обработки полученных данных. В таких случаях часто публикуют не таблицы, а графики с кривыми, вблизи которых проставлены экспериментальные точки. На графиках четче видны те или иные зависимости свойств веществ от их параметров (см., например, рис. 1, 9 и 10). Приемы перевода графиков в таблицы изложены в главе 3 монографии [5].

Во-вторых и главных, часто оказывается так, что формулы в справочной литературе имеются и даже в избытке, но воспользоваться ими бывает практически невозможно. Дело в том, что описание формул в некоторых монографиях справочного характера, дано так запутано, что исключается их практическое использование для написания программ не только читателями, но, по-видимому, и самими авторами. Такая «формульная путаница» образуется «вольно или невольно». «Невольно» вероятно потому, что многие книги пишутся урывками разными авторами авторского коллектива в разное время. Такие книги часто не имеют общего научного редактирования, включающего принцип: «Если в книге есть формула, то по ней можно и нужно считать!». В таких книгах часто отсутствуют некоторые коэффициенты формул и читатель должен искать их в других источниках, а также не дано четких ограничений по использованию формул и т.д. «Вольно» путаница в формулах в некоторых особых случаях получается потому, что авторы уже имеют коммерческую программу расчета по описываемым формулам и не хотят плодить конкурентов, но в то же время имеют намерение прорекламировать свои наработки[7].

В любом случае отказ от использования формул и переход к расчетам, основанным на рейперных точках опубликованных таблиц, имеет еще одно важное основание.

Расчет по формулам иногда бывает слишком длительным, что в ряде случаев не удовлетворяет пользователей. Пример – создание компьютерных тренажеров для персонала, обслуживающего теплоэнергетические объекты. Тут не требуется особая точность расчетов теплофизических свойств рабочих тел этих объектов во всем диапазоне рабочих параметров (см. рис. 1), а необходим только быстрый счет в режиме реального времени по программе, работающей в ограниченном диапазоне исходных параметров по несложному алгоритму, например, по линейной интерполяции. Или интерполяции сплайнами, а также аппроксимации – методами, описанными ниже.

В инженерном калькуляторе Mathcad есть встроенные средства решения задач интерполяции и аппроксимации. На рис. 3 показана страница Интернета, на которой по технологии MCS выложен Mathcad-документ с обработкой данных, показанных в табл. 1.

Рис. 3. Сайт Интернета по расчету свойств вещества на линии насыщения

Посетитель сайта указывает нужную ему температуру в отмеченных диапазонах по шкале Цельсия или Кельвина, выбирает из списка нужное ему теплофизическое свойство данного газового конденсата, отмечает нужный способ обработки табличных данных (linterp – линейная интерполяция, spline – интерполяция сплайном, 1-7 – аппроксимация полиномом 1, 2, … 7-й степени), нажимает кнопку Recalculate и получает ответ числом (соответствующая единица измерения отмечена в списке параметров) и графиком с интерполирующей или аппроксимирующей линией, «нанизанной»[8] на нее точками из исходной таблицы. Если же была выбрана аппроксимация полиномом n-й степени, то дополнительно (это на рис. 3 не показано) выдаются значения коэффициентов данного полинома.

Интерполяция сплайнами, которая применяется для обработки данных из табл. 1 (рис. 3), показана ниже на рис. 9 для пары параметров: температура и давление насыщения.

Функцию не одной, а уже двух переменных, с опорой не на два вектора, а на матрицу значений свойств веществ также несложно сгенерировать в среде Mathcad. Стандартные средства этого пакета – встроенные функции вида *spline[9] требуют, чтобы матрица исходных данных (у нас это значения плотности) для уже двумерной[10] сплайн-интерполяции была полностью заполненная и квадратная. При этом значения аргументов (у нас это значения температуры и давления) должны храниться в дополнительной матрице с двумя столбцами. А наша соответствующая матрица не полностью заполнена и не квадратная – см. табл. 2.

Проблему незаполненности матрицы можно решить через дополнительную ее обработку, через вспомогательную интерполяцию – см. рис. 4.

Рис. 4. «Искусственное» заполнение частично заполненной матрицы

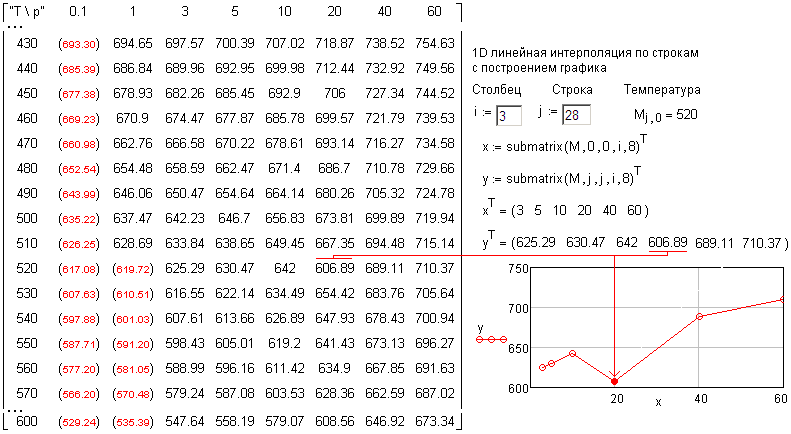
На рис. 4 показано, как с помощью вспомогательной сплайн-интерполяции, вернее, экстраполяции пустые места исходной матрицы (таблицы 2) заполняются некими эрзац-значения, которые не будут затем использованы, но которые помогут нам провести интерполяцию по реальным точкам. Смысл слова «эрзац» тут в том, что мы в этот диапазон в дальнейшем попадать не должны, но эти «эрзац-значения» помогут нам провести интерполяцию у границы фазового перехода. На рис. 4 эти значения отмечены скобками, более мелким шрифтом и иным (красным) цветом[11]. При этой операции заполнения матрицы можно дополнительно вести контроль правильности исходных данных. На рис. 5 показан дополнительный график, фиксирующий аномальный элемент матрицы М_28, 5[12].

Рис. 5. Фиксация ошибки ввода матрицы

Эта аномалия (ошибка, опечатка) является следствием либо неправильного ввода числа при ручном вводе матрицы или при сбое распознавателя текстов при обработке сканированного рисунка матрицы[13], либо могла быть в исходной таблице. Так или иначе эта ошибка (606.89) была исправлена (660.89) – сравните рис. 4 и 5.

После операции ввода эрзац-значений (рис. 4) у нас получается полностью заполненная, но не квадратная матрица. Проблему «квадратности» матрицы можно решить двумя способами:

· вставкой в неквадратную матрицу дополнительных столбцов или строк, элементы которых сгенерированы опять же через интерполяцию;

· сведением одной двухмерной интерполяции к двум одномерным интерполяциям, что мы и сделаем.

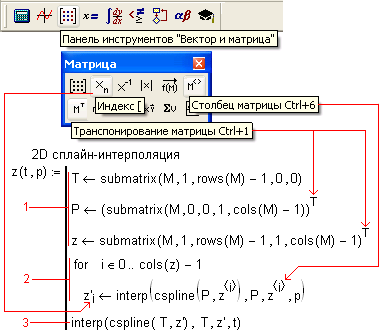
На рис. 6 показано создание функции с именем z с двумя аргументами t и p, реализующей сплайн-интерполяцию данных, хранящихся в матрице М. Для этого:

1) через встроенную в Mathcad функцию submatrix из матрицы М изымаются: вектор Т (дискретные значения температуры – «боковик» таблицы 2), вектор Р (дискретное значение давления – «шапка» таблицы) и матрица z (значение плотности конденсата при соответствующих значениях температуры и давления; подматрица при этом транспонируется);

2) циклом for (циклом с параметром i – номер столбца[14]) с одним оператором в теле генерируется дополнительный вектор z', хранящий значения плотности конденсата в промежуточных точках (первая одномерная сплайн-интерполяция по давлению);

3) по полученным промежуточным точкам (вектор z') стоятся итоговая (вторая) сплайн-интерполяция по температуре.

Рис. 6. Реализация двухмерной интерполяции через две одномерные

Технология двух одномерных интерполяций взамен одной двухмерной имеет то преимущество, что можно в этих двух интерполяциях комбинировать методы, применить, например, в первой интерполяции интерполяцию сплайнами, а во второй линейную интерполяцию. Это позволить в ряде случаев избежать такого «бича» интерполяции как осцилляции (колебаниям) между узлами сетки интерполяции. Кроме того, такое разделение дает возможность более широко комбинировать методы обработки табличных данных, применять, например, по одному аргументу интерполяцию, а по другому – аппроксимацию[15].

При выводе ответа «на печать» с помощью функции if (рис. 7) отсекаются ответы, исходные данные для которых выходят за рамки допустимых.

Рис. 7. Операторы, подготовки ответа к выводу «на печать»

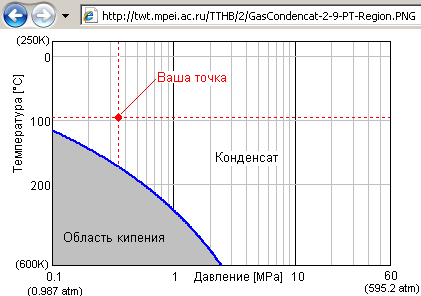
При формировании ответа (см. рис. 7) учитываются не только прямоугольные границы таблицы значений плотности (табл. 2: 250-600 K по температуре и 0.1-60 MPa по давлению), но и линия начала кипения – см. рис. 8, который также размещен в Интернете и на который есть соответствующая ссылка из области задания исходных значений температуры и давления (см. рис. 8). Если исходные данные выходят за рамки допустимых, то переменным, выводимым «на печать», присваивается не численное значение, значение специальной переменной NaN (Not a Number – не число). Но эти ограничения нужно будет снять, если функция z(t, p), будет использоваться для решения обратной задачи, для численного определения, например, температуры по давлению и плотности или давления, по температуре и плотности. В этом случае при реализации итераций допустимо выходить за рамки значений температуры и давления, очерченных на рис. 8. Тут, правда, линейная интерполяция не будет годиться, т.к. производная от данной функции является константой. Сплай-итерполяция тем и хороша, что соответствующие функции имеют первую и втору производные, что часто бывает необходимо при реализации различных численных методов: метода Ньютона поиска корней или метода градиентного спуска при поиске минимума.

В расчете используются невидимые переменные (это допустимо в среде Mathcad: переменные с белым цветом шрифта на белом фоне), что упрощает чтение итогового документа (см. рис. 10 ниже). Переменные-диапазоны с именами tt и pp будут являться аргументами при построении графиков.

Рис. 8. Область допустимых значений температуры и давления для интерполяционной функции

На графике, показанном на рис. 8, как заметил читатель, шкала абсцисс перевернута: низкие температуры находятся вверху, а высокие внизу. Это сделано намерено для того, чтобы визуально приблизить данный график к соответствующей ему таблице 2. Так сложилось исторически, что в «боковиках» таблиц числовые значения (значения температуры, если иметь ввиду табл. 1, 2 и 3) почти всегда увеличиваются сверху вниз, а на осях ординат графиков – снизу вверх. На рис. 8 эта традиция нарушена.

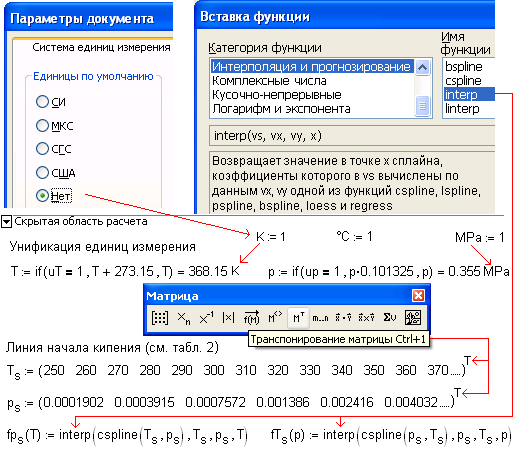
На рис. 7 было показано окончание свернутой области, а на рис. 9 ее начало[16].

Рис. 9. Начало свернутой области расчета плотности газового конденсата

На рис. 9 показаны, операторы, во-первых, учитывающие разные единицы измерения[17] при вводе исходных данных, и во-вторых, осуществляющие через одномерную сплайн-интерполяцию формирование двух функций пользователя: функцию fp_s(T) и fT_s(p) – прямую и обратную функцию зависимости давления и температуры начала кипения, которые будут использованы (см. рис. 7) для контроля нахождения исходных данных в оговоренном диапазоне (см. рис. 8).

После всех вышеперечисленных действий получена и опубликована в Интернете страница, показанная на рис. 10.

Рис. 10. Страница Интернета с интерактивным расчетом плотности газового конденсата

На странице Интернета, показанной на рис. 10, есть ссылка на сервер, с которого можно скачать соответствующую функцию, возвращающую плотность газового конденсата. Эту функцию можно вставить в собственный Mathcad-расчет и работать автономно без выхода в Интернет. Соответствующие функции можно создать и с использованием традиционных языков программирования (BASIC, Pascal, C и др.), имея под рукой открытый код расчета. Это еще одна причина, почему в нашем расчете не был задействован в полной мере инструментарий физических величин и единиц их измерения, встроенный в пакет Mathcad [12] – в «традиционных языках программирования» этих средств нет.

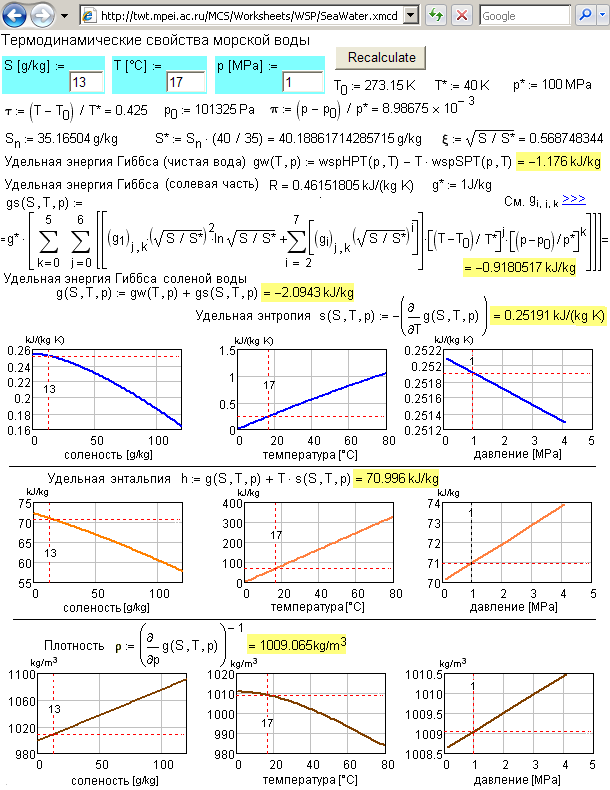
На рис. 10, показано, что не только выводится рассчитанное числовое значение плотности газового конденсата в зависимости от заданных значений температуры и давления, но показаны также изобара и изотерма, что позволяет прогнозировать изменение данного свойства при изменении внешних условий. Функцию двух аргументов можно было также отобразить и поверхностью, а не только двумя изолиниями (изобара и изотерма), но мы этого не делаем по двум причинам. Во-первых, при публикации Mathcad-документов в Интернете по технологии MCS, как правило, нельзя менять ориентацию поверхности в виртуальном пространстве экрана дисплея для нахождения лучшего ракурса. И во-вторых, теплофизические свойства веществ, а в особенности смесей веществ[18], зависят не от двух, а от трех и более параметров, и их уже нельзя отобразить графически поверхностью. Тут можно использовать только изолинии. Рис. 11 иллюстрирует этот тезис.

Рис. 11. Страница Интернета с интерактивным и открытым расчетом теплофизических свойств морской воды

Заключение:

При выполнении инновационной образовательной программы (http://inedu.mpei.ru), проводимой Московским энергетическим институтом (www.mpei.ru) в рамках решения проблемы передачи знаний от поколения к поколению [13] и развития Электронной энциклопедии энергетики (www.trie.ru), были созданы страницы Интернета, на которых ведется расчет теплофизических параметров более чем 3000 веществ, смесей веществ, металлов, сплавов и других материалов, применяемых в энергетике в качестве рабочих тел, теплоносителей, конструкционных материалов и т.д. Доступ к этим станицам открыт через Интернет-версию пятого тома [5] справочной серии «Теплоэнергетика и теплотехника» [14]. Адрес http://twt.mpei.ru/TTHB .

Литература[19]:

1. Григорьев Б.А. Теплофизические свойства и фазовые равновесия газовых конденсатов и их фракций / Б.А. Григорьев, А.А. Герасимов, Г.А. Ланчаков; под общ. ред. Б.А. Григорьева. – Издательский Дом МЭИ, 2007

2. Александров А.А., Григорьев Б.А. Таблицы термодинамических свойств воды и водяного пара. – М.: Изд. МЭИ, 1999

3. Очков В.Ф. Теплотехнический справочник в Интернете // Новое в российской электроэнергетике, № 5, 2005

4. Очков В.Ф. Математические пакеты и сетевой интерактивный теплотехнический справочник: проблемы и решения // Теплоэнергетика, № 6, 2006

5. Очков В.Ф. Интернет-версия справочника Теплоэнергетика и теплотехника. Инструментальные средства создания и развития / Г.Ю. Кондакова, А.С. Копылов, К.А. Орлов и др. – Издательский Дом МЭИ, 2007 (издание выпущено при финансовой поддержке Российского фонда фундаментальных исследований www.rffi.ru)

6. Александров А.А. Теплофизические свойства воды и водяного пара в Интернете / А.А. Александров, В.Ф. Очков, К.А. Орлов и др. // Промышленная энергетика № 2, 2007

7. Очков В.Ф. Свойства теплоносителей и рабочих тел энергетики: информация в Интернете / А.А. Александров, В.Ф. Очков, К.А. Орлов и др. // Новое в российской электроэнергетике. №1, 2008

8. Alexandrov А.А., Ochkov V.F., Orlov K.A. Steam Tables and Diagrams on Mathcad Calculation Server for Personal Computers, Pocket Computers and Smart Phones // Proceedings of the 15th International Conference of the Property of Water and Steam, Berlin/Germany, September 7–11, 2008

9. Очков В.Ф. Mathcad 14 для студентов и инженеров: русская официальная версия. С-Пб.: БХВ-Петербург, 2009

10. Очков В.Ф. Сетевые расчеты и диаграммы теплоэнергетических процессов // Промышленная энергетика № 12, 2008

11. Очков В.Ф. Интернет-расчеты термодинамических циклов / В.Ф. Очков, А.А. Александров, В.А. Волощук и др. // Теплоэнергетика, № 1, 2009

12. Очков В.Ф. Физические и экономические величины в Mathcad и Maple. М.: Финансы и статистика, 2002

13. Очков В.Ф., Яньков А.Г. Математические пакеты и проблема передачи знаний // Пленарный доклад на VI школе-семинаре молодых ученых и специалистов академика РАН В.Е.Алимасова «Проблемы тепломассообмена и гидродинамики в энергомашиностроении», 16-18 сентября 2008 г. Казань, Россия

14. Теоретические основы теплотехники. Теплотехнический эксперимент: Справочник / Под общей ред. А.В. Клименко и В.М. Зорина. 3-е изд., перераб. и доп. М.: Изд-во МЭИ, 2001

---

[1] Или давление начала кипения, если говорить о смеси веществ как в нашем случае с газовым конденсатом

[2] Концепция «облачных» вычислений подразумевает предоставление удаленных вычислительных мощностей, дискового пространства и каналов связи заказчику, когда прикладные программы запускаются не на собственном компьютере (на рабочей станции), а на удаленном сервере (в «облаках»), обслуживающем отдельную локальную сеть или весь Интернет. Компании, университеты научные и проектные организации подталкивает на переход к «облачным» вычислениям высокая стоимость обустройства и обслуживания собственных локальных сетей и серверов, стремление к экономии электроэнергии и средств на покупку лицензионного программного обеспечения, низкая стоимость сетевых переносных рабочих станций (NetBooks) и другие факторы, формирующие современный вектор развития IT-технологий

[3] Смысл слова «мертвый» будет раскрыт ниже

[4] Табл. 3 высвечивает нам одну проблему, напрямую связанную с темой статьи. В таблице десятичным разделителем в числах является запятая, а на сайте – точка. В настоящее время все страны постепенно переходят к единому стандарту – к точке. Но в России и некоторых странах СНГ по-прежнему тут используется запятая, что вызывает ряд проблем, т.к. стандартом для большинства программных сред является точка. Эта проблема давно бы была решена и Россия, следуя тенденциям глобализации, перешла бы на мировой стандарт, если б не популярный табличный процессор Excel, в среде которого можно работать как с точкой так и с запятой в качестве десятичного разделителя. Еще одна дань глобализации – использование на описываемых расчетных сайтах Интернета латинских, а не русских написаний единиц измерения. Это наряду с возможностью смены языка комментариев расширяет круг посетителей сайта.

[5] Данную страницу можно найти и через поисковые машины Интернета, введя в текстовое окно «поисковика» (оно показано внизу табл. 3 – см. слово Google) соответствующие ключевые слова «свойства воды и водяного пара», например.

[6] z = p · v/ R · T

[7] Тут возможны следующие «шпионские» действия. По такого рода закрытой программе формируются таблицы, подобные табл. 1 и табл. 2. Затем по полученным таблицам воссоздается программа с использованием, например, приемов описанных в данной статье

[8] «Нанизанными» в случае интерполяции, когда кривая проходит строго через табличные точки. При аппроксимации кривая проходит вблизи табличных точек, выполняя критерий «наименьших квадратов». Тут возможны и другие аппроксимирующие зависимости помимо использованного полинома n-й степени. При этом аппроксимацию возможно вести не во всем заданном температурном диапазоне, а в ограниченном, нужном конкретному пользователю

[9] Тут на месте звездочки могут стоять буквы l (эль), p или с (см. рис. 9), отмечающие линейное (l), параболическое (р) или кубическое (с) продолжение интерполяции (экстраполяцию) за пределы диапазона заданных точек

[10] На рис. 9 была показана одномерная сплайн-интерполяция, через которую можно сгенерировать функцию одного аргумента

[11] Цвет виден, естественно, только на цветных рисунках. Для черно-белых рисунков были дополнительно задействованы скобки и мелкий шрифт

[12] Пересечение 28-й стоки (j) и 5-го столбца (i) матрицы M. Значения целочисленных переменных j и i можно менять (см. рис. 4 и 5), выбирая тем самым

[13] В настоящее время в Интернете стали размещаться подобные матрицы, которые просто можно копировать в программные среды для работы с ними. Тут, правда, остаются уже не технические проблемы (сканирование и распознавание текста), а юридические, касающиеся авторских прав. Первый шаг в решении этой проблемы – это указание на источник данных, что мы, естественно, делаем в этой статье

[14] В среде Mathcad по умолчанию нумерация строк и столбцов матриц и векторов начинается с нуля

[15] Вопрос о точности методов интерполяции и аппроксимации остается за рамками данной статьи и требует отдельного исследования. Этот вопрос усложняется и тем, что в справочной литературе, откуда берутся таблицы для их обработки методами, описанными в статье, очень часто не ничего не говориться от точности значений свойств веществ, сведенных в таблицы. Пример расчета теплофизических свойств вещества с указанием погрешности можно видеть на сайте http://twt.mpei.ac.ru/MCS/Worksheets/WSP/Region4t.xmcd

[16] Надо было бы наоборот, но так уж получилось при описании расчетного документа. Надеемся, что читатель поймет эту логику и простит автора

[17] Пакет Mathcad оборудован средствами работы с физическими величинами и единицами их измерения [11]. Но в нашем расчете эти средства были отключены: единицы измерения (MPa, kg, m, K и °C) использовались только в качестве комментариев в конце числовых значений. Это вызвано тем, что инструментарий единиц измерения в среде Mathcad не полностью состыкован с функциями интерполяции и аппроксимации. И это понятно. Единицы измерения связаны с физической (сущностной) стороной явлений, а функции интерполяции и аппроксимации с описательной (феноменологической)

[18] Тот же газовый конденсат, как можно предположить, меняет свой состав и, следовательно, теплофизические свойства во времени, по мере разработки месторождения

[19] Литература, где одним из авторов является В.Ф.Очков, открыта на сайтах http://twt.mpei.ru/ochkov/work1.htm  и http://twt.mpei.ru/ochkov/work2.htm. Там же можно найти расширенный вариант данной статьи.