Thermodynamic cycles: calculations on the Internet
Proceedings of the 7-th Conference «Power System Engineering, Thermodynamics & Fluid Flow», June 26-27, 2008, Pilsen, Czech Republic, pp. 165-173
V.F. Ochkov
New approaches
of thermodynamic cycle calculation are described using modern network
information technologies that can change calculation methods and instruction
principles in heat engineering
Today
mathematical packages are used widely in education and engineering practice
that demand revision of calculation techniques and new instruction methods.
The main base of
calculations in various scientific disciplines (in particular, thermodynamics)
is a set of formulae and algorithms, that was formed for hand computation in
pre-computer (and even in pre-calculator) era. This puts a kind of seal on
formulae and methods of their application that impedes their use in computer
calculations and to understanding of a scientific discipline by students. The
formulae were often excessively simplified. Moreover, some approaches were
omitted in lots of formulae related with so named “technology” reasons, i.e.,
with methods and technical means of calculations used in times of formula
deducing that don’t connect with its physical essence.
There is a
classical example from thermodynamics. Fig. 1 shows an Internet site where with
calculation of the thermal efficiency of a thermodynamic Otto cycle formed by
two isochoric and two isentropic processes.
A few people remember how this formula was developed and that it is
correct if cp and cv
(specific isobaric and isochoric heat capacities of working medium) are related
with temperature. It is an ideal case which does not correspond even to a gas
with constant composition. In reality, working substances for power plants are
mixtures with changing composition – fuel-air mixtures, combustion products,
etc.
Figure
1. Calculation of
thermal efficiency of thermodynamic Otto cycle by a simplified formula
(http://twt.mpei.ru/MCS/Worksheets/Thermal/Otto-cycle-1e.xmcd)
Returning to the
thesis noted in the beginning of the article, and connecting it to
thermodynamic cycle calculations, it is possible to regenerate the initial
formula (more precisely, a set of formulae and algorithms). Modern mathematical
systems (Mathcad, in particular) can give us not only Otto cycle efficiency but
all intermediate values –parameters of working medium at various points of the
cycle. Fig. 2 shows this calculation.
Figure
2. Calculation of
Otto cycle thermal efficiency by initial formulae
(http://twt.mpei.ru/MCS/Worksheets/Thermal/Otto-cycle-2e.xmcd)
Fig. 2 shows
that for an Otto cycle calculation in Mathcad, a built-in operator was
used. This was a definite integral type
and the block (Given-Find) for system solving, in this case, for a system of
integral-algebraic equations. These tools allow us to compute the main relations
of thermodynamics: Mendeleev-Clapeyron equation PV
=RT, integral over temperature and pressure for calculations of entropy S,
enthalpy H, and integral over temperature for calculations of internal energy
U. These provide the possibility to find the values of internal energy U at all
four points of an Otto cycle and to calculate the cycle
efficiency using these values. Fig. 2 shows that the constants cp and cv are not taken out of integrals.
For more complicated (real) calculations we can substitute appropriate
functions of one (temperature), two (temperature and pressure) or more
(temperature, pressure, composition of gas mixture) variables for these
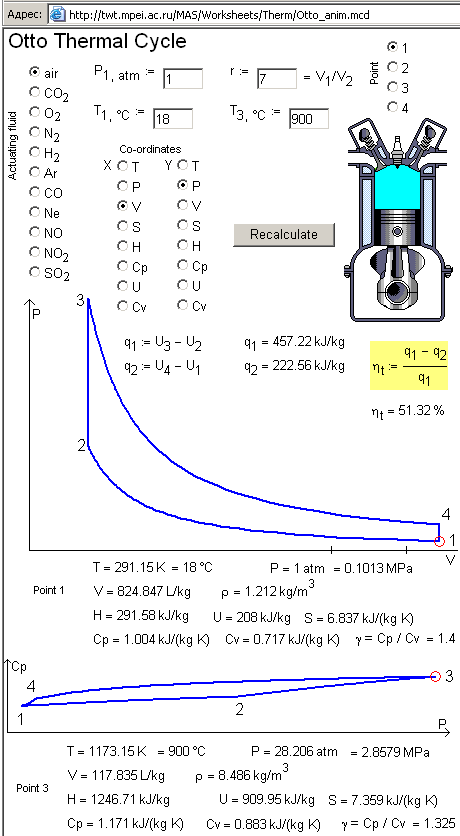
constants. Fig. 3 shows the calculation where a user can choose the
working medium, its parameters (pressure p1, temperature T1, the volumetric
compression ratio r, maximal temperature T3), and specify the axes of the
diagram visualizing the cycle, or a point in the cycle of internal-combustion
power plant.
Figure
3. Calculation of
Otto cycle where specific heat of working medium depends on temperature
(http://twt.mpei.ac.ru/MAS/Worksheets/Therm/Otto_anim.mcd)
Fig. 3 shows two
diagrams in the end of an Otto cycle calculation. One of them is the usual p,V-diagram (this and other
diagrams are possible to plot by choosing proper buttons on the axes). Another is a cp,p-diagram which represents the dependence of
specific isobaric heat capacity of the working medium (air, on Fig. 3) on
temperature within limits of its changing in the Otto cycle. In this calculation
a user can choose a point of the cycle: first point is the beginning of
compression process, point 2 is the end of compression, point 3 is the end of
isochoric combustion of fuel-air mixture (here the heat capacity values depend
on temperature and on composition of the working substance), and the last point
4 is the end of piston stroke. The chosen phase determines the current shot of
animation, the outlined point on the diagram, and represented working substance
parameters.
In the network
document shown on Fig. 3 the calculations of the working substance parameters
are carried out not only for four points as it shown on Fig. 2 but also for
intermediate points with a given step. These allow us to create vectors which
elements are parameters of the working substance (p, T, v, s, h, U, cp, and cv) and also to plot volumetric
graphs in various systems of coordinates (for example, see Fig. 6 below).
There is a
second difference between the calculations presented on Fig. 2 and Fig. 3.
Fig. 3 shows calculations based on functions provided by the WaterSteamPro™ package
(www.wsp.ru) without using relations for ideal gas. For example, cp =aR where a is a constant related
with gas composition.
The
WaterSteamPro™ package has been created as a tool for users to calculate
heat-transfer properties of water and steam in program languages C, Fortran, BASIC, Pascal, tabular processor Excel, and
mathematical packs such as Mathcad, MatLab, et
cetera. Additionally, the list of functions with prefix wsp
was increased and the functions with prefix wspg were
added for calculations of thermodynamic properties of individual gases and gas mixtures.These enable us to apply the WaterSteamPro™
package for calculating steam power, gas turbine and also combined-cycle
plants. The functions of the WaterSteamPro package are accessible for use on
the Internet. Fig. 4 shows the Internet site in which a user can introduce
values in text boxes, press the Recalculate button and obtain
numerical results –the values of entropy, enthalpy and other properties of the
working medium.
Figure
4. Calculation of
parameters of the working media in power engineering
Mathcad
Calculation Server technology, supplemented with the author’s technology of
access to a broadened list of built-in functions of numerical and symbolic
mathematics of Mathcad and Maple packages, allows us to change educational
sites concerned with the theoretical principles of heat engineering.
Let us return to
Figures.1 –3 and try to change the problem statement solved on these sites. Figures. 1 –3 show that a user can change input data, send
it to the calculation server (Mathcad Calculation Server), press the
Recalculate button and obtain new results as numerical data, graphs, and
pictures. Mathcad Calculation Server technology also gives us the possibility
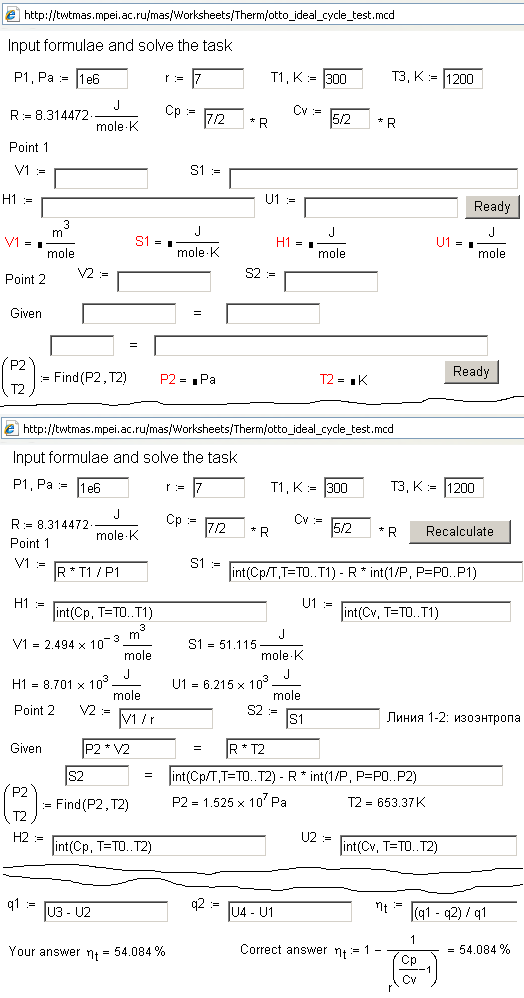
to create sites for distributing knowledge such as for distance education. Fig.
5 shows the site (upper part) where a visitor (for example, a student solving
thermodynamic problem in time of examination) must input the formulae for the correct calculation of the thermal efficiency of
an Otto cycle and other parameters. If the formulae were input correctly (int is integral, diff is differential and other – here it
is used as notations and built-in functions of mathematical packs Mathcad and
Maple which have now become a standard “man-computer” interface) then value in
fields “Your answer” and “Correct answer” (see the bottom part of Fig. 5) must
coincide.
Figure
5. Network
template and correctly filled network template of a thermodynamics problem
The main feature
of the text task presented on Fig. 5 and Fig. 6 is that a student
should work with formulae but not with numbers. A lot of test systems demand
some formula evaluations without entering the formula itself. As a result, it
is often impossible to determine where the mistakes were done: in calculations
or in selection of formulae.
The author’s
method of network testing including analytic transformation and numerical
calculations enables a student to give various answers. For example, the
variants may be R*int(1/p, p=p0…p1) or R*(p/p0) or R*ln(p)
–R*ln(p0). By the way, the last two expressions are
not adequate if variables p and p0 have dimension of pressure. This is a result
of the reasons mentioned in the beginning of this paper: an attempt to simplify
calculations and substitute subtraction for division.
There is another
form of Internet education for heat-and-power engineers, as mentioned before:
demonstrated through three-dimensional graphics.
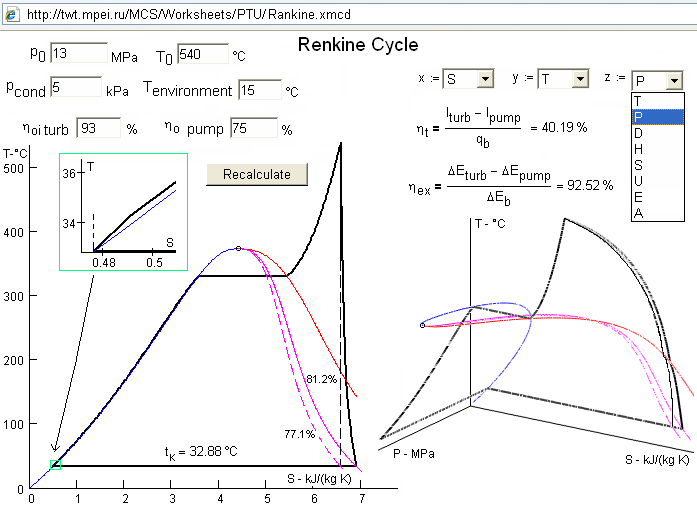
Figure
6.
Three-dimensional graphics of Rankine cycle
For example,
Fig. 6 shows diagrams built on the base of WaterSteamPro™ functions for a Rankine cycle.
We can make
network calculations both for scalar values and for vectors i.e. with a number
of elements of initial data using “vectorization” of
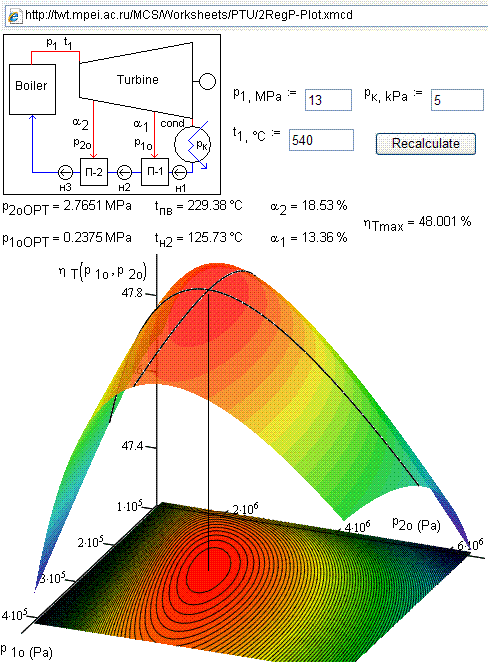
calculations. Fig. 7 shows such a calculation and the optimization of a steam
plant with two reheats.
Figure
7. Calculation and
optimization of steam unit cycle with two reheats
Using the
Internet sites we can carry out the calculations of cycle efficiency quickly
and clearly. Different gases can be introduced as the working medium. For
example, we can determine that for all the gasses (with the exception of
monatomic), thermal efficiency of the Otto cycle depends
on the volumetric compression ratio and also on the maximum temperature of gas.
Thus, the difference between the cycle thermal efficiency and those values
calculated by the simplified formula may amount to 5% or more. Obviously, that
inaccuracy is intolerable in engineering calculations and students must be
trained to avoid the application of simplified formula. It is especially
important to take into account the dependence of cycle efficiency on parameters
of the working medium in optimized calculations.
Changing
simplified formulae to base algorithms of calculations (it may be called
calculation Renaissance) enables us to return from ideal processes to real.
Other
calculations of thermodynamic cycles accessible on the Internet (http://twt.mpei.ac.ru/TTHB/2/ThermCycleMCS.html):
discussed above for their improvement.
References:
1. V.F. Ochkov. Mathcad Application Server:
The experience of exploitation in Russia // SoftLine
Direct.2006, No 11,P.96 –98
2. V.F. Ochkov. Mathcad 14 for students and
engineers // SPb: BHV-Petersburg, 2007
3. A.A. Alexandrov. Thermodynamic principles
of power plant cycles // M.: Publishing House of MEI, 2004, 158 pp.
4. A.A. Alexandrov, K.A. Orlov, V.F. Ochkov.
Mathematical packages – new approach of calculations in thermodynamics and
other scientific disciplines // Izv. vys. ucheb. zav.
Problems of energetics.
2005, No 11-12, P.80-86
5. A.A. Alexandrov, V.F. Ochkov, K.A. Orlov.
Equations and programs for calculations of properties of gases and combustion
products //Thermal Engineering, 2005, Vol. 52, No 3, P. 28-37
6. A.A. Alexandrov, K.A. Orlov, V.F. Ochkov.
Investigation of schemes of steam-gas plants with injection of steam in gas
flow on base of elaborated applied programs for properties of working
substances of PGU //New in Russian electroenergetics,
2004, No 4, P.28-37
7. V.F. Ochkov. Mathematical packages and
network interactive reference book: problems and solutions // Thermal
engineering, 2006, Vol. 53, No 6, P.71-77