Formulae[1] in scientific publications: problems and solutions
The
author with colleagues has prepared a reference book for publication. The
reference book on thermal and physical properties of heat carriers and working
media in power engineering has been supplemented with the Internet site at
http://twt.mpei.ac.ru/rbtpp which contains interactive open calculations [2-7]
described in the “paper” reference book[2].
This article describes some problems and disagreements arisen while preparing
the copy for publication and the ways to tackle them.
Recently the formulae in scientific and technical publications are more often presented as parts of calculations created with the mathematical packages (Mathcad, Maple, Mathematica, MatLab, etc.) rather than rows of symbols entered manually[3] or by means of special programs (Word Equation, LaTex, etc.). Moreover, listed mathematical packages have their own tools to comment on a calculation and format texts-marginalia that enables us to prepare manuscripts[4] for publication without help of special programs (Word, Adobe Acrobat, etc.).
The most popular is a compromise technology. An author passes a plain text in a doc-file to a publishing house or editorial staff, which contains only formatted text and raster figures, for example, as bmp-files.
In addition to the usual figures (schemes, photos, diagrams, plots) bmp-files sometimes contain formulae as screenshots[5] of problems, solved in the mathematical packages.
The fact that formulae are inserted by using the service of an intermediary, the mathematical programs, rather than typing directly is explained by the following reasons. One of them is that manual typing of the formulae (without testing them in the mathematical packages) may result in mistakes (misprints) made by the author and missed by editors and proofreaders while working at a manuscript or a layout of a book or an article. But the main reason is that recently processing of experimental data is done with mathematical packages as well as processing of different tables, plots or estimation of theoretical inserts with representing final and intermediate results. It is desirable to transmit all these manipulations into the book or the article without changes or misrepresentations. There are some other reasons of mathematical package expansion into scientific publications that are discussed below.
Here some problems have arisen which demand solutions.
1. Decimal separator
Traditionally a comma is used as a decimal separator in Russia. But in the other countries (generally in the English-speaking countries) a point is used. Today the USA sets the tone for information technologies, so all basic programs use point as a decimal separator, even if they are created in Russia[6]. Due to this, the text in books and articles inserted from a mathematical package contain points. At the same time, the numbers from the text describing the formulae contain commas. According to the rules, editors and proofreaders[7], who guard standards, forbid the author to put points in the numbers. Sometimes it is difficult to prove that we cannot substitute commas for points in the “computer” formulae. Otherwise, if a reader decides to copy such a formula[8] from the book into a program he would be faced with an error.
At the present time many countries that traditionally have used commas in numbers (for example, Germany[9]) are gradually changing to points. Recently a German colleague gave the author his new book and asked him to let him know if there would be a comma in the numbers. It is necessary to draw a line under the point problem. Some of the publishing houses in Russia completely switched for points already. Here one can note something like Fronde aimed against the stiff rule, which isolates the country from “printing mainstream”.
While perestroika of eighties-nineties of the last century, one of our revolutions, radical westerners believed that Cyrillic should be urgently substituted with Latin[10]. Some of the newspapers and magazines ostentatiously used Roman instead of Cyrillic[11] for printing. At that, they emphasized that Latin would help us to be acquainted with western values, to accelerate computerization process and so on.
One can imagine if life were to make us substitute commas for points some people and publications would ostentatiously place commas as those Paris boys who continued playing fronda (a game with sling) after it was banned by police due to numerous injuries[12].
The problem of point and comma is complicated by international financial format of numbers (###,###,###,###.##) in which a comma is a thousandth symbol and point separates dollars/Euros from cents. As a rule, engineering and scientific calculations do not require such accuracy and numbers are rounded even in technical and economic assessments, which contain physical quantities (mass, energy, time) and financial ones.
2. Names of variables used in formulae
The variable names can contain Latin, Cyrillic, and Greek[13] letters. There are a row of values (constants and variables) that has been held traditionally fixed letter combination long before computer appearance. As a rule, the lists of such variables are placed in the beginning of a book. Viewing his “native” formula a specialist can understand what a certain variable holds. At that, the variables can have their “nationality” and “internationality”. Compare Din and Dâõ, Dout and Dâûõ (inlet and outlet diameter of something). These variables contain Latin and Cyrillic letters. Although recently, Cyrillic letters are often rejected in the formulae for practical (not political) reasons.
As we noted above, the formulae for articles and monographs are created oftener in mathematical applications. Some of programs have restrictions on using Cyrillic and even Greek letters, widespread in “international” formulae, in the variable names.
Pure English variables in formulae significantly simplify scientific exchange. A professional who does not know Russian can find a specialized Russian article on the Internet by the English abstract and view its “English” formulae. Understanding their meaning he can order a translation or get into touch with an author. For the same reason the units of physical quantities in this article are international.
Speaking of variable names it is necessary to refer to “variables-hieroglyphs”. A reader may think the matter is China, Japan, Korea and other Asian countries[14] those scientists insert hieroglyphs into the variable names[15]. But what is at issue that some variable names in some branches “are covered with” superscripts, subscripts, character strokes and other specific symbols and look like hieroglyphs now rather than abbreviation. These hieroglyphs are easy to write on a piece of paper or on a blackboard. Having skills one can insert them into a file by means of Word Equation or LaTex[16], although it can be absolutely impossible to insert them in a mathematical application. Such composite names should be simplified: deprived of multistoried form, transformed into the text form. Approximately in this way the Chinese, the Japanese, the Korean have to simplify their scripts to feed data into the computer. For this reason compound names in many disciplines have got their simplified analogues. Symbol of the definite integral could be entered as a picture[17], by a character set, or typing int(f(x), x = 0..1).
As was noted above, many authors place lists of variables in the beginning books and articles. The variables are often presented in a table: the first column contains the name of the variable, the second —its dimension (about dimensions see section 5), and the third contains its description. If a book or an article contains fragments of a program or records of a problem solution in a mathematical application the table is completed with the column containing identifier of the variable used in a computer solution of the problem. Sometimes this column substitutes the first one, containing traditional names of variables and constants. With an expansion of the mathematical packages into the books and articles such a substitution will be more intensive and we will have to forget traditional “hieroglyphic” notation of variables and even some operators (see section 7 below). On the other hand, creating new versions developers of the mathematical packages try to take into account traditions of the variable notations and introduce new tools for their formatting. Thus, Mathcad enables us to include superscripts and subscripts, mathematical symbols. Although, such complicated variables should be put in brackets: [HCO3-], [Dinmin], etc.
3. The order in formula publication
The formulae in books and articles are published in such an order: first the formula itself with a title, for example:
“Thermodynamic temperature of the ideal gas is calculated by formula:
![]() (1)[18]”
(1)[18]”
After that it is listed variables occurring in the formula:
“Where:
m —molar mass, p — gas pressure, v — specific volume and R — universal molar gas constant.”
To make the formula work in the mathematical package it is necessary to change the positions of the formula and the list of its variables and previously enter numerical values[19]: see Fig. 1— screenshot of the problem solution in Mathcad.
|
|
( 2[20] ) |
Figure 1. Calculation by the formula in Mathcad.
It might appear excessive to display numerical values with the formula. However, we should pay attention to the following important tendency of processing technology.
The calculations created in Mathcad and in the other mathematical programs could be published on the Internet for interactive work. Figure 2 shows the webpage with address http://twt.mpei.ac.ru/MCS/Worksheets/pv-RT.xmcd[21]. A viewer can change initial data in boxes, click the button labeled Recalculate and get a new result — temperature calculated by the formula (1).
|
|
( 3[22] ) |
Figure 2. The Online calculation
“Aerial acrobatics” in the formula publication, especially in the electronic edition, is to place link to the site near the formulae where the formulae should work: if one changes initial data he gets a new result.
The author works in a research team from the International Association for the Properties of Water and[23] Steam (www.iapws.org). This association prepares and publishes formulations used to calculate various parameters of the important natural substance. Usually the formulations are published as PDF-text which contains “dead” formulae. Figure 3 shows a part of the formulation for calculation of the ionic product of water, product of concentration of H+-cations and OH--anions in water.

Figure 3. A formulation of properties of water
Recently at the suggestion of the author and his colleagues [4] the formulations have been published as a set of “living” Internet formulae. A viewer can use them for calculation. Figure 4 shows the network document that enables us to calculate the ionic product of water Kw, or rather negative common logarithm of this value pKw depending on temperature and density of water.

Figure 4. A “living” Internet formulation for properties of water and steam.
The formulations for properties of water and steam are developed, confirmed and published also on the Internet to create programs for computation, which need industries, research, design, educational institutes. Tables and plots discussed below are suitable for manual calculations or raw estimation. Publication of the formulations on the Internet in the form of online calculations enables us:
1. To get acquainted with a calculation method (probably, it is better to study traditional PDF-documents).
2. To make one-time calculations: change the initial data and get a new result.
3. To create easily and to check out quickly corresponding programs having not only aggregate results (as a rule, “dead” formulations contain check results for several points, too) but also all intermediate data. Figure 4 shows all formulae of this “live” formulation are supplemented with numerical values.
In the beginning of the article it was announced book [1]. So, all the formulae of this book have their “network-interactive-open”[24] analogues. They were developed by the technology shown on pairs of Figures 1-2 and 3-4.
Authors of the other similar books enclose disks with programs to calculate by formulae from the books. But this technology is obsolete if we take into consideration that almost all computers today are provided with the internet access. Although, downloading instead of program setup from the disk enclosed could not solve the problem completely.
It should be noted that the following tendency will change users’ lives in the near future: cloud computing, providing with remote computational power, disk space, and link channel. Apart from everything else, users have to utilize cloud computing due to high costs of license for standalone computers, leasing of premises, power, software piracy countermeasures, and the trends described in this article. There will be no need for a user to install applications in his personal computer as he will find everything on the Internet at a moderate charge or free of cost.
There is additional advantage in location of calculation programs on the dedicated server instead of distribution of disks enclosed to the books. If one find an error in the program or just a misprint in the comments it can be corrected quickly and by insensible degress. Such server can also contain continuously complimented list of misprints from the book itself (this experience is being spread currently). The book that has numerous spider lines of the references into a server can be considered as continuously “reprocessed, supplemented, improved” publication.
Different problem books and work-books[25] contain plenty of formulae. The author with the students used to transfer some of them, connected with power engineering, into the “network-interactive-open” format. If only you know how many errors and misprints were found there! These are not only traditional errors (a squared variable instead of that rose to the third power) but also non-disclosures/omissions which a specialist can guess at long last. But the mathematical packages refuse forthright to “excuse” these non-disclosures/omissions and give error messages. It is difficult to accuse an author, an editor, far less a proof-reader: reading closely a text is one thing, but another thing is checking carefully the formulae without using them for calculation. Numerical results are rounded in problem books and work-books and these rounded values are transferred to the following formulae that can result in errors in intermediate and final results. Mathematical packages treat non-rounded values, or rather not so much rounded results (turning to Figures 1 and 2, the value 574,7924189533622°C instead of 574,79°C, or rather 847.9424189533622 Ê instead of 847.94 Ê; the results are displayed in Celsius degrees but the program operates with Kelvin). This makes calculations more accurate but creates a problem of the difference between “live” and “non-live” work-books.
The “revival” of formulae from problem books is very useful with another respect. The network calculations checked and published on the Internet have not only educational but also practical trend because they are used to solve certain problems. In this case a work-book turns into convenient and valuable reference book.
Specification documents (for example, construction standards and regulations) can be classed as specific type of work books. There are a lot of formulae which could be revived on the Internet. Besides, the author does it within the framework of power engineering standards.
Thus, a viewer
can see one of such “live” regulatory documents, construction standards on heat
insulation depth in a heating network[26]
at http://twt.mpei.ac.ru/MCS/Worksheets/Thermal/Izol-Trub-Teploset.xmcd.
Talking about regulatory documents we should discuss certification of calculations. Fidelity of information containing in the “paper” reference books is confirmed by publishing houses with their scientific consultants, editors, and proof-readers. As a rule, the Internet pages are created without being edited and corrected. However, the author has collected a row of misprints in the reference books of respectable publishing houses, for example, 0,02387 instead of 0,02387 ( 2 was a subscript that stands for a number of repeated zeroes), or 72,93 instead of 27,39 (obviously, the number was typed by a man who spoke German, because in German “seventy two” sounds as “two and seventy” and “ninety three” — as “three and ninety”), etc. Such mistakes are practically impossible to find by traditional (visual) proof-reading of “paper” reference books. Nevertheless, the mistakes still remain with all that they imply.
There are two possible ways to certify calculation documents published on the Internet. Firstly, a trustworthy organization could confirm accuracy of calculations by a letter published on the Internet. Secondly, sites of “trustworthy organizations” could make references to the correspondent calculation sites.
4. Formula-plot and formula-table
Plots and tables in the reference books, monographs, and scientific articles are special type of formulae (hypostasis of formulae, see the title of the article).
Plots can be divided into three groups:
1. Plots constructed by certain formulae;
2. Plots constructed after statistical analysis of sampled values, or plots constructed by the formulae, which had been lost or are inaccessible now;
3. Unspecified curves (“sketches in handwriting”) given for qualitative evaluation. It is hard to calculate by them because they have no grid or points on the ordinate, they only illustrate certain dependences.
The first and the second groups of plots are easy to animate on the Internet by technology described on [2], in the chapter “A plot in a calculation site”.
Thus, Figure 5 shows a network interactive plot having relation to the first group that presents relationship between sound velocity in water/steam, pressure, and temperature.
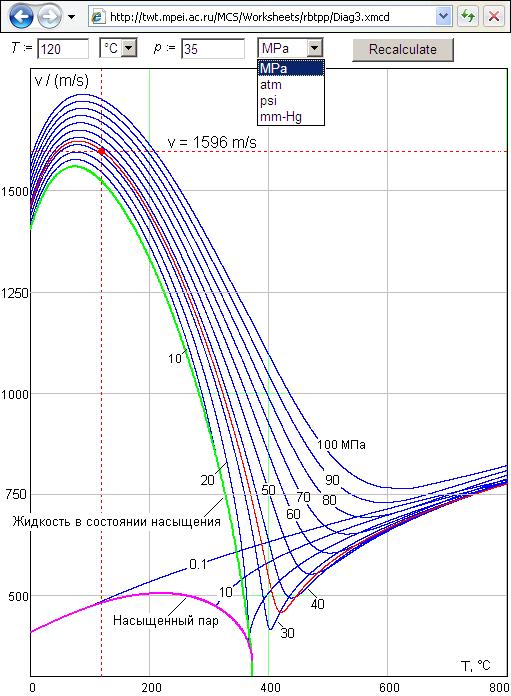
Figure 5. Plot of sound velocity in water/steam versus pressure and temperature
The isobars shown in Fig. 5 were plotted by the formulations approved by the International Association for the Properties of Water and Steam. A viewer can change initial data, click “Recalculate” button, and get not only a new numerical result (sound velocity in water/steam) but also a new isobar, new dashed lines, which fix the point of the curve. This allows him to understand in depth various laws of water/steam. There are sites that demonstrate isotherms and even surfaces in 3D space[27]. Also there is a site that shows all “live” formulae of the isobars from Fig. 5.
We can also endeavour to publish on the Internet plots from the second group that have no functional connections (digitization and obtaining discrete values on the curves, approximation or interpolation, etc.). Thus, as an example, Figures 6 and 7 show two plots: Fig.6 — sound velocity in sea water versus temperature and salinity[28], a scanned curve[29] from the reference book “Physical quantities” (Moscow, Energoatomizdat, 1991, see site at http://twt.mpei.ac.ru/PVHB with “live” calculations from this book), and Fig. 7 — the same plot, published on the Internet, which constructs wanting isoline, calculates sound velocity, and fixes the point on the curve.
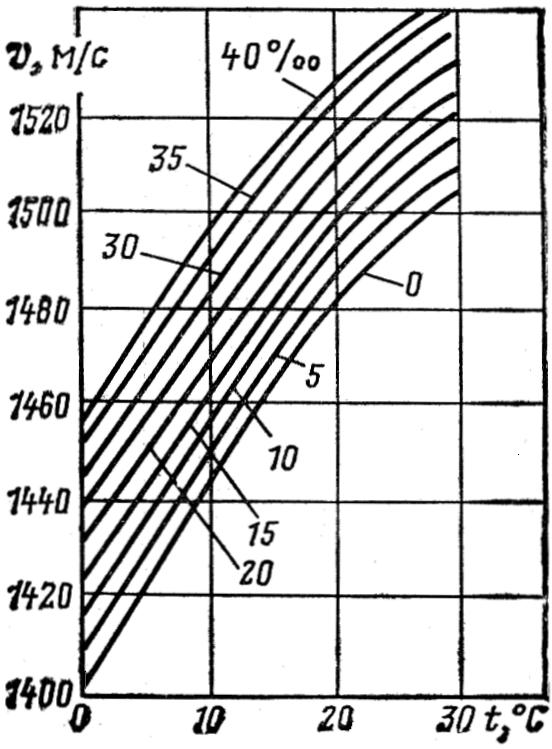
Figure 6. A typical plot from a “paper” reference book
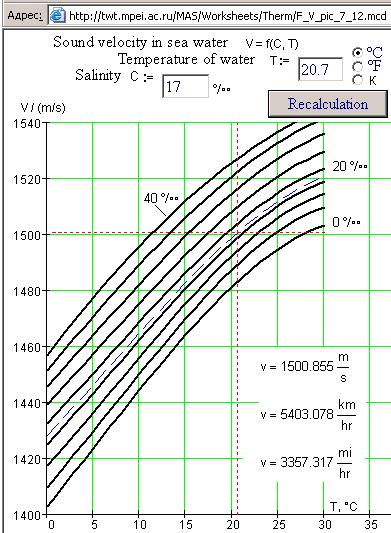
Figure 7. A typical “live” network plot
Reference materials also contain various nomograms and such prompts: mark on the first argument on the left scale, and the second argument on the right scale, draw the line between each mark and read off a result on the middle scale. In nomorgams the physical meaning of a problem disappeared (a generation of engineers used them), but accuracy of calculations increases. There were produced simple mechanical devices similar to slide rule containing the calculation algorithms. Such devices had been used by navigators laying the routes of sea-crafts and airplanes before time of on-board computers and global positioning systems. Today one can buy suchlike in news-stand – combine your weight and height on two disks and learn if it is time to go on a diet. Nomograms are easy to “enliven” on the Internet, too.
Besides formulae and plots, reference books, monographs and articles contain different tables, discrete values of functions of one, two, and three variables. The tables could be divided into two groups (not three as plots): the tables containing discrete values calculated by known formulae and tables containing empiric (experimental) values, which are not connected explicitly with formulae. The tables from the both group can be also “digitalized” and published on the Internet for interactive use. We can see a part of the table from [1] at the top of Fig. 8 containing discrete values of three bivariate functions (pressure P and temperature T) returning specific value (v), specific enthalpy (h), and specific entropy (s) of water/steam.
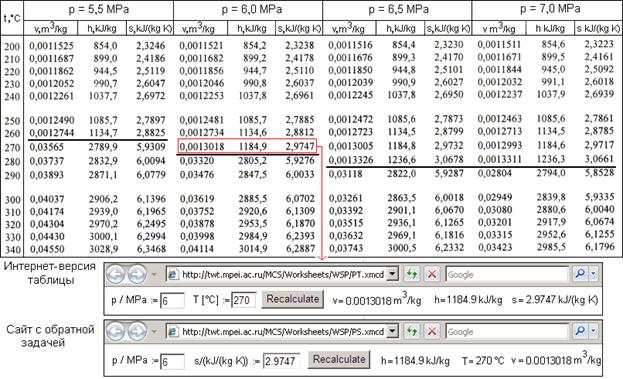
Figure 8. A table containing properties of water and steam.
In age of the Internet tables serve for filling of a reference book volume, for expansion its data sheets. Tables are of little avail for common use. For example, if one has to solve a direct problem, to find specific enthalpy from pressure and temperature (see table in Fig. 8), it can be solved quickly by simple interpolations[30]. Although, it is hard to work with the table, shown in Fig. 8 in case of an inverse problem, for example, finding specific enthalpy from pressure and specific entropy (frequently encountered heat engineering problem). In this situation the Internet calculations serve the good turn. Thus, at the bottom of Figure 8 there are two sites in which one can solve described direct and reverse problems without additional interpolations and iterations.
It beards mentioning marking of coordinate axes. In home and foreign publications if pressure plotted along the axis is expressed in megapascals, we can see marking like that: ð, ÌÐà | ð [MPa] | p / MPa ( the symbol “|” is placed here to distinguish the first comma). The last form of marking (American) could be considered as a correct one. For example, a point corresponds with value 12 and this means that p / MPa=12 or (after the pressure unit has been transferred from the left side of equation to the right side) ð = 12 ÌÐà. This rule is especially useful if dimensions contain multipliers. Let us consider a plot representing dynamic viscosity on the y-axis. The dynamic viscosity is measured in micro-Pascals multiplied by seconds: μ / (10-6 Ðà s) = 100 → μ = 100·10-6 Ðà s → μ = 0.0001 Ðà s[31]. Everything is reasonable here: the dynamic viscosity equals to one tenthousandth of a Pascal multiplied by a second or hundred microPascals multiplied by a second. This value can be inserted into the calculation. But Russian reference books contain not only right notation on the plots and tables, μ · 106, Pa·s or μ, 10-6 Pa·s, where comma means division sign, but also incorrect ones, where the comma is placed incorrectly (μ, 106 Pa· s) or an exponent sign is placed incorrectly (μ · 10-6, Pa·s). American way of plot marking is handier: in this case it is placed division sigh explicitly, not its little known “pseudonym”, a comma. Although, here incorrectness takes place: sometimes we can see a marking t / °C or Ò / °F on an American plot. The sign “/” means not division but more complicated dependence, including constants 273.15 Ê or 459.67°R. In this case it is better to write t, °C or Ò [°F], instead of t / °C or Ò / °F, where comma or brackets mean symbol of “more complicated dependence” (as shown in Fig. 5 and 7). Symbol / means division in the case of t / K or Ò / °R marking, Rankin or Kelvin absolute temperature scales .
5. Variables — physical quantities
Let us return to formula 1 and its explanation. One may often find formulae with units noted additionally in books and articles.
“Temperature (T, Kelvin) is calculated by the formula:
|
|
( 3[32] ) |
Where:
m —molar mass (gm·mol-1), p — gas pressure (Pa), v — specific volume (m3·kg-1), and R — absolute gas constant (8,314472 J·kg-1·Ê-1).”
These additional unit indications may look superfluous: if a physical value is termed there is no need to remind a reader its unit. Although…
All the formulae are known to fall into two groups by value, their external view and description: formulae connecting physical quantities and formulae connecting physical quantities with fixed units. The first group of formulae (F=a·m, E=m·c2, etc.) describes our theoretical ideas of the world around. The second group, so-called empirical formulae, describes experimental data. They have not been subjected to deep theoretical study yet that takes away “humiliating” adjective “empirical”[33]. Description of formula 3 also includes units, therefore this formula can be considered as empirical one. But it is wrong — this formula is rigorous “theoretical”, following from Clapeyron equation[34] ð·v = m·R·T[35]. Formula 3 can be considered as pseudo-empirical. Formulae of this type, coefficient-burdened, are often met in scientific and technical literature. Returning to formula 3 it will be observed that molar mass is measured not in kilogram[36] per mol as SI system demands, but by convention in gram per mol, which is settled down and fixed in various chemical and physical reference books. There is no coefficient 1000 in formula 2. Why is it so? Up-to-date mathematical packages such as Mathcad and Maple work not with values (programming languages and table processors can do this) but with physical quantities[37], mass, volume, amount of substance, temperature, etc. These packages make corresponding additional conversions of units as shown in Figure 2[38]. Moreover, these packages control dimension correspondence and, roughly speaking, do not allow a user to sum up meters and kilograms that aids in quick and correct formula input.
Coefficient 1000 in formula 3 is easy to understand — 1 kilogram equals 1000 grams. However, coefficients that allow us to utilize non-fundamental or outdated units are sometimes difficult to interpret. What is 3.6 occurring in some formulae? It is 3600 seconds per hour and 1000 kg of water per 1 cubic meter[39]. Yet, if it is required to use units aliquant to basic ones or foreign (for example, gallon instead of liter) in a formula, such coefficients become more difficult to understand. Often such coefficients are combined with constants in order to simplify calculations. Here is a typical example. All heat engineering books contain the formula for specific fuel consumption at power station:
b = 123/η, (g/kWh)
where η is efficiency of a power station expressed in absolute units.
If this value expressed in percents, the formula turns into b = 12300/η.
Substituting values into the
formula gives:
η = 0,32 b= 123/η = 123/0,32 = 384.4[40] g/kWh,
or η = 32 b= 12300/η = 12300/32 = 384.4 g/kWh.
Having efficiency of 32% the power station burns 384.4 gm of reference fuel per 1 kWh of electricity. If someone inters this formula in Mathcad and tries to calculate by it using units, the result will be dimensionless at best (see point 1 in Figure 9) or wrong at worst (see point 2).
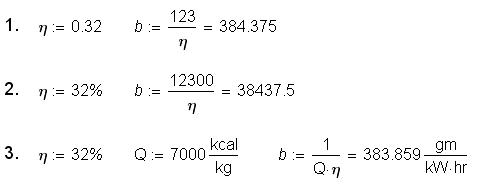
Figure 9. Efficiency of a power station calculated in Mathcad
The point is that “physical” formula of consumption of reference fuel looks like:
b = 1/(Q·η),
where Q=7000 kkal/kg, is combustion heat of reference fuel (anthracite of high quality, this value is easy to remember). Turning into SI system it was considered difficult to convert calories into joules, hours into seconds, kilograms into grams. After recalculation a new coefficient was obtained, which is also easy to remember — 123 (or 12300). As was noted before nowadays mathematical packages convert units, so the original formula[41] should be returned into reference books (see point 3 in Fig.9). It will be better if reference books contain both formula with recommendations to use the first one (b = 123/η) for manual calculations or in “non-physical” programs (calculators, programming languages, spreadsheets) and the second (b = 1/Q/η) for calculations in modern “physical and mathematical” programs that have built-in units.
The errors connecting with misuse of units have followed human in all fields of relations. For example, Peter the Great rebuked prince Kurakin in his letter of 1714 that dimensions of ships in ordered plots are smaller than required because there had been used Amsterdam feet instead of those English. In our age, the age of manmade disasters, consequences and damages of such errors could be significant.
Here are two examples concerning our time.
Boeing 767 of Canadian airlines ran from Montreal to Edmonton on 23 of July, 1983. About halfway through its flight at attitude of 12 500 the aircraft was out of fuel and it made emergency landing at a former airbase at Gimli. The cause of incident was the mistake of the pilots who miscalculated
the fuel load. At that time Canadian airlines replaced Imperial System metric system (in which volume is measured in gallons and mass — in pounds) with SI system (liters and kilograms, correspondingly). For fuel load recalculation it was required to multiply indication of fuel gauging system (in liters) by corresponding density and obtain kilograms. The pilots used previous value of density (in lbs/gal) instead of that measured in kg/L. As a result, the plane was fueled with half of required amount.
Similar mistake resulted in a failure of American orbiter Mars Climate Orbiter (MCO). It was launched on 11 of December, 1998 on a Delta-7475. The spacecraft reached Mars in 9 months, on 23 of September, 1999. At the calculated time it executed engine burn at attitude of 193 km. In 5 minutes the spacecraft passed behind Mars. The contact was never established and no further signal was ever received from the spacecraft. Findings of the failure review board indicate that a navigation error resulted from some spacecraft data being reported in Imperial units (pounds-force) instead of metric (newton). This caused the spacecraft to miss its intended 140–150 km altitude above Mars during orbit insertion, instead entering the Martian atmosphere at about 57 km. The spacecraft would have been destroyed by atmospheric stresses and friction at this low altitude. The orbiter cost 125 million dollars.
There is another engineering mistake that may be mentioned here. It is connected with relative scales rather than units themselves. It was constructed a bridge across the Rhine. One side was made by the German, the other side by the Swiss (both countries are noted to have high technology level). When spans of the bridge were to be joined it was occurred that the difference in attitudes amounted to almost half of a meter. The mistake arose from the civil design standards of zero altitude: in Germany it is level of the North Sea, in Switzerland — of the Mediterranean Sea[42].
Any specialist in any branch of science can make examples of such mistakes and cases connecting with misuse of units. This problem is solved in some degree by rejection of manual calculations and use of computer “dimensionless” program languages.
While transferring to SI system “the Augean stables were cleaned”: all formulae in new or reprinted reference and educational books were transformed so as to eliminate calories, atmospheres, kilogram-forces, and other out-of-date but widespread units. Now we generally use mathematical packages which can operate with units and this demands us “to clean the Augean stables” again. For example, it is better to give formulae in different notations considering tradition and up-to-date calculation technologies[43], supplement them with references to the Internet sites where one could calculate, make plots and get additional information unspecified in “paper” editions.
Reference books should be published and reprinted. However, current reality should be considered, particularly, the case described in this article, when it is possible to transfer from a published formula to the “live” analogue in the Internet. One may ask a “seditious” question: do we need “paper” reference books? Yes, we do, but we need reference books with the other content and form.
Mathematical packages, which can properly treat physical quantities, bring up one more peripheral question. While transferring to SI system publishing houses and magazine staff rejected manuscripts containing commonly used non-SI units. These changes were most noticeable in scientific and technical sphere where pounds, feet, etc. are used. There are some peculiarities in Russia: we will never measure pressure in pascals, more accurately, in hectopascals, but we will operate with millimeters of mercury column. Here is a summary! Mathematical packages allow us to diverge from the strict rule that ordered in articles and books only SI units to be used. We used this possible future indulgence: in Figures 1 and 2 gas pressure was entered in standard atmospheres instead of hectopascals, as an editor could demand. Figure 5 shows that to receive sound velocity in water/steam a site viewer can enter pressure in different units: megapascals, atmospheres, pounds-force per square inch, or mm of mercury column. He can also choose units for temperature: the Celsius scale[44], Kelvin, the Fahrenheit scale, degrees Rankine, or the Reaumur scale[45].
6. Empiric formulae
Let us discuss “right” empiric formulae.
Figure 10 shows work with one of them. For example, reference books on heat engineering often contain such a formula with description:
“The heat exchange coefficient (α, kcal∙m-2∙hr-1∙K-1) is calculated by formula:
|
α = 3·ð0.15·q0.7 |
( 4 ) |
where: p — pressure (technical atmosphere, kgf/cm-2) , q — heat flow (kcal·m-2·hr-1).”
As in our case, often evidence of empirical formulae is fractional values of exponents. Due to that in Mathcad the expression α = 3·ð0,15·q0,7 gives wrong result with a “strange[46] unit (see point 1 in Fig. 10).
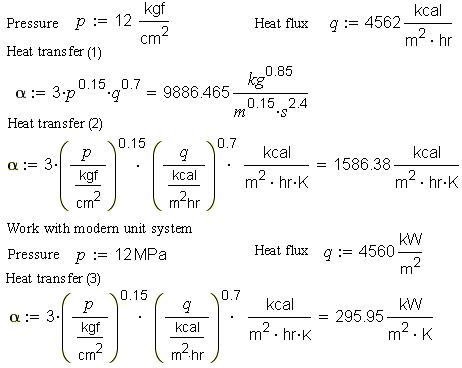
Figure 10. Empirical formula in Mathcad
The empirical formula for heat exchange coefficient was obtained by statistical analysis of experimental data. The empirical formulae always followed by notes what units should have the initial values and what units are come out. The empirical formula should be supplemented with these units. That was done in points 2 and 3: the variables were divided by their units and the formula itself was multiply by the attributable unit.
This yields a conclusion. If an empirical formula is introduced in a reference book, thinking of how it will be “enliven” in mathematical packages, it is necessary to insert units into the formula as shown in Fig. 10 rather than just mention what units should be used in it. There is no necessity to renovate such a formula, to recalculate new coefficient based on the modern system of units (which is undertaken in new reference books).
7. Mathematical operators and operators in mathematical programs
We have already discussed briefly problems of different notation of mathematical operators in reference books and in mathematical programs in section 2.
A cause of Mathcad popularity is that a user can insert mathematical operators in the way he did while studying mathematics in school and university. Due to this a Mathcad document is similar to a sheet with mathematical manipulation in script or typed in a text processor.
However, our writing style of math expression “on paper” is also changing due to the influence of mathematical packages styles. A number of people assume that it is connected with decreasing of education level. The others believe it is due to inevitable process of mathematics computerization. Thus, not relying upon the default rule the square sine is often written as sin(x)2, or (sin x)2, or (sin(x))2 , or even (sin(x))^2 instead of sin2x. There is another example. Figure 4 shows formula Q = ρ · e(…) where constant e (base of the natural logarithm) is raised to the power representing a polynomial. To avoid errors it is better to replace the exponentiation operator with the function exp: Q = ρ · exp(…). There are lots of examples when a computer has an effect on writing of mathematical expressions: 10x is replaced by ext(x), |x| – by abs(x), etc.
Special mention must be made of the mathematical symbol = (equal sign), which could be found almost in all the formulae in reference books. In mathematical packages this symbol is divided into several independent ones having their own notations.
Regarding to Mathcad, the simple note in a reference book ð = 12 MPa can have two meanings. Firstly, it means: value 12 megapascals is assigned to the variable p. In Mathcad this operation looks like: ð := 12 ÌÐà (see Fig. 10). Secondly, the expression ð = 12 MPa could mean that it is displayed numerical value of the variable p calculated above [47](displaying of the result). Equal sign can have the third meaning, Boolean operator “equal to”, that separates left and right parts of equations. For example, the famous formula F = a∙m (Newton's second law) can be considered as an expression for calculation force value (F := a·m) having a pair of known acceleration (a) and mass (m). On the other hand, it can be considered as an equation F = a∙m[48] by which we can define numerically or analytically value of a variable (F, a, or m) if two others are known. Hence, if a reference book includes a real calculation the equal sign should be treated carefully, be interpreted in different ways: as assignment symbol, displaying sign, or Boolean “equal to”.
Mathematical packages demand us to reform notations of some other mathematics symbols customary for various science disciplines, to unite them in one “computer” notation.
This thesis could be explained by an example connecting with heat engineering, formulation on thermal physical properties of ice.

Figure 11. A fragment of the formulation on thermal physical properties of ice.
Figure 11 shows the fragment of formulation on thermal physical properties of ice in the form of PDF file. The given formulation recommends how to calculate density (ρ), specific entropy (s), and specific heat at constant pressure (cp) of ice from specific Gibbs free energy (function of two arguments: pressure and temperature) by partial derivation. At that, special notation of partial derivation is used that was accepted in thermodynamics more than century ago. This notation is quite muddled: sometime (see Figure 11 column “Property”) the subscript indicates partial differentiation with respect to the variable marked in the subscript, another time, vice versa, this variable is constant (column “Relation”). There are other notations of partial differentiation in thermodynamics. What makes it more difficult to read is that only function name is noted in derivation, but arguments of a function are not listed (just g instead of g(T, p)).The same could be noted in respect with other mathematical operations and functions [49]. This confusion is the reason that students and experienced specialist make errors.
As was noted above, mathematical packages cannot put up with such defaults. Or rather, adjustable and versatile mathematical packages[50] cannot take into account all nuances and distinctions of notation of the same operator in different science disciplines. Therefore, users have to adapt themselves to capabilities of mathematical packages. Figure 12 shows an open interactive network version of formulation of ice properties. Derivate notation built in Mathcad was used there, which is clear for all users.

Figure 12. Internet formulation of thermal physical properties of ice
As shown in Fig. 12, Mathcad has got distinct symbol for partial differentiation which does not need indicating of constants. This notation style should be used in formulations, in modern educational and reference books.
References[51]:
1. Àëåêñàíäðîâ
À.À., Îðëîâ Ê.À., Î÷êîâ Â.Ô. Òåïëîôèçè÷åñêèå ñâîéñòâà ðàáî÷èõ òåë
òåïëîýíåðãåòèêè. Ì.: Èçäàòåëüñêèé Äîì ÌÝÈ, 2009
2. Êîíäàêîâà
Ã.Þ., Êîïûëîâ À.Ñ., Îðëîâ Ê.À., Î÷êîâ À.Â., Î÷êîâ Â.Ô., ×óäîâà Þ.Â. Ñïðàâî÷íîå
èçäàíèå «Èíòåðíåò-âåðñèÿ ñïðàâî÷íèêà Òåïëîýíåðãåòèêà è òåïëîòåõíèêà.
Èíñòðóìåíòàëüíûå ñðåäñòâà ñîçäàíèÿ è ðàçâèòèÿ» (ãðàíò ÐÔÔÈ 07-08-07003).
Èçäàòåëüñêèé äîì ÌÝÈ, 2007
3. Î÷êîâ
Â.Ô. Mathcad
14 äëÿ ñòóäåíòîâ è èíæåíåðîâ: ðóññêàÿ âåðñèÿ, ÁÕÂ-Ïåòåðáóðã, 2009
4. Alexandrov A.A., Ochkov V.F., Orlov K.A. Steam Tables and Diagrams on Mathcad Calculation Server for Personal Computers, Pocket Computers and Smart Phones // Proceedings of the 15th International Conference of the Property of Water and Steam, Berlin/Germany, September 7–11, 2008
5. Î÷êîâ
Â.Ô., ßíüêîâ Ã.Ã. Ìàòåìàòè÷åñêèå ïàêåòû è ïðîáëåìà ïåðåäà÷è çíàíèé // Âåñòíèê
ÐÔÔÈ, ¹ 4 (60), 2008
6. Î÷êîâ
Â.Ô. Òåïëîòåõíè÷åñêèé ñïðàâî÷íèê â Èíòåðíåòå // Íîâîå â ðîññèéñêîé
ýëåêòðîýíåðãåòèêå, ¹ 5, 2005
7. Î÷êîâ Â.Ô. Ìàòåìàòè÷åñêèå ïàêåòû è ñåòåâîé èíòåðàêòèâíûé
òåïëîòåõíè÷åñêèé ñïðàâî÷íèê: ïðîáëåìû è ðåøåíèÿ // Òåïëîýíåðãåòèêà, ¹ 6, 2006

