Этюд 3.
Взгляд на Mathcad шутника, дериватора и эстета
Пример
1. Поиск корня алгебраического уравнения
Рис.
3.2. BASIC-программа поиска корня уравнения
Примеры
2-4. Задачи старушки «Наири»
Рис. 3.3.
Поиск минимума у двухмерной экспоненциальной функции
Рис.
3.4. Поиск минимума у функции Розенброка
Рис.
3.5. Поиск минимума у функции Пауэла
Пример
5. Черный круг в черном квадрате
Рис.
3.6. Подсчет числа p
методом Монте-Карло
Пример
6. Объем конуса, или Pointiller
Рис.
3.7. Подсчет объема конуса
Рис.
3.8. Ваяние на компьютере
Пример
7. Максимальный объем пожарного ведра
Рис.
3.9. Задача о пожарных ведрах: перебор
Пример
8. Как автор продавал программы
Рис.
3.10. Определение плана выпуска стульев: перебор
Пример
9. Опять задача старушки «Наири»
Рис.
3.12. Поиск места для ларька
Задача
коммивояжера и ее решение в среде Mathcad (функция anneal
из e-book «Численные методы)
Рис.
3.13. Транспортная задача (извращенное решение)
Пример
10. Mathcad и булевы (логические) функции (English version of text)
Рис. 3.14.
Логические операторы и функции
Автор
надеется, что читатель заинтригован названием этюда. Смысл термина дериватор
будет раскрыт в своем месте и в свое время[1].
3.1. Взгляд шутника
Есть особый
род шутников (к ним относит себя и
автор), получающих удовольствие от попыток розыгрыша компьютера. «Много ты, машина, о себе воображаешь. Посмотрим-ка, проглотишь ли ты вот это?!», – так или
примерно так думают они, вводя в ЭВМ заведомо «неправильную» информацию. Анализ
реакции компьютера (программной среды) на подобные шутки пользователя может
дать не меньше, чем классический разбор программы.
В
этюде будет рассмотрено решение в среде Mathcad задач из области вычислительной
математики. Примеры взяты не из пакета Mathcad (хотя там есть схожие задачи), а
из других источников, и подобраны так, чтобы можно было показать не только
легкость и изящество их решения, но и возникающие при этом осложнения и пути их
преодоления. К примерам, которые прилагают к пакетам фирмы-разработчики,
следует относиться с большой опаской. Тут можно вспомнить эпохальную
вычислительную машину «Наири», в матобеспечении
которой была программа «Поиск минимума функций». Так вот, после опробования
слово функций (множественное число) в
ее названии приходилось менять на слово функции
(единственное число), так как минимум искался только у приложенной к программе функции и больше ни у какой другой.
Пример 1. Поиск корня алгебраического уравнения
Есть хорошее правило: при
отладке и испытании программы нужно подсунуть ей задачу, решение которой
заранее известно.
На рис. 3.1
с помощью встроенной функции root ищется корень кубического уравнения, записанного в
пункте 1. Из графика (пункт 2) анализируемой функции y(x) и из
результата работы функции polyroots (пункт 3) видно, что у нее один действительный корень,
который легко найти и с помощью функции root, если
начальное приближение к корню равно, например, минус 50 (пункт 4).
Рис. 3.1. Поиск корня уравнения
Теперь мы подшутим
над функцией root, и если не получим от этого удовольствия, то хотя бы
уясним себе, какие «подводные камни» могут нас ожидать.
Если в качестве первого
приближения (опорной точки) принять не минус 50, а плюс 5 (пункт 5), то функция
root выкинет
«белый флаг»: сообщение «Can’t converge to a
solution», отказываясь решать поставленную задачу, хотя плюс 5
намного ближе к корню, чем минус 50. Вот вам и первое приближение! Но это еще полбеды. Настоящая беда случается тогда,
когда функция root (как, впрочем, и некоторые другие функции и операторы
Mathcad) не отказывается решать поставленную задачу, выдавая при этом неверный
результат (феномен медвежьей услуги).
Если функцию y(x) умножить
на константу, например на 10-5, то ее корни останутся на старых
местах. Но это утверждение в среде Mathcad не является истиной – см. пункт 6
рис. 3.1.
Не то беда,
Авдей Флюгарин,
Что родом
ты не русский барин,
Что на
Парнасе ты цыган...
Беда, что
скучен твой роман.
Не то беда, что ты, Mathcad, неправильно решил
простейшую задачу: и более мощные специализированные пакеты, ориентированные
только на решение алгебраических уравнений и систем, делают тут промах. Беда в
том, что Mathcad в этом честно не признался, как это было в пункте 5 на рис.
3.1.
Философский смысл любой
шутки заключается в том, что у шутника и у того, над кем подшучивают, разные
понятия о природе вещей. У пользователя и у среды Mathcad
разные понятия о том, что такое корень
уравнения: человек считает, что корень – это то значение аргумента, при
котором выражение равно нулю; функция же root
«считает», что корень – это то значение аргумента, при котором значение
выражения по модулю не превышает значения системной переменной TOL,
которая по умолчанию равна 10-3. Отсюда и путаница в пункте 6
на рис. 3.1. Чтобы функция root там сработала правильно,
необходимо переменной TOL присвоить
новое значение (10-7, например), заменив им предопределенное. Можно
поступить и по-другому – умножить в пункте 6 правую часть функции на 100 000, убрав тем самым коэффициент 0.00001. Метод
балластных (нормирующих) коэффициентов особенно эффективен при решении
алгебраических систем (что уже было отмечено в этюде 1). Он позволяет уравнять
все уравнения (прошу простить за тавтологию) по отношению к точности, с которой
система решается через блок Given-Find. На нижнем
графике рисунка 3.1 ось X «утолщена»
до значения TOL (пунктир).
Корень там, где кривая касается этой «толстой» оси.
В среде
Mathcad 8 переменная TOL была
дополнена еще одной системной переменной ¾
CTOL (tolerance of the
constraints
¾ точность
ограничений), которая
также по умолчанию равна 10-3, но уже отвечает не за поиск корней и
оптимумов, а за ограничения ¾ за
уравнения и неравенства, записанные после ключевого слова Given.
С промахом, зафиксированным
в пункте 5 рис. 3.1, можно разобраться после знакомства с вычислительными
методами, заложенными в функцию root. В Руководстве
пользователя Mathcad сказано, что функция root ищет
корень выражения методом секущих, и
дано его описание, которое автор перевел на язык BASIC.
' Поиск корня уравнения методом секущих
' Реализация на языке BASIC Mathcad-функции root
Def FnY(x) = 2 * X ^ 3 + 20 * x ^ 2 – 2 *
x + 100 ' Анализируемая функция
TOL = 0.001 ‘ Точность поиска корня
‘ Начало процедуры поиска корня
Input "X нач. :=", X ‘
Начальное приближение
If Abs(FnY(X)) < TOL Then
root = X ‘
Начальное приближение и есть корень уравнения
Else
‘ Расчет второй опорной точки
If X
= 0 Then h = TOL Else h = X * TOL
X0 = X
: X1 = X + h
Do ‘ Цикл приближения к корню
root = X1 – FnY(X1)
* (X1 – X0) / (FnY(X1)
– FnY(X0))
X0 = X1: X1 = root ' Подготовка к
следующему приближению
Loop Until Abs(FnY(X1)) <=
TOL ‘ Условие завершения цикла
End If
Print
"Y=0 при X="; root ‘
Вывод результата
Рис. 3.2. BASIC-программа поиска корня
уравнения
Проанализировав эту программу, можно понять, почему
корнем другого уравнения Y
= X2 - 4 при нулевом (симметричном –
проблема Буриданова осла) начальном приближении оказывается плюс, а не минус 2:
x := 0 x
:= root(X2 - 4, X) x = 2
Хотя в BASIC-программе полностью реализован метод
секущих, описанный в Руководстве пользователя, но...
Во-первых, в вышеприведенную BASIC-программу не заложено никаких
сообщений об ошибках, а функция root его выдает
(см. пункт 5 рис. 3.1). Во-вторых, BASIC-программа, в отличие от функции root, прекрасно
нашла корень уравнения y(x), заданного в пункте 1, от начального приближения,
равного плюс 5. И, в-третьих, в BASIC-программу заложен не метод секущих, а
комбинированный метод Ньютона-секущих.
Классический метод секущих требует задания не одного, а двух начальных значений
аргумента: через одну точку проводится касательная (метод Ньютона), а через две
– секущая. Вот так мы разобрались с функцией root! Хотели
над ней подшутить, а она сама над нами посмеялась.
В этюде 6
читатель может найти функции пользователя для поиска корней уравнений методом Ньютона, методом половинного деления и методом секущих,
ориентированные по точности не на значение анализируемой функции (Do ... Loop Until Abs(FnY(X1)) <= TOL – см. программу на рис. 3.2), а на
значение аргумента (Do ... Loop Until Abs(X1
– X0)
<= TOL, например). На такую подмену приходится идти, решая
реальную задачу. Так, например, в коллекции автора есть учебная программа
определения значения рН раствора, где рН ¾ это корень
уравнения электронейтральности раствора (баланс
катионов и анионов). Но нас мало интересует дисбаланс ионов (отклонение
анализируемой функции от нуля) ¾ главное,
чтобы новое значение рН отличалось от предыдущего не
более чем на величину 10-3 (обычная точность рН-метра).
Примеры 2-4. Задачи старушки «Наири»
В специальной литературе приводятся три функции (двухмерная экспоненциальная функция,
функция Розенброка
и функция Пауэла),
с которых рекомендуется начинать тестирование программных средств поиска
минимума. Если программа эту тройку «разъяснит», то... можно проводить
следующие испытания. Если же тест закончится неудачей, то... А что, собственно,
то? На этот счет нет единого мнения.
Одни считают, что такую программу поиска минимума нужно отбраковывать. Другие
же полагают, что отдельный промах еще ничего не значит: «Скажи мне, на какой функции твоя программа споткнулась, и я скажу,
какой алгоритм в нее заложен и как его можно доработать».
Сейчас мы
попытаемся протестировать все три средства поиска минимума, интегрированные в
Mathcad, на трех вышеописанных функциях. Испытаниям подвергнется не только
пакет Mathcad, но и сам пользователь: любой инструмент сам по себе ничего не
значит – работать он может только в умелых руках.
Недостаток всех тестовых
функций заключается в… их сущности – в том, что испытующий заранее знает ответ.
Экзаменуя программу, пользователь как бы подталкивает ее к ответу, нарушая тем
самым чистоту эксперимента.
Но, как мы полагаем, не все
наши читатели знают, где три функции:
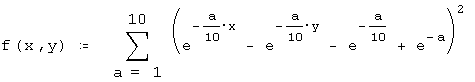 (двухмерная экспоненциальная)
(двухмерная экспоненциальная)
![]() (Розенброка)
(Розенброка)
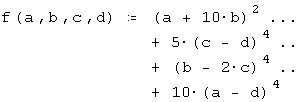 (Пауэла)
(Пауэла)
имеют минимумы. Поэтому мы предлагаем читателям
сначала попытаться найти их самим. Это будет проверкой не только и не столько
пакета Mathcad (а он с тестовой тройкой функций более-менее справился – не
смотрите пока на рис. 3.3-3.5), сколько нашего читателя. Тем более что с
оптимизацией он уже натренировался «на кошечках» – на ведрах и коробках этюда
2.
(Пауза в чтении книги, связанная с самостоятельной
оптимизацией читателями в среде Mathcad тройки тестовых функций ¾
контрольная по этюду 2).
Рис. 3.3. Поиск минимума у двухмерной
экспоненциальной функции
Двухмерная экспоненциальная
функция имеет минимум (нулевое значение) при x=1 и y=10. Это
хорошо видно в пункте 1 на рис. 3.3, где показаны поверхность и линии уровня
вблизи минимума[2]. Эти
графики несложно построить, если, конечно, знаешь, где находится минимум,
охватываемый переменными x1, x2, y1 и y2. Поверхность развернута так
(см. ее координаты на фрагменте окна редактирования), чтобы линии уровня
являлись проекцией поверхности на
горизонтальную плоскость.
В пункте 2 при поиске
минимума в качестве начальных приближений давались точки, расположенные по
углам прямоугольника ¾ области
существования аргументов на графиках. Так испытывалась сходимость метода поиска
минимума. Зафиксирована всего лишь одна осечка: при начальном приближении x=1.2 и y=14 не был
найден корень системы, состоящей из приравненных к нулю частных производных двухмерной
экспоненциальной функции[3].
Рис. 3.4. Поиск минимума у функции Розенброка
Функция Розенброка
примечательна тем, что ее минимум невозможно увидеть ни на линиях уровня, ни на
поверхности (пункт 1 на рис. 3.4). Скажем осторожнее – автору не удалось этого
сделать. На графиках просматривается типичный овраг, где анализируемая функция в одном направлении изменяется
круто, а в перпендикулярном – слабо. Этим пытаются как бы дезориентировать программу поиска минимума –
на то и создаются тестовые функции. Графики строились по новой, третьей
технологии ¾ задавался
центр (x и y) квадрата
со стороной 2D области существования аргументов на графиках. Вторая
технология ¾ это когда
задаются координаты углов прямоугольника существования аргументов на графиках
(см. пункт 1 на рис. 3.3). Первая технология (кстати, самая неудобная для
понимания) была использована, например, в рис 2.8 – там область размаха
поверхности завуалирована в значениях переменных i и j.
В пункте 2 на рис. 3.4 поиск
минимума велся от трех начальных точек (10-10, 100-10 и 100-100) тремя
способами. Итоги «соревнования»: на первом месте по-прежнему функция MinErr, которая выдавала абсолютно точный
результат (пару единиц). На втором месте функция Minimize
c относительно
правильными ответами. Функция же Find сошла с трети дистанции – только при первом приближении
был выдан относительно точный результат. Здесь, по-видимому, с функцией Find овраг сыграл
злую шутку.
Функция Розенброка
имеет минимум (нуль) при x=1 и y=1. Через эту точку можно
провести секущие плоскости и показать
на декартовых графиках, что функция там минимальна (см. пункт 3 на рис. 3.4),
ее частные производные равны нулю, а частные производные второго порядка
положительны.
Рис. 3.5. Поиск минимума у функции Пауэла
Функция Пауэла
(рис. 3.5) имеет четыре аргумента. Следовательно, в трехмерном мире – даже
виртуальном – никакими поверхностями и линиями уровня минимум (нуль) функции Пауэла не локализовать (не визуализировать). Проверить соответствие найденной точки (четыре нуля) минимуму можно
либо через декартовы графики сечений по технологии рисунка 3.3), либо через
линии уровня, что и было сделано в пунктах 2.1 и 2.2 на рис. 3.5. Для
этого две координаты фиксируются на нулевых значениях, а две другие изменяются
вокруг нуля (нули – это координаты минимума). Таких топограмм
четырехмерной функции можно построить шесть штук следующих пар аргументов: a0-a1, a0-a2 (см. рис.
3.5), a0-a3, a1-a2, a1-a3 и a2-a3 (по четырем
последним парам читателю предлагается построить топограммы
самому). Решение по функции Пауэла более-менее удачно
велось с помощью функций MinErr и Minimize. Поиск корня системы четырех алгебраических уравнений – частных производных
функции Пауэла – здесь применить нельзя, так как
переменные анализируемой функции у нас не скалярные величины (с именами a, b, c и d,
например), а одиночная переменная-вектор с именем a. По
индексным переменным производная в среде Mathcad не высчитывается. Читатель при
желании может переопределить функцию Пауэла
(задействовать в ней четыре переменные-скаляра)
и решить задачу с помощью частных производных. Так, кстати, решалась эта задача
в предыдущих изданиях книги.
Выводы по испытаниям трех
функций – в конце этюда.
3.2. Взгляд дериватора
Есть особый род извращенцев… Автору не хватило духа
вынести этот термин в заголовок этюда, и он заменил его нейтральным,
производным от латинского derivatio (отклонение). Читатель, может быть, до этого места книги не
доберется, а об авторе подумает черт знает что. Так
вот, есть особый род дериваторов,
получающих удовольствие от попыток решения задач программными средствами, для
этих целей прямо не предназначенными.
– А вы ноктюрн сыграть смогли бы на
флейте водосточных труб?!
– А вы тра-та-та та-та-ра-та бы в среде программы тра-та-та?!
Пример 5. Черный круг в черном квадрате
Имея под
рукой ЭВМ, можно проводить расчеты по алгоритмам, на реализацию которых в докомпьютерную эру решались только одержимые какой-то идеей
единицы (своего рода дериваторы). Из
литературы известно, что французский естествоиспытатель Бюффон (XVIII век)
подбросил монетку 4040 раз и подсчитал, что орел выпал 2048 раз, а решка – 1992. Английский статистик К. Пирсон описал серии
бросаний монеты в 12 000 и 24 000 раз. В первом случае орел выпал 6019, а во
втором – 12 013 раз.
Тот же
Бюффон определил число p очень
интересным способом: провел на большом листе бумаги параллельные равноотстоящие
прямые линии, стал бросать на него случайным образом иголку длиной, равной шагу
между линиями, и подсчитывать общее число бросаний (N) и число попаданий иголки
на одну из линий (n). Теория вероятностей подсказывает, что в отношении n/N заложено число p, которое и пытался
определить Бюффон столь необычным способом.
Найти, например, значение
определенного интеграла методом статистических испытаний (или методом
Монте-Карло, так по-другому называют методы расчетов, использованные Бюффоном и
Пирсоном) можно следующим образом. Нужно в прямоугольник вписать график
интегрируемой функции и бросать в него случайным образом ... камешки. Козьма
Прутков в подобной ситуации, но когда камешки бросались в воду, рекомендовал смотреть на круги, ими образуемые; иначе
такое занятие будет пустою забавою. Воспользуемся советом, но будем считать
не круги, а количество попаданий камешков под график. Отношение числа попаданий
(n) к общему
числу бросков (N) должно
хранить значение интеграла, если верить теории вероятностей.
Итак,
бросаем «камешки в воду».
Рис. 3.6. Подсчет числа p методом Монте-Карло
Есть более простой способ
статистического расчета числа p, чем тот,
который использовал Бюффон. Можно нарисовать квадрат, вписать в него круг
(«квадратура круга») и бросать туда камешки. Так как в площади круга запрятано
число p («пи эр в
квадрате» – вспомним старый анекдот о том, почему у поезда колеса стучат), то
через подсчет попаданий в круг можно оценить число p. Бюффон этот метод не использовал наверное из-за того, что трудно добиться
равномерного попадания камешков в квадрат.
На рис. 3.6
зафиксирована оценка площади круга, вписанного в квадрат, и сделана попытка
расчета значения числа p. Как это
делалось?
В пункте 1
на рис 3.6 формируются два вектора X и Y, элементы
которых (а их 7000) ¾ случайные
вещественные числа в интервале от минус до плюс единицы. X и Y – это по своей
сути координаты точек случайного падения камешков в квадрат размером 2 на 2.
Далее в пункте 2 эти камешки сортируются на «чистых и нечистых»: координаты точек, попавших в круг,
дублируются в векторах
Xo и Yo (o ¾
попал), а не попавших ¾ в векторах Xx и Yx (x
¾ промах).
После этого несложно визуализировать попадание точек в круг с помощью
параметрического декартового графика. Достаточно при форматировании графика
указать, что линий нет, а есть одни точки. При этом точки, попавшие в круг
(вектора Xo и Yo), более
толстые. Теперь для оценки числа p можно подсчитать число попаданий камешков в круг (пункт 4) ¾ число
ненулевых элементов вектора
Xo (или Yo). В пункте
5 число p
рассчитывается и сравнивается с его точным значением.
Функция rnd в среде
Mathcad имеет аргумент, отличающийся от своих аналогов на языках
программирования. В среде BASIC или Pascal аргумент
функции rnd связан с
приставкой псевдо- в ее названии, а не с диапазоном
генерируемых случайных чисел. Да, числа генерируются случайные, но ряд этих чисел
псевдослучаен, так как его в любой
момент можно повторить. За такой
повтор на языках программирования отвечает аргумент функции rnd, а в среде
Mathcad – число (по умолчанию это 1), хранящееся в окне Seed value for
random numbers (инициализация генератора
случайных чисел) ярлыка Built-in Variables окна Math
Options, которое вызывается на
дисплей командой Options
в меню Math:
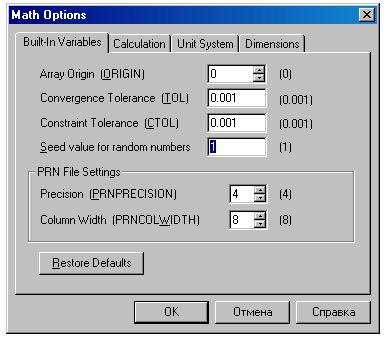
От истинно случайных чисел отказались еще на
заре развития компьютерной техники, когда пытались встраивать в ЭВМ что-то
похожее на рулетку. Но это устройство
оказалось слишком неповоротливым, а главное, с его помощью невозможно было
получать повторяющиеся ряды случайных (псевдослучайных) чисел, что необходимо
при отладке программ. Поэтому
генерированию случайных чисел на физических моделях (рулетка) предпочли их
математическое моделирование. Какой алгоритм заложен в функцию rnd,
пользователя волнует мало – главное, чтобы ряд генерируемых чисел не вырождался,
а сами числа распределялись в заданном диапазоне равномерно[4],
в чем можно убедиться визуально – см. пункт 3 рис. 3.6.
Наш подсчет числа p методом Монте-Карло (а рулетка была не зря упомянута) – это
чистой воды извращение (пардон,
деривация): то же число p (или интеграл) легко можно
рассчитать напрямую – конец пункта 5. Но все-таки наше извращение было не таким
уж извращенным.
Во-первых, решив задачу на
рис. 3.6, мы, по сути, не рассчитали значение p, а проверили качество
генератора псевдослучайных чисел, то есть добротность встроенной функции rnd. При числе
бросаний «камешков в воду», стремящемся к бесконечности,
ошибка метода Монте-Карло должна стремиться к нулю, если функция rnd работает
правильно.
Во-вторых, есть фигуры,
площади которых невозможно рассчитать традиционными методами, без «извращений».
Пример – площадь облака на снимке из космоса. Эту площадь довольно точно и,
главное, быстро (в метеорологии вчерашний прогноз никому не нужен) можно
определить, ткнув случайным образом несколько раз в фотографию иголкой, и… см.
рис. 3.6.
Традиционные способы
подсчета площади фигуры (интеграла) тут не годятся не только потому, что
контуры облака невозможно описать какой-либо интегрируемой функцией, но и из-за
того, что они размытые, нечеткие.
В математике, самой точной
на свете науке, появилось новое направление: теория нечетких множеств (другой
термин – «размытые множества», но по-английски это звучит более поэтично: «fuzzy sets» – пушистые множества[5]).
Эта теория оперирует такими «перлами», как «скорее
1, чем 2», «скорее плюс, чем минус», «точка находится скорее под графиком, чем
над ним» и т.д. В основе теории нечетких множеств лежит знаменитый софизм: «Если к горсти зерна добавить еще одно
зернышко, превратится ли она в кучу? А если добавить два зерна? А сколько зерен
превратят горсть в кучу?» Это самое сколько
– типичный представитель fuzzy set,
к которому трудно приложить и современную теорию чисел, и саму цифровую
вычислительную технику. Программирование же – это по своей сути жонглирование
нулями и единицами, то есть крайняя категоричность мироощущения, когда все
богатство цветов и оттенков сводится к черному и белому. Мир же состоит не из
чисел, а из куч, горстей, облаков, то есть из нечетких множеств, к обсчету которых современные компьютеры приспособлены
очень плохо. Кто поднимался на самолете сквозь облака, знает, что никакой
границы между облаком и не облаком нет. В этом-то, по-видимому, и будет
заключаться один из будущих кризисов теории программирования и вообще
элементной базы компьютеров. К теории нечетких множеств мы еще вернемся в конце
этого этюда в главке о четкой и нечеткой логике и в этюде 6. А пока задание
читателю – реализовать в среде Mathcad метод подсчета числа p, предложенный Бюффоном.
Поэтому повторяю – наше
извращение на рис. 3.6. было не таким уж извращенным.
Можно сказать, что на рис.
3.6. мы, подражая Казимиру Малевичу, нарисовали «Черный круг в черном
квадрате». Так мы невольно вторглись в Мир Искусства…
Считается, что искусство
зиждется на трех китах. Вот они: чувство
меры, воображение и ... потребность в извращениях, связанная с сомнениями и творчеством.
Теперь о сомнениях.
Пример 6. Объем конуса, или Pointiller
От выпускников авиационных
вузов часто можно услышать, что они так и не уяснили себе, как железный самолет
может летать. Многие финансисты с высшим образованием не понимают (душой не
принимают), как могут функционировать безналичные расчеты. Послать деньги в
конверте по почте, ну, пусть не золото, а его заменитель (бумажные деньги), –
это еще куда ни шло. А вот как деньги могут
передаваться по проводам (безналичные расчеты, торговля через Internet и др.) – это уму
непостижимо!
Автор в школьные годы очень
сомневался в том, что сумма углов треугольника равна 180 градусам. Чтобы
развеять сомнения, он (автор) нарисовал чуть ли не
тысячу треугольников, измерил транспортиром и просуммировал их углы! Но
сомнения все равно остались, благо на то есть основание – неевклидова
геометрия.
Очень сомнительно, что объем
конуса (а на нем построен целый этюд книги – этюд 2) составляет ровно треть от объема цилиндра, в который этот конус вписан (см. данные
из справочника Mathcad на рис. 2.1). Давайте проверим это.
Рис. 3.7. Подсчет объема конуса
На рис. 3.7 не только рассчитан
объема конуса методом Монте-Карло, но и дано изображение самого конуса. В
изобразительном искусстве есть направление, называемое пуантилизм (от французского pointiller –
писать точками). Его последователи формируют картину отдельными мазками правильной
точечной или прямоугольной формы. Мы уже нарисовали в такой манере «Черный круг
в черном квадрате». «Натюрморт с конусом», выполненный в этом же стиле, можно
увидеть в пункте 3 рис. 3.7. Здесь «поработал» Scatter Plot
– трехмерный точечный график. Так незаметно мы перешли
от двухмерной к трехмерной графике – от живописи к… скульптуре.
Рисовался (вернее, ваялся)
конус так. В прямоугольный параллелепипед размером 2 на 2 на 1 бросались
случайным образом «камешки» – формировались три вектора X, Y и Z, элементы
которых – случайные числа в диапазоне минус единица – плюс единица (векторы X и Y) и ноль –
единица (вектор Z см. пункт
1 на рис. 3.7). Далее точки, не вписывающиеся в конус, отсеивались:
соответствующим элементам вектора Z присваивалось значение бесконечности (пункт 2), и
они... «улетали на небо», формируя линию над конусом (пункт 2).
Пункты 3 и 4 – это подсчет
объема конуса методом Монте-Карло и сравнение его с истинным объемом конуса[6].
Сомнения остались, но очень незначительные – в пределах ошибки метода
Монте-Карло.
Один великий художник
сказал, что ваять очень просто – берется глыба мрамора и от нее отсекается все
лишнее. «Всякий талант неизъясним. Каким образом ваятель в куске каррарского мрамора видит сокрытого
Юпитера и выводит его на свет, резцом и молотом раздробляя его
оболочку?»[7]
А вот еще одно парадоксальное высказывание: «Играть на фортепиано очень просто.
Достаточно в нужный момент нажимать нужные клавиши!» Все это можно
рассматривать как некую браваду или как попытки Художника подурачить публику,
пристающую с «глупыми» вопросами о тайне творчества. А можно принять за
руководство к действию. С живописью мы разобрались (см. рис. 3.6) – возьмемся
теперь за скульптуру.
На рис. 3.7 у нас есть
«глыба мрамора» размером 2 на 2 на 1, от которой также отсекается лишнее (осколки падают не на пол, а улетают на небо). Пока у
нас «изваялся» простой конус, но ничто не мешает нам
усложнить формулы в пункте 2 на рис. 3.7 и слепить Венеру Милосскую
или Мыслителя Родена… На рис. 3.8 дается методика
ваяния человеческой фигуры.
Рис. 3.8. Ваяние на компьютере
Автор пока поступил проще.
Он через команды форматирования графика окрасил точки конуса на рис. 3.7 в
зеленый цвет, подбросил еще несколько точек красного цвета и большего диаметра.
Поучилась неплохая новогодняя елка.
Сейчас компьютер широко
используется как рабочий инструмент художника (интеллектуальная кисть или
что-то в этом роде). Распечатки цветных принтеров оправляются в рамки и
выставляются в, так сказать, реальных и виртуальных компьтерно-художественных
салонах (см., например, журнал «КомпьюАрт»).
Но автору
хотелось бы обратить внимание уважаемых читателей на другое – на проблему
эстетического вида не просто компьютерных рисунков, а листингов программ и, в частности, на проблему соответствия (или
противопоставления) формы листинга содержанию программы.
Программисты, которым не
чуждо образное мышление, давно уже подметили, что процедуры и функции имеют
свое собственное «лицо», по которому она безошибочно узнается на экране дисплея
или на бумаге принтера. Одна процедура как ухоженная крестьянская лошадка
круглая и гладкая – работает себе спокойно, перекачивая, например, данные из
одного формата в другой. И внешне она неприметна – взгляд на ней не останавливается. Другая
процедура все время норовит выкинуть какой-нибудь фортель, настолько она неотлаженна (необъезженна). И своими очертаниями она
походит на скакуна, в седле которого сидит герой многочисленных живописных
полотен и скульптур. Третья процедура так и просится, чтобы ее оправили в раму
и повесили на стену, настолько она хороша и закончена, а главное, ее форма
полностью отвечает ее содержанию. Она передает не только мысли, но даже и настроение
художника, пардон, программиста, ее создавшего.
Автор далеко
не искусствовед и не смеет особо распространяться на эту тему.
В комментариях к публикуемым
компьютерным рисункам, как правило, подчеркивается, что их авторы – компьютерные художники. В прилагательных
к существительным очень часто таится некая ущербность
или по, крайней мере, двусмысленность: не просто математика, а «Прикладная математика» –
см. главку «Mathcad и Maple» в этюде 7. Термин компьютерный художник содержит в себе некую двойственность. С одной
стороны, прилагательным «компьютерный» как бы извиняются перед потенциальным
зрителем за эстетику рисунков (см. наши «рисунки» 3.6 и 3.8). А с другой
стороны – предупреждают о том, что при создании рисунков использовались
специфические инструменты и методы (авангардистские изыски).
Настоящий художник готов
работать на чём угодно и чем угодно. Рисунки Анатолия Зверева
(художника с трагической судьбой, какая, увы, часто постигает гениев),
выполненные чуть ли не окурком на обрывке листа бумаги, продаются на аукционах
за большие деньги. Давайте дождемся времен, когда распечатки принтеров будут
выставляться в Лувре, в Эрмитаже или на худой конец продаваться на
художественных аукционах. Последнее вряд ли случится. На аукционах могут
продать дискету, принадлежавшую компьютерному художнику (фетиш – сейчас так продаются
гитары великих музыкантов). Дело в том, что у computer
art нет понятия оригинала
и копии[8].
А это может убить даже настоящие шедевры, которые иногда публикуются на
обложках и внутри глянцевых изданий. Пушкин говорил: «Пóшло то, что пошлó в народ». Только самые гениальные
произведения искусства способны выдержать такое испытание хождением в народ.
Они-то и формируют пласт культуры, на котором базируется современная
цивилизация.
Лучший способ охарактеризовать какое-либо явление – тем более в книге с претензией на искусствоведение – это привести классическую цитату. Вот она:
Они сначала
нравилися мне
Глазами
синими, да белизною,
Да
скромностью – а пуще новизною;
Да, слава
богу, скоро догадался –
Увидел я,
что с ними грех и знаться –
В
них жизни нет, все куклы восковые;
А
наши!...
Угадайте, о чем говорил
пушкинский Дон Жуан! Да-да – и о компьютерной анимации, о рисунках, созданных с
помощью компьютерной графики... Скажем мягче (и с надеждой) – о современных
образцах этого симбиоза науки, технологии и искусства. Ведь, в компьютерных
рисунках больше чувствуется несовершенный инструмент (новизна – парадокс high
technology), чем
художник.
Пример 7. Максимальный объем пожарного ведра
Очень близок к методу
Монте-Карло (не только по идеологии,
но и по длительности реализации)
другой метод, получивший второе дыхание в эпоху компьютеров, – метод перебора. Если задача имеет ограниченное
число вариантов ответа, то, не мудрствуя лукаво, можно все их просчитать и
выбрать подходящий. Как долго будет длиться такой
перебор и как его можно ускорить – ответы на эти вопросы мы дадим в этюде 6.
Наша старая задача о пожарном ведре максимального объема (см. рис. 2.2) может быть решена методом перебора с учетом того факта, что точность раскроя круглой заготовки, равная одному угловому градусу, – предел мастерства даже трезвого жестянщика.
Рис. 3.9. Задача о пожарных ведрах: перебор
В решении задачи о пожарных
ведрах на рис. 3.9 в пунктах 1 (одноведерная задача)
и пункт 2 (двухведерная задача) формируются векторы a, V и V2 по 361 элементу в каждом[9].
Ключевой оператор решения использует встроенную функцию max,
возвращающую максимальное значение своего аргумента – вектора (матрицы).
Функции, возвращающей номер максимального элемента вектора (матрицы), в среде
Mathcad нет – с рассуждениями по этому поводу читатель может ознакомиться в
этюде 4. Поэтому на рис. 3.9 (как и на рис. 3.6 и 3.7) задействован оператор
суммы, перебирающий все варианты
ведер и запоминающий угол вырезки для изготовления одного ведра максимального
объема – 66 градусов (пункт 1) или двух ведер с максимальным суммарным объемом
– 117 и 243 (360-117) градусов (пункт 2). Наш метод перебора опасен тем, что
если у вектора (матрицы) два и более максимальных значений (как у вектора V2), то в
лучшем случае появится сообщение об ошибке, а в худшем – неправильный ответ
(см. пункт 2 на рис. 3.9 с aопт[10]=360). При
решении трехведерной задачи (пункт 3) на область максимума была
как бы наброшена сетка, в узлах которой просчитаны значения «трехведерной»
функции. Далее были определены координаты сетки, где данная функция
максимальна. Такой контрольный расчет перебором еще раз показал, что третье
ведро лишнее – мы получили уточненное решение двухведерной задачи из пункта 2.
Наше решение выглядит
несколько извращенным – в функцию max,
составляющую ядро расчета на рис. 3.9, и в другие, ей подобные, также заложен
перебор: что-то другое здесь вряд ли придумаешь.
Хотя как
сказать. Представим такую житейскую ситуацию. Садовод собрал
на своем дачном участке урожай яблок и решил похвастаться самым крупном плодом перед соседями. Будет ли он перебирать все яблоки, чтобы выбрать предмет
гордости? Конечно, нет. Самое большое яблоко никому не нужно. Нас интересует
самое большое яблоко с определенной степенью
вероятности. Кроме того, в термин «большое» мы вкладываем не вес яблока и
не его геометрические размеры, а его зрительный образ.
Пусть у нас
100 плодов. Берем первое попавшееся более-менее крупное яблоко и считаем, что оно
самое большое со степенью вероятности, намного превышающей 1% (1/100). Второе
выбранное яблоко (а оно, естественно, должно быть больше первого) существенно
повышает вероятность выбора самого большого. Так очень скоро, перебрав
(взвесив, измерив или просто оценив на глаз) всего лишь несколько яблок, а не все сто, можно выбрать относительно самое большое яблоко. Кто-то возразит, что яблоки
перед отбором могут быть кем-то
отсортированы так, что самое большое окажется в хвосте очереди (на дне
корзины). Но это уже будет искусственная ситуация, враждебная человеку[11].
Мы же говорим о дружественных
ситуациях. Данный алгоритм станет совсем естественным,
если отбирается не самое большое, а, например, самое красивое яблоко. Здесь полный перебор будет уж совсем диким. К
понятиям большое
и красивое можно приложить теорию
нечетких множеств, о которой речь пойдет в этюде 6.
К
сожалению, задачи, приведенные в данной книге, начиная с самой простой (задача
о купце и сукне – см. этюд 1) и заканчивая самой сложной (это, наверное, задача
о трехсторонней дуэли – см. этюд 6), нельзя отнести к разряду естественных. Все они довольно надуманные, призванные скорее
иллюстрировать возможности Mathcad, а не показывать пути решения практических
задач. Автора утешает и одновременно огорчает то, что таким недостатком грешат
почти все книги по программным средам. Надуманная
задача – это призма, сквозь которую вдумчивый читатель посмотрит на реальную задачу.
Пример 8. Как автор продавал программы
Эту главку этюда автор
предваряет эпиграфом, но не простым, а специфическим – маленькой программкой.
На рис. 2.9 в этюде 2 мы
решали типовую задачу линейного программирования – задачу о плане выпуска
стульев. Если цель производства – выпуск максимального количества стульев, то
их число определялось правильно: 110+40=150 стульев. Если же целевая функция –
общая цена стульев, то ответ был дробный: 18.33 стульев первого типа и 113.33
стульев второго. Как эти цифры округлять и будет ли являться
правильным решением округление дробного ответа?
Рис. 3.10. Определение плана выпуска стульев: перебор
Оказывается, при переборе
всех вариантов выпуска стульев (а их не так уж много – на рис. 3.10 мы
просчитали 150 на 150 = 22 500 вариантов) можно найти два оптимальных плана,
причем самый оптимальный и по цене, и по количеству (20+112=132 стула
стоимостью 1504 у.е.) – это
не округление дробного ответа, полученного на рис. 2.9. Возвращаясь к теме враждебности
задачи, можно так подобрать ее условия, что ответ окажется совсем вдалеке от первоначального дробного…
Это был эпиграф, приступаем
к рассказу.
У Михаила Жванецкого часто
спрашивают, откуда он берет темы для своих миниатюр. «Выглядываю в окно и прислушиваюсь
к разговорам на улице», – таков ответ великого сатирика. «А как Вы все это
запоминаете?», – следует новый вопрос. «Да я забыть не могу!»
Житейские сюжеты стоит
коллекционировать и для написания компьютерных
этюдов, что является хобби автора этой книги.
По профессии автор –
преподаватель вуза (Московского энергетического института), где он читает курс
лекций по информатике и смежным дисциплинам, а также руководит группой
технологов и программистов, разрабатывающих обучающие программы и компьютерные
тренажеры для ТЭС и АЭС[12].
Электростанциям и энергообъединениям нужны наши
программы, но их приобретению мешает пресловутый кризис неплатежей. Вот какой
компьютерный этюд имел место в марте
1997 года.
Акционерное общество Тамбовэнерго, не имея свободных денег, тем не менее изъявило желание приобрести наши программы. Котовскому
лакокрасочному заводу (ЛКЗ – Тамбовская обл.) для производства нужна
электроэнергия. Московскому энергетическому институту для ремонта аудиторий
требуется краска. Нашей научной группе необходимо новое компьютерное «железо»,
инструментальные средства и, естественно, зарплата. Для решения подобных
проблем человечество еще на заре цивилизации придумало деньги[13].
Переход же нашей страны от непонятно чего к рынку возродил натуральный обмен – бартер[14].
В вышеописанной товарной цепочке не хватало одного звена, чтобы она замкнулась.
К счастью, в МЭИ поступила партия компьютеров, парочку которых мы договорились
обменять на краску. В этой комбинации заключается только часть описываемого компьютерного
этюда, если вспомнить шахматное
толкование слова «этюд» – решение головоломки путем составления цепочки ходов.
Вторая часть компьютерного этюда имела место уже в Тамбове и в Котовске
– на ЛКЗ. В Тамбовэнерго мне (автор переходит к
рассказу от первого лица) после сдачи программ выдали доверенность на получение
лакокрасочной продукции на 14 млн., естественно, старых рублей в счет
задолженности завода за электроэнергию и отправили в Котовск.
В отделе сбыта ЛКЗ сначала наотрез отказались отпускать краску за какие-то там
непонятные задолженности, а не за живые деньги, но после угрозы отключения
света и тепла с трудом, но согласились. Краска, которая мне подходила[15],
вернее не мне, а отделу снабжения МЭИ, стоила 14 600 рублей за литр и
разливалась в тару (в барабаны, если
следовать москательному жаргону, которого я нахватался в Котовске)
объемом 15 и 55 литров. Пустые барабаны стоили 24 и 30 тыс. рублей
соответственно. Работница отдела сбыта ЛКЗ (ее звали Оля), выписывая на компьютере накладную, спросила, в каких
емкостях (пардон, барабанах) я возьму краску. Чутье давнего собирателя компьютерных этюдов сразу подсказало, что
тут кроется типичная и, главное, реальная задача линейного программирования, где целевая
функция, которую нужно максимизировать, – суммарный объем краски, переменные – количество наполненных
краской барабанов по 15 и 55 литров, которые нужно забрать, и три ограничения – (1) стоимость краски не
должна превышать оговоренных с Тамбовэнерго 14 млн.
рублей, (2) нельзя брать неполную банку (ограничение на целочисленность
переменных) и (3) количество банок разной вместимости не должно быть
отрицательными числами[16].
Оля вызвалась помочь решить эту оптимизационную
задачу и тут же с помощью калькулятора[17]
прикинула, что мне нужно взять 16 больших и 2 маленьких барабана, вмещающих 910
литров краски на сумму 13 млн. 814 тыс. рублей. Вспомнив, как я отчаянно
торговался в Тамбовэнерго и все-таки увеличил цену
программ с 12 до 14 млн. руб., я спросил у Оли, а можно ли не терять 186 тысяч
– не оставлять их Тамбовэнерго. Она сказала, что нет,
так как такие задачи решает чуть ли не каждый день,
оптимизируя не только стоимость краски, но и ее загрузку в контейнеры различной
вместимости[18], и
что она «собаку съела» на решении таких проблем.
Наблюдая за
«танцем» Олиных пальцев на кнопках калькулятора и за числами на его дисплее, я
понял, что Оля использует так называемый «рабоче-крестьянский» и, главное,
ненадежный алгоритм оптимизации: сначала выбирается краска в большой таре, а
затем остаток денег (или объема контейнера) заполняется краской в маленькой
таре. Примерно так мы пакуем чемодан, отправляясь в поездку, – сначала кладем в
него крупные вещи, а потом напихиваем в пустые пространства всякую мелочь. Еще раз вспомнив Вийона (смотри сноску 17), я спросил у Оли,
почему она не использует для решения таких задач компьютер и табличный
процессор Excel, рабочий лист которого как будто специально был выведен на
экран ее компьютера. Я тут же вызвался показать, как это делается. В среде
Excel есть так называемый Решатель (Solver),
диалоговое окно которого вызывается командой Найти решение... из меню Сервис.
В этом окне пользователь указывает ячейку, хранящую целевую функцию, значение
которой нужно максимизировать, ячейки с переменными поиска (в начале
оптимизации они либо пусты, либо хранят значения первого приближения к
максимуму) и ограничения.
Алгоритм
оптимизации с помощью Решателя Excel можно назвать «ленивым»: пользователь
формирует таблицу расчета и говорит: «По щучьему велению, по моему хотению
сделай так, чтобы»... целевая функция приняла максимальное (минимальное,
определенное) значение, но при этом были выполнены все ограничения». Для этого
пользователю достаточно нажать кнопку Выполнить.
Решатель Excel выдал нам старый результат – 16 больших и 2 маленьких барабана.
Но сдаваться не хотелось.
Есть
хорошее правило – проверять решение задачи не только другими методами, но и
другими программными средствами. Кроме того, не следует забывать о
KISS-принципе программирования. С поцелуями он ничего общего не имеет, хотя
хорошее отношение к решаемой задаче и к компьютеру в нем просматривается. KISS
– это аббревиатура английской фразы: «Keep It Simple, Stupid! – Делай это проще, дурачок!» Она
призывает решать поставленную задачу наипростейшими способами и прибегать к
изощренным алгоритмам и методикам только тогда, когда простые способы не
годятся из-за длительности времени счета или из-за нерационального
использования других ресурсов человека и/или компьютера[19].
Простейший
способ решить на компьютере поставленную задачу – это перебрать все варианты и остановиться на
оптимальном. Благо вариантов не так уж много – 1088: на отпущенные 14 миллионов
можно было взять не более 63 маленьких барабанов с краской или не более 16
больших [20].
Перебор можно назвать «компьютерно-рабоче-крестьянским»
методом решения. Но помимо прочего он может дать стопроцентную уверенность не
только в правильности, но и в единственности
найденного решения и даже показать, что таких решений несколько. А такая
ситуация нередка в задачах целочисленного
линейного программирования.
Итак,
перебор. Следуя вышеописанному правилу, новый метод решения задачи необходимо
совместить с новым программным средством для его реализации. Это, конечно,
можно было сделать и в среде Excel, составив таблицу всех решений и/или написав
программу перебора на языке Visual Basic for
Applications (VBA),
встроенном в Excel. Но у Оли на компьютере был установлен еще и Mathcad
(феномен рояля в кустах). Он довольно успешно решает задачи самого разного
плана (включая и экономические) без обращения к чистому программированию (BASIC, C, Pascal и др.). Кроме того, в то
время я работал над книгой, которую читатель держит в руках. Пример с краской эту книгу только украсит (нечаянный каламбур).
Рис. 3.11. Задача о краске
Рис. 3.11a. Задача о краске (с функцией match) (вставка 7/10/2003)
Решение задачи о краске в Интернет на Mathcad Application Server (вставка 25/12/2003)
Протокол
«контрольного взвешивания» краски в среде Mathcad приведен на рис. 3.11.
Комментарии поясняют, что происходит в формулах. Во-первых, функция Maximize, как и ожидалось, дала дробный ответ (см. пункт 2) –
маленьких банок можно не брать, если можно брать дробное количество больших.
Пришлось, вспомнив эпиграф и название этюда, перейти к перебору вариантов. В
Mathcad-документе формируются две матрицы с именами Об (пункт 3.2) и Ст (пункт
3.3), элементы которых (их 1088 – у матриц 17 столбцов и 64 строки) хранят
значения объема (Об) и
стоимости (Ст) краски в
зависимости от комбинаций расфасовки. Далее (пункт 3.4) некоторым элементам матрицы Об присваиваются нулевые
значения, если данные комбинации расфасовки не проходят по стоимости. Остальное
– ловкость рук и никакой математики: в пункте 3.5 определяется номер строки
(переменная N_15) и номер
столбца (N_55) матрицы Об, на пересечении которых
находится элемент с максимальным значением. Ответ (6 маленьких барабанов и 15
больших) неприятно удивил Олю. Она невольно обманывала меня на 5 литров краски
и на 139 тыс. руб.
Метод
поиска координат точки максимума, реализованный на рис. 3.11 (двойная сумма),
имеет существенное ограничение: в анализируемой матрице (у нас это Об) должен быть только один
максимальный элемент. Если их несколько, то ответ будет неверен: в переменные N_15 и N_55 будут
записаны суммы координат точек с
максимальным элементом. Мы это наблюдали в пункте 2 на рис 3.9.
Так Mathcad
сэкономил мне почти полторы сотни тысяч рублей. Деньги не такие уж большие, но
если присовокупить к ним новый компьютерный этюд в книгу, новую тему лекции и
новую лабораторную работу по информатике, а также гонорар за эту книгу, то игра
стоила свеч.
Вернувшись из Тамбова домой
в Москву, я в спокойной обстановке у своего родного компьютера еще раз
проанализировал задачу. И вот что получилось.
Во-первых, заставить Решатель
Excel правильно «разъяснять» задачу о краске можно было, изменив начальные
установки Решателя. А для этого нужно было не полениться и нажать на кнопку Параметры... в диалоговом окне Поиск решения. В новом диалоговом окне Параметры поиска решения достаточно
было допустимое отклонение уменьшить с 5 до 1%. После этого правильное решение
(15 больших и 6 маленьких барабанов) было бы найдено. Честно говоря, в Excel
плох не Решатель, а его начальные установки. Очень мало пользователей Excel,
прибегающих к услугам Решателя, нажимают кнопку Параметры... Тот же, кто разбирается в сути установок оптимизации,
как правило, с Excel не работает. Отсюда и недоразумения.
Во-вторых, и Оля, и Excel, и
Mathcad в разной степени меня немножко обманули[21]:
910 литров краски можно было отгрузить и другим вариантом – 13 маленьких и
столько же больших барабанов[22].
В этом случае осталось бы «сдачи» всего 12 тыс. рублей. Более того, решение
задачи о краске с новой целевой функцией (стоимость краски в банках) дает еще
один результат: 37 маленьких и 6 больших барабанов, выбирающий еще одну тысячу
из Тамбовэнерго.
|
Вариант
расфасовки (число маленьких барабанов/число больших барабанов) |
2/16 |
6/15 |
13/13 |
37/6 |
|
Объем
краски (л) |
910 |
915 |
910 |
885 |
|
Остаток
невыбранных денег (руб.) |
186 000 |
47 000 |
12 000 |
11 000 |
В-третьих,
когда я показал эту таблицу в отделе снабжения МЭИ, то мне было сказано, что
самый оптимальный вариант и для меня (мне важны деньги) и для МЭИ (ему нужна
краска) четвертый: у Тамбовэнерго были бы выбраны
почти все деньги, а 885 литров краски, как это ни кажется странным, больше, чем
910 и 915. Дело в том, что при крупной расфасовке много краски теряется
из-за переливов в меньшую тару. 15-литровый барабан можно взять в ремонтируемую аудиторию и там полностью использовать.
Неверное решение задачи
получается не только из-за плохих методик или дефектных программных средств, но
и из-за того, что пользователь сам толком не знает, чего он хочет. Все
программы решения задачи линейного программирования требуют четкого
формулирования одной единственной целевой функции[23].
При решении учебных задач цель ясна. А что является целью в жизни? Но это уже
не математика, а философия...
У метода перебора,
реализованного на рис. 3.11, есть три собственных ограничения:
1) число
переменных не может быть больше двух, так как в среде Mathcad есть векторы и
матрицы, но нет тензоров (трех- и более мерных матриц);
2) при
чрезмерном размере матрицы компьютер отказывается иметь с ней дело, выдавая
протестующее сообщение типа «не хватает
памяти»;
3)
счет (если перебор можно назвать счетом) может длиться нестерпимо долго.
Первые два ограничения
снимаются при переходе от метода формирования матрицы (рис. 3.11) к методу перебора
вариантов с запоминанием только оптимального плана, который можно реализовать
средствами программирования, что мы и сделаем в этюде 6 (см. рис. 6.31 и 6.32).
Метод перебора оказывается незаменимым (то есть опять же бывает не таким уж
извращенным), когда задача, оставаясь целочисленной, теряет свою линейность[24].
В этом случае традиционные методы (например, симплекс-метод) часто оказываются
бессильными.
Тем не менее
реализация метода перебора в среде Mathcad всегда будет извращением чистой
воды. Mathcad – это программа интерпретирующего
типа с низкой скоростью выполнения исходного текста. Для перебора нужны не
просто компиляторы, а компиляторы, оптимизирующие время выполнения
программы.
Пример 9. Опять задача старушки «Наири»
Чтобы как-то оправдать метод
перебора, вернее, оправдать самого автора книги, ухватившегося за него,
вернемся к рис. 3.3 и 3.4. Анализируя тестовые
функции, прощупывая их и так и сяк вблизи точки минимума (поверхность, линии
уровня), мы согрешили перебором, но
никак не воспользовались плодами этого греха. Исправим ошибку.
Рис. 3.12. Поиск места для ларька
На рис. 3.12 помещен протокол решения задачи о
поиске места для ларька на дачном участке. Критерий поиска – минимум суммы
расстояний от ларька до всех остальных домиков. Их координаты X и Y – случайные
числа в интервале от 0 до 20 (наша задача учебная). Ларек может быть либо встроен в один из домиков (пункт 1),
либо стоять отдельно (пункт 2). На рис. 3.12 координаты встроенного ларька
определяются перебором. Затем эти координаты (Xiопт и Yiопт)
становятся первым приближением для уточнения местоположения отдельно стоящего
ларька. Заканчивается расчет графическим описанием и сути и решения задачи.
Здесь главное – правильно отформатировать точки на графике. Поэтому выведено
окно форматирования графика.
Задача коммивояжера и ее решение в среде Mathcad (функция anneal из e-book «Численные методы - вставка 10/07/2003))
Вернемся к
тестовым задачам на рис. 3.3-3.5.
На рис. 3.3 и 3.4
формируются матрицы М, элементы
которых – значения анализируемых функций в узлах сетки, накрывающей точку
минимума. Элементы матрицы М средствами Mathcad превращаются в линии уровня и в
поверхность. Но эти матрицы могут сослужить нам и другую службу – координаты их
минимальных элементов могут стать точками первого приближения к минимуму.
Нащупать минимум (максимум) функции более чем двух аргументов (например,
функции Пауэла – см. рис. 3.5) можно средствами
программирования (см. этюд 6).
Транспортная задача,
решенная нами на рис. 2.10, кочует из одного учебника в другой. Везде отмечается
такой ее парадокс – по самому дешевому маршруту при минимизации затрат на
перевозки ничего не возится. Если бы мы решали эту задачу вручную без
компьютера, то сначала полностью загрузили бы дешевый маршрут, а потом все
остальные. Этим парадоксом может воспользоваться хозяин транспортного
предприятия, максимизировав свою прибыль от перевозок (см. рис. 3.13):
Рис. 3.13. Транспортная задача (извращенное решение)
В этом случае второй по дороговизне маршрут (1200 у.е.) остается свободным – внешне все выглядит прилично.
Но парадокс
задачи не в этом. Вернее, не только в этом. Дело в том, что она недостойна не
только функций Minimize и Maximize, но даже и
грубого перебора, так как сводится к решению простейшего уравнения:
с1м1+с2м1=40
Если с1м1=0, то с2м1=40, и затраты
на перевозки максимальны. Если с2м1=0, то с1м1=40, и затраты
максимальны. Рис. 2.10 и 3.13 – это чистой воды извращения. Или неумение либо нежелание
подумать как следует над задачей.
Пример 10. Mathcad и
булевы (логические) функции[25]
(English version of text)
В наборе
встроенных Mathcad-функций и операторов (см. приложение 2 и 3) нет булевых (логических)
функций (Not, And, Or и т.д.),
присутствующих во всех языках программирования. А без этих функций не обойтись
при решении разного рода логических задач (см., например, задачу о
трехсторонней дуэли на рис. 6.36-6.40 в этюде 6), при организации циклов и
ветвлений в программах (см. этюд 6) и т.д. Как тут быть и почему разработчики
Mathcad не встроили в него эти довольно-таки простые, но такие необходимые
функции? Это тем более выглядит странным, если принять во внимание тот факт,
что вся цифровая вычислительная
техника, на которой, кстати, работает и сам Mathcad, хранит только нули и
единицы, а все арифметические и прочие действия – это чистой воды операции
булевой алгебры над этими нулями и единицами.
Давайте в
этом разберемся.
Рис. 3.14. Логические операторы и
функции
Во-первых,
булевы функции в среде Mathcad можно определить.
Математика (см., например, «Справочник по математике для научных работников и
инженеров» Корн Г. и Корн Т.) оперирует одной
одноместной (с одним аргументом) и семью
двухместными (с двумя аргументами) булевыми функциями. Все они определены в
пунктах 0-7 на рис. 3.14. Если булеву переменную уподобить выключателю с двумя
позициями («вкл» и «выкл»),
то конъюнкция – это последовательное
соединение выключателей (пункт), а дизъюнкция
– параллельное. Электрический аналог эквиваленции (пункт 3) может очень пригодиться для освещения
длинного коридора, свет в котором зажигается и тушится независимо в двух его
концах двумя выключателями.
В пункте 8
на рис. 3.14 сформирована трехместная булева функция с именем Решение,
возвращающая вердикт жюри из трех человек: решение проходит, когда «за»
голосуют двое или трое. Воздерживаться или уклоняться от голосования нельзя.
Функция Решение
(программная реализация процедуры голосования) в пункте 8 на рис. 3.14 также
имеет электрический аналог (аппаратная реализация – машинка для голосования) –
комбинацию выключателей, соединенных последовательно и параллельно.
Двухместные
булевы функции (пункты 1-7 на рис 3.14) имеют четыре (22) комбинации
значений аргументов (таблица истинности), трехместные – уже 8 (23),
одноместная, естественно, только две (21) – 0 или 1. Самих же
двухместных булевых функций может быть 16 (42 – мы описали только
семь), трехместных уже 64 (43 – мы описали только одну). Одноместных
булевых функций четыре (41 – мы описали только одну). Вот другие три
одноместные булевы «функции» y2(x):=1, y3(x):=0 и y4(x):=x. Но никакой практической ценности
в программировании они не имеют: первые две (y2 и y3) – это константы, а y4 – это просто
сам аргумент. Ненаписанные нами остальные девять (16-7) двухместные булевы
функции (там тоже есть константы) имен не имеют и, как правило, ни в
математике, ни в программировании не применяются.
В математике булева функция выдает два значения (0 –
1, да – нет, истина – ложь и т.д.), в программировании же – минимум три:
да, нет и... аварийный останов, связанный с ошибкой (один или несколько
аргументов не определены). Такую ошибку можно обработать (в Mathcad для этого
служит оператор on
error) и пустить расчет по третьему пути. Одноместных
булевых функций может быть больше четырех. Как понравится такая функция: y5(x):=if(rnd(1)>0.7, 1, 0),
возвращающая единицу с вероятностью 30%, и нуль – с вероятностью 30%.
Функцию Решение можно
построить намного проще – вычислить среднее арифметическое значений аргументов.
Эту работу выполняет встроенная Mathcad-функция mean. Если оно
окажется больше, чем 0.5 – то решение принято (возвращается единица), нет –
нуль:
Решение(V):= mean(V) > 0.5
Число
аргументов новой функции Решение, таким
образом, допустимо увеличивать, не прибегая к сложному дереву булевых операций,
показанных в пункте 8 на рис. 3.14.
В пункте 9
на рис. 3.14 формируется еще одна функция Решение для голосования комитета с любым числом членов,
принимающих решение большинством голосов. Но при этом часть голосующих обладает
правом вето (пример – Совет
Безопасности ООН где, как писал Джорж Оруэл: «все равны, но
некоторые равнее»). Люди (или страны: США, Россия,
Китай, Франция и Великобритания, если иметь в виду СБ
ООН) с правом вето у нас объединены в вектор Const (постоянные члены СБ), а все остальные – в вектор Var. Если для
принятия решения большинством голосов годится среднее арифметическое, то для
блокировки принятия решения – среднее геометрическое (gmean): корень n-й степени из
произведения n сомножителей. Эта встроенная функция появилась только
в восьмой версии Mathcad. При этом gmean требует, чтобы все элементы вектора (матрицы)
аргумента были ненулевыми. Поэтому в пункте 9 на рис. 3.14 мы сначала переопределили
функцию gmean так, чтобы
она «проглатывала» и нулевые элементы вектора-аргумента, а потом уже с ее
помощью сформулировали функцию Решение для электората типа СБ ООН. В
конце пункта 9 показаны три типичных исхода голосования:
—
решение принимается большинством голосов;
—
решение проваливается одним человеком с правом вето;
—
решение не проходит, так как большинство против.
Конечно,
использование среднего геометрического для подсчета голосов – это чистой воды извращение (см. название данного этюда).
Тут можно использовать функцию And – просто логическое умножение безо всякого корня. В
пункте 10 на рис. 3.14 сформулированы функции And и Or, аргументы
которых – векторы-столбцы с переменным числом элементов[26].
Этой главке автор хотел дать
и другое название – «Казнить нельзя помиловать». Но уж
больно оно избитое. Традиционно читателя просят поставить запятую в этом
предложении[27] и
проследить, как меняется смысл вердикта в зависимости от места такого невинного
знака препинания.
А как вам понравится такой
ответ на вопрос о месте запятой: запятую нужно «размазать» по предложению – n процентов запятой поставить после слова «казнить», а 100-n
– после слова «нельзя». Трактовать такую новую грамматическую (пунктуалистическую?) конструкцию можно по-разному. Но
сначала поговорим о самой постановке вопроса.
Один лидер
«третьего рейха» любил повторять, что он всегда хватается за пистолет, слыша
слово «культура». Сталкиваясь с логической
задачей, программисты «хватаются» за троицу булевых функции Not,
And, Or и т.д. Но их-то
и нет в списке встроенных функций
Mathcad. Нет там и булевых (логических) переменных. Тут программист чертыхнется
(а зря – см. ниже) и напишет соответствующие пользовательские функции (см. пункты 0 – 7 на рис. 3.14), заставляя
числовые[28]
переменные выполнять по совместительству и роль булевых. После этого ничего не стоит написать булеву функцию Решение,
возвращающую единицу (логическое
«Да») или нуль («Нет») в зависимости
от итогов голосования – решение принимается, если двое или трое присяжных
проголосуют «За».
Возвращаясь
к дилемме «казнить-помиловать» и допуская совмещение должностей присяжного,
судьи и палача, можно попытаться заменить в схеме пункта 8 электрическую
лампочку на... электрический стул. Говорят, что подобная схема рубильников на
самом деле запитывает американское орудие казни.
Каждый из трех, приводящих приговор в исполнение, надеется, что он включил не
настоящий рубильник, а муляж рубильника.
Еще немного
об «электрических цепях». Последнее время в быту получают распространение
выключатели, плавно меняющие накал
лампочек от нуля до ста процентов. Еще раньше такие устройства (реостаты) стали
применяться в театрах и кинозалах. Медики уверяют, что плавный переход от света
к темноте через полумрак благотворно влияет на зрение.
А можно ли
подобными регуляторами заменить выключатели в вышеприведенной схеме аппаратной
реализации процедуры голосования? Может ли функция Решение иметь не
только логические, но и вещественные аргументы и возвращать вещественное значение, плавно меняющееся
от нуля до единицы (от 0 до 100%)? Очень часто, осуждая или оправдывая
кого-либо, трудно прийти к однозначному решению. Даже на первый взгляд явное
преступление может иметь такую оценку – «это скорее беда, чем вина подсудимого».
Но людей, принимающих решения, по-прежнему заставляют давать только черно-белые
оценки[29].
Толерантность[30]
сначала проникла в религию.
Человечество, нахлебавшись крови в религиозных войнах[31],
относительно поумнело. Сейчас цивилизованный человек может сказать о себе, что
он на k процентов
атеист, на l процентов
мусульманин, на m процентов – католик, а на n процентов
– протестант (гугенот – вспомним Варфоломеевскую ночь и Париж, который стоил
мессы). И не обязательно, чтобы k+l+n+m равнялось ста процентам. Во многих церквях Америки по
пятницам служит мулла, по субботам – раввин, а по воскресеньям – священник
(поп, пастор, ксендз) и никого это не шокирует. Затем толерантность охватила
мир искусства, размыв систему
классических канонов и стилей. Сейчас главное – это талант художника и то, что
он хочет сказать миру. И не важно, кто он – реалист, импрессионист (нео-, пост- и т.д.) или просто
примитивист, впервые взявшийся за кисть в 70 лет. Теперь стали говорить и о
терпимости в науке. Ее проявления –
теория нечетких множеств (fuzzy sets – см. рис. 6.41-6.45 в этюде 6) и теория нечеткой логики (fuzzy logic). Неоднозначность оценок стала превалировать не только в
гуманитарных дисциплинах (см. сноску 27 с деликатной подсказкой Word’а), но и в точных науках – в математике, например. Автор где намеренно, а где по незнанию (по недопониманию – хороший пример нечеткого
множества в живом языке) не совсем верно трактует положения теории нечетких
множеств. Раньше бы такого автора с кашей съели. А теперь ничего – публикуют,
читают.
Но это,
конечно, не значит, что размываются все грани черно-белых оценок. Об этом
хорошо сказано у Пушкина:
Ах! Чувствую: ничто не может нас
Среди мирских печалей успокоить;
Ничто, ничто… едина разве совесть.
Так здравая она восторжествует
Над злобою, над темной клеветою. –
Но если в ней единое пятно,
Единое, случайно завелося,
Тогда – беда! Как язвой моровой
Душа сгорит, нальется сердце ядом,
Как молотком стучит в ушах упрек,
И все тошнит, и голова кружится,
И мальчики кровавые в глазах…
С другой
стороны у Ф.М.Достоевского в «Скверном анекдоте» читаем: «Был он и честен, то
есть ему не пришлось сделать чего-нибудь особенно бесчестного…».
Давайте
посмотрим, как нашу задачу о голосовании можно решить с учетом положений теории
нечеткой логики (пункт 10 на рис. 3.14). Задачу можно обогатить элементами нелинейности, приняв во внимание
условное деление голосующих на консерваторов
(k), традиционно склонных к осуждающим приговорам, центристов (c) и либералов (l – эль). Степень радикальности жюри присяжных (парламента и вообще любого электората)
будем учитывать через коэффициент k.
Голосующие устанавливают степень своего решения «за» (от 0 до 1), но на исход
голосования влияют функции yk, yc
и yl, демпфирующие крайние оценки (см. пункт 10.1).
«Цветная»
функция Решение,
построенная на функциях min и max (см. пункт 10.2), при логических значениях аргументов
(0 или 1) полностью эквивалентна своему «черно-белому» аналогу, использующему
функции And и Or (см. пункт 8). Встроенные функции min и max
способны работать и с логическими, и с вещественными, и даже с комплексными[32]
аргументами. Кроме того, функции min и max удобны еще
и тем, что их аргументами может быть вектор-столбец (аргумент функции max в пункте 10.2),
вектор-строка (min) и даже матрица (см. рис. 6.34 в этюде 6). Это
позволяет комбинировать типы аргументов (горизонталь-вертикаль) создаваемой
«цветной» логической функции, делая ее более компактной и более легкой для
понимания. (Здесь вызывается не функция, а постфиксный оператор – это позволяет
убрать лишние скобки.)
Ладно,
скажет читатель, а что делать с вердиктом присяжных такого рода: «Виновен на
57%, невиновен на 43%»? Что делать? Смотреть на графики, материализующие
«цветное» решение!
В пункте
10.2 на рис. 3.14 визуализированы вердикты присяжных при фиксированном решении
либерала 0.5 (воздержался – ни то ни се).
Интерпретация цвета участков поверхности решения (здесь, к сожалению, не цвета, а оттенки серого) может быть такая:
·
красный цвет графика говорит сам за себя – кровь,
«вышка»;
·
оранжевый –
пожизненное заключение;
·
желтый – каторга;
·
зеленый – тюремное заключение;
·
голубой – условное осуждение;
·
синий –
общественное порицание;
·
фиолетовый – невинен.
Цветовую палитру («Каждый охотник желает знать, где сидят фазаны!») можно сдвигать, учитывая тенденции в общественном сознании и изменения в законодательстве – мораторий на смертную казнь, например. При этом нужно будет «сдвигать вниз» (в холодные тона) и другие виды наказаний. В наших тюрьмах условия содержания такие, что смертная казнь может оказаться просто наградой. Основной довод противников смертной казни в том, что жизнь – это Дар Божий, и только всевышний может приговорить к высшей мере. Но и свобода не меньший дар! Второй довод в том, что смертная казнь делает невозможным исправление судебных ошибок. Но. Отсидел человек 20 лет в камере пожизненного заключения, а ему говорят, пардон, мы ошиблись. Кто вернет загубленную жизнь.
Строить
«цветные» логические схемы поможет и нечеткая функция Not:
Not(x):=½1-x½ или ½100-x½.
В пункте
10.3 на рис. 3.14 функции max и min заменены на их «аналоги» – на функции mean
(среднее арифметическое) и gmean (среднее
геометрическое). Поверхность стала более гладкой – природа, как мы знаем, не
терпит острых углов.
В пункте 11
на рис. 3.14 сформированы многомерные функции And и Oг. Но записать допустимо еще проще:
And(x):=min(x) Or(x):=max(x),
А можно
работать только с min и max, которые
хорошо справляются и с булевыми (четкая логика), и с вещественными (нечеткая
логика) аргументами. Но если пользователь оптимизирует программу (см. главку
6.12), то вместо функции min лучше использовать оператор
умножения. Дело в том, что при умножении сразу возвращается нуль, если первый
сомножитель нулевой. Функция же min излишне педантична – она
перебирает все элементы своего аргумента-матрицы (вектора).
Но увлекаться
статистическими функциями (min, max, mean, gmean, rnd, var
и др.) при реализации логических схем нужно осторожно. Уинстон Черчиль говорил, что есть
Большая Ложь, Просто Ложь и… Статистика – героиня этого этюда.
Три дивертисмента
1. Дивертисмент политический.
Наши политики, обсуждая статус Чечни (Страны Басков, Корсики и др.) загоняют себя в угол. Мол, независимость – это как беременность: она либо есть, либо ее нет. Нельзя быть чуть-чуть беременной, нельзя быть чуть-чуть независимой и т.д. и т.п.
Это противоречие можно
разрешить с помощью теории нечетких
множеств. Рассказ о ее основах обычно начинают с парадокса кучи зерна. Сто зерен – это куча или нет? Конечно, нет, – это скорее горсть зерна. А если к этой горсти прибавить еще одно зерно, станет
ли она кучей? Опять нет. А если еще зерно и еще зерно. Рано или поздно мы
получим кучу. Люди пытались с позиций классической математики определить точное
число зерен, разграничивающее горсть и кучу, но ничего путного из этого не
получалось. Примерно так сейчас политики пытаются найти количество признаков (полномочий), отделяющих независимое государство от субъекта
федерации. Все бы ничего, да кровь льется.
Дело в том, что понятие
«независимое государство» традиционно (исторически) рассматривается как элемент
четкого множества. Дескать,
государственное образование может либо принадлежать, либо не принадлежать к
этому множеству.
Но все намного сложнее и
намного проще. Понятие горсть и куча – это нечеткие
множества. Сто зерен – это одновременно и горсть и куча. При этом значение
функции принадлежности ста зерен к множеству горсть равна почти единице,
а к множеству куча – почти нулю. Если к этой сотне добавить
зернышко, то первое значение (близкое к единице) чуть-чуть уменьшится, а второе
(близкое к нулю) – чуть-чуть увеличится. Опять повторяем – природа не терпит
острых углов и черно-белых оценок.
Проблема кучи зерна решается
с позиции теории нечетких множеств так: насыпаются разные количества зерен, а
люди (эксперты; лица, принимающие решения) дают такие
оценки: «это горсть (0)», «это скорее горсть, чем куча (0.33)», «это скорее
куча, чем горсть (0.67)», это и не горсть и не куча, а что-то среднее (0.5),
«это куча (1)» и т.д. (так сейчас, к примеру, проводят опрос общественного
мнения). После этого строится функция
принадлежности (см. главку в этюде 6) к нечеткому множеству «куча зерна».
График этой функции – плавная и пушистая кривая, поднимающаяся от нуля
(мало зерен) к единице (много зерен) без каких-либо скачков. Функция
принадлежности к множеству «горсть зерна» имеет «горбатый» график: нули по
краям (идем от отдельных зерен к куче) и единица посредине (горсть зерна).
Проблема Чечни – это
проблема не только России, но и всего мирового сообщества в том плане, что в
уставе ООН заложены два взаимоисключающих принципа – принцип нерушимости границ и право нации на самоопределение (на
независимость). Решить эту проблему можно, приняв во внимание, что понятия «нация» и «независимое государство»
– это также нечеткие множества. Государственное образование (область, район,
республика) может быть и чуть-чуть независимым и совсем независимым. Читатель
может сам при желании составить такую таблицу: в первой колонке написать
названия стран (включая субъекты Российской Федерации), а во второй – значение функции
принадлежности этих стран к множеству «независимое государство». Германия
независимое государство или нет!? Вроде бы да, но многие ее суверенные
полномочия ограничены членством в НАТО, в Европейском Союзе, в Общем рынке и т.д. Такой важный атрибут независимости, как
национальная валюта, и та скоро у Германии пропадет (евро!). Немецкий язык все
больше становится неким местным диалектом – все серьезные научные конференции
проводятся на английском языке. Так что «независимости» у этой страны сейчас намного
меньше, чем у той же Чечни. Говоря языком теории нечетких множеств, можно
сказать, что значение функции принадлежности к множеству «независимые
государства» у Германии ниже, чем у Чечни. То, что в Бонне много посольств
иностранных государств, а в Грозном пока ни одного, ни о чем не говорит.
Представим себе, что завтра все страны порвут с Германией дипломатические
отношения. От этого статус Германии как независимого государства только
повысится. На нашей планете самые независимые – это самые
одиозные государства: «алкоголики» (поставщики наркотиков), «тунеядцы» (страны,
живущие за счет помощи мирового сообщества), «хулиганы» (Ливия, Ирак, Северная
Корея – маленькие «хулиганы», Россия, США, Китай – взрослые «хулиганы»).
«Алкоголиков» и «тунеядцев» называть не будем – где
здесь вина, а где беда этих стран? «Казнить нельзя
помиловать!»
Итак, будем считать, это все субъекты Российской Федерации – независимые государства, но значения функции принадлежности у них к этому нечеткому множеству разные: у Тверской области одно, у Татарстана – другое, а у Чечни третье, самое высокое. В процессе государственного строительства эти числа могут меняться плавно (реформы) либо скачками (революции, войны, но лучше – референдумы), но никогда они не упадут до нуля и не поднимутся до единицы.
2. Дивертисмент политико-компьютерный.
Теории нечетких множеств и нечеткой логики можно приложить и к проблеме компьютерного пиратства. Закон делит всех людей на два четких множества: «множество легальных пользователей программ» и «множество нелегальных пользователей (пиратов)». В реальной жизни все намного сложней: нечетких множеств людей, причастных к компьютерам, великое множество (извините за тавтологию). Есть множество торгующих на «Горбушке» «черными» дисками и есть множество тех, кто принципиально работает только с легальными копиями и никогда не подаст руки согрешившим – нарушившим какое-либо лицензионное соглашение. Можно осью «грешник-праведник» построить горбатые статистические кривые, описывающие состояние компьютерного рынка в конкретной стране. Где находится максимум этой кривой, куда и с какой скоростью он перемещается во времени?
3. Дивертисмент компьютерный.
Даниил Хармс[33] подметил, что память – это очень странная штука: иногда запомнишь одно, а вспомнишь потом совсем другое. А бывает и так, что запомнишь настолько крепко, что потом ни за что не вспомнишь.
Основное отличие памяти человека от «памяти» компьютера в том, что человек разную информацию запоминает по-разному. Одно дело запомнить телефон случайного знакомого, а другое дело такую информацию: «Еще раз сунешь сюда нос – голову оторву!»
Элементарные ячейки памяти цифрового компьютера хранят либо нули, либо единицы, не делая никаких различий по важности информации. «Бит» информации в мозге человека – это нейронная связь различной «толщины», меняющейся, условно говоря, от нуля до единицы. Может быть, стоит заряжать конденсаторы компьютера не ступенькой, а плавно…
Семь
дивертисментов к трем дивертисментам.
А вот еще примеры того, что в жизни нет чистых нулей и единиц – нет четких и однозначных ответов на, казалось бы, самые простые вопросы.
1. Считается, что костры в лесу увеличивают опасность пожаров. Но! Туристы, собирающие для костров хворост и сухостой, культурно сжигают горючий материал, готовый вспыхнуть от удара молнии или от неосторожно брошенной сигареты. Так что костры в лесу не губят (не только губят),а защищают лес от пожара.
2. Российские политики из кожи лезут вон, добиваясь, чтобы транзитные нефтепроводы из района Каспия проходили исключительно через российскую территорию. Считается, что обходные пути перекачки нефти лишат Россию огромных доходов и политического влияния. Но! Влиять на кого-то шантажом перекрытия задвижки крайне аморально. Экономический же эффект транзита нефти может быть подсчитан только после оценки ущерба, наносимого России разрывами трубопроводов и другими авариями. Мы должны всеми правдами и неправдами добиваться прокладки трубопроводов минуя российскую территорию. Новые трубопроводы нужно прокладывать лишь после того, когда уровень эксплуатации существующих трубопроводов станет приемлемой. Это касается и газопроводов – вспомним, как под Уфой в огне сгорели два пассажирских поезда. В нормальной стране после такой катастрофы любой Газпром разорился бы, выплачивая страховки. А у нас ничего…
3. В настоящее время в мире ведется кампания по тотальному запрещению противопехотных мин. Символ этой кампании – безногий ребенок на костылях, подорвавшийся на мине, оставшейся от давнего конфликта. Но! Если бы в свое время конфликтующие стороны (например, представители народностей тутси и хуту в Бурунди) не отделили бы друг от друга минными полями, проходы в которых контролировали нейтральные силы (войска ООН, например), то жертв, в том числе и среди женщин, стариков и детей, могло бы быть намного больше. Плохи не противопехотные мины, а люди, забывающие или не умеющие ликвидировать их после окончания конфликта.
4. Расхожий лозунг ура-патриотов: «Если народ не хочет кормить свою армию, то он будет кормить чужую». Мы вскармливали Советскую армию, которая стреляла в мирных людей в Новочеркасске, с позором выходила из Венгрии, Чехословакии, Германии, Афганистана, Чечни... Красную Армию немецкие войска в 1941 году разбили за пару месяцев, а Победу добывал уж сам народ-кормилец (с помощью Мороза-воеводы): инженеры, учителя и прочий рабочий люд на целые четыре года оставили свой мирный труд и взялись за оружие. Про армию трудно судить, но вот отечественную милицию, а тем более ГАИ (ГИБДД) стоило бы поменять на импортную, некоррумпированную (на немецкую, например). Эффективнее и, что интересно, дешевле бы вышло. Армию же вообще не стоит содержать – ни свою, ни чужую. Ракетно-ядерные силы сдерживания – это по своей сути никакая не армия, а научно-техническая отрасль, работникам которой зачем-то погоны прицепили.
5. Оружие у населения у нас считают одним из главных факторов роста преступности. Но! Демократия вместе с порядком (Законом) воцарилась в Западной Европе лишь после того, как крестьяне взяли в руки оружие и стали защищать себя от средневекового рэкета – от произвола синьора. Сможет ли современная «аристократия» («братки[34]», «крыша») обкладывать поборами современных «крестьян» (предпринимателей), зная, что вместо денег можно получить пулю в лоб – и все будет законно. В стране не было бы никакого 37 года, если бы хозяева «черных воронков» (НКВДАПО) боялись хотя бы вооруженного сопротивления арестовываемых.
6. Сейчас ни у кого не поворачивается язык сказать ничего, кроме слов осуждения, в адрес террористов. При этом специально ставят на одну доску людей, захватывающих невинных жертв, и людей, вынужденных браться за оружие для решения своих политических и иных проблем (см. выше). С первыми все более-менее ясно, их нужно рассматривать как некое стихийное бедствие, от которого никто не застрахован. Нужно только стараться под него не попадать, а если попал, то правильно себя вести. Со вторым же типом «террористов» не все так просто. К ним можно отнести принцип «на то щука в море, чтобы карась не дремал». Говорят, что можно устранить любого политического деятеля – все дело в средствах, которые на это можно ассигновать (инвестировать). Того или иного лидера не устраняют не только потому, что у него сильная охрана, но и потому, что это никому пока не нужно. Или нет средств на это. Политический деятель ведет себя прилично, боясь в том числе и пули своих оппонентов (своего народа).
7. Целостность России наши политики возводят в ранг некоего идола, которому нужно приносить огромные жертвы. Но! Все дело в том, что настоящие люди чувствуют себя не только россиянами, но и европейцами, гражданами Мира. Национализм, как верно подмечено, – это последнее прибежище негодяев. Многие русские люди отделились бы от Москвы и присоединились бы, например, к Страсбургу, но не имеют на то сил, а, главное, повода. Уезжать из этой страны? Нет, спасибо! Пусть лучше уезжают те, от кого нам хочется отделиться…
Мысли, конечно, очень спорные и где-то даже извращенные, но… еще раз взглянем на название этюда…
3.3. Взгляд
эстета
После
выстрела и команды «Искать!» собака может вернуться к охотнику с тремя результатами:
1.
Собака приносит подстреленную дичь.
2.
Собака, израсходовав отпущенный лимит времени или
услышав призывный сигнал охотника, возвращается с пустыми руками, пардон,
зубами.
3.
Охотник получает «трофей» – стреляный пыж или рваный башмак,
но собачьи глаза и собачий хвост выдают собачью хитрость.
Есть
особый род эстетов, получающих
удовольствие от попыток облагораживания технического текста цитатами из
художественной литературы. Но не этот смысл слова «эстет» подчеркнут в названии
этюда. Автору уже не раз доводилось признаваться своим читателям, что для него
в программной среде важны не только чисто технические параметры
(быстродействие, богатство встроенных функций и т.д.), но и «красота»
программы. Под красотой же следует понимать не только цветовую палитру или
изящество окон и иконок, но и то наслаждение, которое программа может
доставлять при решении даже простейших задач. И не только своими новыми, ранее
неведомыми возможностями, но и своими... ошибками. Автор попытался
было описать всю эту гамму чувств, но его опередил Карел Чапек своим рассказом
«Игла», где необыкновенно точно передан дух расчетов – и не важно, проводятся
ли они на бумаге или на компьютере. Помимо этого, чапековский
отрывок поможет понять, при чем тут охотник:
Когда я работал в бухгалтерии и составлял, бывало,
полугодовой отчет, подчас случалось, что цифры не сходятся. Однажды в
наличности не хватило трех геллеров. Конечно, я мог просто положить в кассу эти
три геллера, но это была бы неправильная игра. С бухгалтерской точки зрения это
было бы неспортивно. Надо найти, в каком счете допущена ошибка, а счетов у нас
было четырнадцать тысяч. И скажу вам, когда я брался за баланс, мне всегда
хотелось, чтобы там обнаружилась какая-нибудь ошибка. Тогда я, бывало, оставался
на службе хоть на всю ночь. Положу перед собой кучу бухгалтерских книг и берусь
за дело. И для меня колонки цифр становились не цифрами, они преображались
просто необыкновенно. То мне казалось, что я карабкаюсь по этим колонкам вверх,
словно на крутую скалу, то я спускаюсь по ним, как по лестнице[35],
в глубокую шахту. Иногда я чувствовал себя охотником, который продирается сквозь чащу цифр, чтобы изловить пугливого и
редкого зверя – эти самые три геллера. И до того мне в такие минуты становилось
хорошо от этого ощущения движения и силы, такое я чувствовал вокруг себя
волнующее приволье, словно и в самом деле переживал необыкновенное приключение.
Целыми ночами я мог охотиться за тремя геллерами, и когда находил их, то даже
не думал, что это лишь жалкие гроши. Это была добыча, и я шел спать,
торжествующий и счастливый...
Поиск
решения с помощью функций root, Find, MinErr, Minimize и Maximize во многом
напоминает ружейную охоту. Пользователь формирует анализируемую функцию, вводит
ограничения, выставляет параметры поиска (заряжает ружье, выслеживает дичь), а
затем нажимает клавишу F9 (спусковой крючок ружья). Собака (cреда Mathcad) прыгает в воду и возвращается с тремя
результатами:
1.
Решение найдено (см. пункт 4 рис. 3.1).
2.
Решение не найдено (пункт 5).
3.
Mathcad пытается подсунуть пользователю то, что только
издали напоминает правильный результат (пункт 6).
При
этом ситуация осложняется еще и тем, что пользователь Mathcad, в отличие от
охотника, который знает, что такое дичь, часто не имеет понятия о том, что
такое правильный результат. У среды Mathcad, к сожалению, нет глаз и хвоста, по
которым можно определить, что именно принесено к ногам охотника – пользователя
пакета.
Работа с функциями root, Find, MinErr, Minimize и Maximize – это
хождение на охоту с чужой собакой, повадки которой неизвестны. «Своя собака» –
это методы и алгоритмы, написанные на языке Mathcad и вставленные в документ,
по которым решение ищется не вслепую, а наверняка (см. этюд 6). А если писать
программы недосуг, то вот семь советов по работе с функциями root, Find, MinErr, Minimize и Maximize:
1.
Найдя решение, еще раз заставьте Mathcad найти его уже
от новой опорной точки. Неплохо при этом использовать одновременно все
инструменты, заложенные в Mathcad. Из этюдов 2 и 3 мы знаем, что максимум,
например, можно искать минимум тремя способами (нечаянный каламбур!): через
поиск корней системы уравнений, составленных из частных производных
анализируемой функции, с помощью функции MinErr и прямым
способом – через функцию Maximize. Что здесь
сработает – неизвестно, наверное, даже разработчикам
Mathcad. Если из разных опорных точек разными методами найден один и тот же
результат, то надо перекреститься и сказать: «Слава Богу! Задача решена!»
2.
Перед решением оптимизационной задачи с ограничениями
прогоните ее не с функцией MinErr, Minimize или Maximize, а с
функцией Find для того,
чтобы оценить область существования решений.
3.
Начинайте поиск оптимального решения от одной из
точек, найденных в пункте 2 и лежащих недалеко от оптимума.
4.
Вводите ограничения постепенно: ввели первое – нашли
какое-то подобие решения, ввели второе – уточнили его и т.д.
5.
Начинайте решение оптимизационной задачи с
целочисленными аргументами без ограничений на целочисленность.
Нецелочисленный ответ всегда будет полезен, так как 1) от него можно начать
поиск целочисленного решения, 2) можно удовлетвориться нецелочисленным решением
(появление совместителя, например, в задаче об оптимальном штатном расписании)
и 3) числа можно округлить вручную, если целочисленное решение отыскать
невозможно.
6.
Проверяйте правильность найденных корней, минимумов и
максимумов построением графиков и поверхностей, где эти точки видны, благо
пакет Mathcad имеет богатый набор графики. Если аргументов у функции больше
двух, постройте графики сечений через точку оптимума (рис. 3.5) по всем
координатам и убедитесь, что там все частные производные равны нулю. Неплохо
тут протабулировать анализируемую функцию вокруг
найденной точки и показать, что отход от оптимума ухудшает результат.
7.
Прежде чем решать задачу численно, проанализируйте ее
средствами символьной математики (этюд 7). Если даже аналитическое решение не
будет найдено, то можно, например, выведенную частную производную использовать
в численном решении системы (гибридность решения
задачи – см. раздел 7.5).