Этюд 4.
Рагу из среднестатистического зайца
Рис. 4.1. Ввод и сортировка двух
векторов
4.3. Поп-стат, или Линейная
интерполяция
Рис. 4.2. Линейное сглаживание
Рис. 4.3. Определение точки с
максимальным отклонением от прямой
Рис. 4.4. Аппроксимация полиномом
3-й степени
Рис. 4.5. Сглаживание с
использованием функции linfit
Рис. 4.6. Нелинейное сглаживание
Рис. 4.7. Линейная интерполяция
Рис. 4.8. Интерполяция сплайном
Рис. 4.9. Интерполяция полиномом
Рис. 4.10. Двухмерная сплайн-интерполяция
Рис. 4.11. Сообщения об ошибках:
пользовательские и встроенные
Рис. 4.12. Примеры работы
двухмерной сплайн-интерполяции
Рис. 4.13. Пример одномерной
сплайн-интерполяции
Рис. 4.15. Примеры работы функции supsmooth
4.9. Экспертная оценка качества
чего-либо
Рис. 4.16. Оценка качеств менеджера
(начало)
Рис. 4.17. Оценка качеств менеджера
(окончание)
В данном этюде разговор о статистике ограничится рассмотрением
методов сглаживания, интерполяции и экстраполяции экспериментальных данных. Это одна из типовых
инженерных и научно-технических задач, заслуживающая отдельного этюда.
4.1. Заяц
Чтобы приготовить рагу из зайца, нужно иметь как минимум зайца. Чтобы обработать (сгладить,
аппроксимировать, интерполировать, экстраполировать и т.д.) экспериментальные
данные, нужно иметь как минимум эти
данные.
Чаще всего экспериментальные
данные представляют собой набор пар чисел (Xi, Yi), где Yi – экспериментальные значения некоторой искомой
функции, а Xi – значения
аргумента.
Рис. 4.1. Ввод и сортировка двух векторов
В пункте 1 на рис. 4.1
переменным X и Y присваиваются
транспонированные векторы-строки, а не просто векторы-столбцы. Это делается для
компактности записи. Кроме того, элементы векторов имеют лишние нули – 4.0
вместо 4 и т.д. За счет этого выравниваются по вертикали пары значений Xi и Yi. Без такой
маленькой хитрости рано или поздно пары собьются, что будет мешать их просмотру
и редактированию. Альтернативное решение этой проблемы – хранение пар данных в
матрице с двумя строками и с числом столбцов, равным числу пар[1].
Считается, что программиста
от простого смертного можно отличить по простому тесту. Если программиста
поставить в голову шеренги и приказать: «По порядку
рассчитайсь!»,
то программист сначала уточнит, по какой системе нужно рассчитываться
(двоичная, восьмеричная, шестнадцатеричная, десятеричная[2]...),
а потом выкрикнет: «Нулевой!» В среде Mathcad по умолчанию номер первого
элемента вектора (первого ряда и первого столбца матрицы) нулевой. Именно
поэтому при семи экспериментальных точках, координаты которых заносятся в
векторы X и Y, константа N равна шести (феномен
программиста в строю). Номер первого элемента массивов и векторов хранится в
системной переменной ORIGIN (an origin – начало, источник), значение которой (по умолчанию
оно нулевое) в Mathcad-документе можно изменять (ORIGIN:=1, например). Допустимо менять и второе умолчание
«шеренги» – систему счислений.
Ввести в среде Mathcad
переменную-вектор можно двумя различными способами (см. этюд 1): отдачей
команды Matrices из меню Math (Insert
– Mathcad 7 и 8)
либо нажатием на панели математических инструментов кнопки с изображением
матрицы (щелкнув по ней курсором мыши) – см. рис. 1.7. Ввод за переменной ее
индекса также допустим двумя способами: нажатием на панели математических
инструментов на кнопку-иероглиф «Переменная с индексом» или набором за именем переменной
символа открывающихся квадратных скобок (рудимент языков Pascal и C, где
квадратные скобки означают индексную переменную).
Векторы X и Y совсем не обязательно
вводить в Mathcad-документ вручную с клавиатуры. Если экспериментальный стенд
оборудован средствами АСНИ (автоматизированной системой научных исследований) и
данные с приборов заносятся на магнитный диск, то Mathcad-выражение X:=READPRN(имя файла) поможет
считать их и оформить в виде Mathcad-вектора (матрицы) с именем X[3]. Кроме
того, не следует забывать, что Mathcad – это полноценное Windows-приложение со
встроенными средствами обмена в статике и динамике (Clipboard, DDE, OLE). Объемную задачу можно решить лишь тогда, когда
голос Mathcad звучит в стройном хоре других приложений (графические, текстовые
и табличные процессоры, базы данных, языки программирования и т.д.).
4.2. Сортировка
Пары экспериментальных
данных перед дальнейшей обработкой желательно отсортировать по возрастанию
значений X. Это можно
сделать вручную, переставив местами две первых пары, как в нашем случае (пункт
1 рис. 4.1), или (при объемных массивах данных) автоматически через функцию csort (пункт 2
рис. 4.2), возвращающую упорядоченную матрицу по отмеченному номеру столбца (у
нас это нуль[4] –
второй аргумент функции csort). Для
этого оба вектора-столбца X и Y сливаются в матрицу M с двумя столбцами, которая после сортировки
расчленяется на те же, но уже упорядоченные векторы-столбцы. Это приходится
делать из-за того, что некоторые функции Mathcad (например, linfit, о которой
речь пойдет ниже) отказываются иметь дело с неотсортированным вектором. Да и
вообще, как говорят немцы, Die Ordnung muß sein! – Должен быть порядок!
4.3. Поп-стат, или Линейная интерполяция
Встроенные функции intercept (to
intercept по-английски – отложить отрезок на линии) и slope (наклон)
решают самую простую и самую распространенную задачу линейного сглаживания[5]
экспериментальных данных методом
наименьших квадратов (см. пункт 3.1).
Рис. 4.2. Линейное сглаживание
Задача аппроксимации, и не
только линейной – это типичная оптимизационная задача (см. этюды 2 и 3 и линии
уровня в пункте 3.2 на рис. 4.2), сводящаяся к поиску минимума целевой функции СКО (среднеквадратичное
отклонение) двух переменных a и b. В свою очередь, линейное сглаживание сводится к решению
системы линейных алгебраических уравнений (см. этюд 1 и пункт 3.3 на рис. 4.2),
состоящей из приравненных к нулю частных производных функции СКО по коэффициентам a и b.
Решение, показанное в пункте
3.2, предпочтительней для сферы образования – оно как бы «кричит» о сути метода
наименьших квадратов: в функции СКО фигурирует квадрат, а сама функция минимизируется.
Рис. 4.3. Определение точки с максимальным отклонением от прямой
Найденные тем или иным
способом значения коэффициентов a и b
сглаживающей функции y(x)
= a + b×
x позволяют построить на графике
прямую с роящимися вокруг нее точками (у нас квадратиками – рис. 4.3). Подобным
графиком на практике, как правило, завершают обработку экспериментальных
данных: график, во-первых, даст наглядное представление о качестве сглаживания,
а во-вторых, поможет в случае чего отловить допущенные ошибки ввода исходных
данных (пропуск десятичной точки, например). Этой цели может служить и
предварительная сортировка векторов (см. пункт 2 на рис. 4.1): ошибочные
значения (промах эксперимента, неправильный ввод данных) часто всплывают на
концах упорядоченного вектора. В-третьих, график сам по себе ценен. С помощью
графика, то есть с другого конца, можно довольно быстро решить задачу линейного
сглаживания. У автора в лаборатории есть сотрудница, у которой глаз-алмаз: она при помощи тонкой
прозрачной линейки так проводит прямую вблизи экспериментальных точек, что по
ней можно определить коэффициенты a и b с точностью не меньше трех процентов (толщина
карандашной линии).
Несколько слов о графических
возможностях Mathcad и других подобных пакетов. Если студент начнет строить
график функции по технологии, заложенной в математическом пакете, то автор
выгонит такого студента с занятий, да притом вослед будет улюлюкать и топать
ногами. Все (скажем осторожнее – почти все) математические пакеты при
построении графиков никак (почти никак) не используют элементы искусственного
интеллекта, а просто сканируют значение аргумента и проставляют точки с
заданным пользователем шагом или с шагом, определяемым разрешением дисплея
(принтера). Студентов же учат совсем другому – анализу функции, поиску
характерных точек (корней, минимумов, максимумов, точек перегиба и т.д.),
опираясь на которые и строится график: парабола, гипербола или какая-нибудь там
лемниската Бернулли (см. рис. 1.18 в этюде 1). Но Богу – Богово, кесарю – кесарево, машине – машиново. Беда многих
преподавателей в том, что они относятся к математическим пакетам не как к
инструментальным средствам, требующим определенной сноровки и навыка (и головы,
конечно), а как к своим своеобразным коллегам, которых на пушечный выстрел
нельзя подпускать к студентам, изучающим математику, дабы они (студенты) не
набрались от них (от пакетов) разных глупостей. Дежурная фраза одной знакомой
автора: «Mathcad – круглый дурак, Maple –
полный кретин, Mathematica – законченная идиотка».
Нелишне дополнить результаты
сглаживания указанием точки, максимально отклонившейся от прямой (см. рис.
4.3). Само значение такого выброса найти несложно через функцию max. А вот с определением
координат этой точки придется повозиться: привлечь аппарат булевых выражений,
принимающих два значения – True (в среде Mathcad – единица) и False (нуль),
умножение которых на текущий индекс фиксирует искомую координату.
В пакете Mathcad более 50
встроенных операторов (см. приложение 2) и почти 300 функций (см. приложение
3). Пять встроенных функций (csort, intercept, slope, min и max) были задействованы в
задачах на рис. 4.1-4.3. Когда программисту предстоит решать какую-либо
локальную задачу, то перед ним часто встает альтернатива: кодировать ли решение
прямо в программе или выносить его наружу, оформляя в виде процедуры (функции).
Считается, что глупый человек учится на своих ошибках, а умный – на чужих.
Начинающий программист пишет свои процедуры (функции), а опытный ищет их в
наборе ранее созданных. Знание пакета Mathcad – это на 90% знание операторов и
функций[6],
в него встроенных. Остальное – ловкость рук и программирование (средство
создания новых инструментов – см. этюд 6).
Есть три причины,
заставляющие даже сверхумного программиста отказываться от готовых программных
форм и «изобретать велосипед». Первая причина лежит в сфере образования: тексты
программ должны быть прозрачными для
обучаемых. Во-вторых, в открытый участок программы легко ввести дополнения и
изменения, расширяющие сферу ее применения и/или снимающие ранее наложенные
ограничения. Так устроен, к примеру, пакет MatLab (разработка фирмы The Math
Works). В его состав входят исходные тексты на языке C всех встроенных процедур
и функций, так что пользователь перед включением их в работу может что-то
узнать о методах, заложенных в них, и/или прощупать их работоспособность.
В-третьих, всегда есть опасения, что в готовую программную форму затесалась чужая ошибка, которая, как бомба
замедленного действия, может взорвать всю программу в самый неподходящий момент
– после сдачи готового программного продукта заказчику или после того, как он
разойдется по дилерской сети. Пример у нас под рукой (рис. 4.3). При всем
богатстве встроенных функций пакету Mathcad не хватает функции определения в
векторе или в матрице координат минимального (максимального) элемента. Выход из
положения – это сумма (для вектора) или двойная сумма (для матрицы) произведений
номера текущего элемента на булево выражение (см. рис. 4.3). Эту конструкцию
так и хочется оформить в виде новой функции с именем imax, например,
и больше с такой задачей не возиться. Но в новую функцию перекочует и будет
замаскирована ошибка – неясно, что будет возвращать новорожденная функция imax, если в
аргументе-векторе (в массиве) два или более максимальных элементов. Из
прозрачной формулы с суммой это понятно, а из «затененной» функции imax – нет. Все
эти замечания можно отнести и к встроенным функциям intercept и slope,
возвращающим значения коэффициентов сглаживающей прямой. Всегда остаются
сомнения, а нет ли в этих функциях фактической или методологической ошибки.
Последнюю можно обнаружить, если подставить в функции intercept и slope аргументы-векторы
с двумя или даже одним элементом. Через две точки всегда можно провести прямую.
Через одну точку прямых можно провести бесчисленное множество. И в том, и в
другом случае сумма квадратов отклонений двух точек (одной точки) от прямой
будет минимальной (нулевой), и требования метода наименьших квадратов будут
выполняться абсолютно. Но в первом случае функции intercept и slope будут
решать простую интерполяционную задачу, для которой в среде Mathcad есть особый
математический аппарат (см. ниже). Во втором случае (X и Y – не векторы, а скаляры)
функции intercept и slope должны
выдавать бесчисленное множество значений, связанных ограничением Y = a + b × X. В плане
выполнимости критерия наименьших квадратов здесь все безупречно, но
методология, заложенная в функции intercept и slope, приводит
к тому, что при числе элементов в векторах X и Y, меньшем
двух, выдается сообщение об ошибке. Но все это слабая защита, которую
пользователь легко может обойти, подсунув функциям intercept и slope более
одной точки, но с повторяющимися значениями аргументов. Резюме: играть можно не
только с игровыми программами. На эту роль подходят и серьезные математические
пакеты – было бы желание у пользователя. Компьютер же, как здоровая молодая
собака, всегда готов играть со своим хозяином. Замахнется, к примеру, человек
палкой, но не бросит ее, – собака прыгает, вертит головой, но не знает, куда
бежать. Подсунет пользователь машине хитрый аргумент – функция не знает, что с
ней делать, и выдает какие-то странные сообщения об ошибках, веселящие
пользователя.
Есть направление в искусстве
под названием поп-арт – популярное
искусство. Методика обработки статистических данных, показанная на рис. 4.2,
может быть названа поп-статом.
Рис. 4.New. Универсальный метод сглаживания
4.4. Полином
Исследователю,
обрабатывающему на компьютере свои экспериментальные точки, нет дела до всех
этих методологических тонкостей. Не напороться бы на фактическую ошибку, и на
том спасибо. Уже упоминавшийся KISS – принцип программирования призывает
пользователя прибегать к закрытым алгоритмам только в крайних случаях. При
поиске сглаживающего полинома Р-й степени
при Р, равном
единице (линейная задача), можно обойтись без функций intercept и slope, вспомнив,
что эта оптимизационная задача сводится к решению системы двух линейных
алгебраических уравнений. Полином более высокой степени потребует решения более
объемной, но все той же линейной системы.
Рис. 4.4. Аппроксимация полиномом 3-й степени
На рис. 4.4 формируются
матрица A
коэффициентов при неизвестных и вектор B свободных членов системы четырех линейных
алгебраических уравнений, к которой сводится задача об аппроксимирующем
полиноме третьей степени (кубическом). Сама система может решаться либо
матричными операторами (a:=A-1×B), либо обращением к встроенной функции lsolve (см. пункт
3.3.2 рис. 4.2). Полноценный программный пакет всегда должен предоставлять
пользователю возможность сделать какую-либо операцию двумя, а еще лучше тремя
различными способами. Пользователь будет чувствовать себя комфортно в
программной среде, если его право выбора не ограничено. На выбор же могут
влиять не только сомнения в качестве тех или иных готовых инструментальных
средств (см. выше) или нечеткое знание области их применения, но и вкусовые
предпочтения пользователя. Решение системы линейных алгебраических уравнений
(базовая задача любого Решателя)
через матричные операторы неудобно тем, что пользователь все время напарывается
на сообщения об ошибках, набирая R := B / A или R := B × A-1. Крамольность первого выражения
очевидна – в математике нет понятия матричного деления. Но почему нельзя писать
R := B × A-1, знают далеко не все. Так или
иначе, о KISS-принципе не следует забывать. Помнить следует и другое
предостережение, зафиксированное в пословице: «Простота хуже воровства». Выкладки рис. 4.4, от которых рябит в
глазах из-за обилия «сигм», можно упростить вводом переменных с индексом Ak,m и Bk (рис. 4.9).
Но! Автор уже раз обжегся на суммировании в среде Mathcad, когда рассматривал
систему искусственного интеллекта SmartMath (рис. 7.15 в этюде 7): за суммой,
особенно тройной с пересекающимися индексами, может таиться ошибка.
4.5. Полусвобода
Потребность в замене
сомножителей Xk полинома
более сложными формулами вызвала к жизни функцию linfit (LINear FITting – линейное сглаживание).
Рис. 4.5. Сглаживание с использованием функции linfit
Аргументы
функции
linfit – числовые векторы X и Y и
вектор-функция f, хранящая
набор пользовательских сомножителей (на рис. 4.5 – это 1, 1/x, 1/x2 и 1/x3),
коэффициенты которых функция linfit возвращает
в вектор a, опираясь
на метод наименьших квадратов (см. рис. 4.5).
4.6. Свобода
Рис. 4.6. Нелинейное сглаживание
1. В среде Mathcad есть
функция genfit (GENeral
FITting – общее сглаживание), допускающая множество параметрических
коэффициентов у сомножителей произвольного вида. Она, в отличие от функции linfit, решает нелинейную[7]
задачу аппроксимации. Пример использования функции genfit дан в
пункте 7.1 на рис. 4.6. В функцию-вектор f необходимо занести не только само сглаживающее
выражение (у нас это экспоненциальная функция), но и его частные производные[8]
по искомым параметрам a0
и a1,.объединенным
в вектор. Из-за того, что нелинейная задача может иметь более одного решения,
функция genfit требует
начального приближения (третий аргумент-вектор), вблизи которого и ищется одно
из решений.
2. Без функции genfit задачу
нелинейной аппроксимации, как правило, решают линеаризацией исходных данных, подключая к работе уже известные нам
функции intercept и slope. В нашем
случае (пункт 7.2 на рис. 4.6) при исходном уравнении Y=a × x b встроенные функции intercept и slope
прикладывают к новому уравнению Ln(Y)=Ln(a)+b×Ln(X). Но это приводит
к некоторому искажению математической модели: сумма X и сумма логарифмов X – это далеко не одно и то
же.
3. В ряде
случаев при решении задачи нелинейной аппроксимации можно обойтись и без
функции genfit (пункт 7.1
рис. 4.6), и без искажающей линеаризации (пункт 7.2), применив открытый
алгоритм поиска значений коэффициентов a0 и
a1, минимизирующих целевую функцию – сумму квадратов отклонений точек от
кривой. Расчет, показанный в пункте 7.3 на рис. 4.6, кроме того, не требует
знания частных производных сглаживающего уравнения.
В конце рис. 4.6 приведено
графическое сравнение трех методов нелинейного сглаживания. Из графика видно,
что линеаризация исходных данных (пункт 7.2) привела к существенным искажениям
результата. Поиски же параметрических коэффициентов через функцию genfit (пункт
7.1) и через минимизацию (пункт 7.3) близки по результатам.
Практический совет по выбору
наиболее подходящей формулы для сглаживания. В Mathcad-документе можно хранить
набор формул, подключая одну из них по мере надобности к статистической
обработке экспериментальных точек. В диалоговом окне Properties (свойства – оно вызывается командой Properties в меню Format) есть переключатель Disable Evaluation (Запретить
вычисления), позволяющий превращать математические выражения[9]
в комментарий:
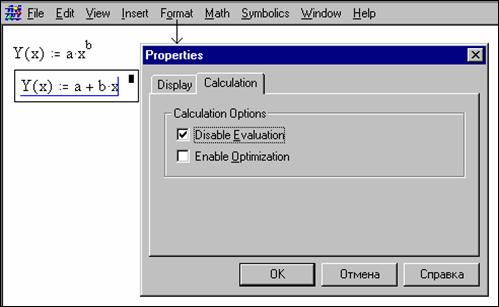
Данный переключатель
превращает выражение в комментарий (что отмечено черным квадратиком правее
выражения) и переопределяет тем самым функцию пользователя. О втором
переключателе (Enable Optimization – Разрешить
оптимизацию) будет рассказано в этюде 7 (раздел 7.3).
В Mathcad-документе можно
записать множество функций пользователя, подключая одну из них к аппроксимации:
линейной (рис. 4.2), экспоненциальной (рис. 4.6), логарифмической и т.д., и
подбирая тем самым наилучшую модель обработки экспериментальных данных. Выбор
формулы можно вести и без переключателя Disable Evaluation, опираясь на свойство среды
Mathcad включать в расчеты только последнюю запись функции. Нужную функцию
можно просто перетаскивать (технология drag-and-drop) в конец списка.
4.7. Опять полусвобода
При обработке данных
эксперимента, разбросанных «как попало», часто хочется плюнуть на критерии
оптимизации и просто провести линию (кривую или, на худой конец, ломаную,
состоящую из прямых отрезков) непосредственно через точки. Благо в среде
Mathcad есть для этого инструментарий: средства линейной интерполяции (функция linterp – рис. 4.7) и интерполяции
сплайном (interp – рис.
4.8) – линейным (lspline),
параболическим (pspline) и
кубическим (cspline).
Рис. 4.7. Линейная интерполяция
Рис. 4.8. Интерполяция сплайном
Отличия в линейной (lspline), параболической (pspline) и кубической (cspline) интерполяции сплайном заметно проявляются только на
концах отрезка X1-XN. Эти
области на рис. 4.8 рассмотрены «под лупой». Здесь нужно говорить уже не об
интерполяции, а об экстраполяции (см.
ниже рис. 4.14)
Несложно через точки
провести полином N-й степени
(рис. 4.9):
Рис. 4.9. Интерполяция полиномом
Но нанизать опытные точки на интерполяционный «шампур»,
напрочь игнорируя неизбежные ошибки эксперимента, может только совсем
безграмотный исследователь. У интерполяции другие сферы применения. Расскажем
об одной из них. При решении в среде Mathcad какой-либо задачи нередко
образуется составная функция[10], обращение
к которой вызывает длинную цепочку сложных вычислений, связанных с поиском
корней уравнения, с дифференцированием, интегрированием и т.д. Работать с
такой функцией становится невмоготу даже на мощном компьютере. Один из выходов
– омолаживание «бабушки»: табулирование «тормозной» функции с последующей
заменой ее на эрзац-функцию, опирающуюся на интерполяцию – линейную, нелинейную
или сплайном. И что удивительно, «омоложенная» функция, хоть и теряет напрочь
свою физику, но в особых условиях может возвращать более точное значение, чем
ее прародительница, в которой накапливаются ошибки численных методов. Узлы же
интерполяции можно просчитать на пределе точности.
4.8. Еще немного статистики
На рис. 4.10
показано, как функция lspline может
сгладить уже не линией, а поверхностью
экспериментальные точки двухфакторного эксперимента с помощью двухмерной
сплайн-интерполяции. У нас есть уже не вектор, а матрица экспериментальных точек, зависящих от двух переменных
эксперимента: температуры пара (T) и его давления (P – см. www.wsp.ru).
Рис. 4.10. Двухмерная сплайн-интерполяция[11]
Далее автор приводит несколько
пронумерованных «Советов тем, кто работает с Mathcad», которые публикуются в
журнале КомпьютерПресс – на бумаге и на прилагаемом к журналу лазерном диске.
Педагогический
опыт автора[12]
говорит о том, что студенты, выполняющие термодинамические расчеты, очень часто
ошибаются в размерностях: складывают, например, джоули с британской единицей
теплоты, а ответ записывают в калориях, забывая о соответствующем пересчете. Мы
этой темы уже подробно коснулись в этюде 1. Среда Mathcad позволяет правильно
(с соответствующими пересчетами) оперировать размерными величинами и «ругается»
только в крайних случаях, когда, например, складывается длина с массой. Наша
пользовательская функция h(T, P) возвращает
размерную величину (удельная энтальпия перегретого водяного пара), а ее
аргументы (давление и температура пара) – также размерные величины.
Совет 25.
Формируя
пользовательскую интерполирующую функцию, необходимо сразу освободиться от
размерностей аргументов, приведя их к безразмерной величине относительно данных
в боковике (у нас это температура) и шапке (давление) таблицы узловых (опорных)
точек. Размерность функции, соответствующая данным в таблице, приписывается к
возвращаемой величине в конце формируемой функции.
Все это
позволяет иметь в качестве аргументов функции величины с любой допустимой
размерностью температуры и давления и получать удельную энтальпию также с
различной размерностью (см. рис. 4.10).
Совет 26.
Интерполяция,
как правило, ведется в оговоренном диапазоне значений аргументов. Поэтому будет
целесообразно вставить в функцию пользовательские
сообщения об ошибке – о выходе за пределы разумных значений аргументов[13].
Для этого предназначена встроенная в Mathcad функция error(“Сообщение об ошибке”),
прерывающая выполнение вычислительной процедуры и своим комментарием
призывающая пользователя исправить оплошность. Если пользователь «подсунет»
функции h(T,
P), к примеру, не температуру и давление, а массу и длину, то заработает
уже встроенное сообщение об ошибке “The units in the expression do not match”
(Единицы в выражении не соответствуют правилам – см. рис. 4.11):
Рис. 4.11. Сообщения об ошибках: пользовательские и встроенные
Совет 27.
Методика
двухмерной сплайн-интерполяции, реализованная в Mathcad, требует, чтобы
табличные значения двух аргументов хранилась в матрице с двумя столбцами, а
табличные значения функции – в квадратной матрице. Для лучшего обзора и
редактирования табличные данные можно временно объединить в одной квадратной матрице
(у нас ее имя M, а размер (порядок) 19 на 19 – см. рис. 4.10), где
первый столбец без первого элемента – это табличные значения температуры
(первый аргумент формируемой функции), а первая строка без первого элемента –
табличные значения давления (второй аргумент). Последующие манипуляции функцией
submatrix раскладывают все «по полкам» –
матрица TP с двумя столбцами и с 18
строками хранит табличные значения аргументов, а квадратная матрица H с порядком 18 – табличные значения удельной энтальпии. Так
можно добиться компромисса между требованиями Mathcad и требованиями наглядного
размещения данных.
Для лучшего
обзора исходных данных и для разделения их на функциональные группы в исходной
матрице можно записывать числовые константы (элементы матрицы) с различным видом и размером шрифта – см.
рис. 4.10 (непронумерованный совет).
Совет 28.
Никогда не
стоит опираться на конкретное значение
системной переменной ORIGIN (номер
первой строки и первого столбца матриц) и на конкретный размер матриц. В
функции h(T,
P) записан оператор «вырезания куска» из матрицы M
– вектора табличных значений температур:
TP<ORIGIN>¬submatrix(M,
ORIGIN + 1, rows(M) - 1, ORIGIN + 1, cols(M) - 1),
а не
TP<0>¬submatrix(M, 1,
18, 1, 18)
Два эти
выражения эквивалентны только при ORIGIN=0 (умолчание
Mathcad) и при порядке матрицы M, равном 19. При других значениях
переменной ORIGIN и при
других размерах матрицы M второе
выражение при вызове функции h даст сбой.
Совет 29.
Очень часто
табличные данные, отображающие значения какой-либо физической величины
(удельной энтальпии водяного пара, как в нашем случае), не укладываются в
отведенные им в среде Mathcad сугубо квадратные рамки. На место отсутствующих
данных (левый нижний и правый верхний угол нашей квадратной матрицы) можно
записать что-то, резко отличающееся от «настоящих» данных. У нас это минус
единица. Возврат значения функции нужно предварить оператором error (см.
предпоследнюю строку на рис. 4.10), прерывающим расчет, если возвращаемое
значение «не лезет ни в какие ворота» в смысле порядка величины. В нашем случае
с функцией h(T,
P) значение энтальпии не может быть меньше, чем 1930.8 кДж/кг – наименьшее
«разумное» значения матрицы энтальпий. Если так получилось, то это означает,
что при интерполяции «захвачена» минус единица и решение неверно.
Совет 30.
При подготовке Mathcad-документа к публикации
стоит переместить копию экрана дисплея (клавиша PrtSc) в среду какого-либо графического редактора (Paintbrush, например) и там его доработать.
Основные направления доработки, которыми автор воспользовался, готовя
иллюстрации к этой книге:
·
вертикальная линия, отмечающая начало и конец
процедуры формирования функции пользователя h(T, P) на рис. 4.10, изогнута, что позволило сделать листинг
более компактным;
·
для этой же цели были убраны столбцы, хранящие
энтальпию пара при 8, 10, 12, 15, 20 и 22 МПа;
·
в среде графического редактора в Mathcad-документ
можно внести то, что в среде Mathcad не внесешь, например, вертикальный
комментарий на месте стертых столбцов и другие пометки – см. рисунки книги;
·
копируя экран дисплея, можно захватить информацию,
которая при простой распечатке Mathcad-документа (команда Print в меню File) пропадает. Это, во-первых, встроенные и пользовательские
сообщения об ошибках – см. рис. 4.11. Можно из разных копий экрана дисплея,
фиксирующих различные моменты диалога пользователя с компьютером, собрать один:
на рис. 4.11 выведены все три сообщения об ошибках, хотя на экране дисплея
одновременно можно видеть лишь одну – ту, которая выпадает из «покрасневшей от
ошибки» функции, когда пользователь наводит на нее курсор мыши.
На рис. 4.12 проиллюстрирован вызов функции h(T, P) при различных значениях и
различных размерностях аргументов. Размерность возвращаемой функцией удельной
энтальпии пользователь также вправе менять.
Рис. 4.12. Примеры работы двухмерной сплайн-интерполяции
На рис.
4.13 приведен пример формирования с помощью одномерной сплайн-интерполяции еще
одной важной термодинамической функции одного аргумента – зависимости удельного
объема кипящей воды от ее температуры.
Рис. 4.13. Пример одномерной сплайн-интерполяции
Сплайн-интерполяция особенно
критична на границах отрезка (области) существования аргументов. Вне этих
границ речь идет уже не об интерполяции, а об экстраполяции – о предсказании
значений функции за границами отрезка.
На рис. 4.14 показана работа
функции predict, с помощью
которой предсказывается поведение
какой-либо зависимости.
Рис. 4.14. Экстраполяция
У функции predict (prediction –
предсказание) три аргумента: вектор имеющихся данных (у нас 100 значений
функции y(x) на
интервале от 0 до 99 с шагом 1), число последних данных, учитываемых в
предсказании (у нас их 50) и число предсказываемых данных (100). На графике на
рис. 4.14 толстая кривая – функция y(x) на
интервале 0-99, тонкая кривая – функция y(x) на интервале 100-199, а
квадратики – предсказанные значения (не все, а только кратные 5), которые
где-то в районе 160-170 обрываются.
Задание читателю,
подготавливающее его к чтению следующего этюда, где будет описана
математическая модель одной финансовой операции, – предсказать курс доллара на
будущую неделю, опираясь на данные предыдущего месяца или года.
На рис. 4.15
проиллюстрирована работа сглаживающей функции supsmooth. Решается
такая задача – сгладить функцию стоимости, например, комплектующих компьютера
(см. задачу на рис. 6.33-6-35) в зависимости от объема закупки (скидка
оптовикам).
Рис. 4.15. Примеры работы функции supsmooth
4.9. Экспертная оценка качества чего-либо[14]
Качество есть качество. Качество нельзя измерить[15],
но можно оценить. Существуют две формы оценки качества: лингвистическая и
количественная. В первом случае качество определяют словами: например, «качество высокое», «среднее», «низкое» и
т.д. Во втором случае качество оценивают по некоторой условной шкале числом K (0 ≤ K
≤ M, где M - высший балл в числовой оценке качества). Например, «пять»,
как в российской, или 100 как в английской школах.
Для оценки качества привлекаются эксперты. Экспертной оценке качества могут быть подвергнуты товары
и услуги, проекты и законы, знания и квалификация, выступления фигуристов,
гимнастов или вокалистов и многое другое.
В повседневной жизни при принятии решения можно исходить из
лингвистической оценки качества: мы покупаем хороший чай или инструмент высокого
качества (если позволяют средства). Однако есть такие задачи, в решении
которых лучше руководствоваться количественной оценкой качества. Кроме того,
обычно лингвистические оценки строятся на основе экспертных количественных
оценок. Так, качество выпускника английского университета и достоинство
диплома, который он получает, определяется по следующей шкале:
|
Средний балл в интервале оценок по 100-бальной шкале |
Достоинство диплома (лингвистическая оценка) |
|
90 - 100 |
С отличием |
|
85 - 90 |
Первой ступени А |
|
80 - 85 |
Первой ступени Б |
|
70 - 80 |
Второй ступени |
|
менее 70 |
Обычный |
Независимо от объекта, качество которого подлежит экспертной
оценке, методика ее получения в основе своей одинакова.
Рассмотрим задачу оценки деловых
качеств руководителя (менеджера). Для оценки потребуются модель качества
менеджера, эксперты и математическая обработка результатов работы экспертов.
Модель качества специалиста может быть представлена в виде
некоторого набора важнейших качественных параметров (качеств), характеризующих
его профессиональный уровень, личностные, деловые качества и предопределяющих
успешную работу в рассматриваемой сфере деятельности.
Допустим, что этот набор включает
следующие качества:
1) уровень и качество образования, опыт практической работы,
2) эрудиция, знания и умения в своей и смежных сферах
деятельности,
3) обучаемость и способность обучать,
4) культурный уровень, моральные стандарты,
5) физическое и психологическое здоровье, возраст,
6) характер, отношение к окружающим,
7) умение руководить,
8) амбициозность, стремление к лидерству,
9) способность к риску,
10) динамизм (способность оценивать и принимать изменения
внутренней и внешней среды).
Эксперты располагают данными (анкеты, опросные листы,
результаты тестов и прочее), позволяющими оценить по пятибалльной системе
степень принадлежности качества кандидату. Пятибалльная система привычна и
обеспечивает возможность представительной оценки степени принадлежности
качества кандидату, например, по следующему алгоритму:
|
Принадлежность качества кандидату |
Оценка в баллах |
|
отсутствует |
1 |
|
проявляется в слабой степени |
2 |
|
проявляется |
3 |
|
проявляется явно |
4 |
|
присуще в полной мере |
5 |
Результатом работы экспертов станет таблица оценок каждого из десяти качеств модели каждым экспертом[16] (количество экспертов определяется важностью решения и средствами, выделенными на экспертизу).
Рис. 4.16. Оценка качеств менеджера (начало)
В пункте 1
на рис. 4.16 оценки экспертов введены в матрицу M,
содержащую девять строк (число экспертов n, j=1..9) и десять
столбцов (число качеств m, i=1..10).
Пятибалльная средневзвешенная оценка деловых качеств
менеджера определяется по формуле:
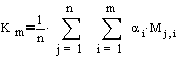 (4.1)
(4.1)
где m –
количество оцениваемых качеств,
i := 1, 2.. m,
n – число
экспертов, j
:= 1, 2.. n,
Мj,i – оценка j-м экспертом i-го качества в баллах,
ai – весовой
коэффициент для i-го качества.
Весовые коэффициенты определяют относительную значимость
качеств: если i-е качество
представляется незначимым, то весовой коэффициент ai равен
нулю. Придание коэффициенту ai значения, равного единице, делает незначимыми все
остальные качества. Весовые коэффициенты должны удовлетворять следующему
условию:
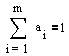 (4.2)
(4.2)
Значения весовых коэффициентов
могут быть установлены различными способами:
·
лицом, принимающим решения (ЛПР);
·
экспертом с соблюдением условия (4.2);
·
по результатам экспертных оценок качества, косвенно
отражающих мнения экспертов о значимости оцениваемых характеристик.
В последнем случае весовые
коэффициенты рассчитываются по формуле:
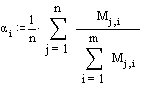 (4.3)
(4.3)
Вычисленные значения весовых коэффициентов в табличной и
графической формах представлены в пункте 3 на рис. 4.17.
Рис. 4.17. Оценка качеств менеджера (окончание)
Средневзвешенная оценка качества менеджера в баллах (пункт 4
на рис. 4.17) ¾ Kм = 4.162.
Алгоритм определения весовых коэффициентов ai влияет на оценку качества, которая может быть
выполнена по выбору ЛПР на основе гипотезы равной значимости весовых
коэффициентов:
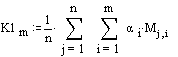
где ai = 1 / n.
В этом случае оценка качества значительно возрастает (в
сравнении со средневзвешенной оценкой) – K1м = 4.593.
Значения весовых коэффициентов могут быть установлены с
учетом специфики конкретного заказа из условия приоритета качеств (требуется «высокий» профессионал,
личность приятная во всех отношениях, но без особой склонности к руководству).
В этом случае приоритеты могут быть установлены, например, на следующих
значениях: для профессиональных качеств ¾ kп1=1.15,
личностных ¾ kп2 =1.05, деловых ¾ kп3 =0.8. Значения
весовых коэффициентов для групп качеств r определяются формулой:
(ar)i = kпr / n, где
n
= 9, r= 1, 2, 3,
и равны – (a1)i = 1.15 / 9 = 0.128; (a2)i = 1.05 / 9 = 0.117; (a3)i = 0.8 / 9 = 0.089.
Вектор-строка
весовых коэффициентов имеет вид:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
(ar)I |
(a1)i |
(a1)i |
(a1)i |
(a2)i |
(a2)i |
(a2)i |
(a3)i |
(a3)i |
(a3)i |
Средневзвешенная оценка качества менеджера в баллах (пункт 8 на рис. 4.17) ¾
Kм
= 4.496.
Итак, в рассмотренном примере в зависимости от способа
определения весовых коэффициентов получены три оценки качества:
Km = 4.162 – при экспертной оценке a;
K1m = 4.593 – случай равнозначимых весовых
коэффициентов;
K2m = 4.496 – при приоритете (kп1=1.15)
профессиональных качеств.
Выбор кандидата – прерогатива лица, принимающего решение, или
конкурсной комиссии.
Рассмотренная методика применима для оценки качества
продукции, результатов испытаний, экзаменов и других задач экспертной оценки.
Возможно, руководителю группы экспертов или заказчику
экспертизы потребуется анализ результатов работы экспертов для оценки их
компетентности, пристрастий или добросовестности.
Весовые коэффициенты i-го качества в оценке j-го эксперта рассчитываются
по формуле
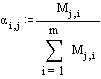
Результаты расчета содержатся в матрице a (пункт 5 на рис. 4.17).
Для наглядного представления результатов работы экспертов,
анализа оценок, близости объекта к эталону качества в некоторых задачах очень
удобна радарная диаграмма (Radar-diagram). Пример –
экспертиза проекта электростанции по таким показателям: экономичность,
экологичность, архитектурные решения, совместимость с еще не подпорченным
ландшафтом, безопасность, надежность, значимость для экономики региона и др.
Для всех показателей из центра диаграммы проводятся лучи, на которых откладываются
средние значения оценок экспертов. Соединив точки на лучах, получим
многоугольник. Эталону качества будет соответствовать вписанный в окружность с
радиусом М (М – высший балл по шкале
оценок) правильный многоугольник[17].
Степень приближения к эталону наглядно представляется формой и относительной
площадью получившегося на основе оценок экспертов многоугольника (пункт 2 на
рис. 4.6).
Тема оценки качества далеко не
исчерпана. Интересные решения могут быть получены с использованием теории
нечетких множеств (см. этюд 6).