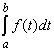Приложение 2

Встроенные операторы Mathcad 8 Pro

Обозначения:

A и B – массивы (вектора или матрицы);

u и v – векторы с действительными или комплексными элементами;

M – квадратная матрица;

z и w – действительные или комплексные числа;

x и y – действительные числа;

m и n – целые числа;

i – диапазон переменных;

t – любое имя переменной;

f – функция;

X и Y – переменные или выражения любого типа.

Оператор	Написание в среде Mathcad	Горячая клавиша	Описание
Присвоить значение полуглобальной переменной (элементу массива, столбцу матрицы) определить функцию пользователя	■ := ■ a := b + c Mi,j := 5 M^<2>:= V z(x, [y, …]) := x+5	:	Присваивает значение переменной (элементу массива), определяет функцию пользователя, видимую правее и ниже данного оператора
Присвоить значение глобальной переменной (элементу массива, столбцу матрицы), определить функцию пользователя	■ º ■ a º b + c Mi,j º 5 M^<2>º V z(x, [y, …]) º x+5	~	Присваивает значение переменной, определяет функцию пользователя, видимую во всем Mathcad-документе
Присвоить значение локальной переменной (элементу массива, столбцу матрицы)	■ ¬ ■ a ¬ b + c Mi,j ¬ 5 M^<2>¬ V		Присваивает значение локальной переменной, видимой только в программном блоке
Вычисление числового значения	■ = ■ [■] a = 23.45 L = 34.56 m f(x) = 21 Vi = 5		Вычисляет и выводит на дисплей во второй операнд числовое значение переменной, выражения, функции, записанной в первом операнде. Можно задавать размерность (третий операнд)
Круглые скобки	(X)	‘	Группа операторов
Нижний индекс	An	[	Возвращение индексированного элемента массива
Верхний индекс	A^<n>	[Ctrl]6	Выбор колонки n из матрицы A. Возврат вектора
Векторизация		[Ctrl]-	Позволяет производить операции по экспрессии X для того, чтобы один элемент заменялся другим. Все векторы или матрицы в X должны быть одинакового размера (рис. 4.6)
Факториал	n!	!	Возвращает n×(n-1)×(n-2)... Целое число n не может быть отрицательным.
Сопряженный комплекс		“	Инвертированный сигнал мнимой части X
Транспонировать	A^T	[Ctrl]1	Возвращает матрицу, чьи ряды являются колонками A и чьи колонки являются рядами A. A может быть вектором или матрицей (рис. 4.1)
Степень	z^w	^	Возводит z в степень w
Степень матрицы, инверсная матрица	M^n	^	n^th – степень квадратной матрицы M (использование матрицы умножения). n должно быть целым числом. M^-1обратно пропорционально M. Другие отрицательные степени являются степенями инверсий. Возврат матрицы
Отрицание	-X	-	Умножение X на -1
Сумма вектора	Sv	[Ctrl]4	Суммы элементов вектора v; возвращает скаляр
Квадратный корень		\	Возвращает положительный квадратный корень для положительного z; абсолютную величину для отрицательного или комплексного z (рис. 2.2, 2.3, 2.8)
Корень n-й степени		[Ctrl]\	Возвращает n^th корень z; возвращает реальное значение корня всякий раз, когда это возможно
Размер	|z|	|	Возвращение
Размер вектора	|v|	|	Возвращает , если все элементы вектора v являются вещественными. Возвращает, если элемент в v является комплексным
Детерминант	|M|	|	Возвращает определитель квадратной матрицы M
Деление	X/z	/	Деление выражения X на скаляр z, не равный 0. Если X является массивом, то мы делим каждый элемент массива на z
Умножение	X×Y	´	Возвращает произведение X и Y, если X и Y являются скалярами. Умножаем каждый элемент Y на X, если Y является массивом и X – скаляром. Возвращает точечное произведение (внутреннее произведение), если X и Y – векторы одинакового размера. Выполняет умножение матрицы, если X и Y являются подобными матрицами
Кросс- произведение	u×v	[Ctrl]8	Возвращение кросс-произведения (вектор произведения) для третьего элемента векторов u и v
Суммирование		[Ctrl] [Shift]4	Произвести суммирование X для i=m, m+1,... n. X может быть любым выражением. m и n должны быть целыми числами (рис. 3.3 и 4.9)
Произведение		[Ctrl] [Shift]3	Выполнить итерацию произведения X для i=m,m+1,...n. X может быть любым выражением. m и n должны быть целыми числами (рис. 2.7)
Границы суммирования		$	Возвращает сумму X ряда переменных i. X может быть любым выражением (рис. 4.2)
Границы произведения		#	Возвращает итерации произведений X над рядом переменных i. X может быть любым выражением
Предел		[Ctrl]L	Возвращает предел функции f(x) по мере того, как x приближается к значению a. Должно быть оценено символически (рис. 7.6)
Предел		[Ctrl]B	Возвращает предел функции f(x) по мере того, как x приближается к значению a с левой стороны. Должно быть оценено символически (рис. 7.6)
Предел		[Ctrl]A	Возвращает предел функции f(x) по мере того, как x приближается к значению a с правой стороны. Должно быть оценено символически (рис. 7.6)
Интеграл		&	Возвращает определенный интеграл f(t) на интервале [a, b]. a и b должны быть реальными скалярами. Переменные в выражении f(t), исключая переменную интегрирования t, определены (рис. 7.6). Подынтегральное выражение f(t) не может быть возвращено в массив
Неопределенный интеграл		[Ctrl]I	Возвращает неопределенный интеграл f(t). Должен быть оценен символически
Производная		?	Возвращает производную f(t) по t. Все переменные в выражении f(t) должны быть определены, переменная t должна иметь скалярное значение, функция f(t) должна возвращать скаляр (рис. 2.3)
n^th-я производная		[Ctrl]?	Возвращение n ^th-й производной от f(t) по t. Все переменные в f(t) должны быть определены, переменная t должна иметь скалярное значение, функция f(t) – скаляр. n должно быть выражено с помощью цифр 0, 1, 2, 3, 4, 5 или оценено символически каким-нибудь целым положительным числом (рис. 7.6)
Сложение	X+Y	+	Выполняет скалярное сложение, если X, Y или оба являются скалярами. Выполняет сложение элементов, если X и Y – векторы или матрицы одинакового размера. Если X является массивом и Y – скаляром, складывает каждый элемент Y и X
Вычитание	X-Y	-	Выполняет скалярное вычитание, если X, Y или оба являются скалярами. Выполняет вычитание элементов, если X и Y – векторы или матрицы одинакового размера. Если X является массивом и Y – скаляром, вычитает Y из каждого элемента X
Сложение с линией разрыва	X... +Y	[Ctrl][¿]	Работает точно так же, как сложение. Линия разрыва имеет редакционное значение (рис. 2.5)
Больше чем	x>y S1>S2	>	Возвращает 1, если x больше y, 0 – в других случаях. x и y должны быть скалярными переменными, хранящими действительное число; для текстовых переменных S1 и S2 – возвращает 1, если ASCII-кодировка переменной S1 больше, чем у переменной S2
Меньше чем	x<y S1<S2	<	Возвращает 1, если x меньше y, 0 – в других случаях. x и y должны быть скалярными переменными, хранящими действительное число; для текстовых переменных S1 и S2 – возвращает 1, если ASCII-кодировка переменной S меньше, чем у переменной S2
Больше чем или равно	x³y S1³S2	[Ctrl]0	Возвращает 1, если x больше либо равно y, 0 – в других случаях. x и y должны быть скалярными переменными, хранящими действительное число; для текстовых переменных S1 и S2 – возвращает 1, если ASCII-кодировка переменной S1 больше либо равна ASCII-кодировке переменной S2
Меньше чем или равно	x£y S1£S2	[Ctrl]9	Возвращает 1, если x меньше либо равно y, 0 – в других случаях. x и y должны быть скалярными переменными, хранящими действительное число; для текстовых переменных S1 и S2 – возвращает 1, если ASCII-кодировка переменной S1 меньше либо равна ASCII-кодировке переменной S2
Не равно	z¹w S1¹S2	[Ctrl]3	Возвращает 1, если z не равно w, 0 – в других случаях. z и w должны быть скалярными переменными, для текстовых переменных S1 и S2 – возвращает 1, если ASCII-кодировка переменной S1 не идентична ASCII-кодировке переменной S2
Равно	z=w	[Ctrl]=	Возвращает 1, если z равно w, 0 – в других случаях. z и w должны быть скалярами
Вычисление символьного значения	■ ®		Вычисляет символьное значение выражения
С плавающей запятой	■ float[,n] ®		Задает количество знаков после десятичной точки, выводимых на экран при символьном вычислении, по умолчанию выводит 20 знаков
Решить	■ solve ■ ®		Решить аналитически уравнение по заданной переменной или систему уравнений по переменным, заданным вектором
Разложить на множители	■ factor [■] ®		Раскладывает выражение на множители, если это возможно. Раскладывает по заданной переменной на один радикал или несколько радикалов, разделенных на простые радикалы. Переменная является опцией. Обычно раскладывает выражение с простыми переменными по степени значимости. В другом случае пытается преобразовать данное выражение в выражение, состоящее из простейших функций. Преобразует сумму дробей в простую дробь
Разложить по подвыражению	■ collect, ■, ■, ...,■ ®		Обеспечивает замену указанного выражения другим выражением, скомплектованным по базису указанной переменной или подвыражений
Преобразование Фурье	■, fourier ■ ®		Проводит преобразование Фурье относительно заданной переменной.
Обратное преобразование Фурье	■, invfourier ■ ®		Проводит обратное преобразование Фурье относительно заданной переменной
Представить в комплексном виде	■ complex ®		Представляет выделенное выражение в комплексном виде
Упрощение выражения	■ simplify ®		Упрощает выделенное выражение, выполняя арифметические действия, сокращая подобные слагаемые, приводя к общему знаменателю и используя основные тригонометрические тождества
Разложение по степеням	■ expand, [■] ®		Раскладывает выделенное выражение, представляя простые функции через более сложные, на сумму выражений по заданной переменной, по умолчанию – раскладывает выражение, пренебрегая этим. Если выражение – дробь, раскладывает числитель и пишет сумму дробей. Если выражение тригонометрическое – раскладывает его так, чтобы, насколько это возможно, оно содержало только синусы и косинусы
Разложить в ряд	■ series, ■, ■ ®		Раскладывает выделенное выражение в ряд Тейлора по заданной переменной с заданным числом членов ряда, по умолчанию выводит 6 членов ряда. Разложение возможно для функции заданной переменной
Преобразование Лапласа	■ laplace, ■ ®		Проводит преобразование Лапласа относительно заданной переменной
Обратное преобразование Лапласа	■ invlaplace, ■ ®		Проводит обратное преобразование Лапласа относительно заданной переменной
Игнорирование отдельных направлений символьных преобразований	■ assume, ■ ®		Игнорирование отдельных направлений символьных преобразований: переменная не комплексная, а вещественная и т.д.
Подстановка	■ substitute, ■ = ■ ®		Преобразует выражение в такое, где указанная переменная заменена на другую переменную или выражение (рис. 2.1)
Полиномиальные коэффициенты	■ coeffs, ■ ®		Находит коэффициенты выражения, если это выражение полином или может быть преобразовано в полином по заданной переменной или по заданному подвыражению
Разложить на элементарные дроби	■ convert parfrac, ■ ®		Представляет выделенное выражение в виде суммы правильных целых дробей относительно заданной переменной.
z-преобразование	■ ztrans, ■ ®		Проводит z-преобразование относительно заданной переменной
Обратное z-преобразование	■ invztrans, ■ ®		Проводит обратное z-преобразование относительно заданной переменной