6.9.6. A genuinely optimum fire bucket

(Translation into English by R.Girvin)

(Russian Text)

This optimization task was easily manageable either numerically (see Etude 2) or analytically (see Etude 7). In those, we learned how to maximise the volume of a bucket given a chosen manufacturing technology: cutting a sector from a metal disk and folding the remainder into a cone. But that way the bucket lost not only optimality, but also the status of bucket: it turned into a fire bowl! It was also impossible to put on a floor, and would be useless for any purpose except as a Vietnamese hat. In our rush for Number (the volume of the bucket) we have lost Essence (the function of a bucket, its capacity for conveniently carrying liquid).

The author recalls a cartoon film based on a Norwegian fable about a goat that learned to count, and decided to count all the farm animals: "I am one; the hen is two; the pig is three, etc." But as all the animals were moving around, the process soon turned into uproar. "Oh, have you counted me?!" "Keep still, or else..!" But everything ended happily, both for the goat and the fable.

In this story, as with any other fairy tale, there's a deep wisdom. It's necessary for us to count things, but as we interact with them we can run into a conflict. Not only does Nature dislike sharp corners, but also enumeration, which in a number of cases simply kills her. This can be observed not only in biology and physics, where the tools of knowledge frequently unrecognizably spoil the object of research, but also in computer science. This applies not only when applying computers to natural sciences applications, but also when applying computers to computers.

To establish a diagnosis, a doctor has no need to know the exact numerical value for a patient's body temperature (36.6C, 38.9C, etc). It's enough to express the thermometer indications by ranges, on which 'medics' have agreed beforehand: "low", "normal", "raised", "mild fever", "high fever". The borders of these estimates, though precisely fixed, are nevertheless imprecise – 'fuzzy'. This comes not merely from modern representations in terms of fuzzy set theory (FST) but also in terms of practical reality: thermometer error, measurement technique, and so on. A graduate of a medical school can tell you, without even pausing to think, where the division between high and very high temperature lies. The skilled doctor can decide this without consciously thinking of the number, while diagnosing better than the beginner.

Even the parameters of patients that are expressed not in real numbers, but in a kind of binary – Wasserman test positive/negative, Koch bacilli present/not present, HIV positive/negative, etc. – have 'fuzzy' borders. Laboratory analysts know this well. If you glance in any therapeutic reference book, where the symptoms of illnesses are described, normally you won't see hard numbers for body temperature, arterial pressure, haemoglobin count, etc. You'll simply see a broad categorisation: "is raised", "is lowered", and so on. Perhaps this is why programs that output a diagnosis, based on patient parameters entered into a computer, have not received wide practical application. One of difficulties in this area is translation of the parameter (a number) into a symptom (a category).

There's a generally accepted identification of three recent revolutions in programming: structural, object-oriented, and visual. But this revolutionary zeal focused more on the programs (the art for its own sake) and virtually neglected the point of programming: the models of the real world, the properties, and the events programs are simulating. Moreover, in retrospective we can see certain counter-revolutions: for example, the decline of analogue computers in favour of digital engineering. Recently, though, there has been a renaissance through the revival of principles of analogue modelling on modern digital computers (for example, the MathConnex environment included with Mathcad 7 and 8 Pro: see Appendix 7). It can similarly be seen in the technology of visual programming, where the former analogue control elements – adders, integrators etc. – are reconstructed.

But the virtual nature of these neo-analogue machines means also their strict determinism, and this brings not only positive, but also negative consequences. The principles of FST have been in programmers' hands for a long time – literally. The computer mouse reacts to two events: a click, and a double click. What, actually, is the difference one double click and two single? The duration of the pause between clicks. Expressed in non-technical language – "very short", "short", "long", etc.) this is a typical example of sets with 'fuzzy' borders. How much time is needed to increase a short pause to turn it into long, so that the double click breaks up into two single? How many handfuls of grain make a heap?

At the peak of the structural programming revolution, when in all the programming 'temples' the keyword GOTO was anathema, you frequently heard such statements as: "It's practically impossible to teach good programming to students originally taught BASIC; as potential programmers they're crippled intellectually, without hope of a cure." There were also broader warnings such as "Caution! Employment in programming is a dead end career. Don't think that having learned to program, you'll achieve anything in life".

It's as if traditional programming forces the programmer to look at the Technicolor world through monochrome glasses: a binary variable can take only two values (yes/no), and a real variable, values anywhere in a stipulated range strictly determined by the length of the mantissa. The truth lies somewhere between. The extreme points of view aren't useless – they are like book-ends that stop it sliding beyond defined extremes. The intermediate truths are termed 'fuzzy'. So one might say, "If you want to learn about the world (which is fuzzy, and unquantifiable) and to deal with it, beware of the traditional programming languages and mathematical programs with their strict determinism."

But we shall return to our problem of the fire bucket, and try to solve it using FST techniques and the opinions of people (who – thank goodness! – don't need such a rigmarole to use a simple device to escape being roasted).

Let's carry out an original poll and learn as much as we can about the parameters of an optimum fire bucket: its most convenient geometry (radius of the base of the cone to the height) and its optimum volume (the weight of the filled bucket). These can then be expressed as FST rules. How much water can you add to a bucket before it turns from light to heavy? How much can you increase or reduce the radius, or the height, of a bucket before it stops being convenient? These statements are typical definers of fuzzy sets. In the Mathcad environment, as well as in other popular packages, there are no variable types for storing such objects. But nevertheless we'll try to solve the given problem (see figures 6.41, 6.42, 6.43, 6.44 and 6.45 – a solution developed with B. Usyenko). Let's break it down into steps.

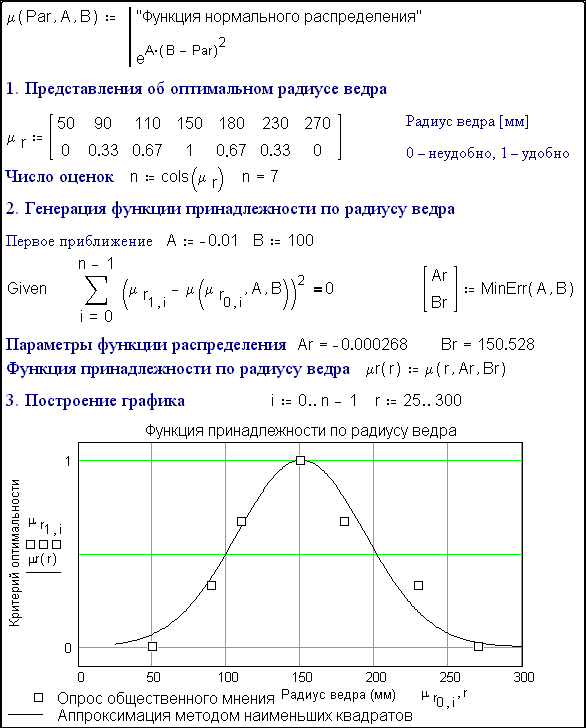
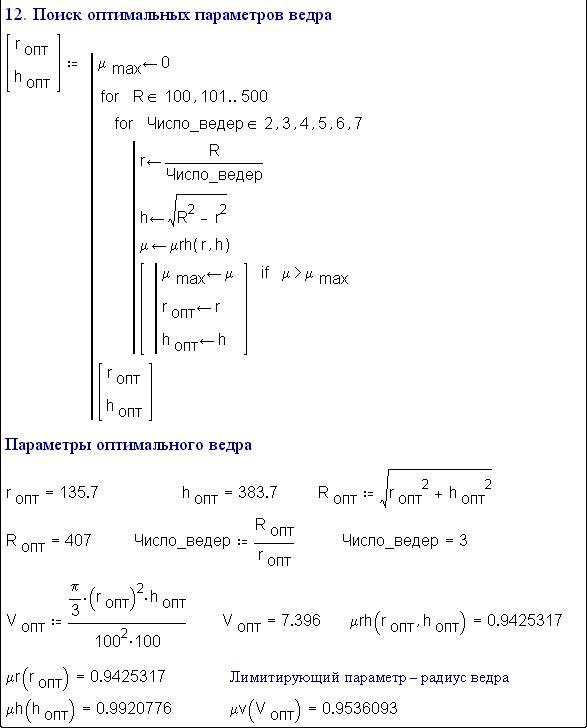
Fig. 6.41. Optimum radius of fire bucket

Step 1 (fig. 6.41). The matrix μ_r stores people's views about the optimum (most convenient) base radius r of a conical fire bucket, expressed in millimeters. This data could be gathered by making buckets of various geometries, giving them to people to try out, and then asking for estimates on a scale:

· convenient (1);

· more convenient than inconvenient (0.67);

· more inconvenient than convenient (0.34);

· inconvenient (0).

It would be possible to have more options within the range 0-1. In step 1 we have a limited familty of points, but these also could be increased; there are as many opinions as people. Readers can ask all their friends, and add new columns to the matrix [μ_r]

Step 2. The survey data is processed by the least squares method (see Etude 4). We can see that the data approximately fits a normal distribution curve (see figs. 6.41 and 6.42). The idea of a 'membership function' μr for the radius of the bucket is one of the basic concepts of FST. In normal mathematics it would be considered that a certain size either belongs, or does not belong, to a particular set; in FST it's permissible to say that the size belongs to the set to some extent (so many percent).

Step 3. The statistical processing is completed and plotted.

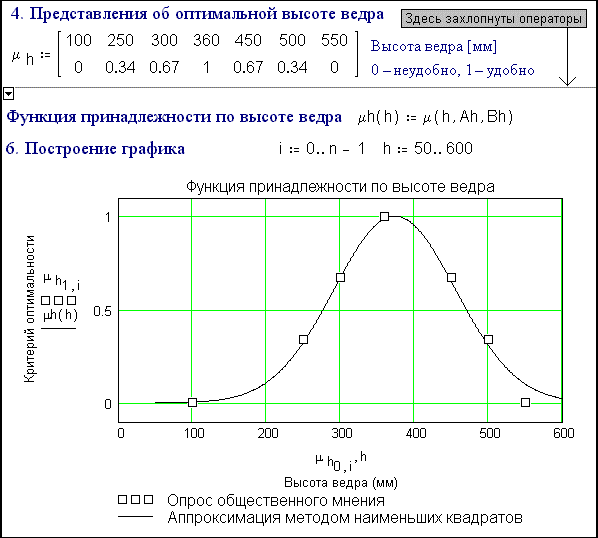
Fig. 6.42. Optimum height of a fire bucket

Steps 4-6 (fig. 6.42) repeat steps 1-3, but for a second parameter of the bucket, its height.

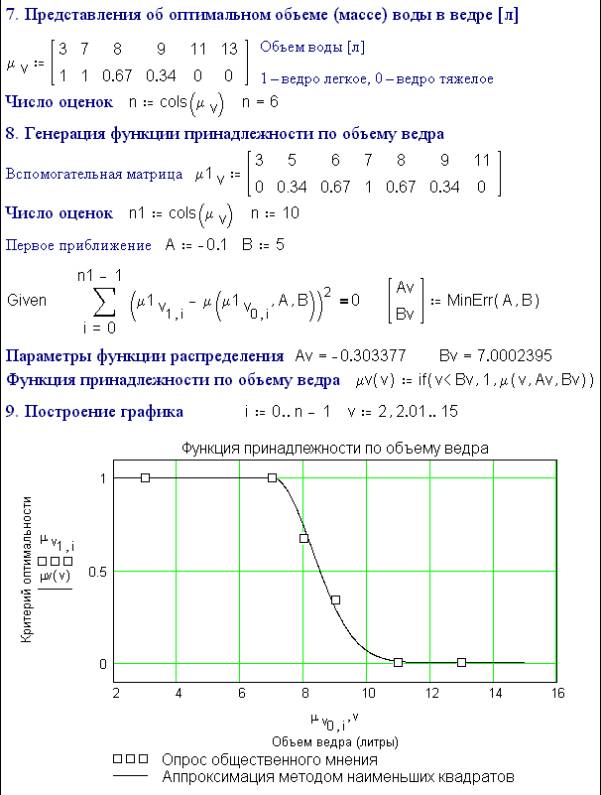
Fig. 6.43. Optimum volume of a fire bucket

Steps 7-9 repeat steps 1-3 and 1-6 for the third important parameter of the bucket, its volume (or weight – they're proportional). This is based on human estimates:

· bucket is light (1);

· bucket is more light than heavy (0.67);

· bucket is more heavy than light (0.34):

· bucket is heavy (0).

The survey data is processed as before, but using a "one-sided" cumulative distribution curve (see item 9 in a fig 6.43). (When designing technical systems, such parameters wouldn't be based on a survey but on figures provided by experts to the decision-makers).

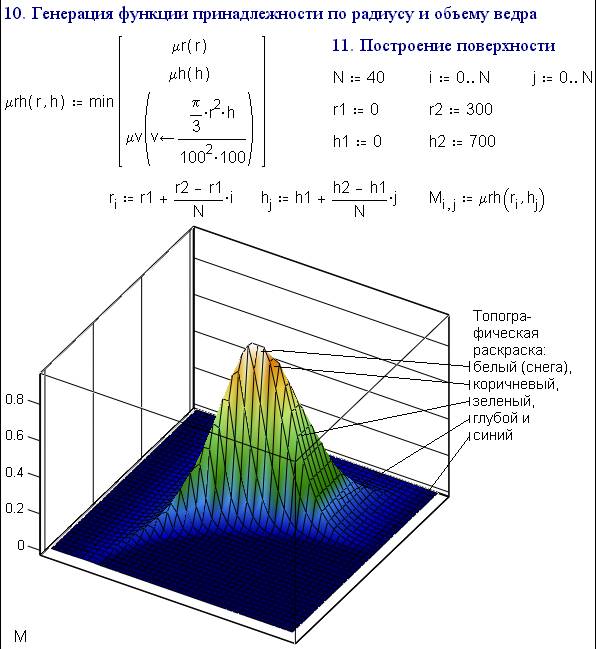
Fig. 6.44. the "Rotated" optimum fire bucket

Step 10 in fig. 6.44 is the nucleus of the solution of our: in this, a two-parameter membership function is generated by the merging (akin to multiplication) of two single-parameter membership functions.

In FST there are no traditional concepts of addition, subtraction, multiplication etc.(those represented by the mathematical operators "+", "-", "×" etc. in the Mathcad environment). In FST, multiplication (crossing of sets – logical AND) is replaced with an operation of searching for a minimum; and addition (merging of sets – logical OR) by searching for a maximum. The mathematics of precise sets is a special case (a subset of the mathematics of fuzzy sets) where these operators/functions are genuinely equivalent. This means that in the Mathcad environment, where there are no built- in AND and OR operators, we can create equivalents using the min and max functions we described in Etude 3.

In our task the membership function mu_rh is generated by the fuzzy addition (min) of the functions mu_r, mu_h and mu_v. That is, the fuzzy set "the convenient bucket " is the intersection of three other fuzzy sets: "convenient radius of bucket" (step 1), "convenient height of bucket" (step 6) and "a not heavy bucket" (step 9).

Step 11. The top of the 'mountain' – the surface plot of function mu_rh – is the point where the parameters of most convenient fire bucket lie.

Fig. 6.45. Designing the optimum fire bucket

Step 12 (fig. 6.45). Searching for the maximum of the function mu_rh in the Mathcad environment can be done in various ways (see Etudes 2 and 3). We'll proceed this way: we'll imagine metal disks of various radius R (from 10mm-500 mm with a step of 1 mm) and cut each size into 2 to 10 identical buckets. This gives a large variety of bucket sizes and geometries, and we'll consider the optimum (the most convenient) bucket to be the one for which the membership function mu_rh is maximised.

Even the reader who hasn't been paying much attention will notice some discrepancies and simpiflications in our analysis of this task. Three of them are:

· Unlike our theoretical bucket, a real one is never filled up right to the brim ("what counts as full?" defines another fuzzy set).

· The author has only loosely defined, and often confused, such concepts as "volume", "weight", and "weight of bucket".

· We haven't taken into account the weight of an empty bucket, and also the material from which it is made.

However it is merely necessary to glance again at the diagrams illustrating fuzzy sets in figs. 6.41, 6.42 and 6.43 to understand a major virtue of applying FST to decision-making tasks. Our solution works in isolation, so it's possible to express the essence of a task disregarding various minor variables: the density of water, weight of the empty bucket, degree of filling, etc. This feature is now realized, for example, in automatic control systems, where regulators based on FST rules are more 'attentive' to the basic signal and less susceptible to noise. It turns out, though it seems paradoxical, that the traditional 'precise' control algorithms qualitatively lose out to 'fuzzy' ones, or are their special cases. In the field of automatic control theory, a certain stagnation could be seen until recently, as any new algorithms couldn't be compared to the older Proportional Integral Derivative (PID) control algorithm. The principles of PID control can be seen in the procedure for a bank's credit check on a client applying for a loan. The banker, in assessing the decision, considers:

1) The sum of money in the client's account (this is the proportional component: the richer the client, the larger the loan that can be offered);

2) The average sum in the account over, say, the last five years (the integrated component; checking this ensures that the client didn't borrow a million pounds the day before, to create the illusion of solvency); and

3) The rate of change of the account (the differential component, showing whether the client's business is on the rise or decline);

It's possible to take into account other factors, but three is a nice number!

The PID-control algorithm has imperceptibly become something of a fetish. Fuzzy management cames as a fresh breeze in the theory of automatic control, whose basic rules are now open to review. To be sure, there are other opinions. Some scientists believe that the use of FST in automatic control, and cybernetics in general, is just replacing one uncertainty with another ("trying to stitch soapsuds", the Russian expression goes) and that's all there is to it. Sceptics explain away the observed improvement in control quality to our devoting more attention to regulator technology (as if the ritual of attention could improve performance). Besides some researchers believe that FST, since it dates back 30 years (it was devised by the Iranian-American Dr Lotfi Zadeh at UC/Berkeley in the 1960s) is old and best forgotten.

Actually, the skip from a task about a tripartite duel to one about an optimum bucket wasn't entirely casual. Traditionally, precise sets are illustrated by circles with sharply delineated borders. Fuzzy sets are drawn as circles formed of separate dots, with a high density at the centre and thinning to zero (as if evaporating) towards the edges. Such 'fuzzy set' images can be seen on a firing range wall where targets are hung. The bullet traces form a probability distribution, whose mathematics is well-known. It appears that the theory for working on fuzzy sets, as probabilistic distributions, has already existed for a long time...

We keep talking about fuzzy sets. But are they – mathematically – actually sets? To be consistent, it's necessary to ascertain that the fuzzy set has elements (fuzzy subsets, fuzzy sub-subsets, etc). We'll return to a classical example: a heap of grain. An element of this fuzzy set will be, say, a million grains. But a million grains is not a precise element: it's a fuzzy subset. If you count out grains, whether manually or automatically), it's no wonder that you might mistake, say, 999 997 grains for a million. In FST terminology, you could say that the element 999 997 has a 'membership value' 0.999997 for the fuzzy set {a million grains}. Besides, even "a grain" is not a precise element, and is another fuzzy subset: it might be a high-grade grain, but there are also underdeveloped grains, grain fragments, and bits of husk. Depending which way you decide, you might count one grain as two, or vice versa.

The fuzzy set isn't very easily accommodated in the digital computer with classical data constructs: elements of a file (a vector) should be new files of files (composed of vectors and matrices, in the case of Mathcad). The classical mathematics of precise sets (number theory, arithmetic, etc) is rather like a hook, with the help of which we anchor ourselves on the slippery and fuzzy environmental world. And a hook is a rough implement, quite often damaging what it's embedded in. The terms describing fuzzy set membership values (there are plenty in this book and others – "much", "some", "a few", and so on) are difficult to make into programming statements because they're contextually dependent. It's one business to say, "Give me a few sunflower seeds" to someone with a cupful, and another to say the same to a driver hauling a lorryload.

Whether it is possible to see a certain crisis in theory and practice of programming connected with contradict between precise structure of the programs (data) and fuzzy world? Is it necessary to develop fuzzy programming languages for implementation fuzzy algorithms that accommodate fuzzy data? Opinions vary. In the author's view, programmers (and they have the last word) have learned poorly how to cram the fuzzy world into the strictly determined computer. Figs. 6.41, 6.42, 6.43, 6.44 and 6.45 are an example.

6.10. A and B sat on a pipe

We can imagine A and B sitting down to pass the time of day – in our case, not on a simple pipe, but on a fire bucket. We'll now explain the 'universal' meaning of these parametrical factors A and B (more correctly A_r, B_r, A_h, B_h, A_v and B_v) included in the approximation expressions of stages 2, 5 and 8 (fig. 6.41-43).

Viewing the fuzzy set as a statistical distribution, A represents the 'spread' of the distribution, and B the parameter value giving the peak of the distribution. Imagine we carry out a global statistical experiment. We measure for all adult humans some parameter – weight, height, intelligence, etc – whether represented numerically or estimated by some criterion (genius, talented, very clever, simply clever... down to idiot). The data points we shall transform into a curve (see sections 1-3 in figures 6.41, 6.42 and 6.43) where the X-axis is the measured human parameter, and the Y-axis the percentage of people with a given value of that parameter. We carry out this statistical exercise separately for men (M) and women (F). What do we get?

Case 1: A_M = A_F, but B_M > B_F:

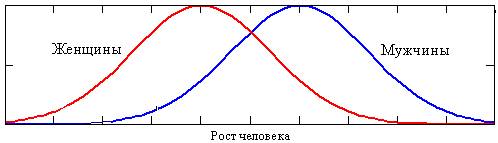
Curves turn out like this for parameters – such as height, weight, strength of muscles, etc – pertaining particularly to men rather than women. This is related to evolution: sexual dimorphism is related to the general trend in species size. If the male body is larger than the female, the next generation tends to be larger. With spiders, for example, the male is much smaller than the female, and so – thank God – spiders are smaller now than the geological past.

Case 2: A_M < A_F, but B_M = B_F:

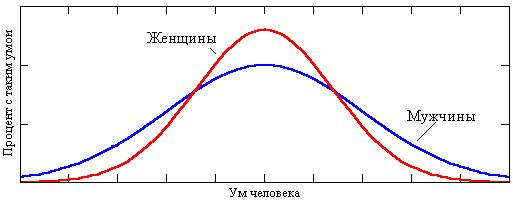
The curve looks like this for a parameter – intelligence – whose importance applies equally to both sexes, and has not varied for millennia. Many consider it quite proven, that if modern humans were suddenly stripped of education and culture, we would be no more intelligent (maybe even less so) than the Ancient Greeks. It's not known why, but there is a greater spread for men: there are more men of genius (Nobel prizewinners, inventors, writers and artists – at the right edge of the diagram) only because there are also more men of extremely subnormal intelligence (the left edge). The average woman is cleverer the average man: the centre of the "female" distribution is raised at the expense of a smaller spread. The areas of both curves is, however, identical: no offence intended to anyone, but we believe that the Lord God or Nature (whichever you believe in) has shown consideration in distributing intelligence equally to both halves of humanity.

We can try to apply the theory of fuzzy sets, as described in Etude 3, to the problem of computer piracy. The law divides all people into two precise sets: {legal users of programs} and {illegal users – pirates}. In real life, it's much more complex: computer users fall into two fuzzy sets, with a great variety of motives. At one extreme are people trading 'black' disks at Gorbushka (the left-hand axis of the diagram above); at the other are those who work only with legal copies and have never broken any license agreement (the right-hand axis). Again, it's possible to construct a humpbacked statistical curve, this time above an axis "sinner ... saint" describing the condition of the computer market in a particular country. Where does the maximum of this curve lie, and how is it shifting with time?