6.8. The problem of a
label
(A part from the book “Mathcad 8 Pro for Students and Engineers”)
Valery Ochkov http://twt.mpei.ac.ru/ochkov
(Translation into English by R.Girvin)
This problem of a label – or more correctly, problem of disposing with a
label -– we'll look at in solving an ancient English puzzle about fishermen and
fish:
"Three fishermen
lay down to sleep, not having counted or divided their catch. In the night, one
of them woke up, and (not quite trusting the others) decided to divide the pile
of fish and take his share. But the number of fish wasn't visible by three.
However, he found he could throw one fish away, then take exactly a third. This
he did (noting, in the true spirit of fairness, that an even number of fish was
left for his comrades) and went back to sleep. Later, the second and third
fishermen woke in turn, and each went through the same process. The question
is, what is the minimum number of fish in the catch that fulfils these
conditions?"
The reader might like first to try to solve
this task by hand; but we'll involve the computer in this for two reasons.
Firstly, it lets us consider some ways to structuralize programs in the Mathcad
environment: methods of clearing programs of labels, and 'squeezing' them into
the rigorous framework of structural design. Secondly, we'll show that the
Fishermen's Problem has, until now, been solved incorrectly...
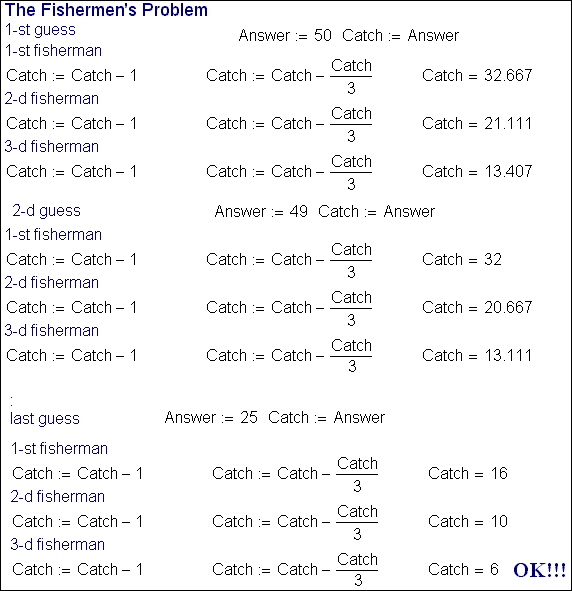
Fig.
6.22. The Fishermen's Problem: 'unprogrammed' Mathcad solution (6_21_fisherman.mcd)
This problem can be solved in Mathcad without
resorting to programming. Fig. 6.22 shows how this
might be done how by successive manual approximations, with Mathcad just
automating the division procedure. We set a first guess at 50 fish and see if
the division works; if not, we try 49; and so on, decrementing the guess by one
if the division produces a non-integer at any stage. Eventually, we guess at 25
fish, and this proves to be a solution. The first fisherman throws away a fish,
and takes eight, leaving 16 (eight each for the others, he thinks). The second
(not knowing what the first has done) leaves ten; and the third, six.
This solves the task – but by applying 'manual'
work in setting the value of the variable Catch and
decrementing the value of the variable Answer.
(Note that duplicating the block of operators fixing the actions of the three
fishermen, though done for clarity in Fig 6.22, isn't necessary.
It's sufficient to decrement Answer
and keep track of Catch).
Let's try to automate the search for a solution
to this task.
'1 Initial unstructured BASIC program
Input "Guess";
Answer
label:
Catch = Answer
For Fisherman = 1 To 3
Catch = Catch – 1
Catch = Catch - Catch /
3
If Catch > Int(Catch)
Then Answer = Answer - 1: Goto label
Next
Print
"Answer "; Answer; “fish”
'2. First stage of structuralization: a start
Input
"Guess"; Answer
Answer =
Answer + 1 ‘ step backward
label: Answer
= Answer - 1 ‘ step forward
Catch = Answer
For
Fisherman = 1 To 3
Catch = Catch – 1
Catch = Catch - Catch /
3
If Catch > Int(Catch)
Goto label
Next
Print
"Answer "; Answer; “fish”
'3. Second stage of structuralization: addition of an
attribute
Input
"Guess"; Answer
Answer =
Answer + 1
label:
Answer = Answer – 1
Catch =
Answer
Divided = "yes" ’
indicates catch divided
For
Fisherman = 1 To 3
Catch = Catch – 1
Catch = Catch - Catch /
3
If Catch > Int(Catch)
Then Divided = “no”
Next
If Divided =
“no" Goto label
Print
"Answer "; Answer; “fish”
4. Third step of structuralization: disposal of the
label
Input
"Guess"; Answer
Answer =
Answer + 1
Do ’ start loop
with checking on exit
Answer = Answer – 1
Catch = Answer
Divided = "yes"
For
Fisherman = 1 To 3
Catch = Catch – 1
Catch = Catch - Catch /
3
If Catch > Int(Catch)
Then Divided = “no”
Next
Loop Until Divided = "yes" ’ end loop
Print
"Answer "; Answer; “fish”
Fig.
6.23. BASIC programs for solving the Fishermen's Problem
Fig. 6.23 shows four
BASIC programs to automate the solution of the Fishermen's Problem. In all
four, the operator Input requests the first guess (50 fish, for example) and the operator Print gives out the answer: 25 fish.
The first program follows exactly our 'manual'
algorithm. Inside the loop for the three fishermen's successive leavings, we
watch until we find fractional 'tails': that is, the parameter Catch is not an integer (the built-in
BASIC function Int chops off these
tails; the Mathcad analogue is the floor
function). Then the guess decrements by one (Answer = Answer - 1) and the program control passes to the labelled
statement (Goto label).
Before this program can be translated to
Mathcad's programming language, we need to get rid of the label. And not only
because in Mathcad's programming arsenal there is no facility to jump to a
label, either conditionally or unconditionally, but for other reasons
unconnected with Mathcad. In our 'toy' program (item 1 in a Fig.
6.23) the label is quite pertinent and natural, but if a program with
labels expands, it becomes difficult to understand and practically impossible
to debug and develop. The result, as structural programming wizards rightly
emphasise, becomes like spaghetti: try pulling out a block of statements for
separate debugging or compilation, and you find adhering strings of Goto links. Besides, such program can't
be created by a group of developers ('bottom-up' technology). The first implementations
of the Pascal language had no labels at all, as Pascal was developed by Niklaus
Wirth for training students in structural programming. The label has appeared
only in the late versions. So I think our view on learner programmers and the
label must be, "Hide matches from children"!
The first step in structuralizing the BASIC
program (see item 2 in Fig. 6.23) is moving the
decrement code from the conditional statement to the label. That is:
If Catch > Int (Catch) Then Answer = Answer - 1: Goto
label
becomes
label:
Answer = Answer - 1
...
If Catch > Int(Catch) Goto label
There is another necessary change. Rather like
an athlete taking a step back before a jump, we must insert Answer = Answer
+ 1, because when
the program is run, label begins by decrementing Answer. Structuralizing generally
complicates the algorithm a little: remember that "There's no such thing
as a free lunch", "Beauty is only achieved by suffering", and so
on.
The second step in structuralizing (see item 3)
is extracting the conditional jump from the body of the For loop. For this purpose, we
introduce an auxiliary binary variable, Divided, indicating successful or unsuccessful division. Inside the loop, the
conditional jump to label is replaced by an "alternative with one shoulder" (that is, Divided stores the result of the binary
choice, carrying it to a single exit from the loop – one of the basic
structural managing designs). The conditional jump 'slips' down and outside the
loop.
After this (see item 4) the program can be
modified with one more basic of structural design: a loop with checking on
exit, which performs the same function as label and If ... Goto label in item 3. This finally enables the program to completely dispense with
labels: the outer loop with exit checking, containing an inner For loop with its 'alternative with one
shoulder'.
After all these manipulations, the fourth
variant of the BASIC program is the one possible to copy to Mathcad (see Fig. 6.24). It's necessary to define it as a user
function, as there are no Input and Print operators in the Mathcad language. Their analogues (the operators [ ]:= [ ] and [ ]=) work, alas, only outside of
programs.
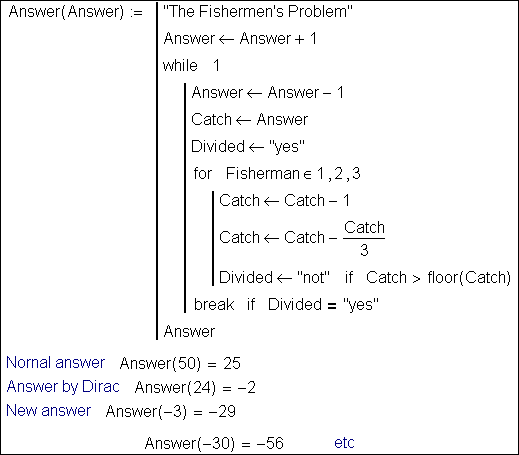
Fig.
6.24. Mathcad program for solving the Fishermen's Problem (6_22_fisherman.mcd)
In Fig. 6.24 the result
of calling the function Answer are shown for various input values: 50, 24, -3 and even -30 fish. The
English physicist and early quantum theorist Paul Dirac postulated not only
antiparticles but "antifish". In one version of a well-known story[1],
he is remembered as saying that 25 fish was an incorrect solution to this
problem, and that the correct answer is -2 fish (or two antifish). If we start
with two antifish, throwing away one away gives three antifish; we take our
share of one antifish, leaving two antifish .. and so on indefinitely. Our computer
solution of the problem shows that even Dirac was mistaken: "Paul, you are
not right!" The conditions of the problem are fulfilled by an infinity of
numbers – we'll call it a Dirac of fish – with a step of 27 (i.e. -2, 25, 52,
etc).
To avoid being an ultra-pedant[2],
it's possible to insert at the end of the for loop in Fig. 6.24 a statement break if
Divided = "no" to interrupt the loop's operation even before
all the fishermen have taken their share. If there aren't three fishermen but
more (for example, thirty-three – a task for the reader), this device
essentially speeds up the program's operation (see the heading
"Optimization of Mathcad programs"). The task can be complicated even
more, generalizing to any number of fisherman sharing, or discarding, any
number of fish.
The Fishermen's Problem can be solved in
another way, by reversing it. Rather than making an initial guess for the
catch, we can assume that the last fisherman leaves two fish (it can't be
fewer) and increment that number by one until the conditions of the task can be
fulfilled. This will solve the problem faster, and we won't ever get solutions
of -2 or -29 fish (the paradigm "Keep it
simple, stupid!" applies here). It's psychologically difficult for humans
to appreciate negative solutions, but the machine does it quietly, without any
prejudices. A more thought-out analytical solution of this task – the search
for integer roots of one equation with two unknowns – doesn't give the negative
answer.