Интерполяция,
экстраполяция и сглаживание
или
Ложь, наглая ложь и статистика[1]
В.Ф. Очков, Е.П. Богомолова
Сначала дадим
расшифровку некоторых терминов, которые помогут нам понять суть проблемы,
поднимаемой в статье [1].
Функция (от лат. functio – исполнение,
осуществление) – это закон f, по которому каждому элементу x
из одного числового множества ставится в соответствие некоторый определенный
элемент y из другого числового множества,
так что y=f(x).
Корреляция (от лат. correlatio – соотношение) – вероятностная
или статистическая зависимость, не имеющая строго функционального характера (см.
выше) из-за невозможности точно учесть влияние множества одновременно
меняющихся факторов.
Интерполяция (от лат. interpolation – изменение, переделка) – приближенное
или точное нахождение какой-либо величины по известным отдельным значениям этой
величины, т.е. восстановление (точное или приближенное) функции (см. выше) по
ее нескольким известным значениям.
Регрессия (от лат. regressio – обратное движение) – такая зависимость
среднего значения какой-либо величины от некоторой другой величины или от
нескольких величин, что одному и тому же значению независимой переменной x
могут соответствовать в зависимости от случая различные значения величины y.
А теперь к делу.
При обработке
экспериментальных данных мы обычно сталкиваемся с двумя принципиально разными
случаями: или полученные данные связаны некоторой функциональной зависимостью
(формула которой нам неизвестна), или таковой функциональной зависимости не
существует, хотя и наблюдается корреляция.
Но есть и третий
вариант: две величины действительно связаны функциональной зависимостью, и
теоретически каждому значению аргумента x
соответствует ровно одно значение y. Но при проведении эксперимента
не удается получить значения с достаточной степенью точности, и
экспериментальные результаты представляются в виде таблиц значений (xi, yi), yi = f(xi) ± εi, где εi – погрешности измерений. Если в
этом случае просто соединить экспериментальные точки отрезками прямых, то
получится ломаная, не имеющая ничего общего с той функциональной зависимостью,
которая реально существует. Причем форма этой ломаной из-за ошибок измерений
при повторном эксперименте не воспроизводится.
В первом из
рассмотренных случаев для получения приближенной формулы зависимости двух
величин применяют интерполяцию. Во втором и третьем – регрессивный анализ.
Приведем примеры.
Студентам, решающим
задачи по физике, химии и другим учебным дисциплинам, часто приходится
заглядывать в справочники, где некая функциональная зависимость представлена в
виде таблицы: теплопроводность какого-либо металла в зависимости от
температуры, плотность водного раствора какой-либо соли при фиксированной
концентрации зависит от той же температуры и т.д. и т.п.[2]. В этих
таблицах пары чисел «температура-свойство» показаны лишь для некоторых значений
температуры, например, 0, 10, 20, 30 и т.д. градусов по шкале Цельсия. А значение
свойства (теплопроводности металла или плотности раствора) нужно, допустим,
взять при 17 °С. Подразумевается, что величины, указанные в таблицах,
являются точными (правильнее сказать, получены с достаточной степенью
точности). Поскольку физические законы позволяют считать рассматриваемые
величины функционально зависимыми, то применяют интерполяцию. Простейшую –
линейную или более сложную – интерполяцию многочленами либо сплайнами. При
линейной интерполяции мы мысленно, на бумаге или на дисплее компьютера фиксируем
две точки, проводим через них прямую линию и по ней находим нужное
промежуточное значение. При нелинейной интерполяции отыскивается обладающая
определенной гладкостью функция, график которой проходит через указанные точки
(интерполяционные узлы).
В случае отсутствия
каких-либо определенных функциональных связей между двумя экспериментальными
величинами интерполяция может привести к ложному результату.
Когда-то перед
лекцией на тему «Регрессионный анализ» по курсу «Информационные технологии» первый
автор статьи подбирал пример статистической выборки для такого анализа. Но
когда он «взошел на кафедру» и взглянул на аудиторию (рис. 1), то он понял, что
эта выборка находится прямо перед его глазами. Была проведена перекличка
студентов. Юноши при вызове их по фамилии вставали и сообщали свой вес[3] и рост (студентки естественно, были
исключены из этой процедуры). Данные заносились в два вектора с именами Вес
и Рост в среде математической программы
Mathcad (скачать Mathcad
15 файл с этими данными >>>). В векторах получилось по 50
элементов. Эти массивы чисел послужили хорошей затравкой для лекции.

Рис. 1. Студенты –
"подопытные статистические кролики" (правая половина аудитории: часть
выборки)
Линейная
интерполяция, формально примененная к паре величин «Рост – Вес», показана на рис.
2. Были взяты данные двух студентов («маленький студент» и «большой студент») и
через соответствующие точки (узлы интерполяции) была проведена прямая линия на
плоскости. Были также определены параметры этой прямой – коэффициенты a и b уравнения y = a + b x.
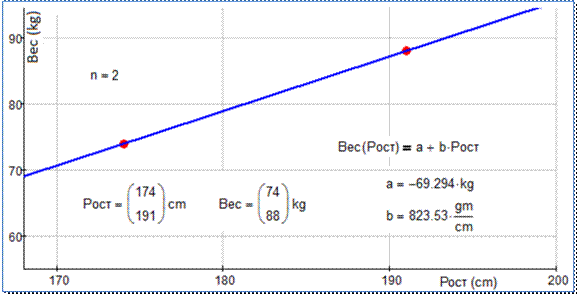
Рис. 2. Линейная интерполяция по
двум студентам, пардон, точкам
Как
рассчитывались коэффициенты a
и b, показано на рис. 3. Можно в
справочниках поискать соответствующие формулы, а можно в среде Mathcad решить пару линейных уравнений
(рис. 3) и получить ответ.
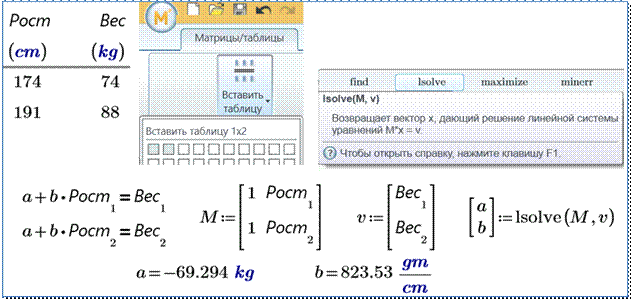
Рис. 3. Численное решение системы
линейных уравнений прямой, проходящей через две точки на плоскости
На
рисунке 3 в таблицу вводятся вес и рост "маленького и большого студентов",
затем записывается система двух линейных алгебраических уравнений прохождения
прямой через две точки, формируется квадратная матрица M коэффициентов при неизвестных a и b и вектор свободных членов v. Решение системы найдено с
помощью встроенной в Mathcad
функции lsolve.
Нашу систему двух линейных уравнений можно решить и аналитически (рис. 4),
получив формулу для определения коэффициентов a и b, входящих в уравнение прямой
линии, проходящей через две заданные точки с координатами на плоскости x1-y1и x2-y2.

Рис. 4. Символьное решение
системы линейных уравнений прямой, проходящей через две тоски на плоскости
Тут мы намерено
смешали интерполяцию (проведение линии через точки) с аппроксимацией (проведение
линии вблизи точек). Если выбирать пару студентов случайным образом, то наша
прямая линия может быть различными способами ориентирована на плоскости «Рост –
Вес», поэтому доверия к такому способу описания зависимости величин в этом
случае нет. Линейная интерполяция тут не
годится: она еще раз «льет воду на мельницу» тех, кто в шутку или всерьез
утверждает, что есть «ложь, наглая ложь и… статистика». На график, показанный
на рис. 2, нужно «высыпать» все 50 точек со статистическими данными студентов и
постараться как-то провести прямую линию, отображающую взаимозависимость
(корреляцию) роста и веса человека, не противоречащую основным тенденциям
поведения измеренных величин – см. рис. 5.
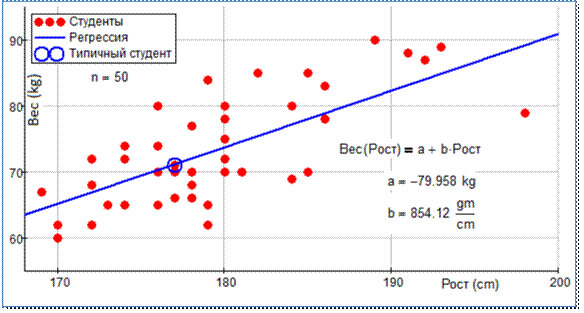
Рис. 5. Линейное сглаживание
(аппроксимация)
Когда-то давно в докалькуляторную и докомпьютерную
эру такая работа делалась примерно так: на миллиметровой бумаге в определенном
масштабе проставлялись точки исходных статистических данных, а затем с помощью
прозрачной линейки выставлялась некая прямая линия, наилучшим (оптимальным)
образом описывающая связь роста человека и его веса. При этом каждый проводящий
такую линию мог руководствоваться какими-то своими субъективными понятиями об
оптимальности положения этой прямой на плоскости, то есть о значениях
коэффициентов а и b, задающих уравнение прямой линии у = а + b∙х (константы а и b,
кстати, рассчитаны и прописаны на рис. 2 и 5). На компьютере эту работу можно
автоматизировать, если выбрать какой-то объективный критерий оптимизации. Одним
из таких критериев является критерий минимума суммы квадратов «вертикальных»
отклонений точек от кривой (в нашем случае от прямой линии). Сам же метод
такого расчета называется методом
наименьших квадратов: МНК. Если возникнет спор о том, чья прямая линия,
проведенная в массиве точек, более правильная, то можно циркулем и линейкой
замерить отклонения по вертикали точек от прямой, возвести каждое такое
отклонение в квадрат, просуммировать эти квадраты и сравнить полученные суммы.
У кого эта сумма окажется меньше, у того и прямая линия правильнее иллюстрирует
исследуемую статистическую зависимость. Если у нас есть только две точки (рис.
2), или точек больше двух, но все они лежат на одной прямой, то, очевидно,
сумма квадратов отклонений будет равна нулю. Но если же не все точки лежат на одной
прямой (рис. 5), то можно предположить, что есть такое положение сглаживающей
прямой (такие значения коэффициентов а и b), при
котором сумма квадратов отклонений будет минимальной.
На рис. 6 показан Mathcad-документ,
решающий эту задачу оптимизации.
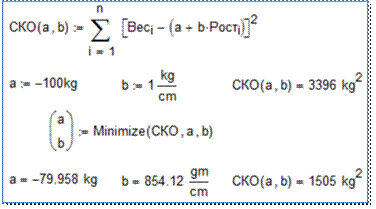
Рис. 6. Метод наименьших
квадратов как задача оптимизации
В
Mathcad-документе,
показанном на рис. 6, формируется функция пользователя с именем СКО
(сумма квадратов отклонений масс студентов – целевая функция оптимизации),
имеющая два аргумента – а и b. Далее задаются начальные
значения этих переменных оптимизации с опорой на известную эмпирическую
формулу, гласящую, что рост взрослого человека в сантиметрах – это его вес в
килограммах плюс сто. Наша задача – проверить эту гипотезу на данной статистической выборке – на 50
студентах. Затем в расчете на рис. 6 вызывается встроенная в Mathcad функция Minimize,
которая начинает менять заданные нами значения переменных а
и b
так, чтобы функция СКО приняла минимальное значение.
Как это делается – это отдельный разговор. Мы же видим, что при начальных
значениях коэффициентов (переменных) а и b функция
СКО возвращала значение 3396 kg2, а при оптимальных значениях –
1505 kg2, и верим
что меньшего значения в пределах заданной точности найти не удаться. На рис. 5
можно видеть эти оптимальные значения коэффициентов а и b и
«оптимальную» прямую линию, «пронизывающую» массив точек. К оптимальности этого
решения мы еще вернемся ниже.
Задачу,
сформулированную на рис. 6, можно решить и аналитически, если вспомнить, что у
функции двух аргументов в точке минимума частные производные по обеим
переменным равны нулю. На рисунке 7 показано символьное решение системы двух
уравнений равенства нулю частных производных функции СКО(a, b) по аргументам a и b.

Рис. 7. Символьное решение задачи
оптимизации – поиска минимума функции двух аргументов
У
функции СКО суммируются квадраты «вертикальных»[4] отклонений
точки от прямой линии. И это понятно: если убрать квадрат, то суммирование
приведет к некорректной постановке задачи: будут суммироваться отклонения с
разными знаками. А можно ли возведение в квадрат заменить взятием абсолютного
значения? Для этого достаточно внести соответствующее изменение в первый
оператор расчета, показанного на рис. 6. Но в этом случае функция Minimize будет иметь плохую сходимость и
выдавать совершенно разные ответы при разных начальных значениях переменных a
и b.
Дело в том, что функция абсолютного значения угловатая, если так можно
выразится. А природа не любит острых углов. Кроме того, стоит взглянуть на рис.
8, где сделана неудачная попытка аналитического решения системы двух уравнений
– равенство нулю частных производных не от функции СКО(a, b),
а от функции СМО(a, b):
Сумма Модулей Отклонений.

Рис. 8. Неудачное решение системы
двух уравнений
На сайте http://www.math.wpi.edu/Course_Materials/SAS/lablets/7.3/7.3c/index.html
можно видеть описание и сравнение методов наименьших квадратов и наименьших
модулей.
Одна точка на рис. 5
обведена кружочком – это, можно сказать, некий типичный студент, отклонение
веса которого от средней линии минимально.
В связи с этим
возникает интересное предложение по подведению итогов различных конкурсов
красоты. Сейчас в них слишком много субъективности, а значит – обид, слез и
даже судебных тяжб. В финалы таких конкурсов обычно попадают
«красавицы-раскрасавицы» (см., например, рис. 1), из которых довольно трудно
выбрать самую оптимальную, пардон, самую красивую мисс или миссис. Так вот,
можно у этих финалисток замерить вес и рост или другие размеры (пресловутые
90-60-90, например), провести через точки линию и назвать победительницу так,
как это показано кружочком на рис. 5.
Но вернемся к нашим
более серьезным делам. Встроенная в Mathcad функция Minimize,
показанная на рис. 6, позволяет нам реализовать метод наименьших квадратов в
его общей постановке: пользовательская (целевая) функция с именем СКО в
принципе может иметь любое число аргументов, а ее правая часть – любую
функциональную зависимость для сглаживания точек. Но для частных случаев в
среде Mathcad
есть более простые инструменты решения задачи статистической обработки данных
методом наименьших квадратов. Так, на рисунке 9 показан вызов
двух встроенных в Mathcad
функций intercept
и slope, возвращающих
значение коэффициентов а и b сглаживающей прямой у
= а + b∙х. В эти две функции заложены формулы,
выведенные нами на рис. 7. Они также использованы в расчете на рис. 9.
Кроме того, на рис. 9 показана работа еще одной функции, возвращающей
коэффициенты линейной регрессии, – функции line. Английские слова an intercept и aslope можно перевести как
«пересечение» и «наклон»: значение коэффициента а – это
значение абсциссы при пересечении нашей прямой оси Y, а значение константы b – это
тангенс угла наклона прямой к оси Х. Вернее так. Про тангенс и угол можно было
бы упомянуть, если б наши исходные векторы были бы безразмерными. При размерных
векторах (масса и длина, как в нашей задаче) это просто некий наклон –
отношение приращения по вертикали (граммы) к приращению по горизонтали
(сантиметры).

Рис. 9. Инструменты пакета Mathcadдля решения линейной
регрессионной задачи методом наименьших квадратов
Через точки,
показанные на рис. 5, можно провести только прямую линию. Но если исследователь
видит в исходных разбросанных точках не прямую, а, например, параболу или
полином более высокой степени с коэффициентами a, b,
c, d и т.д., то он может вызвать Mathcad-функцию regress, у
которой уже не два (см. рис. 9), а три аргумента: вектор ординат точек, вектор
абсцисс точек и степень полинома: 1 (наш случай, показанный на рис. 5, 7, 8 и
9), 2 (парабола), 3 (полином третьей степени), 4 – четвертой (см. рис. 10 ниже)
и т.д. до того момента, когда степень полинома станет равна числу точек минус
единица. В этом случае аппроксимация (проведение кривой вблизи точек) перейдет
в интерполяцию (проведение кривой через точки). Но тут не так все просто.
Авторская анимация на
сайте http://communities.ptc.com/videos/1473 (рис. 10) показывает, как
меняется форма аппроксимирующей кривой вблизи 15 точек и как добавляются новые
коэффициенты ki при изменении степени полинома от
1до 14.
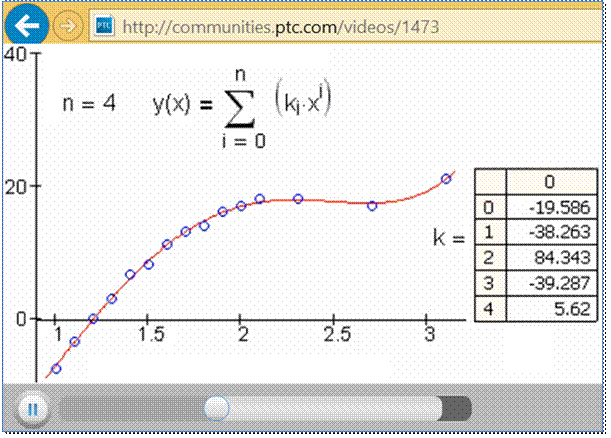
Рис. 10. Кадр анимация работы
функции regress: через 15 точек проводится линия полинома 4-й
степени
При приближении
значения степени регрессионного полинома к значению числа заданных точек (рис.
11) может наблюдаться, так называемая, осцилляция (лат. ōscillātio
качание, раскачивание). Видно, как кривая регрессии приближается к точкам (при
n = 14 аппроксимация переходит в интерполяцию), но при этом в
промежутках между точками кривая может «раскачиваться» — далеко уходить от
точек, сводя на нет всю интерполяцию и аппроксимацию.
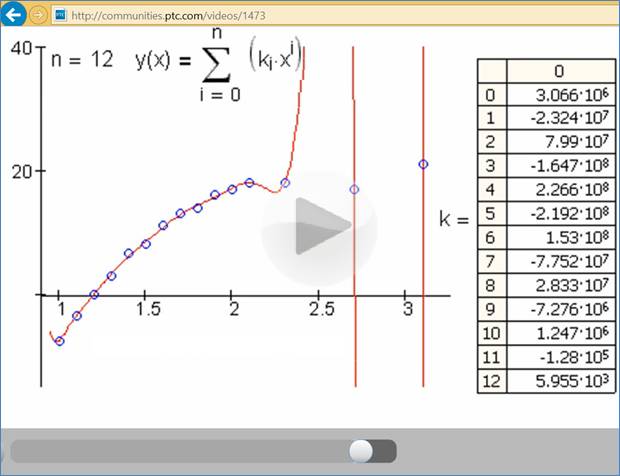
Рис. 11. Кадр анимация работы
функции regress: через 15 точек проводится линия (часть ее
обрезана) полинома 12-й степени
Между двумя правыми
точками на рис. 11 из-за осцилляции мы видим не «статистику» и не просто
«ложь», а «наглую ложь».
Но вернемся к
терминам, описанными нами в самом начале статьи. Взаимозависимость роста и веса
человека – это типичный пример корреляции,
а наш поиск значений коэффициентов а
и b линейной функции – типичный пример регрессионного
анализа.
В классической
математике, как правило, мы имеем дело не с корреляцией, а с четкими
функциональными зависимостями. Каждому значению плоского угла, например,
соответствует четкое значение синуса, а каждому значению радиуса окружности –
значение ее длины и т.д. Но в реальной жизни все намного сложнее. Как зависит
теплопроводность некого металла, о которой мы упоминали выше, от температуры? С
одной стороны – это четкая функциональная зависимость, протабулированная
во многих справочниках[5] по
свойствам веществ. Но с другой стороны, на это физическое свойство металла
могут влиять и некие неучтенные факторы – незначительные примеси, форма образца
при замере теплопроводности, возраст («усталость») металла и т.д. и т.п. На
сайте http://twt.mpei.ac.ru/MCS/Worksheets/Thermal/T-T-2-Tab-3-04.xmcd можно
провести аппроксимацию табличных данных по теплопроводности разных металлов с
помощью полинома переменной степени и вычислить искомое значение. Плотность
раствора соли также может неоднозначно зависеть от температуры и концентрации:
соль может иметь примеси, вода, в которой ее растворили, может быть тоже не
совсем чистой и т.д. На сайте http://twt.mpei.ac.ru/TTHB/1/Water-chem/C-NaCl.html
расположены онлайн расчеты плотности водного раствора этой соли в зависимости
от температуры и концентрации. Тут уже статистическая обработка ведется не на
плоскости, а в объеме: у соответствующей функции не один, а два аргумента.
Технологии получения подобных зависимостей по табличным и прочим данным
посвящена первая глава «Свойства рабочих тел и теплоносителей для
теплотехнических расчетов» книги [2].
Видя в книге или
Интернете таблицу с парами значений, не так просто определить, что это –
функция или корреляция, и что применить к этим данным – интерполяцию
(проведение линии строго через точки – рис. 1) или аппроксимацию (сглаживание,
проведение линии вблизи точек – рис. 5 и 10).
Мы уже упоминали
линейную интерполяцию – см. рис. 2. В среде Mathcad есть встроенная функция linterp(X, Y, х), которая формирует функцию
пользователя с аргументом х для интерполяции отрезками прямой
линии точек с координатами, хранящимися в векторах X и Y. При
такой кусочно-линейной интерполяции
необходимо, чтобы исходные векторы данных были одного размера, хранили
вещественные числа, а в векторе X элементы располагались в порядке возрастания. На
авторском сайте http://communities.ptc.com/videos/1512 показана анимация работы
функции linterp – поведение прямой линии через
пару очередных точек при линейной интерполяции данных.
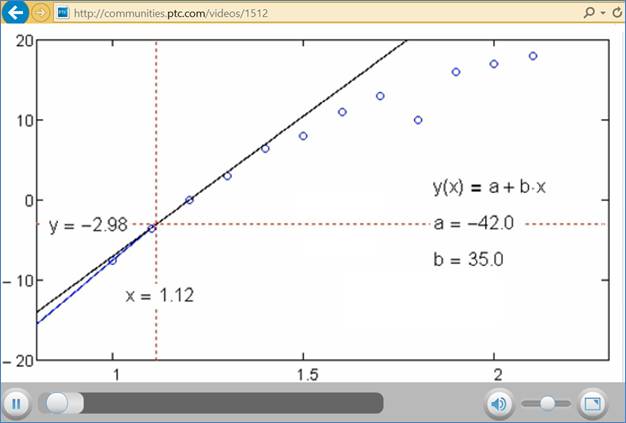
Рис. 12.Кадр анимации линейной
интерполяции
Линейная интерполяция
очень проста в реализации. Но «иная простота хуже воровства»: при такой
упрощенной интерполяции функция получается угловатой, а природа, повторяем, не
терпит острых углов и старается их сгладить. Вспомним, как морские волны
превращают острые обломки камней в гладкую гальку. Кроме того, ломаная функция,
состоящая из отрезков прямой линии, имеет в качестве первой производной набор
констант. Вторая же производная такой функции вообще равна нулю (украдена!) во
всех точках, кроме «угловых», в которых вторая производная просто не
существует. Это часто затрудняет применение к такой функции некоторых численных
методов, например, поиск нуля или минимума – см. пример на рис. 8, где была
задействована «угловатая» функция.
Если через две точки
можно провести прямую линию (см. рис. 2 и 12), то через четыре точки –
кубическую параболу. На этом основана кубическая сплайн-интерполяция табличных
зависимостей. Она более сложна в реализации, чем линейная интерполяция, но
лишена «угловатых» недостатков, отмеченных выше. На сайте http://communities.ptc.com/videos/1418 показана авторская анимация
интерполяции кубическими сплайнами. Один кадр этой анимации отображен на рис.
13.
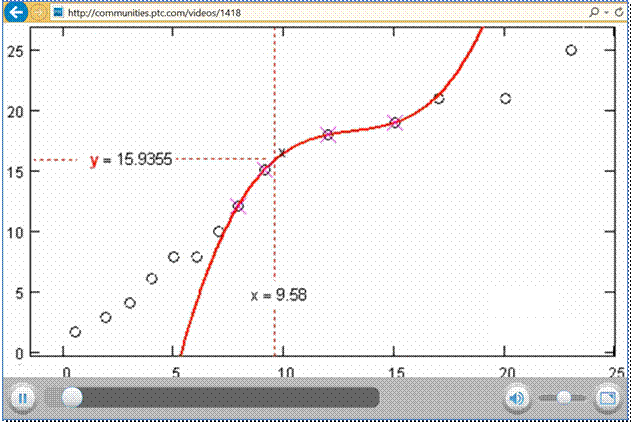
Рис. 13. Анимация
сплайн-интерполяции
В среде Mathcad сплайн-интерполяцию можно
реализовать с помощью функций lspline, psplineи cspline. Префиксы l, p и
с отмечают, по какой зависимости будет вестись экстраполяция (нахождение значений
воссозданной функции вне интервала дискретных значений вектора X). А
именно: l
(эль) – линейно
с опорой на две крайние точки, р
(пи) – по параболе с опорой на три крайние точки и с (си) – по кубической зависимости с опорой на четыре крайние
точки.
Сплайн-интерполяция
широко применяется в компьютерной графике, когда, например, необходимо через
фиксированные точки какого-либо объекта провести гладкую линию или поверхность.
Есть такая технология создания компьютерных мультфильмов. На человеке крепят
светящиеся точки, человек двигается, а три координаты этих точек фиксируются
компьютером. Затем компьютер проводит через эти точки криволинейную гладкую
поверхность или кусочки поверхности и воссоздает (оживляет, анимирует) движение
виртуального человека.
Экстраполяцию
по заданным точкам в среде Mathcad
можно реализовать и с помощью встроенной функции Predict
(предсказание), в которую заложен более сложный алгоритм. На рисунке 14
показано как эта функция предсказывает значения функции пользователя y(x):
на первых десяти точках значения заданной функции довольно хорошо
предсказываются, а потом происходит срыв…
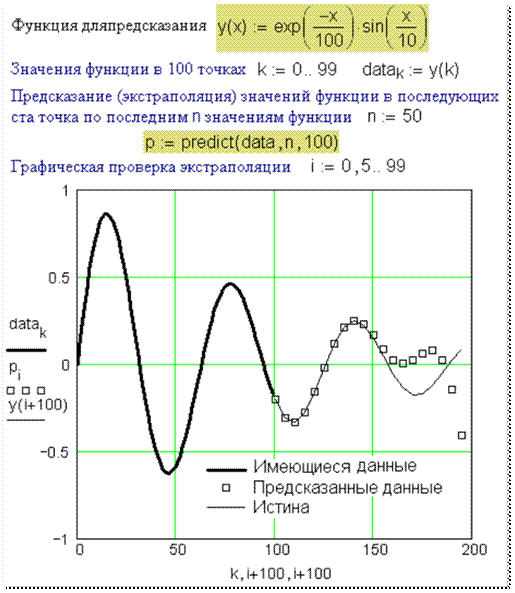
Рис. 14. Предсказание в среде Mathcad
Пусть читатель
попробует с помощью сайта, показанного на рис. 14, предсказать температуру
воздуха или курс доллара на ближайшую неделю, опираясь на данные прошедшей
недели, месяца, года и т.д. Затем по прошествии этой «будущей недели» сравнит
прогноз с реальными наступившим событиями.
В среде Mathcad есть много функций, позволяющих
обрабатывать дискретные случайные или закономерные данные – сглаживать их
(аппроксимировать), строить по ним интерполяцию или экстраполяцию. На рисунке
15 показан сайт Интернета, созданный с помощью пакета Mathcad, на котором проводится
аппроксимация табличных данных с помощью произвольной функции трех аргументов.
На рисунке показана работа с так называемой логистической[6]
функцией. С ее помощью можно описать три основные фазы изменения многих
объектов и явлений живой и неживой природы: возникновение, бурное развитие и
умирание (затухание). Конкретный пример: количество паровозов в мире сначала
росло медленно, затем наблюдался бурный рост их производства, а потом их
постепенно вытеснили тепловозы и электровозы…
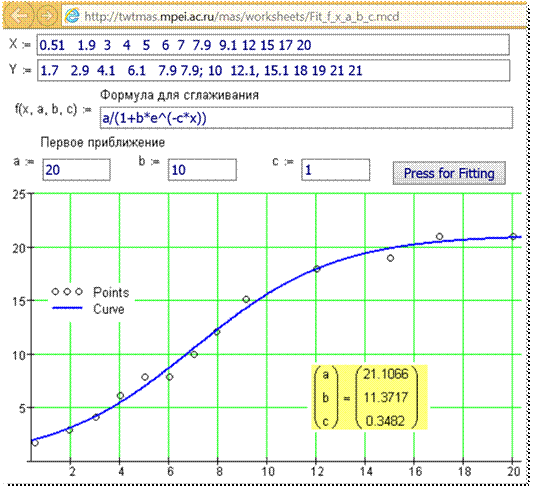
Рис. 15. Сглаживание табличной
зависимости по произвольной формуле
В текстовое окно с
меткой f(x, a, b, c),
показанное на рисунке 15, можно вставлять аппроксимирующие функции другого
вида. В сам же пакет Mathcad
встроены следующие функции с постфиксом fit (fitting), предназначенные для такой
работы:
expfit(vx,
vy,
[vg][7])–аппроксимация по формуле a ∙ eb
∙ x + c
lgsfit(vx, vy, vg) –
1 + b∙ e-c ∙ x
lnfit(vx, vy) – a ∙ ln(x)
+ b
logfit(vx, vy, vg) – a ∙ ln(x + b) + c
medfit(vx,
vy) – a + b ∙ x (альтернативный алгоритм,
реализующий не минимизацию суммы квадратов отклонений (см. рис. 6), а медиан-медианную линейную регрессию для
расчета коэффициентов а и b
(см. рис. 16)
pwrfit(vx, vy, vg) – a ∙ xb
+ c
sinfit(vx, vy, vg) – a ∙ sin(x + b) + c
linfit(vx,
vy,
F) – линейная (lin)
комбинация элементарных функций
genfit(vx,
vy,
vg, F)
– регрессионный анализ в общем (gen–general) виде
Из этого списка «фитинговых» функций несколько выпадает функция medfit,
в имени которой сокращение med
означает не вид аппроксимирующей
функции, как у других функций в списке, а метод
линейной аппроксимации. Функция medfit как и функция line (см. рис. 9) предназначена для
решения задачи линейной регрессии. Но в функцию medfit заложен не метод наименьших
квадратов, а метод медиан-медианной регрессии с
минимизацией суммы абсолютных значений медиан
ошибок в узлах[8].
На рисунке 16 показано сравнение регрессионного анализа параметров наших
студентов, проведенного методом наименьших квадратов и медиан-медианным
методом.
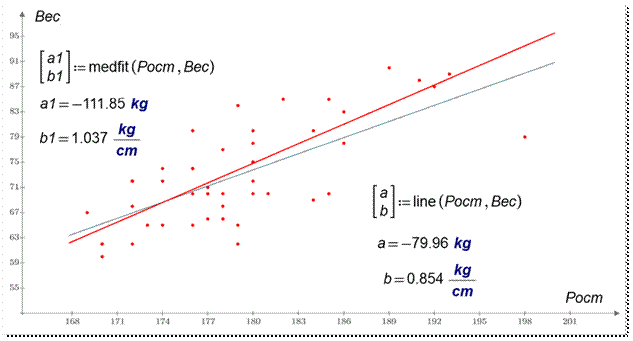
Рис. 16. Сравнение результатов
обработки данных медиан-медианной регрессией (medfit)
и методом наименьших квадратов (line)
Какая прямая на рис.
16 ближе к истине? Или спросим несколько иначе – в какой прямой меньше лжи (см.
второе название статьи)? Ответ на этот вопрос[9], если,
конечно, он вообще существует, зависит, в частности, от того, какое распределение заложено в анализируемые
случайные величины. В среде Mathcad,
кстати говоря, есть набор встроенных функций для генерации случайных величин по
разным законам распределения.
Но нередки случаи,
когда не наблюдается корреляции данных, например, так, как это выявлено при
исследовании статистической зависимости между баллами ЕГЭ по математике и
результатами контрольной работы [3]. Диаграмма рассеяния (рис. 17) ясно дает
понять, что остаточный уровень школьных математических знаний слабо зависит от
полученных на ЕГЭ баллов, причем дальнейший регрессионный анализ данных не
имеет смысла.

Рис.
17. Диаграмма рассеяния между баллами за контрольную работу и баллами ЕГЭ по
математике
С другой стороны,
предварительный анализ данных может помочь выявить и слабые корреляции. Так, например,
была обнаружена, хотя и незначительная, но отрицательная корреляционная связь
между временем, проводимым студентами за компьютером в целях развлечений, и
успешностью сдачи ЕГЭ по математике [4]. Для студентов из небольших городов она
равна –0.04, а для студентов из крупных городов она равна –0.25.
Мы видим, что
приступая к статистической обработке случайных величин желательно
предварительно построить графики и диаграммы для визуального анализа данных.
Так, встроенная в Mathcad
функция histogram позволяет построить частотную характеристику (гистограмму) выборки. На рисунке 18
графически показана частота появления того или иного значения роста у нашей
полусотни студентов с точностью в один сантиметр.
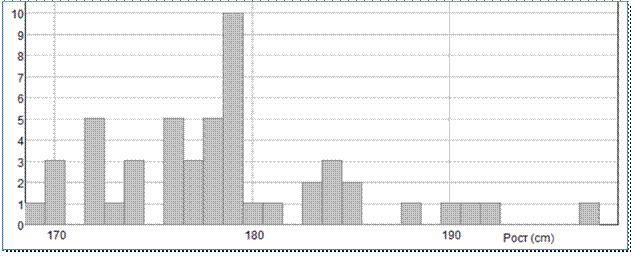
Рис.18. Пример гистограммы в
среде Mathcad
Так из гистограммы на
рис. 16 видно, что больше всего студентов (10 человек) имеют рост 179 см. Но какую-то статистическую закономерность на
рис. 16 увидеть довольно сложно. Если бы наша выборка студентов была бы намного
больше (студенты всего вуза или всей страны), то мы бы увидели, что на
гистограмме четко прорисовалась бы некая колоколообразная кривая – кривая нормального распределения: очень мало
людей имеют очень низкий или очень высокий рост, а большое количество людей
имеют некий средний (среднестатистический) рост.
Из рисунка 18 видно,
что наша гистограмма немного сдвинута относительно нормального распределения.
Но вспомним еще раз второе название нашей статьи: «Есть ложь, наглая ложь и…
статистика». В этом изречении скрыт и такой нюанс. Люди при опросах часто
вольно или невольно слегка искажают информацию о себе. Можно предположить, что
некоторые студенты, называя вслух свой рост, прибавляли к нему 1, 2 или даже 3
см. Скажем несколько мягче. Низкие студенты округляли свой рост до сантиметра в
большую сторону (было, например, 156.3 cm – стало 157 cm), а высокие проводили округление
более правильно (было, например, 179.3 cm – стало 179 cm). В таких опросах (при переписи
населения, например) часто лукавят женщины: убавляют себе возраст и/или вес,
приписывают себе несуществующего мужа и т.д.
В интернете можно
найти не очень качественную, но очень интересную фотографию «живой» гистограммы
роста людей – рис. 19.
Рис. 19. Живая гистограмма роста
человека
Группа игроков
выстроилась на футбольном поле по росту, но не в одну шеренгу, а в колонну с
разным числом людей в каждом ряду. Каждый ряд соответствовал определенному
росту: 4 фута и 9 дюймов (144.78 cm – этот самый левый ряд на рис. 19
пуст), пять футов (152.4 cm)
и так далее до 6 футов и 5 дюймов (195.58 см). В таком «опросе» схитрить при
ответе о собственном росте будет довольно сложно: завышение этого параметра на
2 – 3 см будет сразу заметно в соответствующем ряду, если только не встать на
цыпочки. В диаграмме, показанной на рис.18, в середине нет пустых рядов, какие
мы наблюдали на рис. 18, потому, что шаги на этих гистограммах разные – один
сантиметр и один дюйм (2.52 cm).
Если в США и Англии
рост человека измеряют в футах и дюймах[10], то в
старой России для этого брали аршины и вершки[11], но
аршины (конкретно два аршина) по
умолчанию не указывали. Дело в том, что рост взрослого человека очень редко был
меньше двух аршин (примерно 142 см) или больше сажени (трех аршин – примерно
213 см). Рост лошади в холке также измеряли в вершках без указания на
дополнительные два аршина. Читаем у Тургенева в повести «Муму»: «Из числа всей
ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати
вершков роста, сложенный богатырем и глухонемой от рожденья». Несложно
подсчитать «богатырский» рост Герасима – примерно 196 см. На рисунке 20
построена гистограмма роста наших студентов (см. рис. 5) с шагом в один вершок.
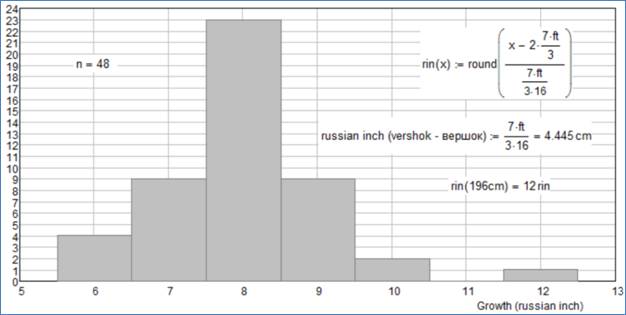
Рис. 20. «Вершковая» гистограмма
роста студентов.
На
«вершковой» гистограмме на рис. 20 уже четко просматривается некий
«статистический колокол» – кривая нормального распределения. Студенты по росту
разбиваются на 5 условных групп: низкого роста (4 человека с шестивершковым
ростом), скорее низкого, чем высокого роста (9 человек – 7 вершков), среднего
роста (23 человека – 8 вершков), скорее высокого, чем низкого роста (9 человек,
9 вершков) и высокого роста (2 человека, 10 вершков). Один студент выпал из
нашей «статистики» – оказался «герасимовского» роста
в 12 вершков: исключение только подтверждает правило. Сравнивая рисунки 18 и
20, можно сказать словами персонажа одного мультфильма: А в вершках-то наша
гистограмма красивее и намного «статистичнее»!
Кстати, здесь мы невольно затронули важнейший для обработки данных вопрос об
установлении оптимального шага при обработке выборки. Ведь можно было бы
группировать данные каким-то иным способом. Например, по признаку попадания
значения роста на интервалы длиной в 1 метр, начиная с нуля (тогда гистограмма
имела бы вид прямоугольника).
На связь роста и веса
человека влияет много факторов. Т.е. это корреляция, а не функция. Один из
важных факторов – это возраст человека. Немногим людям удается сохранить свой
вес таким, каким он был «хорошим» в молодости[12]. На
веса человека также большое влияние оказывает его генетика (наследственность)
и, конечно, образ жизни. У человека, как и у автомобиля (см. ниже) возраст
определить несложно. А вот «пробег» человека, конкретно говоря, число шагов,
которые он сделал за свою жизнь, тоже хорошо было бы измерять для более точного
определения взаимозависимости веса и роста. Пробег замеряет спидометр
автомобиля. Некоторые люди на прогулках или пробежках используют шагомер.
Итак, автомобиль с
его возрастом и пробегом!
Если читатель
перейдет по ссылке, отмеченный в списке литературы [1], то он может узнать, как
в среде Mathcad
проводился более сложный регрессионный анализ – как определялась формула, по
которой можно оценить стоимость подержанного автомобиля в зависимости от его
возраста и пробега – см. таблицу (скачать Mathcad 15 файл с этими данными >>>).
Таблица.
Данные о
стоимости подержанного автомобиля определенной марки.
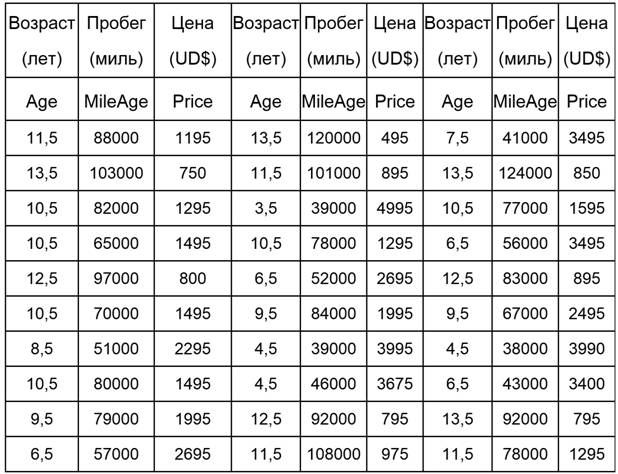
Первому автору статьи
тут вспоминается одна история, свидетелем которой он был в Западной Германии в
80-х годах прошлого века. Один немецкий профессор (автор был на стажировке в
одном немецком университете) решил быстро продать свой автомобиль за 2000 марок
и выставил его по этой низкой цене на местном автомобильном «блошином» рынке. К
нему довольно долго подходили потенциальные покупатели, осматривали машину,
задавали вопросы, но все эти контакты оказывались безрезультатными. Но тут
подходит один довольно бойкий молодой человек, покупает, как говорится, не
глядя машину, меняет на ней… ценник и тут же на глазах изумленного профессора
перепродает ее за 4000 марок... Этот перекупщик умел сходу правильно оценить
стоимость подержанного автомобиля и понимал, что заниженная цена также плоха
для торга, как и завышенная. Проецируя этот тезис на наших студентов, можно
сказать, что слишком низкий рост также плох для жизни, как и слишком высокий…
На рисунках 21, 22,
23 и 24 можно видеть графики, построенные по точкам из «автомобильной» таблицы.
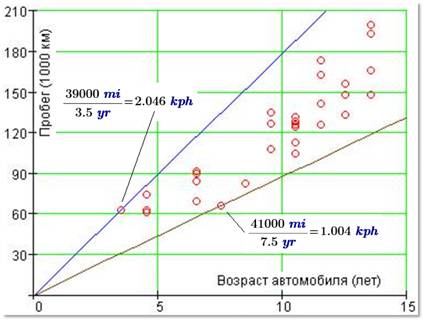
Рис. 21. Корреляция пробега автомобиля
и его возраста
Из
рисунка 21 видно, что область корреляции пробега автомобиля от его возраста (некий
эксплуатационный клин) – это область, ограниченная двумя условными лучами:
минимальная и максимальная средние скорости автомобилей. В нашей выборке они
такие: 1.004 км/ч (7.5 лет и 41 000 миль пробега) и 2.046 км/ч (3.5 года и 39
000 миль пробега). Отсюда вывод – если вам предлагают купить подержанный
автомобиль, параметры которого не попадают в наш «клин» (1-2 км/ч), то это
значит, что машину либо слишком интенсивно эксплуатировали (скорость больше 2
км/ч), либо она непонятно почему простаивала (скорость меньше 1 км/час), либо у
нее… подкручен спидометр. Возраст машины скрыть намного трудней.
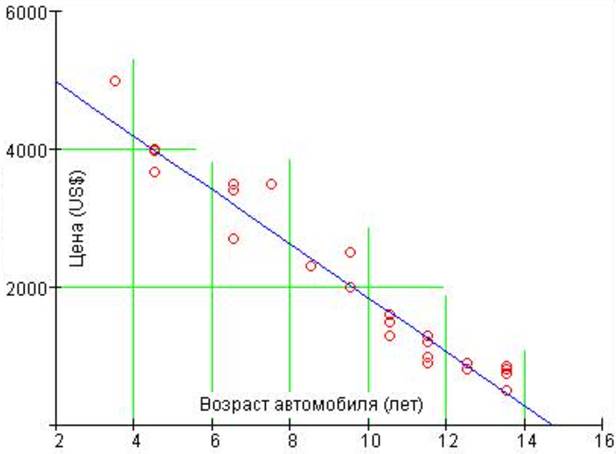
Рис. 22. Корреляция цены
автомобиля и его возраста
Цена
автомобиля от возраста зависит линейно (a + b x – рис. 2 и 22). Никакой другой
более сложной зависимости из точек, разбросанных на графике рис. 22, выудить
невозможно. В нашем случае после каждого года пробега с цены машины нужно будет
скидывать в среднем по 393 доллара.
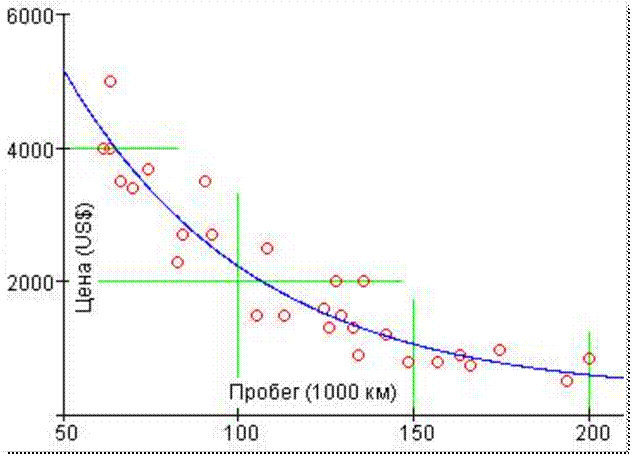
Рис. 23. Корреляция цены
автомобиля и его пробега
Зависимость
цены автомобиля от пробега (рис. 23) более сложная – она меняется
экспоненциально: (a + eb x). При такой зависимости (b < 0) цена машины никогда не упадет
до нуля, чего не скажешь о зависимости цены от возраста (рис. 22), когда в
районе 14-15 лет автомобиль становиться «бесценен» в двух смыслах: либо у него теперь
нулевая цена (наш смысл) либо автомобиль стал… «бесценным» музейным экспонатом.
Статистическая
обработка данных по цене подержанного автомобиля позволила создать Mathcad-сайт для оценки данной
корреляции – см. рис. 24.
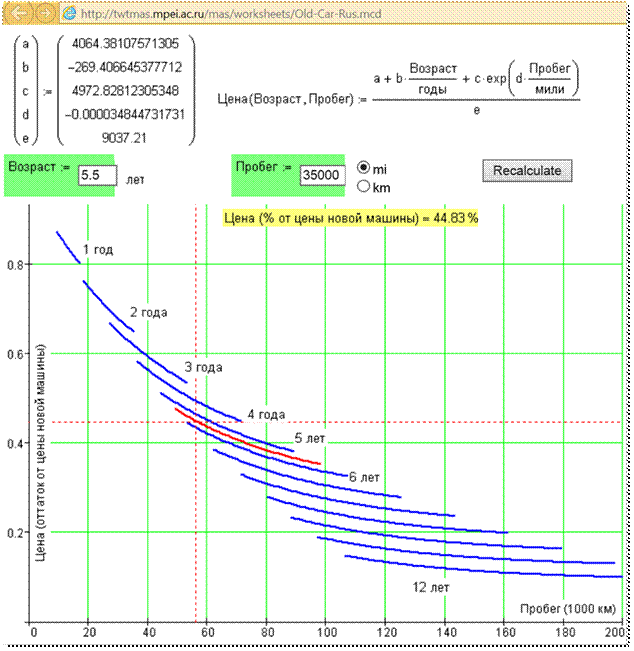
Рис. 24. Сайт по оценке стоимости
подержанного автомобиля
По графику на рис. 24
можно не только получить оценочную стоимость старого автомобиля, но и отсечь
заведомо сомнительные варианты, зафиксированные на рис. 21 (параметры вне
скоростного клина), когда пробег автомобиля не соответствует его возрасту. Mathcad-документ,
по которому велись расчеты, можно «скачать» по адресу: ftp://twt.mpei.ac.ru/ochkov/Auto.
Первый автор статьи
два раза приобретал автомобиль по схеме treid-in, когда в стоимость новой машины
входила стоимость старой, сдаваемой на комиссию. Так вот, оба раза цена старого
автомобиля, предлагаемая салоном, отличалась от той, которая была рассчитана с
помощью сайта, показанного на рис. 24, не более, чем на 5%.
А можно ли оценить в
рублях не автомобиль, а человека по его возрасту и… пробегу, если под пробегом
иметь ввиду не число пройденный шагов, а его деловые качества, которые
приобретаются в результате «пробега»: учебы, работы по специальности, повышения
квалификации, самообразования, решения разных жизненных и производственных
(офисных) коллизий…?
Кому-то этот вопрос
покажется несколько кощунственным – как можно человека измерять рублями,
долларами, фунтами? Но тут можно упомянуть футболистов, многие из которых
бегают по полю с «ценниками», где указаны суммы, какие нужно уплатить при
переводе футболиста в другой клуб. У других специалистов высшей квалификации
цена не прописана так явно, но она негласно фигурирует в досье и при
переговорах по переходу, например, менеджера из одной фирмы в другую.
Если же под
стоимостью человека подразумевать его капитал, то тут можно наблюдать разные
кривые в координатах «стоимость – возраст» (см. рис. 22).
Одни люди начинают с
нуля, а потом создают себе капитал. Другие же растрачивают средства, полученные
по наследству, «скатываясь по наклону», показанному на рис. 22. Оптимальным же
или самым «красивым» считается вариант, когда человек получает какой-то
стартовый капитал и приумножает его, оставляя затем наследникам какую-то
разумную сумму и потратив львиную долю на благотворительность, основав,
например, университет или поддержав свою Alma Mater, или свой родной город.
Но если говорить о
цене человека, имея в виду не его капитал, а его ценность как специалиста, то
тут тоже можно видеть некую горбатую кривую зависимости этого основного
параметра человека от его возраста. Пик (максимум) на этой кривой может
приходиться на разный возраст у разных специалистов-профессионалов. У
упоминавшихся футболистов это 25 – 30 лет, у руководителя компании 40 – 60 и
т.д.
Но вернемся к гистограммам, показанным на рис. 17-19.
Давайте проведем глобальный
(мысленный) статистический эксперимент и у всех взрослых людей на планете
измерим какой-либо параметр: вес, рост (см. выше), ум и т.д. – словом все то, что можно измерить числом или
оценить лингвистическими критериями (гений, талант, очень умный, просто
умный... совсем дурак, если говорить об умственных способностях человека).
Полученные точки превратим в
кривые, где по оси X отложим
параметр человека, а по оси Y –
процент людей с данным параметром. При этом статистическую обработку проведем
отдельно для мужчин и женщин. Что мы получим?
Статистический случай 1:
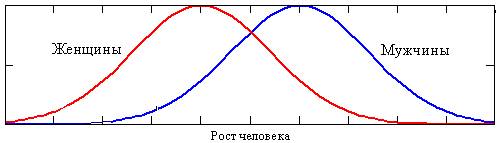
Рис. 25. Гистограмма роста мужчин и женщин
Кривые случая 1 (рис. 25) получаются для тех параметров человека, значение
которых у мужчин больше, чем у женщин (рост, вес, сила мышц и т.д.). Это, как
многие считают, связано с эволюцией – если среднестатистическая мужская особь
крупнее женской, то новые поколения укрупняются. У пауков, например, самцы
намного меньше самок и пауки сейчас, слава богу, более мелкие, чем в
доисторические времена.
Статистический
случай 2:
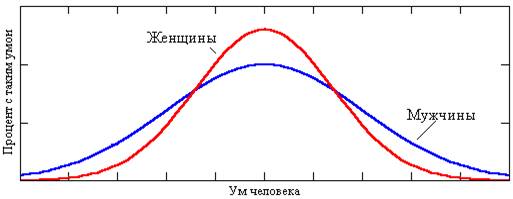
Рис. 26. Гистограмма интеллектуальных качеств мужчин и
женщин
А так (случай 2: рис. 26) могут выглядеть кривые для параметров, значения
которых у человека за последние несколько тысяч лет не менялись – ум, например.
Многие вполне обоснованно полагают, что современный человек, если убрать налет
образованности и культуры, не намного умней древнего грека
или египтянина. Среди мужчин гениев (нобелевских и прочих лауреатов, великих
изобретателей, знаменитых писателей и художников – см. правый край графиков на
рис. 26) больше лишь потому, что и… дураков среди мужчин достаточно (левый край
графика). Но средняя женщина умнее
среднего мужчины – центр «женской» кривой приподнят за счет меньшего разброса
по краям: площади фигур под графиками одинаковы – никого не обижая, будем
считать, что Господь Бог или Природа (кто как для себя считает) одинаково
наделили умом обе половины человечества.
С этим можно, конечно,
поспорить, но… еще раз взглянем на второе название статьи.
Выводы
Пакет Mathcad (как, впрочем, и другие пакеты)
имеет богатый набор встроенных средств для статистической и прочей обработки
массивов данных. Их освоение поможет решать учебные и производственные задачи
и, в частности, отличать ложь (неверные или несколько искаженные исходные
данные) от… статистики.
Литература:
1.
Очков
В.Ф. Цена подержанного автомобиля или Путь от корреляции к регрессии в среде
Mathcad // КомпьютерПресс. № 9. 2001 (http://twt.mpei.ac.ru/ochkov/car/car.htm)
2.
Теплотехнические
этюды с Excel, Mathcad и Интернет / Под общ. ред.
В.Ф. Очкова. Издательство БХВ-Петербург. 2014. – 336 с. ISBN 978-5-97753352-2 (http://twt.mpei.ac.ru/ochkov/TTMI).
3.
Богомолова
Е.П., Максимова О.В. Проблемы оценивания результатов ЕГЭ по математике. // Alma Mater Вестник высшей школы №
9, 2014, с. 56–60.
4.
Богомолова
Е.П., Максимова О.В. Влияние компьютерной поддержки математики на успеваемость
студентов технических вузов // Открытое образование № 6, 2014, с. 65-71.