УДК 621.039.54
Теплотехнические расчеты в
среде Mathcad
Очков В.Ф.[1],
кандидат техн. наук, Утенков В.Ф., кандидат техн. наук, Орлов К.А., бакалавр
техн. наук.
МЭИ
В настоящее время для решения учебных, инженерно-технических и научных задач наряду с традиционными языками программирования (fortran, Pascal, BASIC, C и др.) и табличными процессорами (Excel) широко используются специализированные математические пакеты (Maple, Mathematica, MatLab, Mathcad и др.), которые позволяют специалистам в конкретной научно-технической области быстро осваивать работу на компьютере и реализовать на них математические модели, не вдаваясь в тонкости программирования и не прибегая к услугам программистов [1].
Цель статьи ¾ познакомить читателей журнала с методикой решения некоторых типовых теплотехнических задач в среде Mathcad. Mathcad — это зарегистрированная торговая марка фирмы MathSoft, Inc. (www.mathsoft.com): сокращение английской фразы: Mathematical Computer Aided Design — математическое проектирование с помощью компьютера.
Ниже приведены примеры решения типовых теплотехнических задач, которые иллюстрируют особенности и преимущества работы в среде Mathcad. Задачи предельно упрощены ¾ акцент делается не на сути задач, а на показе методики их решения в среде Mathcad.
Пример 1. Расчет термодинамических свойств воды и
водяного пара
На рис. 1 показано формирование в
среде Mathcad двух функций пользователя:
vw(P),
возвращающей удельный объем кипящей воды
на линии насыщения (vw) в зависимости от
давления P (рис. 1), и функции hss(T, P), возвращающей
удельную энтальпию перегретого пара (hss) и в зависимости от температуры T и давления P.
Расчет удельного объема кипящей воды на линии насыщения построен на интерполяции (здесь задействована встроенная Mathcad-функция interp) кубическим сплайном (cspline) табличных данных [2], хранящихся в двух векторах-строках: P — табличные значения давления, выраженные в МПа, и V — табличные значения удельного объема, выраженные в л/кг (дм3/кг).
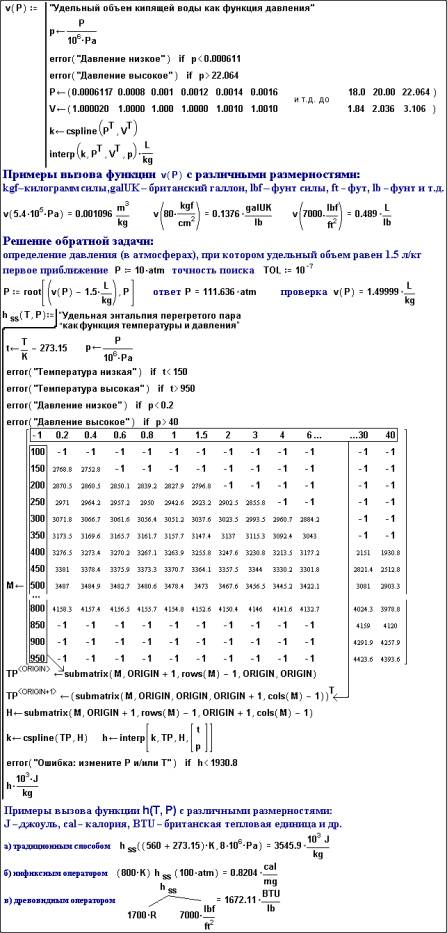
Рис. 1. Формирование в среде Mathcad функций пользователя, возвращающих удельный объем кипящей воды на линии насыщения и удельную энтальпию перегретого пара
Интерполяция сплайном для определения
удельного объема кипящей воды ведется в диапазоне давления от 611.7 Па до 22.064
МПа (критическое состояние). Функция error отслеживает значение аргумента P, прерывает выполнение вычислительной
процедуры и выдает пользовательское сообщение об ошибке (“Давление
низкое” или “Давление
высокое”), если значение аргумента не попадает в оговоренный диапазон (эту
работу выполняет оператор if). Механизм вывода
сообщений об ошибках в среде Mathcad (встроенных и пользовательских) таков. При
возникновении ошибки цвет функции на экране дисплея меняется на красный. Если
после этого к функции подвести курсор мыши, то «выпадает» сообщение об ошибке ¾
встроенное или пользовательское.
Созданную функцию vw(P) можно использовать в расчетах с различными размерностями давления, объема и массы: на рис. 1 используются встроенные размерности в английском написании: Pa ¾ паскаль, atm ¾ атмосфера физическая, kgf — килограмм силы, galUK — британский галлон, lb — фунт и lbf — фунт силы и ft — фут; российские названия размерностей в расчетах возможны через механизм пользовательских размерностей ¾ см. рис. 2. Пересчет размерностей системой Mathcad ведется автоматически, что является одним из преимуществ этого пакета по сравнению с традиционными языками программирования. При этом отслеживается правильность действий с размерностями: калории с джоулями сложить можно, а метры с килограммами ¾ нельзя.
В табл.1 приведен список имен единиц измерения физических величин, встроенных в Mathcad
Табл. 1
|
Физическая величина |
Единица |
|
активность (activity) |
Bq |
|
время (time) |
day (день), hr (час), min,
s, sec и yr (год) |
|
вязкость динамическая (dynamic viscosity) |
poise |
|
вязкость кинематическая (cinematic viscosity) |
stokes |
|
давление (pressure) |
atm (атмосфера физическая), in_Hg (дюймы ртутного столба), Pa, psi (фунт силы на квадратный дюйм) и torr (мм ртутного столба) |
|
длина (length) |
cm, ft (фут),
in (дюйм), km, m, mi (миля),
mm и yd (ярд) |
|
доза (dose) |
Gy и Sv |
|
емкость (capacitance) |
F, farad, mF, nF,
pF и statfarad |
|
заряд (charge) |
С, coul и statcoul |
|
индуктивность (inductance) |
H, henry, mH, mH и stathenry |
|
индукция магнитного поля (magnetic flux density) |
gauss,
stattesla, T и tesla |
|
количество вещества (substance) |
mole (моль) |
|
магнитный поток (magnetic flux) |
statweber, Wb
и weber |
|
масса (mass) |
gm, kg, lb (фунт), mg, oz, slug, ton и tonne |
|
мощность (power) |
hp, kW, W, и watt |
|
напряженность магнитного поля (magnetic field strange) |
Oe и oersted |
|
объем (volume) |
fl_oz, gal,
galUK, L, liter и mL |
|
освещенность (illuminosity) |
lx |
|
площадь (area) |
acre и hectare |
|
потенциал (potential) |
kV, KV, mV,
statvolt, V и volt |
|
проводимость (conductance) |
mho, S, siemens
и statsiemens |
|
сила (force) |
dyne, kgf,
lbf, N и newton |
|
сила света (luminosity) |
cd и Im |
|
скорость (velocity) |
c, kph и mph |
|
сопротивление (resistance) |
kW, MW, ohm,
statohm и W |
|
температура (temperature) |
K и R |
|
ток (current) |
A, amp, KA, mA, mA и statamp |
|
угол (angular) |
deg, rad и str |
|
ускорение (acceleration) |
g (ускорение свободного падения) |
|
частота (frequency) |
GHz, Hz, kHz, KHz и
MHz |
|
энергия (energy) |
BTU, cal, erg, J, joule и
kcal |
Для работы с физическими величинами в среде Mathcad предусмотрено диалоговое
окно «Ввод размерности» («Insert Unit»),
определяющее физическую величину (Dimension ¾ Length ¾ длина), единицу (Unit ¾ Kilometers
(km) ¾ километры) и систему единиц
(System ¾ SI ¾ международная система; в
среде Mathcad кроме нее встроены системы «метр-килограмм-секунда»,
«сантиметр-грамм-секунда» и британская; по умолчанию европейская версия Mathcad
оперирует международной системой единиц).
Возможность работы с размерностями физических
величин позволяет называть Mathcad не просто математическим, а физико-математическим
пакетом. Часто, решая физическую задачу, пользователь делает ошибки не в
формулах и не в счете, а в размерностях
физических величин. Пакет Mathcad
поддерживает основные системы единиц и, что очень важно, ведет контроль за соответствием размерностей.
После вывода значения переменной система
Mathcad к константе «припечатывает» основную единицу выбранной системы (SI,
например): P:= 20 atm P = 2.026 106
Pa.
После этого пользователь волен заменить размерность (здесь паскали ¾ единицы давления) на любую
другую.
На рис. 1 показано также решение через встроенную Mathcad-функцию root (поиск корня уравнения) обратной задачи — определение давления при заданном значении удельного объема кипящей воды.
Расчет удельной энтальпии перегретого пара (рис. 1) ведется также кубическим сплайном, но уже через двумерную интерполяцию. Табличные значения энтропии (кДж/кг) заносятся в матрицу М, где соответствующие значения температуры (градусы Цельсия) и давления (МПа) формируют боковик и шапку таблицы, что позволяет не только легко корректировать данные, но и просто использовать их как справочную таблицу. К встроенным сообщениям об ошибках неверных значений аргументов (температура и/или давление пара не попали в оговоренный диапазон) добавлено новое — “Ошибка: измените P и/или T”. Она возникает в том случае, при сплайн-интерполяции будут «захвачены» элементы массива M, где отсутствуют табличные данные, и рассчитанное значение энтальпии окажется меньше наименьшего табличного значения (1930.8 кДж/кг).
Пользовательскую функцию hss(T, P) с двумя аргументами можно вызывать в традиционной форме (функция), а также инфиксным и древовидным оператором (см. рис. 1).
Аналогичным образом можно построить и другие функции термодинамических свойств воды и водяного пара — удельная энтальпия кипящей воды на линии насыщения hw, удельная энтальпия сухого пара на линии насыщения hs, удельная энтропия кипящей воды на линии насыщения sw, удельная энтропия сухого пара на линии насыщения ss и удельная энтропия перегретого пара sss. Соответствующий Mathcad-документ имеет имя wat&stea.mcd (water and steam) и хранится на ftp-cервере по адресу: ftp://twt.mpei.ac.ru/ochkov/thermo.mcd. Этот файл можно по сети Internet скопировать на компьютер конкретного пользователя и задействовать его в термодинамических расчетах, что и будет сделано в примере 2.
Подход к составлению функций пользователя, возвращающих термодинамические свойства воды и водяного пара в зависимости от параметров состояния, заложенный в Mathcad-документ на рис. 1, имеет свои достоинства и недостатки.
Преимущество в том, что созданные функции «автономны» и не зависят от остального содержимого рабочего документа (механизм локальных переменных). Пользователь может скопировать нужную ему функцию в свой файл Mathcad и использовать ее в процессе вычислений. Табличные значения всегда перед глазами пользователя и их легко исправить, дополнить.
Однако, если требуется несколько раз использовать функцию в процессе вычислений, то каждый раз придется при входе в функцию заново определять массивы с табличными данными. Второй недостаток – эти функции статичны, т.е. при попытке использовать новые, более точные табличные данные, придется редактировать большие массивы данных, что в среде Mathcad довольно проблематично: экран будет все время «убегать» не туда, куда нужно, мелькая перед глазами пользователя.
Для решения проблем, связанных с таким способом составления функций пользователя свойств воды и водяного пара, одним из авторов (К.А.Орловым ¾ e-mail oka@acsv.mpei.ac.ru) был предложен альтернативный способ организации вычислений, развивающий методику, описанную в [3]. В новом методе табличные данные хранятся в файлах на диске, а потом считываются в процессе открытия документа Mathcad. Это позволяет использовать их не только для вычислений в среде Mathcad, но также и в других пакетах. Редактирование данных не так удобно, но по-прежнему возможно. Однако при этом возникают свои сложности: при изменении табличных данных пользователю придется заботиться о соответствии размерности данных, хранящихся в файле, и размерности, которая «назначается» данным при их считывании в Mathcad (хранить в файле размерные величины невозможно). Вторая проблема – это необходимость указания явного пути нахождения файлов при считывании данных из них, так как при «внедрении» (Reference ¾ см. рис. 2) документа Mathcad в другой происходит изменение полного имени рабочего каталога и программа может не найти файлы с данными.
Новый метод позволяет, ко всему прочему, унифицировать процесс создания пользовательских функций, так как при интерполяции используются одни и те же табличные данные. Это позволило одному из авторов (К.А. Орлову) создать порядка 50 функций для свойств воды и водяного пара на линии насыщения, среди которых были и достаточно «экзотические» ¾ такие как функция зависимости удельной энтропии воды на линии насыщения от удельного объема пара на линии насыщения, при одинаковом давлении насыщения.
Судить о том, какой способ лучше, надо в каждом конкретном случае: при однократном вызове необходимой функции лучше использовать первый метод (см. пункт 3 на рис. 2), а при большом объеме расчетов можно использовать «мощь» второго метода (пункт 4 на рис. 2).
Некоторые особенности работы в среде Mathcad.
Интерфейс пользователя Mathcad довольно простой. Его основа операторы ввода и операторы вывода значений переменных и выражений.
В среде Mathcad три оператора ввода:
1.
A ¬
■ — ввод
значения локальной переменной, область видимости которой ограничена
местом ввода переменной и концом вычислительной процедуры, отмеченной
вертикальной чертой, фиксирующей начало и конец программного блока (программно
созданной функции пользователя ¾ см. рис. 1 и 3);
2.
A := ■ — ввод значения полуглобальной переменной, область
видимости которой — это часть Mathcad-документа, расположенная правее и ниже
места ввода переменной;
3.
A º ■ — ввод значения глобальной
переменной, область видимости — весь Mathcad-документ.
Кроме того, в Mathcad-документе возможны
ссылки на другой Mathcad-документ (на соответствующий Mathcad-файл на диске —
на файл с расширением mcd), переменные и пользовательские функции которого, становятся видимыми
в текущем Mathcad-документе. Этим приемом мы воспользуемся в следующем примере,
когда сделаем видимыми функции
термодинамических параметров воды и водяного пара при расчете
термодинамического цикла.
В среде Mathcad два оператора вывода:
·
A = — вывод численного
значения переменной или выражения;
·
A ® — вывод символьного
значения переменной или выражения (см. ниже пример 3).
Переменные в среде Mathcad могут хранить скалярные, векторные и матричные
величины.
Скаляром, а также элементом вектора и матрицы
может быть число (целое, вещественное или комплексное — см. элементы вектора V на рис.5), а также текст. С другой стороны,
элементом вектора или матрицы может быть новый вектор или матрица, что
позволяет строить довольно сложные структуры данных. В среде Mathcad
максимальное число элементов вектора или матрицы ¾ 8 миллионов.
Рассчитанные значения переменных могут быть
выведены в десятеричном (длина мантиссы ¾ 15 цифр), двоичном,
восьмеричном или шестнадцатеричном формате. При вводе числа в десятеричном
формате (обычный формат научно-технических расчетов) по умолчанию выводятся три
знака после запятой. Второе умолчание – если число больше 1000, то оно
выводится в научном формате: 1.387×103. Но пользователь может
нарушить это умолчание и изменить формат числа: 1386.7, например.
Имена переменных в среде Mathcad могут
содержать буквы латиницы, кириллицы и (чего нет в традиционных языках
программирования) греческого алфавита. Кроме того, в именах переменных
допустимы индексы. Все это позволяет давать переменным и функциям те имена,
которые закрепились за ними в процессе формирования той или иной научной
дисциплины и задолго до появления компьютеров.
Сравните запись одной и той же формулы на
языке BASIC и в документе Mathcad:
kappa = Pi() * SQR(mu)/A/B^C
c :=![]()
При публикации статей, текст которых
готовится на компьютере, формулы набираются, как правило, без проверки их
работоспособности при подстановке вместо имен переменных конкретных значений.
Формула «живет» как бы в двух формах: строка программы (см. выше пример на
языке BASIC) и формула в статье или книге, набранная с помощью какого-либо
текстового процессора ¾ с помощью, например,
утилиты Microsoft Equation, входящей в состав Word.
Среда Mathcad позволяет избежать такой раздвоенности, влекущей за собой
досадные опечатки. В формулы, введенные в среде Mathcad, которые, как мы уже
отмечали выше, почти не отличаются от формул, написанных от руки, можно не только
подставить контрольные значения. Допустимо по формулам построить графики и даже
создать анимацию.
Вторая «раздвоенность», мешающая полноценному
использованию компьютеров в научно-технических расчетах, заключается в
следующем. Как правило, между инженером (технологом,
исследователем) и компьютером стоит
программист, переводящий идеи
(вопросы) первого на язык ЭВМ. Использование программ типа Mathcad позволяет
исключить из этой цепочки посредника, который нередко искажает мысли
исследователя или просто не понимает его вопросов машине.
В пакет Mathcad интегрирован мощный
математический аппарат, позволяющий решать разнообразные задачи без
обращения к внешним библиотекам. Вот перечень групп встроенных функций Mathcad:
· функции
Бесселя (Bessel);
· функции
комплексных чисел (Complex Numbers);
· функции
решения дифференциальных уравнений и систем (задача Коши, краевая задача,
уравнения в частных производных — Differential Equation Solving);
· функции
типа выражения (Expression Type);
· функции
работы с файлами (File Access);
· функции
преобразований Фурье (Fourier Transform);
· гиперболические
функции (Hyperbolic);
· функции
интерполяции и экстраполяции (Interpolation and Prediction);
· логарифмические
и экспоненциальные функции (Log and Exponential);
· функции
теории чисел и комбинаторики (Numbers Theory/Combinatorics);
· функции
ступенек и условия (Piecewise Continuous);
· функции
плотности вероятности (Probably Density);
· функции
распределения вероятности (Probably Distribution);
· функции
случайных чисел (Random Numbers);
· функции
регрессии и сглаживания (Regression and Smoothing);
· функции
решения алгебраических уравнений и систем, а также оптимизации (Solving);
· функции
сортировки (Sorting);
· статистические
функции (Statistics);
· тригонометрические
функции (Trigonometric);
· функции округления и работы с частью числа (Truncation and Round-Off);
· функции
работы с векторами и матрицами (Vector and Matrix);
·
функции
волновых преобразований (Wavelet Transform).
Для ввода в расчет встроенных функции предусмотрено диалоговое окно
«Ввод функции» («Insert Function»), где пользователь может
отметить группу функций (Differential Equation Solving ¾ решение дифференциального
уравнения, например), просмотреть список функций, входящих в эту группу,
ознакомиться с сутью функции. В «подсказке» Mathcad дано более подробное
описание функции и даны типичные примеры их работы, которые могут быть
скопированы в рабочий документ и скорректированы для конкретной цели.
Если пользователя Mathcad встроенный математический аппарат не
удовлетворяет, то он может создать новые функции (на языке Mathcad или на языке
С) и использовать их в своих расчетах. Кроме того, пользователю доступны электронные книги Mathcad: численные
методы, термодинамика, решение дифференциальных уравнений, сопротивление
материалов, статистика, теория управления, финансы и многое другое. На сайтах Internet хранится
множество примеров, решения прикладных задач, которыми пользователи Mathcad
могут воспользоваться (см. конец статьи).
В среде Mathcad можно работать и с математическими операторами, которые вводятся через нажатие соответствующих кнопок панелей инструментов: взятие производных (первого и высших порядков), определенных и неопределенных интегралов, вычисление суммы, произведения, корней разной степени, пределов (включая справа и слева), работа с матрицами (транспонирование, вычисление детерминанта, векторное сложение и умножение и др.
Использование операторов в традиционном написании (суммы, корни, интегралы, дифференциалы и др.) повышает «читабельность» Mathcad-документов, максимально приближает их к листу бумаги с записями «от руки».
В среде Mathcad учитывается тот факт, что человек привык к делению математического аппарата на функции с аргументами и на операторы с операндами задолго до того, как он стал пользователем и в биографическом и историческом плане. Для компьютера нет разницы между функцией и оператором. И в том и в другом случае дело сводится к вызову некой вычислительной процедуры.
Пример 2. Расчет параметров цикла Ренкина
На рис. 2 представлен протокол расчета в
среде Mathcad термического кпд (коэффициента
полезного действия) цикла Ренкина.
В начале рис. 2 дана схема цикла Ренкина и
его T-S диаграмма: Mathcad-документы могут
иллюстрироваться не только текстами (комментариями), но и рисунками,
поясняющими суть задачи. Рисунки создаются в среде какого-либо графического
редактора (в среде, например, программы PaintBrush, входящей в состав Windows) и
переносятся в Mathcad-документ с помощью Буфера обмена (Clipboard).
Если по рисунку, находящемуся в Mathcad-документе, дважды щелкнуть левой кнопкой
мыши (имеется в виду, что к рисунку необходимо подвести курсор манипулятора
мышь и дважды щелкнуть (быстро нажать) по левой кнопке – принятая в среде
Windows технология активизации объекта
на экране дисплея), то рисунок будет автоматически перенесен в среду PaintBrush
(в среду графического редактора-прародителя), где его можно доработать.
Инструменты ввода текстовых комментариев (они
отличаются от математических формул, как правило, типом и цветом шрифта)
имеются в среде самого пакета Mathcad. Но объемные текстовые вставки лучше
вводить в среде текстового процессора Word, например, где есть, в частности,
инструменты проверки русской орфографии и грамматики, а затем переносить в
среду Mathcad.
По умолчанию нажатие на клавиши клавиатуры
приводит к вводу математического выражения (имени переменной, названия функции
и т.д.). Если в этот момент нажать клавишу пробела, то данная цепочка символов
превратится в начало комментария: тип и цвет шрифта поменяются на те, которые
соответствуют текстовому комментарию, а не математическому выражению (на экране
дисплея комментарии прописаны синим, а математические выражения – черным).
В пункте 1 на рис. 2 в расчет вводятся национальные и кратные единицы измерения
физических величин, которые будут задействованы в расчете. Здесь речь идет о пользовательских единицах измерения,
дополняющих встроенные в среду Mathcad (см. табл. 1). Это опять же повышает «читабельность»
документа (сравните H=2.32×106×J или H=2320×кДж) и позволяет пользователю оперировать теми единицами, которые в
большей степени дают ему чувствовать «физику» процесса.
Можно параллельно выводить значения
переменных в разных единицах (паскали, бары, атмосферы физические, атмосферы
технические, джоули, калории, BTU ¾ «бэтэушки»), чтобы человеку,
читающему документ, оставить право выбора.
Кроме того, в пункте 1 на рис. 2 вводятся две
вспомогательные функции пользователя. Первая (с именем °С) переводит безразмерную
температуру, под которой пользователь понимает градусы Цельсия[2],
в размерные градусы Кельвина. Эта функция будет вызываться в виде перефиксного
оператора (Т:=560°С — аргумент (операнд), затем
имя (символ) оператора, а не Т:=°С(560) — имя функции, а затем
аргумент в скобках), что опять же повышает «читабельность» Mathcad-документа.
Вторая функция (с именем ИЛИ) позволяет в расчете оперировать булевой операцией
логическое сложение.
Суть решаемой задачи: необходимо рассчитать
термический кпд простейшего обратимого паротурбинного цикла (цикла Ренкина), у
которого известны параметры (температура и давление) острого пара (пара,
выходящего из котла и направляемого в
турбину) и давление в конденсаторе.
Низкотемпературная часть цикла, замыкающая его — конденсатор и питательный
насос.
Рис. 2. Расчет в среде Mathcad кпд цикла Ренкина
На T-S диаграмме пронумерованы четыре характерные точки, фиксирующие четыре процесса в замкнутом цикле:
· 1-2 — адиабатное расширение пара в турбине;
· 2-2’ — конденсация пара в конденсаторе;
· 2’-3 — работа питательного насоса, превращающего конденсат в питательную воду;
· 3-1 — превращение питательной воды в перегретый пар (ломаная линия с тремя участками: доведение питательной воды до точки кипения, парообразование и перегрев пара).
Расчет термического кпд цикла сводится к
рассмотрению баланса теплоты и работы, подводимой в цикл и отводимой из цикла
(удельной, отнесенной к килограмму рабочего тела):
· теплота, подводимая в цикле — q1;
· работа турбины — lт;
· работа питательного насоса — lн.
Исходными данными для расчета являются следующие
параметры цикла (см. пункт 2 на рис. 8):
· давление острого пара;
· температура острого пара;
· давление в конденсаторе.
Расчет кпд цикла ведется двумя способами:
·
в режиме суперкалькулятора
(пункты 2 и 3 на рис. 2);
·
в режиме программного
формирования функции пользователя, возвращающей кпд цикла (пункт 4 на рис.2).
Режим суперкалькулятора незаменим при отладке расчета (при «нащупывании» решения и при поиске в нем ошибок) и при подготовке его протокола к проверке (например, к оппонированию рецензентом). Значение введенной переменной или переменной, рассчитанной по заданной пользователем формуле, тут же выводится на экран дисплея и/или бумагу принтера с выбранной пользователем размерностью и точностью, дополняется при необходимости графиками.
При работе с традиционными языками программирования пользователь ЭВМ вынужден работать с двумя отдельными документами — с текстом программы и с протоколом ее прогонки.
Функции, возвращающие термодинамические параметры воды и водяного пара, вводятся в расчет кпд ссылкой (Reference — см. начало пункта 3 на рис. 2) на соответствующий Mathcad-документ. После ссылки на внешний документ (его фрагменты ¾ это рис. 1 и 3) в текущем документе (рис. 2) становятся доступны функции, возвращающие термодинамические свойства воды и водяного пара. Далее расчет ведется по рутинным формулам, задающим основные параметры цикла: степень сухости пара, выходящего из турбины (x2), удельную работу турбины (lT), удельную работу насоса (lн), теплоту, подводимую в цикле (q1), и, наконец, сам термический кпд цикла (ht).
В пункте 4 на рис. 2 программно формируется функция пользователя ht(Р1 ,Р2,T1), возвращающая значение кпд цикла Ренкина в зависимости от значений трех аргументов: исходное (Р1) и конечное (Р2) давление в турбине и температура острого пара (T1). В функцию ht встроено пользовательское сообщение об ошибке (оператор error): расчет подразумевает, что в конденсатор поступает влажный пар (допущение расчета). При формировании функции ht все промежуточные значения оператором „ ¬ „ заносятся в локальные переменные, область видимости которых ограничена самой программой-функцией. Вертикальные линии отмечают начала и концы соответствующих операторных блоков. Формулы в функцию ht перенесены из отлаженного Mathcad-документа на рис. 8.
Функция пользователя ht(Р1, Р2, T1) позволяет средствами Mathcad построить табличные (пункт 4.3 на рис. 2) и графические (пункт 4.4) зависимости, связывающие кпд цикла Ренкина с его параметрами.
Пример 3. Оптимизация ступенчатого испарения в барабанном котле
В среде Mathcad допустимо решать задачи не только численными, но и аналитическими средствами, что будет проиллюстрировано следующим примером.
На рис. 3 представлен протокол решения задачи об оптимальном парораспределении в барабане котла со ступенчатым испарением с привлечением средств символьной математики Mathcad. Схема ступенчатого испарения, помещенная в начале рис. 3, поясняет суть этого способа повышения качества пара. Барабан котла разделяется на отсеки (как правило, третий отсек выполняют в виде выносного сепаратора), каждый из которых генерирует определенное количество влажного пара (пар затем поступает в пароперегреватель, а оттуда в турбину — см. схему цикла на рис. 2). Питательная вода (ее расход равен паропроизводительности плюс продувке) поступает в первый («чистый» отсек), где генерируется x паропроизводительности котла. Продувка первого отсека, является питательной водой второго (среднего) отсека, где генерируется y паропроизводительности. Третий «грязный» отсек генерирует остаток паропроизводительности (1-x-y). За счет такой технологии достигается существенное снижение концентрации загрязняющих примесей во влажном паре, выходящем из барабана котла (ступенчатое испарение называют «подарком котельщиков плохим химикам»): под качеством пара здесь подразумевают содержание загрязняющих примесей в нем. Примеси из кипящей воды переходят во влажный пар за счет двух процессов:
· капельный унос влаги;
· растворимость примеси в насыщенном водяном паре.
В расчете оба этих процесса будут учитываться через суммарный коэффициент выноса примеси K, равный отношению концентрации примеси во влажном паре к концентрации примеси в кипящей (котловой) воде.
Необходимо определить доли пара, генерируемые в первом (переменная x) и втором (y) отсеках, при которых концентрация примеси во влажном паре, выходящем из котла, была бы минимальна.
Рис. 3. Оптимизация ступенчатого испарения в среде Mathcad средствами символьной математики
Исходные данные расчета (пункт 2 на рис. 3): величина продувки из котла (переменная Pr), суммарные коэффициенты выноса примеси по отсекам — K1, К2 и К3 и концентрация примеси в питательной воде (Cw — формальный параметр, не влияющий на результат, но участвующий в промежуточных численных выкладках).
Ключевое место расчета — аналитическое формирование функции Cs(x, y), возвращающей концентрацию пара в зависимости от парораспределения в отсеках (конец пункта 3).
Формируется функция Cs(x, y) с помощью оператора символьных преобразований: ■ ■ ®, где первый операнд — это преобразуемое выражение, а второй — ключевое слово, задающее направление преобразования (решение уравнения или системы как на рис. 3 в пункте 3, упрощение выражения, раскрытие скобок, факторизация, взятие производных и интегралов и т.д.). Данные операторы вводятся через нажатие соответствующих кнопок панели символьных преобразований.
В задаче на рис. 3 в пункте 3 аналитически решаются относительно отмеченной переменной (параметр ключевого слова solve) составленные пользователем уравнения материального баланса примеси по отсекам: поступающая в отсек примесь (произведение концентрации на расход питательной воды) частично уносится с паром (с каплями влаги и через растворимость), остальная часть продувается в соседний отсек или совсем из барабана котла. Возможное отложение примеси на внутренних поверхностях котла, равно как и вымывание примеси с поверхностей котла в расчете не учитывается. Решения переносятся пользователем в оператор задания функции Сw1(x) := ■. Так формируются три функции с именами Сwi, где i — номер отсека. После этого по уравнению материального баланса составляется целевая функция Cs(x, y).
Поиск минимума функции Cs(x, y) предваряется ее графическим анализом (пункт 4): график линий уровня показывает, что в районе x ~ 0.9 и y ~ 0.1 находится минимум, который
уточняется в пункте 5 с использованием встроенной функции Minimize, возвращающей
численное решение задачи.
Авторы надеются, что читатель уяснил
преимущества работы в среде Mathcad при проведении
технологических и прочих расчетов.
Где можно приобрести пакет Mathcad?
Во-первых, можно «скачать» с сайта MathSoft (www.mathsoft.com) или с
сайта ее российского представителя (фирма СофтЛфйн ¾ www.softline.ru) бесплатную
и легальную read-only версию
пакета Mathcad ¾
пакет Mathcad Explorer.
Он позволяет полноценно работать с Mathcad-документами с одним исключением ¾
модифицированные документы нельзя записывать на диск. Mathcad Explorer позволяет, в частности,
считывать в сети Internet файлы своих коллег и использовать их для инженерной или
научно-педагогической деятельности. Во-вторых, полную коммерческую версию Mathcad
(включая и русскоязычную версию) можно приобрести у вышеупомянутого российского
представителя фирмы-разработчика – тел. (095) 932-00-23.
Пакет Mathcad представляет своим пользователям уникальную возможность общения через Internet. На сайте сервера фирмы MathSoft, Inc. под названием Collaboratory (Сотрудничество) есть такие разделы: математика и статистика, астрономия и навигация, электротехника, физика, химия и химическая технология и т.д. Через колонку Post… любой пользователь Mathcad или Mathcad Explorer может поместить на интересующей его странице решение конкретной задачи или сформулировать проблему. Другой пользователь через кнопку Post Reply… может вступить в дискуссию по данному вопросу. Так возникает и развивается телеконференция (форум) по той или иной научно-технической проблеме.
Выйти на сайт Collaboratory можно непосредственно из
среды Mathcad через Центр Ресурсов, где также хранится обширная справочная
информация: физические константы, таблица Менделеева, математические формулы и
многое другое.
О свойствах воды и водяного пара (и некоторых
других веществ) можно узнать, просмотрев в Internet следующие сайты:
·
http://www.iapws.org (Международная ассоциация
по свойствам воды и водяного пара);
·
http://webbook.nist.gov/chemistry/fluid
(Национальный институт стандартов США).
Литература:
1.
Очков
В.Ф. Mathcad 8 Pro для студентов и инженеров. — М.: КомпьютерПресс, 1999
2.
А.А.
Александров, Б.А. Григорьев. Таблицы теплофизических свойств воды и водяного
пара. М. Издательство МЭИ. 1999
3.
Theory and
Selected Problems of Thermodynamics for Engineers (Теория и
некоторые задачи курса термодинамики для инженеров). Электронный учебник для среды
Mathcad, созданный по одноименной книге Merle C. Potter и Craig W. Somerton.
Mathcad-файлы с решением рассмотренных
в данной статье проблем читатель может «скачать» по адресу ftp://twt.mpei.ac.ru/ochkov/thermo.mcd.
Там же помещены следующие папки:
· TOT – задачи тепло- и массообмена, представленные А.П. Солодовым;
· TOE – задачи теоретических основ электротехники (Э.В. Кузнецов);
· ASU – задачи из области автоматизированных систем управления (М.А. Панько, В.Р. Сабанин, В.В. Усенко, К.А. Орлов и др.)
· CHEM – задачи из области химико-технологических основ энергетики (В.Ф. Очков).
Богатая коллекция задач, решенных в среде Mathcad, ранится по Internet-адресу: http://www.mathsoft.com/appsindex.html.

